WebGL 绘制圆点
前言
这篇文章不说WebGL相关概念了,初学者先到网上看看WebGL相关概念。这里着重写一下在vue3前端框架下,如何通过webGL绘制圆点。
着色器代码(画点)
画点相关的着色器代码有顶点着色器和片元着色器,代码如下:
顶点着色器:
const vertexShaderSrc = `void main() {gl_Position = vec4(0, 0, 0, 1.0);gl_PointSize = 20.0;}
`;片元着色器:
const fragmentShaderSrc = `void main() {gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);}
`;初始化着色器
在网上找的一个通用的初始化着色器代码,如下所示:
function loadShader(gl, type, source) {//根据着色类型,建立着色器对象const shader = gl.createShader(type);//将着色器源文件传入着色器对象中gl.shaderSource(shader, source);//编译着色器对象gl.compileShader(shader);//返回着色器对象return shader;
}
export function initShaders(gl, vsSource, fsSource) {//创建程序对象const program = gl.createProgram();//建立着色对象const vertexShader = loadShader(gl, gl.VERTEX_SHADER, vsSource);const fragmentShader = loadShader(gl, gl.FRAGMENT_SHADER, fsSource);//把顶点着色对象装进程序对象中gl.attachShader(program, vertexShader);//把片元着色对象装进程序对象中gl.attachShader(program, fragmentShader);//连接webgl上下文对象和程序对象gl.linkProgram(program);//启动程序对象gl.useProgram(program);//将程序对象挂到上下文对象上gl.program = program;
}
代码中注释蛮详细的。
vue3框架使用webGL画点
这里直接贴上全部代码了,如下所示:
<template><div class="point-wrapper"><div style="margin-bottom: 20px">绘制点</div><canvas id="point" width="100" height="100"></canvas></div>
</template><script>
export default {name: "point",
};
</script><script setup>
import { onMounted } from "vue";
import { initShaders } from "@/utils/myGL.js";const vertexShaderSrc = `
void main() {gl_Position = vec4(0, 0, 0, 1.0);gl_PointSize = 20.0;
}
`;const fragmentShaderSrc = `
void main() {gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);
}
`;const fragmentShaderSrcCircle = `
precision mediump float;
void main() {float d = distance(gl_PointCoord, vec2(0.5, 0.5));if(d < 0.5) {gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);} else { discard; }
}
`;onMounted(() => {const canvas = document.getElementById("point");// webgl画笔const gl = canvas.getContext("webgl");// 初始化着色器initShaders(gl, vertexShaderSrc, fragmentShaderSrc);// 指定将要用来清理绘图区的颜色gl.clearColor(0.0, 0.0, 0.0, 1.0);// 清理绘图区gl.clear(gl.COLOR_BUFFER_BIT);// 绘制顶点gl.drawArrays(gl.POINTS, 0, 1);setTimeout(() => {initShaders(gl, vertexShaderSrc, fragmentShaderSrcCircle);// 指定将要用来清理绘图区的颜色gl.clearColor(0.0, 0.0, 0.0, 1.0);// 清理绘图区gl.clear(gl.COLOR_BUFFER_BIT);// 绘制顶点gl.drawArrays(gl.POINTS, 0, 1);}, 5000);
});
</script><style lang="scss" scoped>
.point-wrapper {width: 200px;height: 200px;background-color: gray;
}
</style>myGL.js中放的是初始化着色器initShaders 接口。
大家可以拷贝代码运行一下,刚开始出现一个正方形点,5秒后变成圆点
相关文章:

WebGL 绘制圆点
前言 这篇文章不说WebGL相关概念了,初学者先到网上看看WebGL相关概念。这里着重写一下在vue3前端框架下,如何通过webGL绘制圆点。 着色器代码(画点) 画点相关的着色器代码有顶点着色器和片元着色器,代码如下: 顶点着色器&…...

迅为RK3588开发板Android12 设置系统默认不锁屏
修改 frameworks/base/packages/SettingsProvider/res/values/defaults.xml 文件,修改为如下 所示: - <bool name"def_lockscreen_disabled">false</bool> <bool name"def_lockscreen_disabled">true</bool&…...

香港服务器速度快的原因
1. 传统域名解析过程 了解CDN系统先从域名解析说起。通常,我们在浏览器中输入域名,敲回车后,进入网站进行信息的获取。您分析过输入域名后浏览是如何请求到服务器上的信息,您了解域名解析的过程么? 1.1. 主机解析域…...

过滤器,监听器与拦截器的区别
过滤器,监听器与拦截器的区别 过滤器和监听器不是Spring MVC中的组件,而是Servlet的组件,由Servlet容器来管理。拦截器是Spring MVC中的组件,由Spring容器来管理 Servlet过滤器与Spring MVC 拦截器在Web应用中所处的层次如…...

clickhouse ssb-dbgen数据构造 及 clickhouse-benchmark简单压测
一、 测试数据构造 1. 数据样例 官方文档有给出一批数据样例。优点是比较真实,缺点是太大了,动辄上百G不适合简单小测试 Anonymized Yandex.Metrica DatasetStar Schema BenchmarkWikiStatTerabyte of Click Logs from CriteoAMPLab Big Data Benchma…...
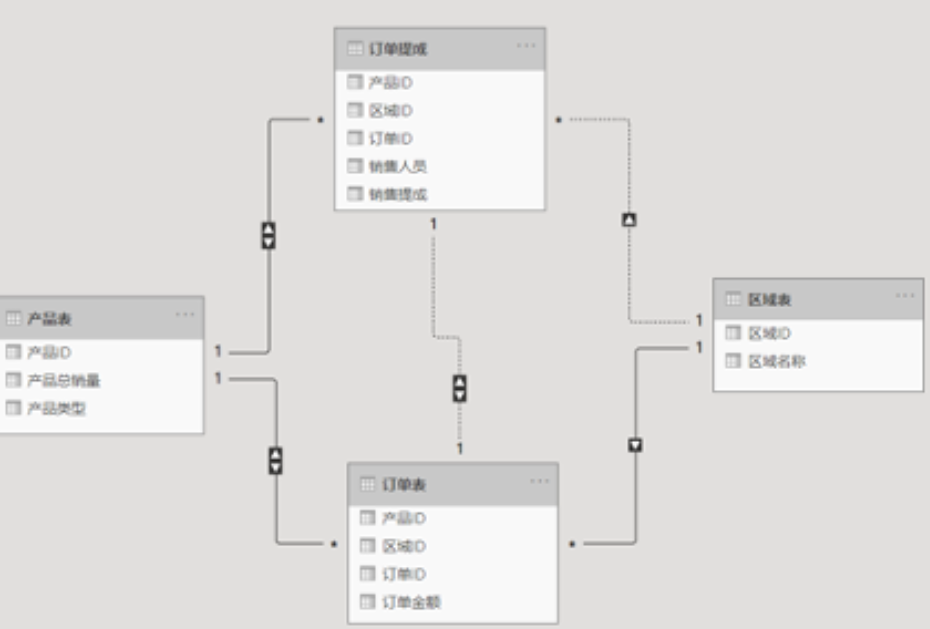
【数据分析】统计量
1. 均值、众数描述数据的集中趋势度量,四分位差、极差描述数据的离散程度。 2. 标准差、四分位差、异众比率度量离散程度,协方差是度量相关性。 期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为: 从直观上来看&…...

【通用消息通知服务】0x4 - 目前进展 阶段复盘
【通用消息通知服务】0x4 - 阶段复盘 达成 基本的API已经写完✍️了(消息查看发送, 模板crud,终端crud,发送渠道crud,计划crud,计划执行查看)拆分server, executor, planner三个入口, 方便针对性水平扩展整体架构初步形成,通过队列实现了事件驱动模型和消息订阅发…...
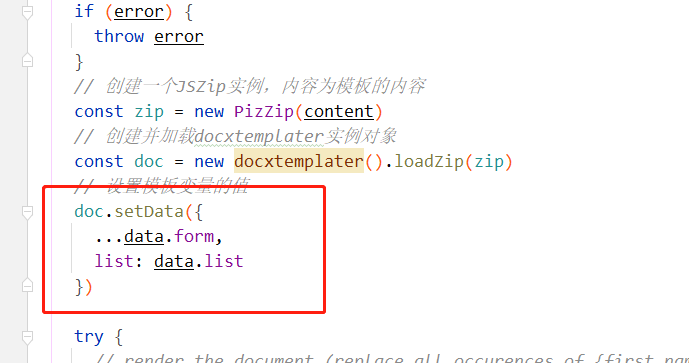
vue若依导出word文件,简单的实现
首先前端导包,注意exportDocx的导包位置要修改成你自己的 import {exportDocx} from /utils/docUtil/docutil.js; import {addDays} from date-fns; import {listGongyi} from "/api/system/detail";然后新建一个测试按钮 <el-col :span"1.5"><…...
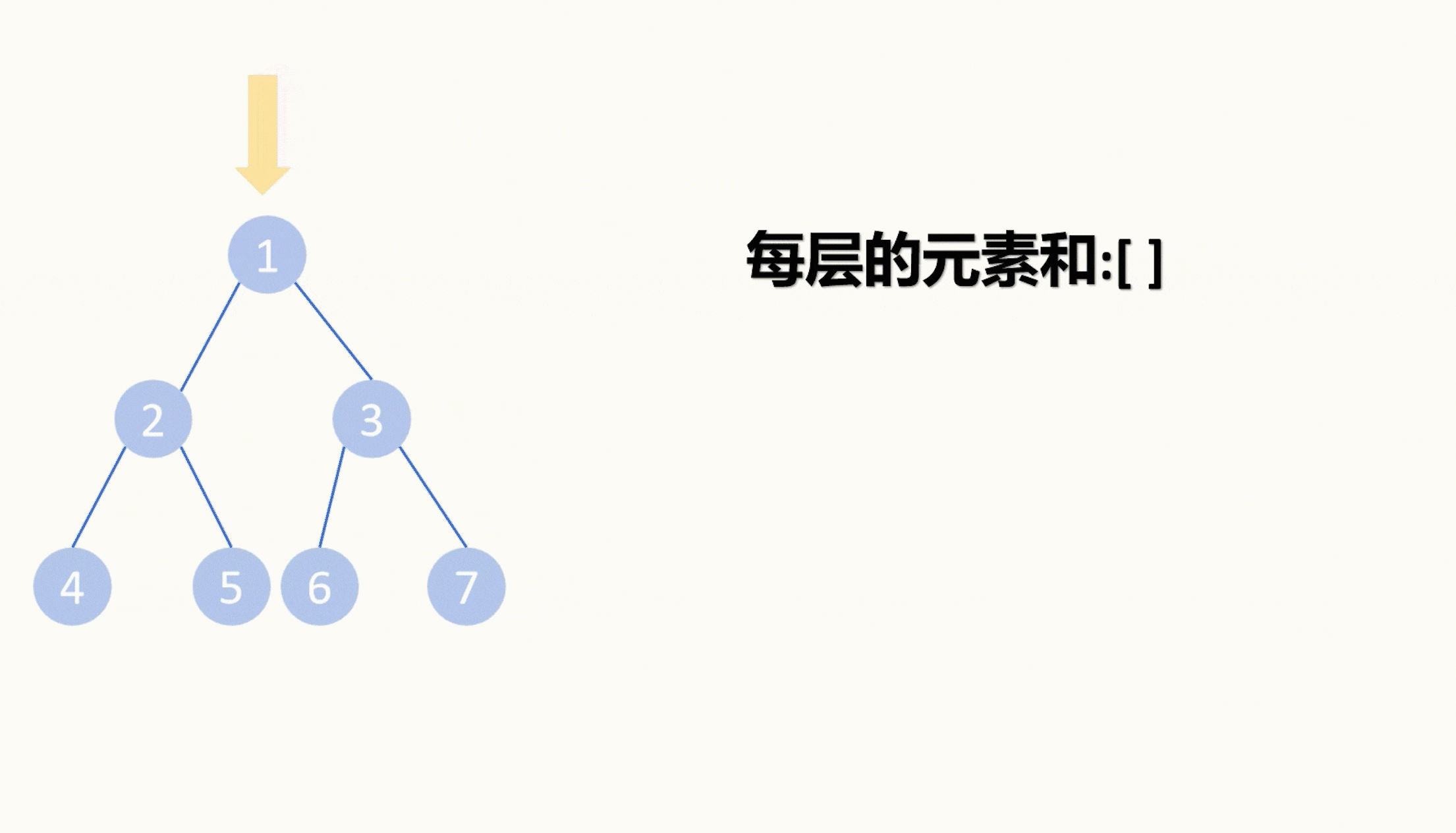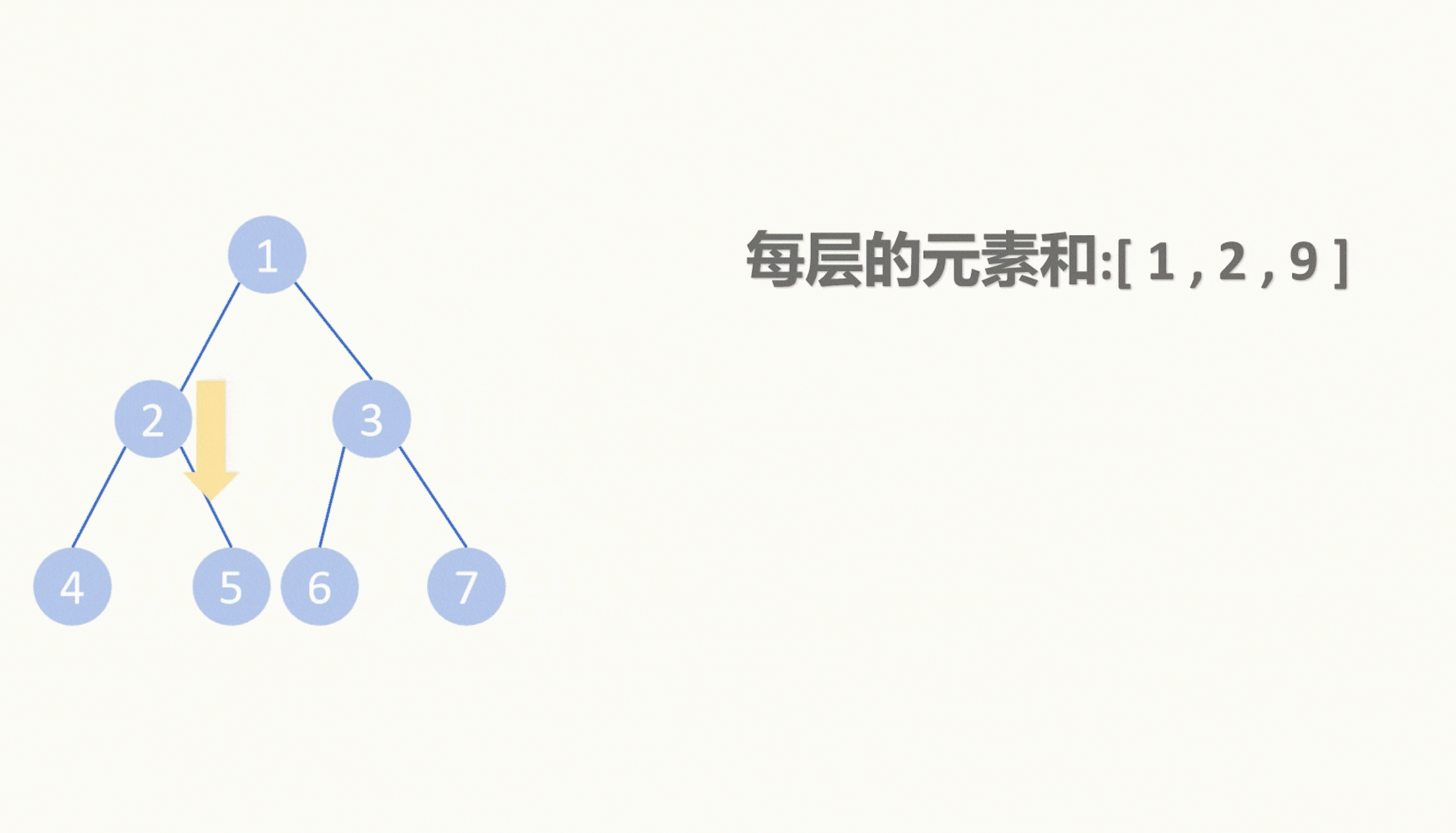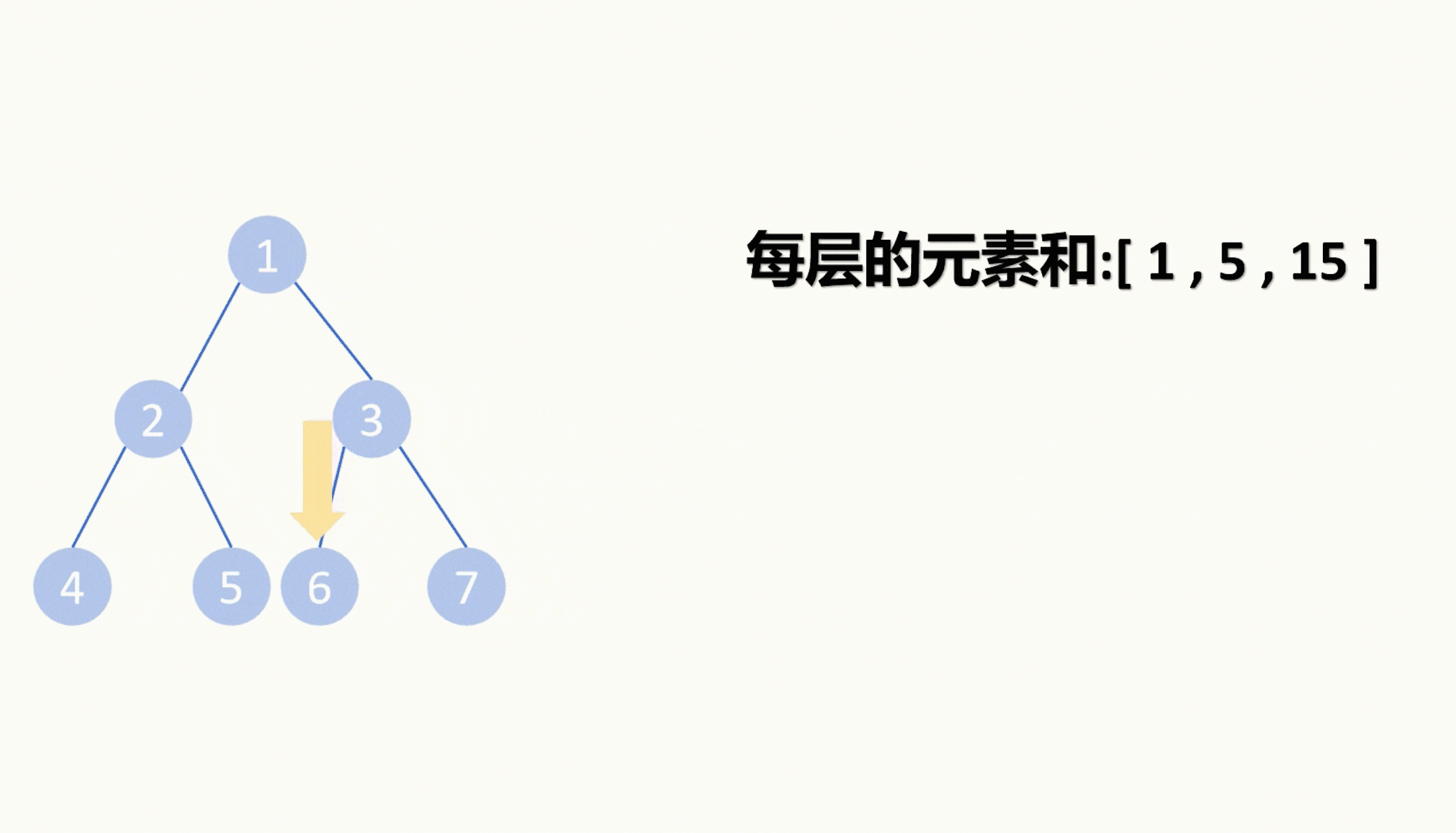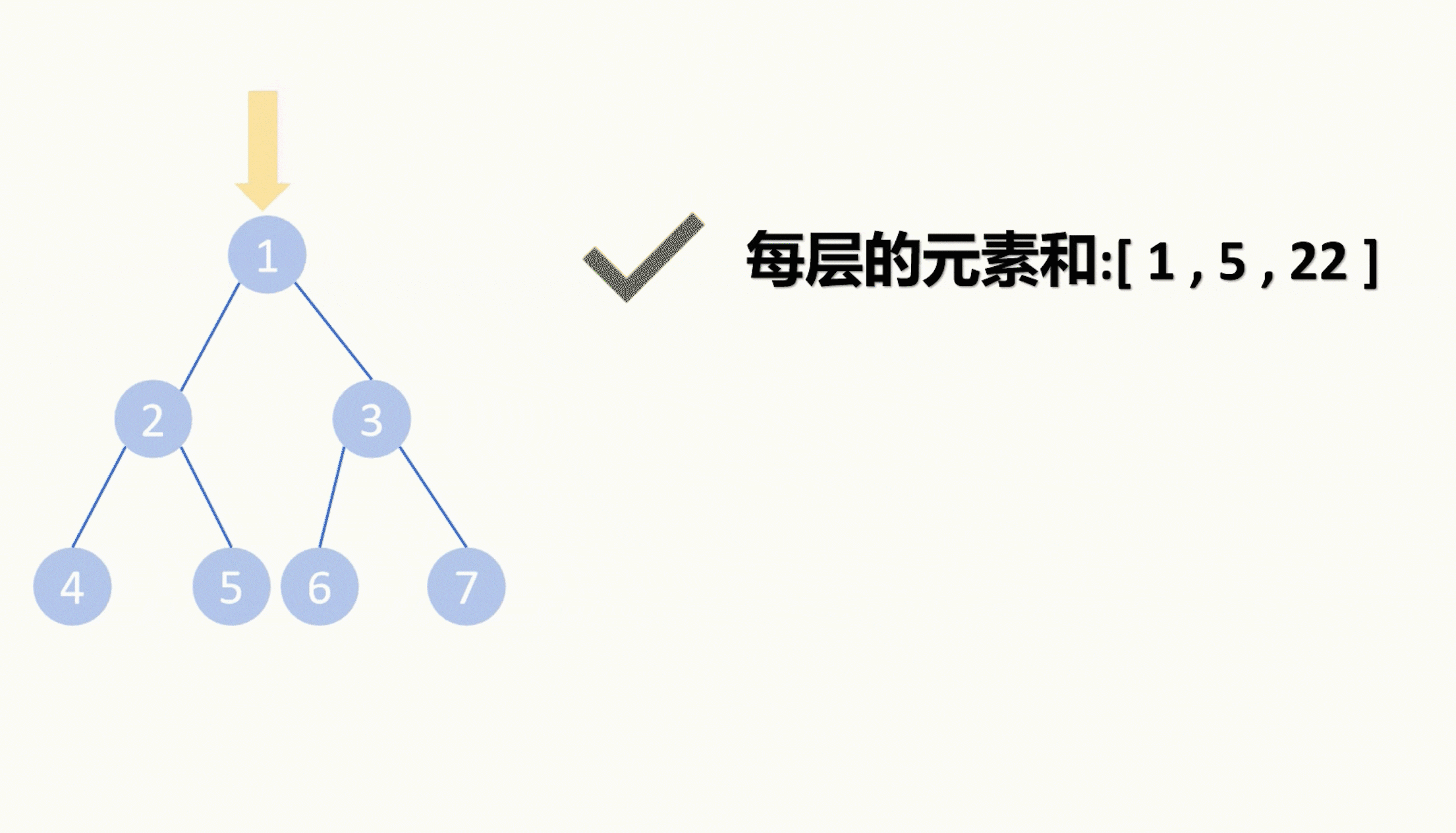
【LeetCode75】第四十题 最大层内元素和
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题和LeetCode75的上一题大同小异,都是要我们对二叉树进行层序遍历。 那具体如何层序遍历我再上一题也详细介绍过了&#…...

脱离束缚:数字化工厂中ARM控制器的革命性应用!
近年来,中国数字经济体系已进入高速增长阶段。制造业作为中国经济高质量发展的重要支撑力量,在面临生产成本不断上涨、关键装备和核心零部件“受制于人”等挑战时,建设数字化工厂已成必然。 数字化工厂数据采集出现的问题 在数字工厂的建设…...
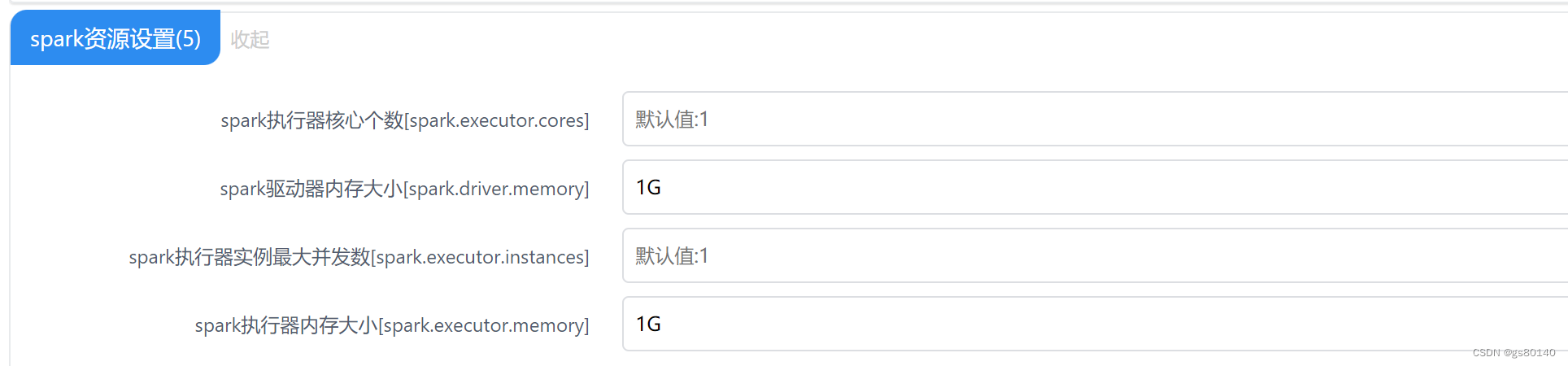
queue ide is not exists in YARN
报错内容: 2023-08-17 17:30:31.342 [ERROR] [BaseTaskScheduler-Thread-7 ] o.a.l.o.s.a.AsyncExecTaskRunnerImpl (79) [run] - Failed to execute task astJob_1_codeExec_1 org.apache.linkis.orchestrator.ecm.exception.ECMPluginErrorException: errCode:…...

【C++】UDP通信:客户端向服务端发送消息并接收服务端回应的消息
目录 1 UDP简介 2 通信 3 实践 4 运行结果 1 UDP简介 (1)UDP通信是无连接的,因此不需要connect操作。 (2)UDP通信过程需要指定数据接收端的IP和端口。 (3)UDP不对收到的数据进行排序。 (4)UDP对接收到的数据报不回复确认信息。 (5)如果发生了数据丢失,不会丢一…...
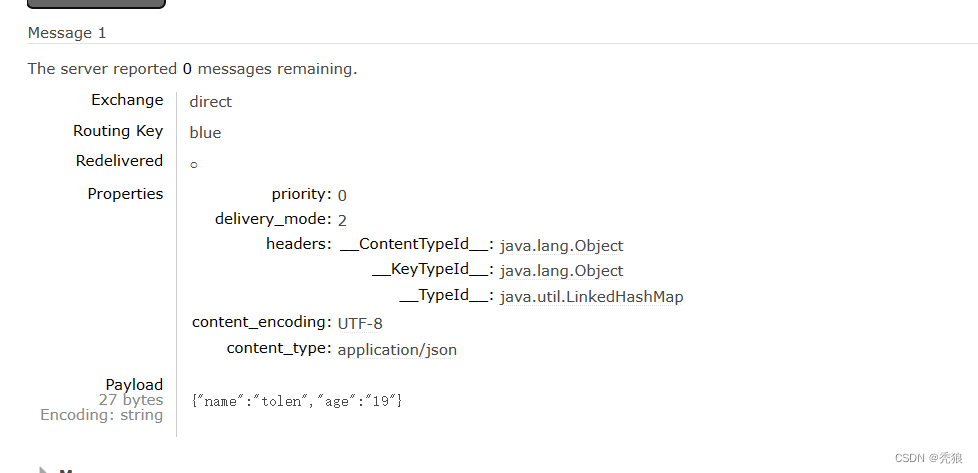
RabbitMq深度学习
什么是RabbitMq? RabbitMQ是一个开源的消息队列中间件,它实现了高级消息队列协议(AMQP)。它被广泛用于分布式系统中的消息传递和异步通信。RabbitMQ提供了一种可靠的、可扩展的机制来传递消息,使不同的应用程序能够相互之间进行…...
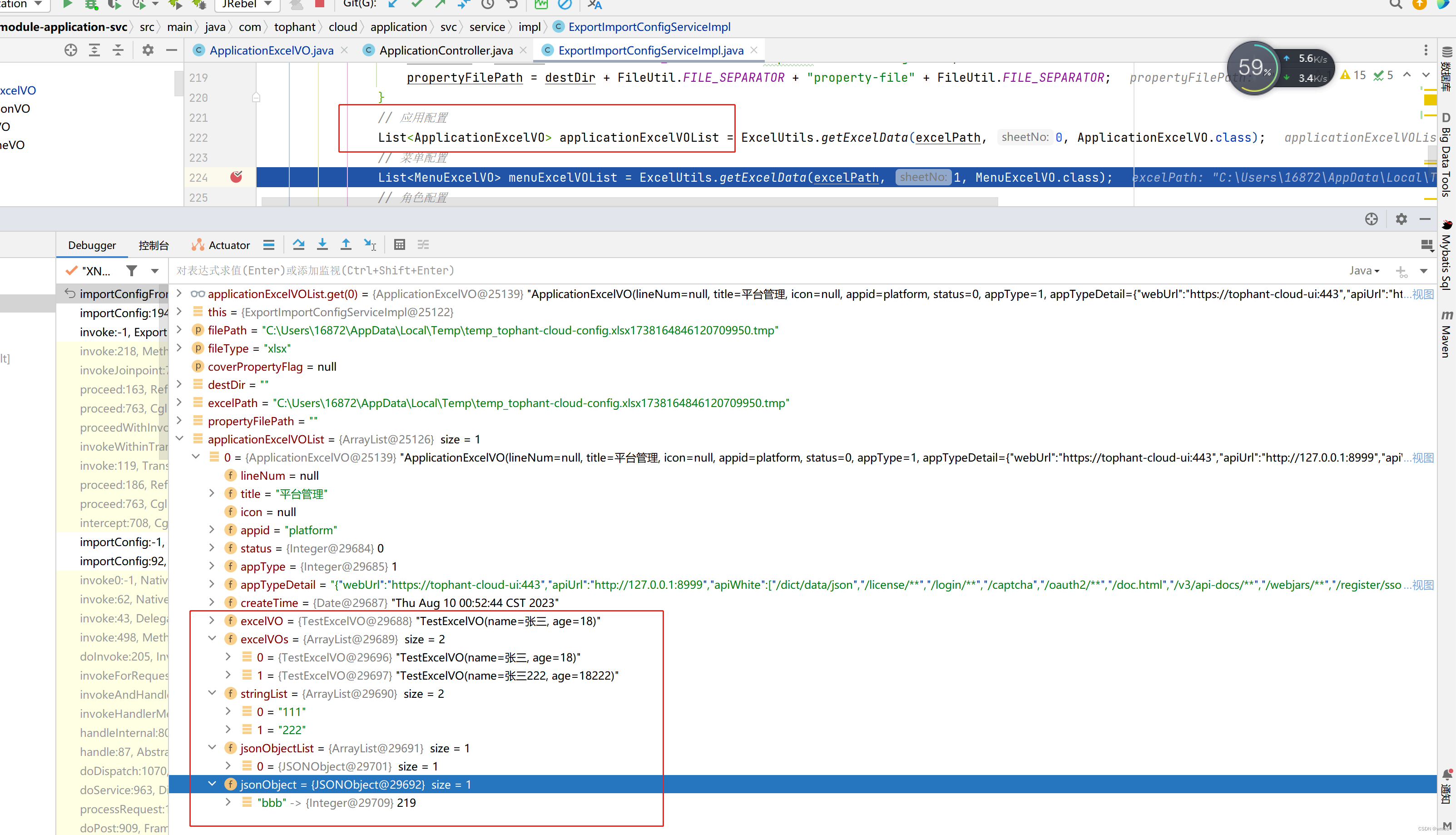
EasyExcel自定义字段对象转换器支持转换实体和集合实体
文章目录 1. 实现ObjectConverter2. 使用3. 测试3.1 导出excel3.2 导入excel 1. 实现ObjectConverter package com.tophant.cloud.common.excel.converters;import cn.hutool.json.JSONUtil; import com.alibaba.excel.converters.Converter; import com.alibaba.excel.enums.…...
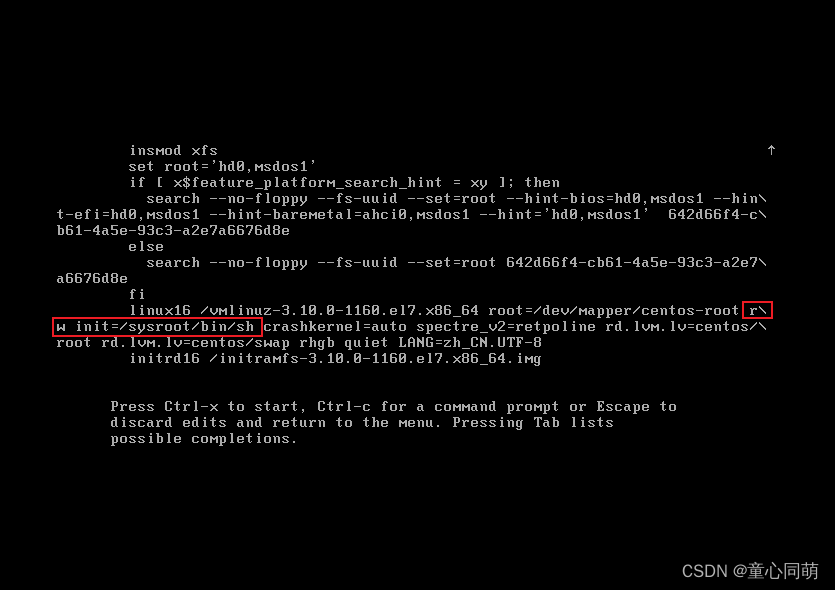
Linux重置ROOT密码(CentOS)
解释说明 在CentOS中重置root密码通常需要进入单用户模式,这是一个没有密码限制的特殊模式,允许您以root权限登录系统并更改密码。 重启系统 如果您无法登录到系统,可以通过重启系统来开始这个过程。您可以使用虚拟机控制台、物理服务器控制台…...

【Spring】一文带你彻底搞懂IOC、AOP
目录 首先简单了解一下什么是spring框架 什么是IOC? 什么是依赖注入(DI)? 控制反转和依赖注入又有什么关系? AOP是什么? SpringAOP的实现 说了这么多抽象概念,举个实例方便理解 首先简单…...
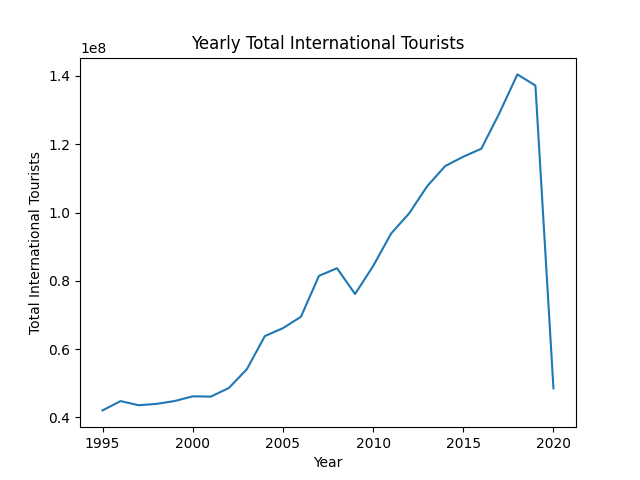
国际旅游网络的大数据分析(数学建模练习题)
题目:国际旅游网络的大数据分析 伴随着大数据时代的到来,数据分析已经深入到现代社会生活中的各个方面。 无论是国家政府部门、企事业单位还是个人,数据分析工作都是进行决策之前的 重要环节。 山东省应用统计学会是在省民政厅注册的学术类社会组织&…...

音视频技术开发周刊 | 308
每周一期,纵览音视频技术领域的干货。 新闻投稿:contributelivevideostack.com。 OpenAI首席科学家最新访谈:对模型创业两点建议、安全与对齐、Transformer够好吗? OpenAI首席科学家Ilya Sutskever最近和他的朋友Sven Strohband进…...

多旋翼飞控底层算法开发系列实验 | 多旋翼动力系统设计实验3
多旋翼动力系统设计实验3 01/多旋翼动力系统简介 多旋翼无人机的动力系统通常包括螺旋桨、电机、电调以及电池。动力系统是多旋翼最重要的组成部分,它决定了多旋翼的主要性能,如悬停时间、载重能力、飞行速度和飞行距离等。动力系统的部件…...
机制)
Redis之Sentinel(哨兵)机制
一、Sentinel是什么? Sentinel(哨岗、哨兵)是Redis的高可用性(high availability)解决方案:由一个或多个Sentinel实例(instance)组成的Sentinel系统(system)…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
