Java Math方法记录
Java 提供 java.lang.Math 类,很方便的进行数学运算。
Math 类是基于浮点数的运算,可能导致精度损失,不适用于高精度计算。
记录如下
常量
提供了两个常量,
Math.PI:圆周率πMath.E:自然对数的底数 e
System.out.println("圆周率 π : " + Math.PI);
System.out.println("自然对数的底数 e : " + Math.E);
圆周率 π : 3.141592653589793
自然对数的底数 e : 2.718281828459045
取值(最大值、最小值、绝对值、取反)
Math.max(int a, int b):取 a 、b 中的最大值。有重载方法,还支持 double 、float 、long 型参数。Math.min(int a, int b):取 a 、b 中的最小值。有重载方法,还支持 double 、float 、long 型参数。Math.abs(int a):取 a 的绝对值。有重载方法,还支持 double 、float 、long 型参数。Math.negateExact(int a):对 a 取反。有重载方法,还支持 long 型参数。
System.out.println("取最大值,示例 Math.max(100,200) : " + Math.max(100,200));
System.out.println("取最小值,示例 Math.min(100,200) : " + Math.min(100,200));
System.out.println("取绝对值,示例 Math.abs(-100) : " + Math.abs(-100));
System.out.println("取反,示例 Math.negateExact(100) : " + Math.negateExact(100));
取最大值,示例 Math.max(100,200) : 200
取最小值,示例 Math.min(100,200) : 100
取绝对值,示例 Math.abs(-100) : 100
取反,示例 Math.negateExact(100) : -100
四舍五入
Math.round(double a):对 a 四舍五入。有重载方法,还支持 float 型参数。
System.out.println("2023.4 四舍五入 : " + Math.round(2023.4));
System.out.println("2023.5 四舍五入 : " + Math.round(2023.5));
2023.4 四舍五入 : 2023
2023.5 四舍五入 : 2024
取整
Math.rint(double a): 返回最接近 a 的整数,如果有2个这样的整数,就返回其中的偶数。Math.ceil(double a):向上取整。Math.floor(double a):向下取整。
System.out.println("取最接近的整数 Math.rint(-2.5) : " + Math.rint(-2.1));System.out.println("取最接近的整数 Math.rint(-2.9) : " + Math.rint(-2.9));System.out.println("取最接近的整数 Math.rint(3.2) : " + Math.rint(3.2));System.out.println("取最接近的整数 Math.rint(4.7) : " + Math.rint(4.7));System.out.println("取最接近的整数 Math.rint(5.5) : " + Math.rint(5.5));System.out.println("99.5 向上取整 Math.ceil(99.5) : " + Math.ceil(99.5));System.out.println("99.5 向下取整 Math.floor(99.5) : " + Math.floor(99.5));System.out.println("-99.5 向上取整 Math.floor(-99.5) : " + Math.floor(-99.5));
取最接近的整数 Math.rint(-2.5) : -2.0
取最接近的整数 Math.rint(-2.9) : -3.0
取最接近的整数 Math.rint(3.2) : 3.0
取最接近的整数 Math.rint(4.7) : 5.0
取最接近的整数 Math.rint(5.5) : 6.0
99.5 向上取整 Math.ceil(99.5) : 100.0
99.5 向下取整 Math.floor(99.5) : 99.0
-99.5 向下取整 Math.floor(-99.5) : -100.0
加减乘除
Math.addExact(int x, int y):相加,有重载方法,还支持 long 型参数。Math.subtractExact(int x, int y):相减,返回 x - y 的值。有重载方法,还支持 long 型参数。Math.multiplyExact(int x, int y):相乘。有重载方法,还支持 long 型参数。Math.floorDiv(int x, int y):除法,返回 x / y 的值,返回值向下取整。即 查找小于或等于代数商的最大整数值。
System.out.println("加法,Math.addExact(4,5) : " + Math.addExact(4,5));System.out.println("减法,Math.subtractExact(10,7) : " + Math.subtractExact(10,7));System.out.println("乘法:Math.multiplyExact(3,7) : " + Math.multiplyExact(3,7));System.out.println("除法:Math.floorDiv(6,3) : " + Math.floorDiv(6,3));System.out.println("除法:Math.floorDiv(10L,3L) : " + Math.floorDiv(10L,3L));System.out.println("除法:Math.floorDiv(10,3) : " + Math.floorDiv(10,3));System.out.println("除法:Math.floorDiv(14L,5L) : " + Math.floorDiv(14L,5L));System.out.println("除法:Math.floorDiv(14,5) : " + Math.floorDiv(14,5));System.out.println("除法:14/5 : " + 14/5);System.out.println("除法:(float) 14/5 : " + (float)14/5);
加法,Math.addExact(4,5) : 9
减法,Math.subtractExact(10,7) : 3
乘法:Math.multiplyExact(3,7) : 21
除法:Math.floorDiv(6,3) : 2
除法:Math.floorDiv(10L,3L) : 3
除法:Math.floorDiv(10,3) : 3
除法:Math.floorDiv(14L,5L) : 2
除法:Math.floorDiv(14,5) : 2
除法:14/5 : 2
除法:(float) 14/5 : 2.8
取余
Math.IEEEremainder(double f1, double f2): 采用 IEEE 754 标准 ,f1 对 f2 取余 。
Math.IEEEremainder() 方法和 % 运算符返回的余数值等于 arg1-arg2 * n。但是, n 的值是不同的。
IEEEremainder() 方法 :n 是最接近 arg1/arg2 的整数,如果 arg1/arg2 返回一个介于两个整数之间的值,则 n 是偶数整数,即偶数取整。
% 运算符 :n 是 arg1/arg2 的整数部分,即向下取整。
举个例子,9 对 5 取余,
IEEEremainder() 方法 : n = 9/5 =1.8 ,取 2 。余数 = 9 - 5 * 2 = -1 。
% 运算符 :n = 9/5 = 1.8 , 取 1 。余数 = 9 - 5 * 1 = 4 。
System.out.println("求10/3的余数,采用IEEE 754标准,Math.IEEEremainder(9,5): " + Math.IEEEremainder(9,5));
System.out.println("求10/3的余数 9%5: " + 9%5);
求9/5的余数,采用IEEE 754标准,Math.IEEEremainder(9,5): -1.0
求9/5的余数 9%5: 4
取模
-
Math.floorMod(int x, int y):取模。有重载方法,还支持 long 型参数。返回值是 x - (floorDiv(x, y) * y) ,和除数 y 具有相同的符号 ,介于 -|y| < r < |y| 之间。
Math.floorMod() 方法 和 Math.floorDiv() 方法的关系是 : floorDiv(x, y) * y + floorMod(x, y) == x 。
Math.floorMod() 方法和 % 运算符的差异 :
如果 x 和 y 的符号相同,两者结果一致。
floorMod(4, 3) == 1; and (4 % 3) == 1
如果 x 和 y 的符号不相同,两者结果不一致。
floorMod(+4, -3) == -2; and (+4 % -3) == +1
floorMod(-4, +3) == +2; and (-4 % +3) == -1
floorMod(-4, -3) == -1; and (-4 % -3) == -1
随机数
Math.random():生成一个大于等于 0.0 且小于 1.0 的 double 型随机数。
System.out.println("生成一个随机数 Math.random() : " + Math.random());
生成一个随机数 Math.random() : 0.06326208314404602
幂次运算
Math.pow(double a, double b):求 a 的 b 次方。Math.exp(double a):求自然对数的底数 e 的 a 次方。
System.out.println("求2的3次方 Math.pow(2,3): " + Math.pow(2,3));
System.out.println("求自然对数的底数 e 的2次方 : " + Math.exp(2));
求2的3次方 Math.pow(2,3): 8.0
求自然对数的底数 e 的2次方 : 7.38905609893065
根号运算
Math.sqrt(double a):求 a 的平方根。Math.cbrt(double a):求 a 的立方根。
System.out.println("求25的平方根 Math.sqrt(25): " + Math.sqrt(25));
System.out.println("求27的立方根 Math.cbrt(27): " + Math.cbrt(27));
求25的平方根 Math.sqrt(25): 5.0
求27的立方根 Math.cbrt(27): 3.0
对数运算
Math.log(double a):求以 e 底 a 的对数。Math.log10(double a):求以 10 底 a 的对数。- 如果要计算以 a 为底 b 的对数,通过数学运算实现 :
Math.log(b)/Math.log(a)
System.out.println("求以e底e²的对数 Math.log(Math.E * Math.E) : " + Math.log(Math.E * Math.E));
System.out.println("求以10底100的对数 Math.log10(100) : " + Math.log10(100));
System.out.println("求以3为底81的对数 Math.log3(81) : " + Math.log(81)/Math.log(3));
求以e底e²的对数 Math.log(Math.E * Math.E) : 2.0
求以10底100的对数 Math.log10(100) : 2.0
求以3为底81的对数 Math.log3(81) : 4.0
弧度、角度运算
Math.toRadians(double angdeg): 把角度转换为弧度Math.toDegrees(double angrad):把弧度转换为角度
System.out.println("将角度转换为弧度 Math.toRadians(180) : " + Math.toRadians(180));//弧度 = 弧长 / 半径
System.out.println("将弧度转换为角度 Math.toRadians(3.14) : " + Math.toDegrees(3.14));
将角度转换为弧度 Math.toRadians(180) : 3.141592653589793
将弧度转换为角度 Math.toRadians(3.14) : 179.90874767107852
三角函数
Math.sin(double a):求角度的正弦函数值,非法输入则返回 NaNMath.asin(double a):求角度的余割函数值 (余割函数和正弦函数互为倒数),非法输入则返回 NaNMath.cos(double a):求角度的余弦函数值,非法输入则返回 NaNMath.acos(double a):求角度的正割函数值(正割函数和余弦函数互为倒数),非法输入则返回 NaNMath.tan(double a):求角度的正切函数值 ,非法输入则返回 NaNMath.atan(double a):求角度余切函数值 (余切函数和正切函数互为倒数),非法输入则返回 NaN
System.out.println("正弦 sin 90° ,Math.sin(90) : " + Math.sin(Math.toRadians(90)));
System.out.println("余割 csc 90° ,Math.asin(90) : " + Math.asin(Math.toRadians(90)));
System.out.println("余弦 cos 180° ,Math.cos(180) : " + Math.cos(Math.toRadians(180)));
System.out.println("正割 sec 180° ,Math.acos(180) : " + Math.acos(Math.toRadians(180)));
System.out.println("正切 tan 45° ,Math.tan(45) : " + Math.tan(Math.toRadians(45)));
System.out.println("余切 cot 45° ,Math.atan(45) : " + Math.atan(Math.toRadians(45)));
正弦 sin 90° ,Math.sin(90) : 1.0
余割 csc 90° ,Math.asin(90) : NaN
余弦 cos 180° ,Math.cos(180) : -1.0
正割 sec 180° ,Math.acos(180) : NaN
正切 tan 45° ,Math.tan(45) : 0.9999999999999999
余切 cot 45° ,Math.atan(45) : 0.6657737500283538
都知道 tan 45° = 1 ,输出的值是 0.9999999999999999 ,说明精度不准确。
相关文章:

Java Math方法记录
Java 提供 java.lang.Math 类,很方便的进行数学运算。 Math 类是基于浮点数的运算,可能导致精度损失,不适用于高精度计算。 记录如下 常量 提供了两个常量, Math.PI :圆周率πMath.E :自然对数的底数 …...
)
Java XPath 使用(2023/08/29)
Java XPath 使用(2023/08/29) 文章目录 Java XPath 使用(2023/08/29)1. 前言2. 技术选型3. 技术实现 1. 前言 众所周知,Java 语言适合应用于 Web 开发领域,不擅长用来编写爬虫。但在 Web 开发过程中有时又…...
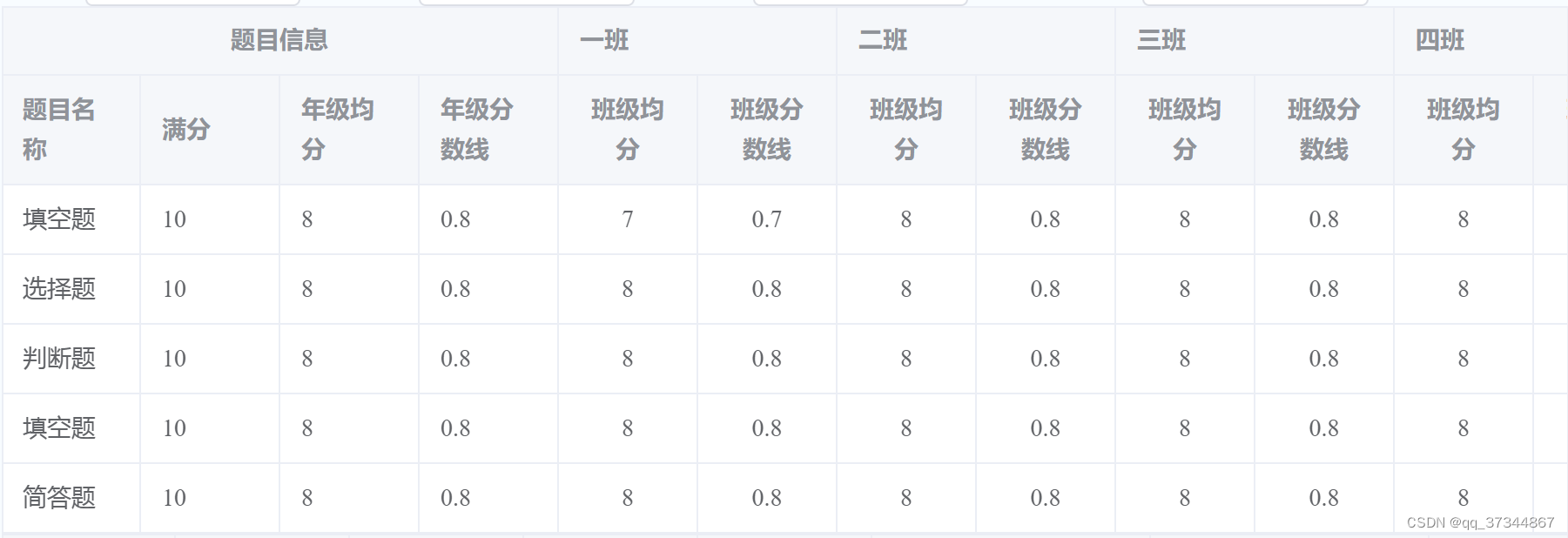
el-table动态生成多级表头的表格(js + ts)
展示形式: 详细代码: (js) <template><div><el-table :data"tableData" style"width: 100%"><el-table-column label"题目信息" align"center"><el-table-…...
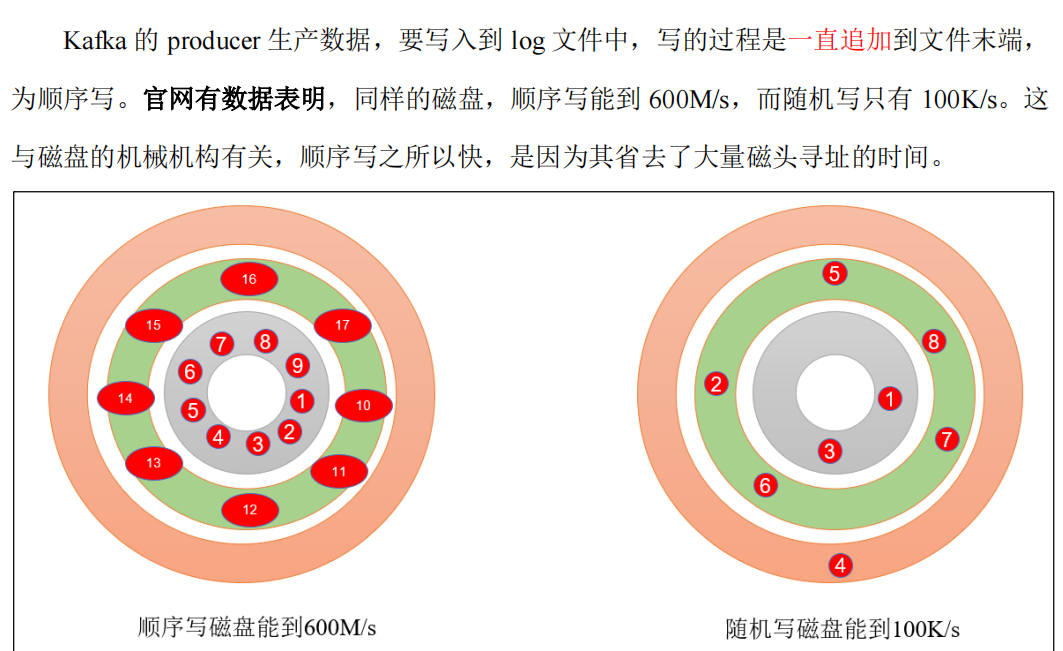
四、Kafka Broker
4.1.1 Zookeeper 存储的 Kafka 信息 4.1.2 Kafka Broker 总体工作流程 4.2 生产经验 - 节点的服役和退役 自己的理解:其实就是将kafka的分区,负载到集群中的各个节点上。 1、服役新节点 2、退役旧节点 4.3 kafka副本 1、副本的作用 2、Leader的选…...
ssm+vue医院医患管理系统源码和论文
ssmvue医院医患管理系统源码和论文077 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm vue.js 摘 要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已…...
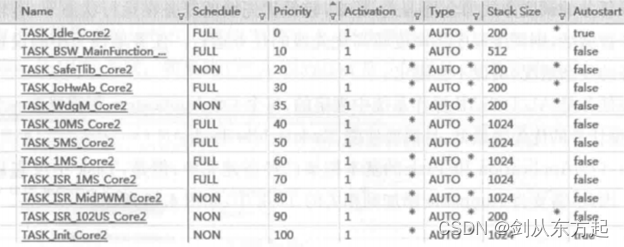
汽车电子笔记之:基于AUTOSAR的电机控制器架构设计
目录 1、概述 2、AUTOSAR设计 2.1、SWC设计 2.2、PORT设计 2.3、Runnable设计 2.4、电机控制器OS实现 1、概述 电机控制器应用层的软件架构较为复杂,主要包括PMSM(Permanent-MagnetSynchronous Motor)的矢量控制算法。根据PMSM的控制算法,对算法中的软件功能进行分析&…...

Docker 可以共享主机的参数
命令 docker run -it --ipchost nginx:latest /bin/bashdocker run -it --nethost nginx:latest /bin/bashdocker run -it --pidhost nginx:latest /bin/bashdocker run -it --utshost nginx:latest /bin/bash 参考 Docker run reference | Docker Docs...
)
STL之list模拟实现(反向迭代器讲解以及迭代器失效)
这次是关于list的模拟实现的代码,先看看下面的代码: #pragma once #include <iostream> #include "reve_iterator.hpp" using namespace std; namespace cc {//链表节点template<class T>struct ListNode{T _val;ListNode *_next…...

Firewalld防火墙新增端口、开启、查看等
Linux操作系统中,Firewalld防火墙相关操作如下: 安装 yum install firewalld firewalld-configFirewall开启常见端口命令 新增防火墙端口命令: firewall-cmd --zonepublic --add-port80/tcp --permanentfirewall-cmd --zonepublic --add-…...
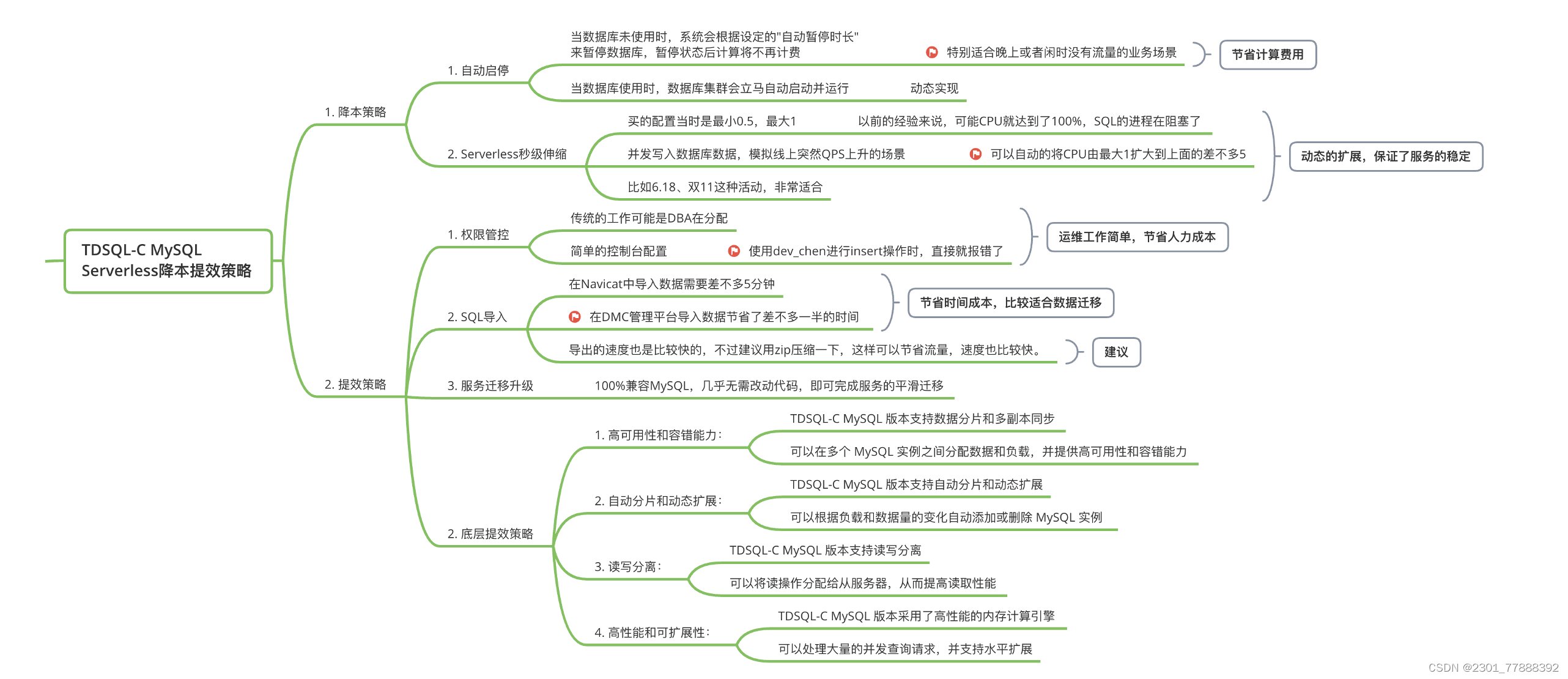
【腾讯云 TDSQL-C Serverless 产品测评】- 云原生时代的TDSQL-C MySQL数据库技术实践
一、活动介绍: “腾讯云 TDSQL-C 产品测评活动”是由腾讯云联合 CSDN 推出的针对数据库产品测评及产品体验活动,本次活动主要面向 TDSQL-C Serverless版本,初步的产品体验或针对TDSQL-C产品的自动弹性能力、自动启停能力、兼容性、安全、并发…...

计算机硬件基础
计算机硬件基础 教程:计算机硬件基础_哔哩哔哩_bilibili 一.计算机的分类 台式机、笔记本电脑、上网本、超薄笔记本、平板电脑、游戏本、智能手机、超级移动电脑、便携式电脑、车用电脑、工作站、服务器、工业电脑IPC、ECDIS 二.机箱 放硬件的地方、一般由钢和铝等…...

云计算和Docker分别适用场景
在大规模网络爬虫系统中,通过使用云计算和Docker技术,可以实现大规模网络爬虫系统的高效架构设计和部署。这种架构能够提供可扩展性、高可用性和灵活性,为爬虫系统的运行和管理带来便利。 云计算和Docker在大规模网络爬虫系统中有不同的业务…...
oracle 基础运用2
首先在电脑上安装PLSQL developer,这个是oracle图形化连接工具,然后安装win64_11gR2_client,这个是orace客户端,安装完成后可以在cmd命令行输入sqlplus命令进行验证,如图表示安装成功。 作为sys的连接应该是SySDBA或Sy…...

ThinkPHP 资源路由的简单使用,restfull风格API
ThinkPHP 资源路由的简单使用,restfull风格API 一、资源控制器二、资源控制器简单使用 一、资源控制器 资源控制器可以轻松的创建RESTFul资源控制器,可以通过命令行生成需要的资源控制器,例如生成index应用的TestR资源控制器使用:…...

利用前缀树获取最小目录
一、任务名: 开发最小目录工具 二、任务描述 开发工具,从桶清单文件中列举出所有最小目录,并列举出每一个最小目录中包含的文件总数与文件总量。 最小目录的解释: 有以下几个目录 a/b/1.txt a/b/2/txt a/3.txt a/b/c/ 则&…...

Java【手撕双指针】LeetCode 18. “四数之和“, 图文详解思路分析 + 代码
文章目录 前言一、四数之和1, 题目2, 思路分析3, 代码 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等 📗 Java数据结构: 顺序表, 链表, 堆…...

OpenCV处理图像和计算机视觉任务时常见的算法和功能
当涉及到OpenCV处理图像和计算机视觉任务时,有许多常见的具体算法和功能。以下是一些更具体的细分: 图像处理算法: 图像去噪:包括均值去噪、高斯去噪、中值滤波等,用于减少图像中的噪声。 直方图均衡化:用…...

Flutter实现StackView
1.让界面之间可以嵌套且执行动画。 2.界面的添加遵循先进后出原则。 3.需要使用AnimateView,请看我上一篇博客。 演示: 代码: Stack: import package:flutter/cupertino.dart;///栈,先进后出 class KqWidgetStack {final Lis…...

c++ future与promise
C11 标准中 头文件中包含了以下几个类和函数: Providers 类:std::promise, std::package_taskFutures 类:std::future, shared_future.Providers 函数:std::async()其他类型:std::future_error, std::future_errc, st…...

在x86机器上的Docker运行arm64容器
1. 引言 工作中常用电脑主机CPU为x86架构,有时由于产品需要,我们需要编译aarch64架构的SDK或者应用程序供使用或者测试。 一种比较快捷的方式是使用aarch64的CPU构建相应操作系统,实现真机运行。但在无arm架构CPU环境下,我们可否…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
