第三讲,实践编程 Eigen
目录
- 1.实践 Eigen
- 1.1 Eigen的简介
- 1.2 Eigen 向量和矩阵的 声明
- 1.3 Eigen的输出操作
- 1.4 矩阵和向量相乘 要注意数据类型 矩阵纬度
- 1.5 矩阵的四则运算
- 1.6 矩阵求解特征向量和特征值
- 1.7 解方程 求逆
1.实践 Eigen
1.1 Eigen的简介
Eigen是一个 C++ 开源线性代数库。它提供了快速的有关矩阵的线性代数运算,还包括解方程等功能。许多上层的软件库也使用 Eigen 进行矩阵运算,包括 g2o、Sophus 等。
相比于其他库,Eigen 特殊之处在于,它是一个纯用头文件搭建起来的库。这意味着你只能找到它的头文件,而没有.so 或.a 那样的二进制文件。 我们在使用时,只需引入 Eigen 的头文件即可,不需要链接它的库文件(因为它没有库文件)。
1.2 Eigen 向量和矩阵的 声明
// 声明一个2*3的float矩阵Eigen::Matrix<float, 2, 3> matrix_23;// 同时,Eigen 通过 typedef 提供了许多内置类型,不过底层仍是Eigen::Matrix// 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>,即三维向量Eigen::Vector3d v_3d;// 效果这是一样的Eigen::Matrix<float,3,1> vd_3d;// Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero(); //初始化为零// 如果不确定矩阵大小,可以使用动态大小的矩阵Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;// 还有更简单的Eigen::MatrixXd matrix_x;
1.3 Eigen的输出操作
// 声明一个2*3的float矩阵Eigen::Matrix<float, 2, 3> matrix_23; // 下面是对Eigen阵的操作// 输入数据(初始化)matrix_23 << 1, 2, 3, 4, 5, 6;// 输出cout << matrix_23 << endl;//输出结果 1 2 3// 4 5 6// 用()访问矩阵中的元素for (int i=0; i<2; i++) {for (int j=0; j<3; j++)cout<<matrix_23(i,j)<<"\t";cout<<endl;}//输出结果 1 2 3// 4 5 6//也可以跟数组访问一样matrix_23[0];//结果 1
1.4 矩阵和向量相乘 要注意数据类型 矩阵纬度
Eigen::Vector3d v_3d;//内置的是double类型Eigen::Matrix<float,3,1> vd_3d; Eigen::MatrixXd matrix_x;// 矩阵和向量相乘(实际上仍是矩阵和矩阵)matrix_23 << 1, 2, 3, 4, 5, 6;v_3d << 3, 2, 1;vd_3d << 4,5,6;// 但是在Eigen里你不能混合两种不同类型的矩阵,double类型的不能和float类型的相乘,像这样是错的// Eigen::Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;// 应该显式转换//matrix_23.cast<double>() matrix_23矩阵转变为double类型Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;cout << result << endl;Eigen::Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;cout << result2 << endl;// 同样你不能搞错矩阵的维度// 试着取消下面的注释,看看Eigen会报什么错// Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d;
1.5 矩阵的四则运算
matrix_33 = Eigen::Matrix3d::Random(); // 随机数矩阵cout << matrix_33 << endl << endl;cout << matrix_33.transpose() << endl; // 转置cout << matrix_33.sum() << endl; // 各元素和cout << matrix_33.trace() << endl; // 迹cout << 10*matrix_33 << endl; // 数乘cout << matrix_33.inverse() << endl; // 逆cout << matrix_33.determinant() << endl; // 行列式1.6 矩阵求解特征向量和特征值
// 特征值// 实对称矩阵可以保证对角化成功Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose()*matrix_33 );cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;//特征值cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;//特征向量
1.7 解方程 求逆
// 解方程// 我们求解 matrix_NN * x = v_Nd 这个方程// N的大小在前边的宏里定义,它由随机数生成// 直接求逆自然是最直接的,但是求逆运算量大Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );Eigen::Matrix< double, MATRIX_SIZE, 1> v_Nd;v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );clock_t time_stt = clock(); // 计时// 直接求逆Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;cout <<"time use in normal inverse is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;// 通常用矩阵分解来求,例如QR分解,速度会快很多time_stt = clock();x = matrix_NN.colPivHouseholderQr().solve(v_Nd);cout <<"time use in Qr decomposition is " <<1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;
相关文章:

第三讲,实践编程 Eigen
目录 1.实践 Eigen1.1 Eigen的简介1.2 Eigen 向量和矩阵的 声明1.3 Eigen的输出操作1.4 矩阵和向量相乘 要注意数据类型 矩阵纬度1.5 矩阵的四则运算1.6 矩阵求解特征向量和特征值1.7 解方程 求逆 1.实践 Eigen 1.1 Eigen的简介 Eigen是一个 C 开源线性代数库。它提供了快…...

POI实现百万数据导出
1、概述 我们都知道Excel可以分为早期的Excel2003版本(使用POI的HSSF对象操作)和Excel2007版本(使用POI的XSSF操作),两者对百万数据的支持如下: Excel 2003:在POI中使用HSSF对象时&#…...

如何制作党建专题汇报片
通过展示党组织的凝聚力和战斗力,增强党员的组织归属感和团结合作意识。通过宣传片,可以加强党组织的凝聚力,推动党的事业发展。制作党建专题汇报片需要一定的前期准备和后期制作技巧。下面是由深圳党建专题汇报片制作公司老友记小编为您整理…...

沉浸式VR虚拟实景样板间降低了看房购房的难度
720 全景是一种以全景视角为特点的虚拟现实展示方式,它通过全景图像和虚拟现实技术,将用户带入一个仿佛置身其中的沉浸式体验中。720 全景可以应用于旅游、房地产、展览等多个领域,为用户提供更为直观、真实的体验。 在房地产领域,…...

如何在Linux环境下给Web应用配置HTTPS证书
如何在Linux环境下给Web应用配置HTTPS证书 在当今互联网时代,保护用户数据的安全性至关重要。为你的Web应用启用HTTPS协议是确保数据传输加密和身份验证的一种有效方式。本文将指导你如何在Linux环境下为Web应用程序配置HTTPS证书。 1. 获取SSL证书 首先…...

面试题-React(七):React组件通信
在React开发中,组件通信是一个核心概念,它使得不同组件能够协同工作,实现更复杂的交互和数据传递。常见的组件通信方式:父传子和子传父 一、父传子通信方式 父组件向子组件传递数据是React中最常见的一种通信方式。这种方式适用…...
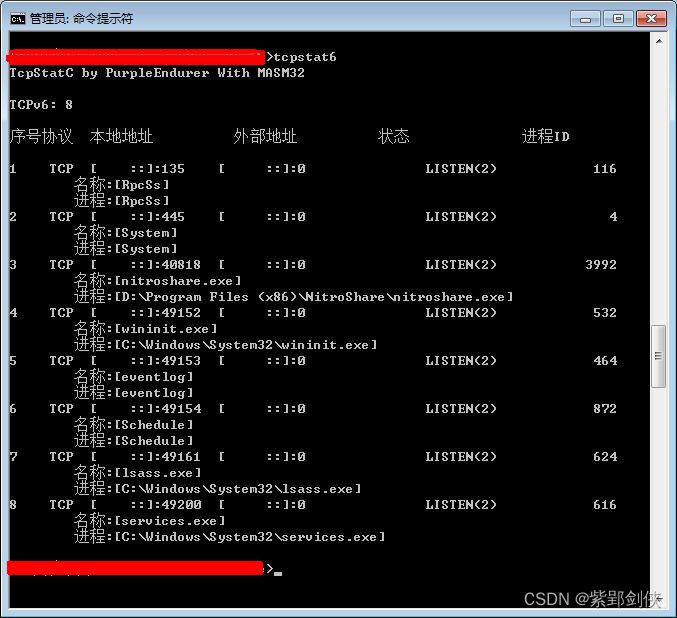
MASM32编程调用 API函数RtlIpv6AddressToString,Windows 10 容易,Windows 7 折腾
一、需求分析 最近用MASM32编程更新SysInfo,增加对IPv6连接信息的收集功能,其中涉及到 MIB_TCP6ROW_OWNER_MODULE 结构体: ;typedef struct _MIB_TCP6ROW_OWNER_MODULE { ; UCHAR ucLocalAddr[16]; ; DWORD dwLocalScope…...
为什么使用Nacos而不是Eureka(Nacos和Eureka的区别)
文章目录 前言一、Eureka是什么?二、Nacos是什么?三、Nacos和Eureka的区别3.1 支持的CAP3.2连接方式3.3 服务异常剔除3.4 操作实例方式 总结 前言 为什么如今微服务注册中心用Nacos相对比用Eureka的多了?本文章将介绍他们之间的区别和优缺点…...

Python作业一
目录 1、用循环语句求122333444455555的和 2、求出2000-2100的所有闰年,条件是四年一闰,百年不闰,四百年再闰 3、输入两个正整数,并求出它们的最大公约数和最小公倍数 4、求出100以内的所有质数 5、求100以内最大的10个质数的…...

protobuf概览
protobuf protobuf是由谷歌推出的二进制序列化与反序列化库对象。也是著名GRPC的底层依赖,它独立于平台及语言的序列化与反序列化标准库。 相关网址 protobuf IDL描述protobuf 开源库grpc-知乎grpc官方示例 安装protobuf可以使用vcpkg进行简易安装依赖ÿ…...
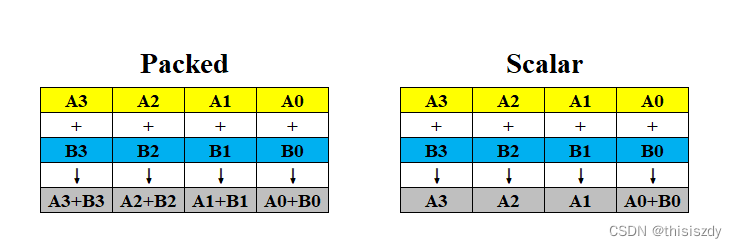
<C++> SSE指令集
SSE指令集 include库 #include <mmintrin.h> //MMX #include <xmmintrin.h> //SSE(include mmintrin.h) #include <emmintrin.h> //SSE2(include xmmintrin.h) #include <pmmintrin.h> //SSE3(include emmintrin.h) #include <tmmintrin.h> /…...
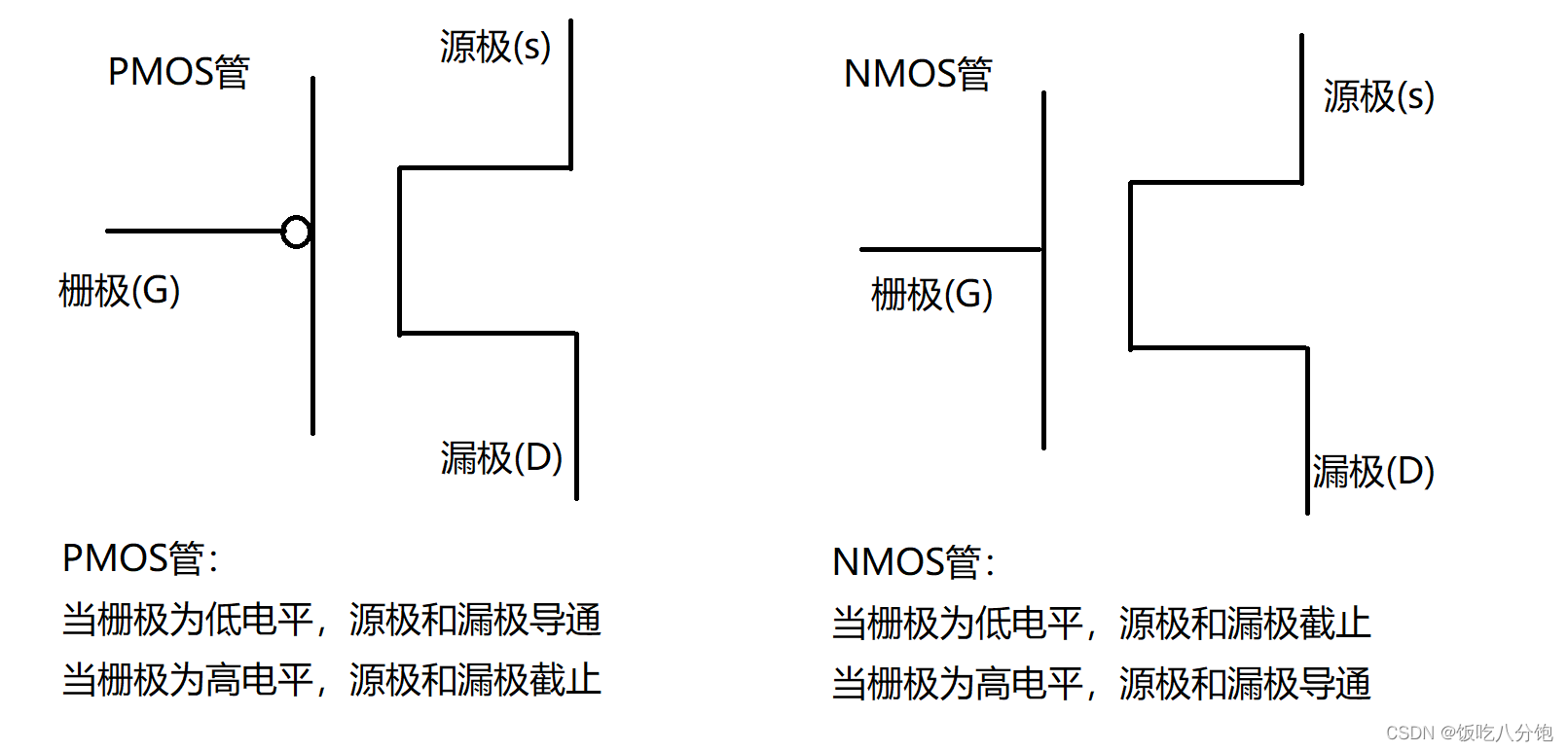
cortex-A7核LED灯实验--STM32MP157
实验目的:实现LED1 / LED2 / LED3三盏灯工作 一,分析电路图 1,思路 分析电路图可知: 网络编号 引脚编号 LED1 PE10 LED2 > PF10 LED3 > PE8 2,工作原理: 写1:LED灯亮…...
WPF实战项目十三(API篇):备忘录功能api接口、优化待办事项api接口
1、新建MenoDto.cs /// <summary>/// 备忘录传输实体/// </summary>public class MenoDto : BaseDto{private string title;/// <summary>/// 标题/// </summary>public string Title{get { return title; }set { title value; }}private string con…...
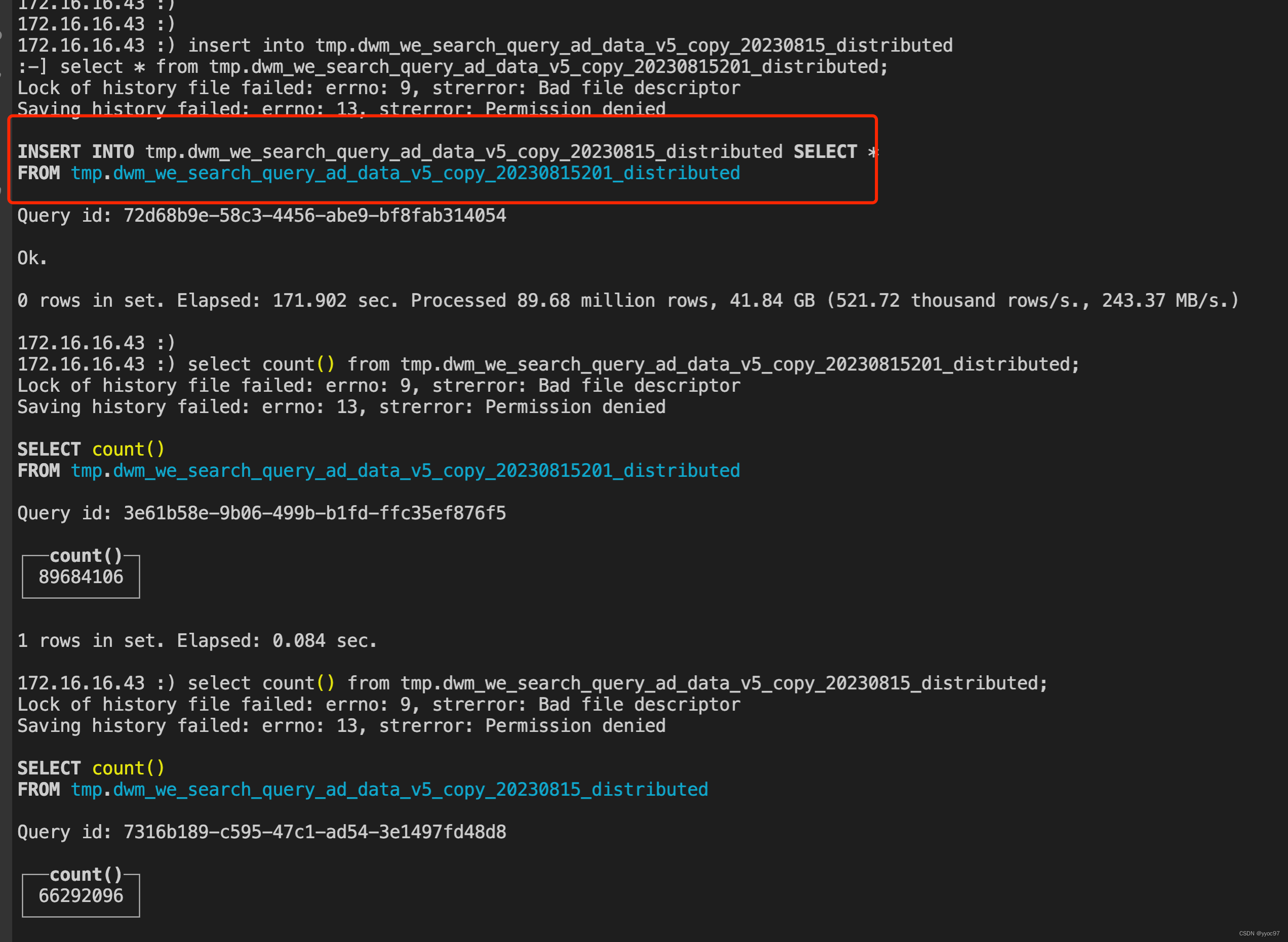
clickhouse(十四、分布式DDL阻塞及同步阻塞问题)
文章目录 一、分布式ddl 阻塞、超时现象验证方法解决方案 二、副本同步阻塞现象验证解决方案 一、分布式ddl 阻塞、超时 现象 在clickhouse 集群的操作中,如果同时执行一些重量级变更语句,往往会引起阻塞。 一般是由于节点堆积过多耗时的ddl。然后抛出…...

怎么入门网络安全(黑客)?
目录: 一、自学网络安全学习的误区和陷阱 1.不要试图先成为一名程序员(以编程为基础的学习)再开始学习2.不要把深度学习作为入门第一课3.以黑客技能、兴趣为方向的自学误区:4.不要收集过多的资料二、学习网络安全的一些前期准备三…...

c++ boost::json
Boost社区12月11日发布了1.75版本,在之前,Boost使用Boost.PropertyTree解析JSON,XML,INI和INFO格式的文件。但是由于成文较早及需要兼容其他的数据格式,相比较于其他的…...
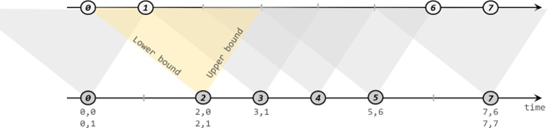
《Flink学习笔记》——第九章 多流转换
无论是基本的简单转换和聚合,还是基于窗口的计算,我们都是针对一条流上的数据进行处理的。而在实际应用中,可能需要将不同来源的数据连接合并在一起处理,也有可能需要将一条流拆分开,所以经常会有对多条流进行处理的场…...

openmmlab出现KeyError: ‘xxx is not in the model registry....‘
问题描述 在复现基于mmpose框架的算法时,运行程序出现KeyError: xxx is not in the model registry....的问题,报错原因是自定义的backbone等结构或者某些当前代码使用的方法没有注册到现有的包中, 导致在import的时候无法导入该方法。 解决方案 找到…...

错误代码0x80131500要怎么解决?快速修复方法
错误代码0x80131500通常与.NET Framework 相关的问题有关。它可能表示.NET Framework的安装损坏、版本冲突或系统文件缺失等。下面我们一起来探讨一下解决错误代码0x80131500有哪些。 以下是一些解决方法 安装最新的.NET Framework版本:访问Microsoft官方网站&…...
)
PMO(Project Management Office)
PMO 是项目管理办公室(Project Management Office)的缩写。它是组织内的一个部门或团队,负责支持和促进项目管理活动,以确保项目按时、按预算、按要求完成。 PMO 的职责和角色可以因组织的性质和需求而有所不同,但通常…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
