【期末复习】例题讲解Dijkstra算法
使用场景
Dijkstra算法用于解决单源点最短路径问题,即给一个顶点作为源点,依次求它到图中其他n-1个顶点的最短距离。
例题讲解
Dijkstra算法将图中所有顶点分成两部分,第一部分是已知到源点最短距离的顶点Known(K),第二部分是不知道到源点最短距离的顶点Unknown(U)。初始化K中只有源点一个顶点,U中有n-1个顶点。如下图,我们求源点1到终点7的最短路径。
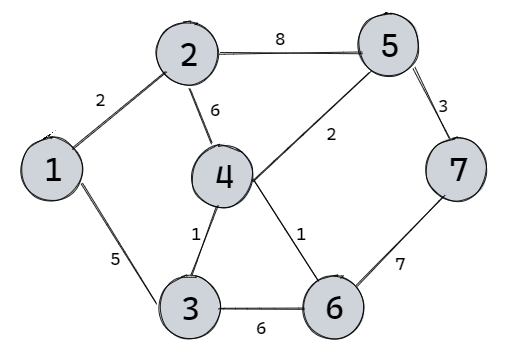
根据上图,可以得到如下表:
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 2 | 无穷 |
3 | 无穷 | ||
4 | 无穷 | ||
5 | 无穷 | ||
6 | 无穷 | ||
7 | 无穷 |
1-1. 找到顶点1的邻接点2和3,然后更新它们到源点1的距离得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 2 | 2 |
3 | 5 | ||
4 | 无穷 | ||
5 | 无穷 | ||
6 | 无穷 | ||
7 | 无穷 |
1-2. 更新K,U中的顶点。发现U中2到源点的距离最小,把2加入K中得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 3 | 5 |
2 | 2 | 4 | 无穷 |
5 | 无穷 | ||
6 | 无穷 | ||
7 | 无穷 |
2-1. 找到2的邻接点4和5,更新它们到源点的距离得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 3 | 5 |
2 | 2 | 4 | 6+2=8 |
5 | 8+2=10 | ||
6 | 无穷 | ||
7 | 无穷 |
2-2. 更新K,U中的顶点。发现U中3到源点距离最小,把3加入K中得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 4 | 8 |
2 | 2 | 5 | 10 |
3 | 5 | 6 | 无穷 |
7 | 无穷 |
3-1. 找到3的邻接点4和6,更新它们到源点的距离得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 4 | 5+1=6 |
2 | 2 | 5 | 10 |
3 | 5 | 6 | 6+5=11 |
7 | 无穷 |
3-2. 更新K,U中的顶点。发现U中4到源点的距离最短,把4加入K中得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 5 | 10 |
2 | 2 | 6 | 11 |
3 | 5 | 7 | 无穷 |
4 | 6 |
4-1. 找到4的邻接点5和6,更新它们到源点的距离得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 5 | 2+6=8 |
2 | 2 | 6 | 1+6=7 |
3 | 5 | 7 | 无穷 |
4 | 6 |
4-2. 更新K,U中的顶点。发现6到源点的距离最短,把6加入K中加入得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 5 | 8 |
2 | 2 | 7 | 无穷 |
3 | 5 | ||
4 | 6 | ||
6 | 7 |
5-1. 找到6的邻接点7,更新7到源点的距离得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 5 | 8 |
2 | 2 | 7 | 7+6=13 |
3 | 5 | ||
4 | 6 | ||
6 | 7 |
5-2. 更新K,U中的顶点。K中5到源点的距离最小把5加入K中得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 7 | 13 |
2 | 2 | ||
3 | 5 | ||
4 | 6 | ||
6 | 7 | ||
5 | 8 |
6-1. 找到5的邻接点7,更新7到源点的距离得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | 7 | 3+8=11 |
2 | 2 | ||
3 | 5 | ||
4 | 6 | ||
6 | 7 | ||
5 | 8 |
6-2. 更新K,U中的顶点,将顶点7加入K中完成计算得到下表
K | K中顶点到源点的距离 | U | U中顶点到源点的距离 |
1 | 0 | ||
2 | 2 | ||
3 | 5 | ||
4 | 6 | ||
6 | 7 | ||
5 | 8 | ||
7 | 11 |
由此我们就得到源点1到各个顶点的最短路径。
相关文章:

【期末复习】例题讲解Dijkstra算法
使用场景Dijkstra算法用于解决单源点最短路径问题,即给一个顶点作为源点,依次求它到图中其他n-1个顶点的最短距离。例题讲解Dijkstra算法将图中所有顶点分成两部分,第一部分是已知到源点最短距离的顶点Known(K),第二部分是不知道到…...

Pytorch 基础之张量索引
本次将介绍一下 Tensor 张量常用的索引与切片的方法: 1. index 索引 index 索引值表示相应维度值的对应索引 a torch.rand(4, 3, 28, 28) print(a[0].shape) # 返回维度一的第 0 索引 tensor print(a[0, 0].shape) # 返回维度一 0 索引位置…...
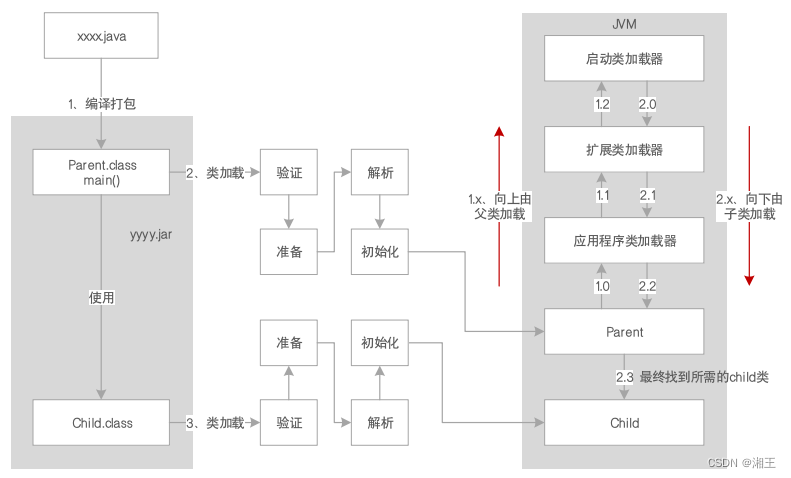
JVM系统优化实践(1):JVM概览
您好,我是湘王,这是我的CSDN博客,欢迎您来,欢迎您再来~这是多年之前做过的学习笔记,今天再翻出来,觉得仍然是记忆犹新。「独乐乐不如众乐乐」,就拿出来分享给「众乐乐」吧。目前大多…...

优秀!19年后,它再次成为TIOBE年度编程语言
新年伊始,TIOBE发布了2022年度编程语言,C时隔19年再度登顶,成为2022年最受欢迎的编程语言。TIOBE在2003年首次统计编程语言的流行指数时,C便成为年度编程语言。2022年,C获得了最高的人气4.62%,紧随其后的是…...
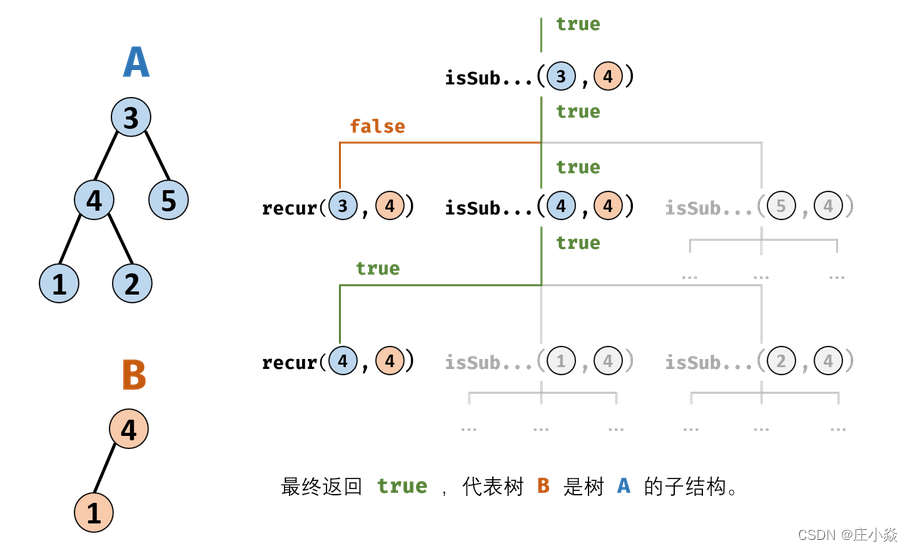
剑指 Offer 26. 树的子结构
摘要 剑指 Offer 26. 树的子结构 输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构),B是A的子结构, 即 A中有出现和B相同的结构和节点值。 一、子树解析 思路解析:若树B是树A的子结构,则…...

他是00年的,我们卷不过他...
现在的小年轻真的卷得过分了。前段时间我们公司来了个00年的,工作没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。 最近和他聊了一次天,原来这位小老弟家里条…...

C#开发的OpenRA的OpenGL创建纹理流程
C#开发的OpenRA的OpenGL创建纹理流程 由于OpenRA采用的是OpenGL来显示游戏画面, 那么它就必然采用纹理来显示了。 并且由于它是2D的游戏,所以3D的模型是没有的,只要使用纹理贴图,就可以完全实现了游戏的功能。 OpenGL的纹理要起作用,需要经过一系列的动作。 先要使用glGen…...
3D目标检测(一)—— 基于Point-Based方法的PointNet系列
3D目标检测(一)—— PointNet,PointNet,PointNeXt, PointMLP 目录 3D目标检测(一)—— PointNet,PointNet,PointNeXt, PointMLP 前言 零、网络使用算法 …...

《设计模式》策略模式
策略模式 前言 先了解一下设计模式的几种类似: 行为型设计模式(Behavioral Design Pattern)是指一组设计模式,它们关注的是对象之间的通信和协作。行为型设计模式描述了对象之间的职责分配和算法的封装,以及如何在运…...

【离散数学】1. 数理逻辑
1.数理逻辑 2. 集合论 3. 代数系统 4. 图论 离散数学:研究离散量结构及相互关系的学科 数理逻辑集合论代数系统图论 逻辑:研究推理的科学 数学方法:引进一套符号系统的方法 数理逻辑是用数学方法研究形式逻辑的科学,即使用符号化…...
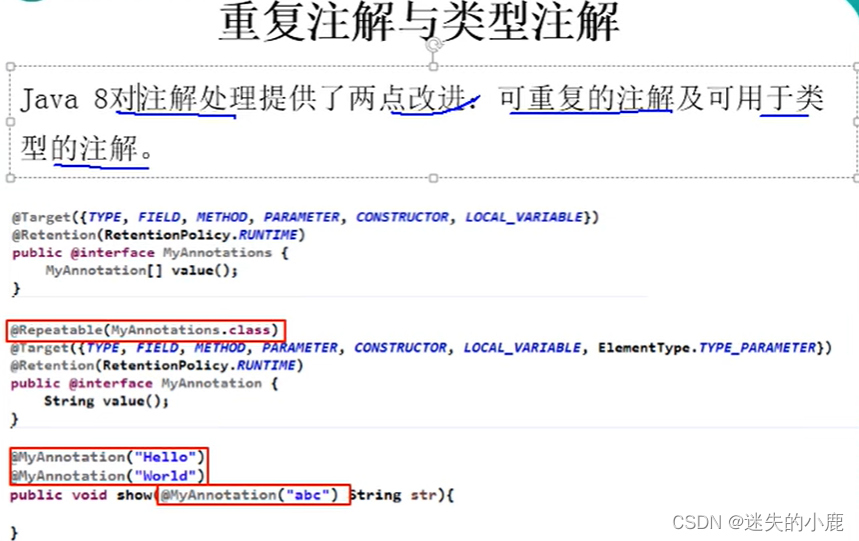
Java8新特性学习
Java8新特性学习为啥使用Lambda表达式Lambda表达式的基础语法无参无返回有参无返回一个参数多参单个语句体类型推断四大内置核心函数式接口其他接口方法引用与构造器引用Stream简介什么是StreamStream操作步骤创建Stream中间操作终止操作(终端操作)归约与收集并行流…...

SPARK outputDeterministicLevel的作用--任务全部重试或者部分重试
背景 目前spark的repartition()方法是随机分配数据到下游,这会导致一个问题,有时候如果我们用repartition方法的时候,如果任务发生了重试,就有可能导致任务的数据不准确,那这个时候改怎么解决这个问题呢? …...
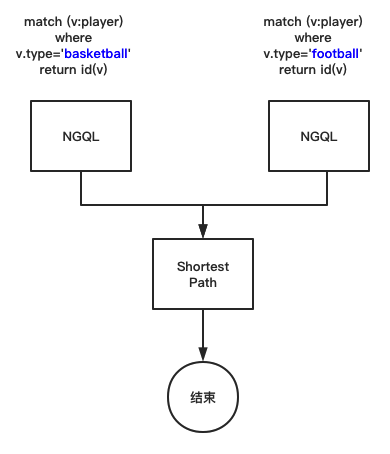
图数据库中的 OLTP 与 OLAP 融合实践
在一些图计算的场景下,我们会遇到同时需要处理 OLTP 和 OLAP 的问题。而本文就给了一个 OLTP 与 OLAP 融合实践的指导思路,希望给你带来一点启发。 Dag Controller 介绍 Dag Controller 是 NebulaGraph 企业版的图系统,经过反复测试无误后已…...

Shader Graph简介
使用着色器(shader)和材质(material),我们能够创造出非常多有趣的效果。除了Unity自带的shader外,还可以自己编写shader或使用其他人所编写的shader。编写shader通常需要我们了解shader编程语言的语法和相关…...

kubectl
目录 一、陈述式资源管理方法 二、基本信息查看 2.1 基本信息查看格式 2.2 查看master节点组件状态 2.3 查看命名空间 2.4 创建/查看命名空间 2.5 删除(重启)命名空间/pod 2.6 查看资源的详细信息 2.7 创建副本控制器来启动Pod 2.8 查看指定命…...

实验室设计SICOLAB第三方检测中心实验室设计
第三方检测中心实验室怎么设计?详细设计内容有哪些?功能区域有哪些?仪器有哪些?要多少面积?第三方检测中心实验室是一种独立的实验室,为客户提供各种测试和分析服务。以下是一个第三方检测中心实验室的详细…...

GPS经纬度转距离
function [pN, pE] distance_gps(lon1, lon2, lat1, lat2)d2r pi/180; % deg转radR 6371000.0; % 地球半径pN (lat2 - lat1) * d2r * R;pE (lon2 - lon1) * d2r * R * cos(lat2 * d2r); end...

7-周赛333总结
7-周赛333总结 还是只过了前两题,第三题又写了好久好久,然后也不知道错在了哪里,只过了部分题解,也许是思考不全面吧。下次也许先做第四题更好…第四题今天花了点时间 做出来了个大概 开心 :happy: 合并两个二维数组 - 求和法【…...

电子招标采购系统源码—互联网+招标采购
智慧寻源 多策略、多场景寻源,多种看板让寻源过程全程可监控,根据不同采购场景,采取不同寻源策略, 实现采购寻源线上化管控;同时支持公域和私域寻源。 询价比价 全程线上询比价,信息公开透明,可…...

SQL注入和XSS攻击
1、SQL注入 所谓SQL注入,就是通过把SQL命令插入到Web表单递交或输入域名或页面请求的查询字符串,最终达到欺骗服务器执行恶意的SQL命令。 我们永远不要信任用户的输入,我们必须认定用户输入的数据都是不安全的,我们都需要对用户输…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
