【管理运筹学】第 6 章 | 运输问题(4,表上作业法 |闭回路调整法以及特殊情况 | 产销不平衡的运输问题)
文章目录
- 引言
- 二、表上作业法
- 2.3 改进的方法 —— 闭回路调整法
- 2.4 表上作业法中的特殊情况
- (一)无穷多最优解
- (二)退化
- 三、产销不平衡的运输问题
- 3.1 产量大于销量
- 3.2 销量大于产量
- 写在最后
引言
接下来我们学习表上作业法的最后一步:改进,以及表上作业法中一些特殊的情况,还有关于产销不平衡问题的讨论。
二、表上作业法
表上作业法的求解工作在运输表上进行,运输问题解的每一个分量,都唯一对应其在运输表中的一个格子。它是一种迭代法,迭代步骤为:
先按某种规则找出一个初始解(初始调运方案),得出运输问题的一个基本可行解后,就可将基变量的值 x i j x_{ij} xij 填入运输表相应的格子内,并将这种格子称为填有数字格(可以含 0 ),非基变量对应格不填,称为空格。
接着对现有的解作最优性判别,若不是最优解,就在运输表上对其进行改进,得出一个新解;再判别,再改进;直至得到运输问题的最优解为止。
2.3 改进的方法 —— 闭回路调整法
闭回路调整法是改进当前基本可行解的方法,当表中空格处出现负检验数时,表明未得到最优解。
若有两个和两个以上的检验数,一般选其中最小的,以它对应的空格为调入格,即以它对应的非基变量为换入变量。在以此非基变量为顶点的闭回路中,选取偶数次顶点中最小的值对应的基变量为换出变量,此基变量的值作为调整量。
可以类比单纯形法中换出变量的确定。
闭回路中,奇数次顶点的值加上调整量,偶数次顶点的值减去调整量,得到新运输方案。
再次利用闭回路法或位势法,求各空格的检验数,若仍有负的检验数,重复上述步骤,直至所有检验数为非负。
2.4 表上作业法中的特殊情况
(一)无穷多最优解
产销平衡问题必存在最优解,那么有唯一解还是有无穷多最优解依据线性规划单纯形法最优解判别标准,即某个非基变量(空格)的检验数为 0 时,该问题有无穷多最优解。
(二)退化
在单纯形法确定换出变量时,有时存在两个或以上相同的最小比值 θ \theta θ ,这样在下一次迭代中就有一个或多个基变量的取值为 0 ,出现退化解。
在运输问题中,主要有以下两种情况:
(1)当确定初始解的各供求关系时,在 ( i , j ) (i,j) (i,j) 格填入数字后,出现 A i A_i Ai 处的余量等于 B j B_j Bj 处的需量,这时在产销平衡表上填一个数,而在单位运价表上相应地要划去一行和一列。为了使得最后有 ( m + n − 1 ) (m+n-1) (m+n−1) 个数字格,需要添加一个 “0” ,它的位置可能在对应同时划去的那一行或那一列的任一空格处。
(2)在用闭回路法调整时,在闭回路偶数次顶点上出现两个和两个以上相等的最小值。这时只能选择一个作为调入格,而经过调整后,得到退化解。这时有一个数字格则必须填入一个 0 ,表明它是基变量。当出现退化解后,可能在某闭回路偶数次顶点上有取值为 0 的数字格,应取调整量为 0 。
三、产销不平衡的运输问题
之前所介绍了表上作业法是以产销平衡为前提的,但是实际问题中,产销往往是不平衡的,因此需要把产销不平衡问题转化为产销平衡问题。
3.1 产量大于销量
总产量大于总销量时,约束条件不再全是等式。关于销量仍需为等式,但是关于产量的约束为 " ≤ " "\leq" "≤" ,其数学模型如下:

在前 m m m 个不等式中加入松弛变量,则有 ∑ j = 1 n x i j + x i , n + 1 = a i ( i = 1 , 2 , … , m ) \sum_{j=1}^nx_{ij}+x_{i,n+1}=a_i(i=1,2,\dots,m) j=1∑nxij+xi,n+1=ai(i=1,2,…,m) 接着,虚拟一个销售地 B n + 1 B_{n+1} Bn+1 ,其需求量为 b n + 1 = ∑ i = 1 m a i − ∑ j = 1 n b j b_{n+1}=\sum_{i=1}^ma_i-\sum_{j=1}^nb_j bn+1=i=1∑mai−j=1∑nbj 于是,松弛变量 x i , n + 1 x_{i,n+1} xi,n+1 可以看作是产地 A i A_i Ai 运往销售地 B n + 1 B_{n+1} Bn+1 的物品数量,相应的运费取 0 。这样一来,就转化为了一个产销平衡的运输问题
3.2 销量大于产量
此时关于产量约束取不等式,其数学模型如下:

可假设一个虚拟产地 A m + 1 A_{m+1} Am+1 ,其产量为总销量和总产量之差,到各个销地的运费取 0 ,即可化为一个产销平衡的运输问题。
若求解后得到 x m + 1 , j = 0 x_{m+1,j}=0 xm+1,j=0 ,表明销售地 B j B_j Bj 需求满足;若 x m + 1 , j > 0 x_{m+1,j}>0 xm+1,j>0 ,表明销售地 B j B_j Bj 需求未得到满足,需要自行解决,解决的数量为 x m + 1 , j . x_{m+1,j}. xm+1,j.
有时候可能出现一个销售地的需求有好几部分,比如最低需求是 a a a ,最高需求是 b b b 等等。实际上可以将这个销售地看作两个地区,第一个地区的需求为 a a a ,第二个地区的需求为 b − a . b-a. b−a.
但此时,虚拟产地到第一个地区的运费应设为 M M M(无限大),因为其约束方程为 " ≥ " "\geq" "≥" 。
写在最后
完完整整的表上作业法做下来可不轻松,比较费时间,重要的应该还是其思想,以及和之前的单纯形法互通的地方。
相关文章:

【管理运筹学】第 6 章 | 运输问题(4,表上作业法 |闭回路调整法以及特殊情况 | 产销不平衡的运输问题)
文章目录 引言二、表上作业法2.3 改进的方法 —— 闭回路调整法2.4 表上作业法中的特殊情况(一)无穷多最优解(二)退化 三、产销不平衡的运输问题3.1 产量大于销量3.2 销量大于产量 写在最后 引言 接下来我们学习表上作业法的最后…...

Greenplum实用技巧
一、通过gp_segment_id查看数据倾斜 gp_segment_id是表中的隐藏列,用来标记该行属于哪个segment节点。因此可以基于该隐藏列进行分组查询,获取每个segment的记录数,从而判断表数据的分布是否均匀或有倾斜。 qb#select gp_segment_id, count…...
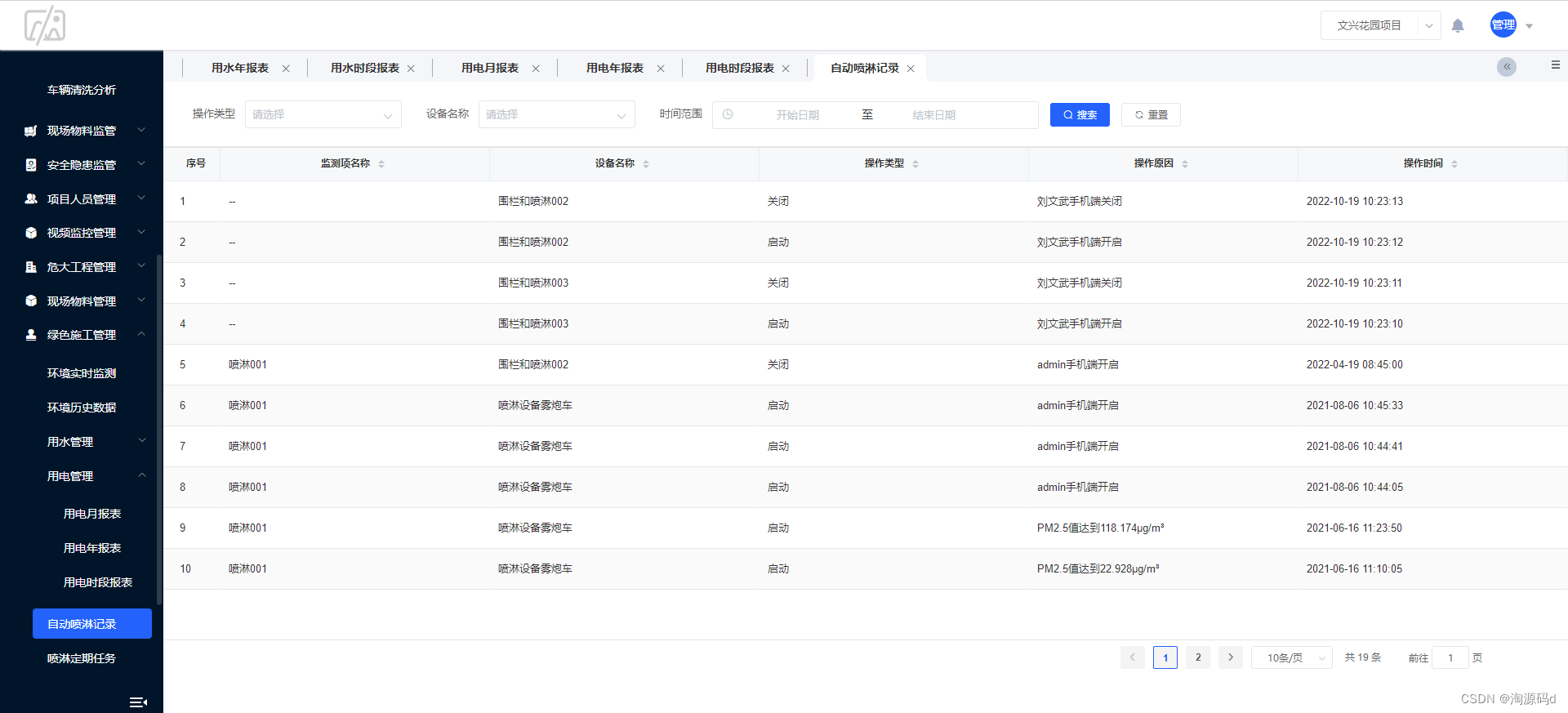
以物联网为核心的智慧工地云平台:聚集智能技术,实现建筑工地智慧管理
智慧工地云平台源码,智慧工地项目监管平台源码,智慧工地可视化数据大屏源码 智慧工地云平台是将云计算、大数据、物联网、移动技术和智能设备等信息化技术手段,聚集在建筑工地施工管理现场,围绕人员、机械、物料、环境等关键要素&…...
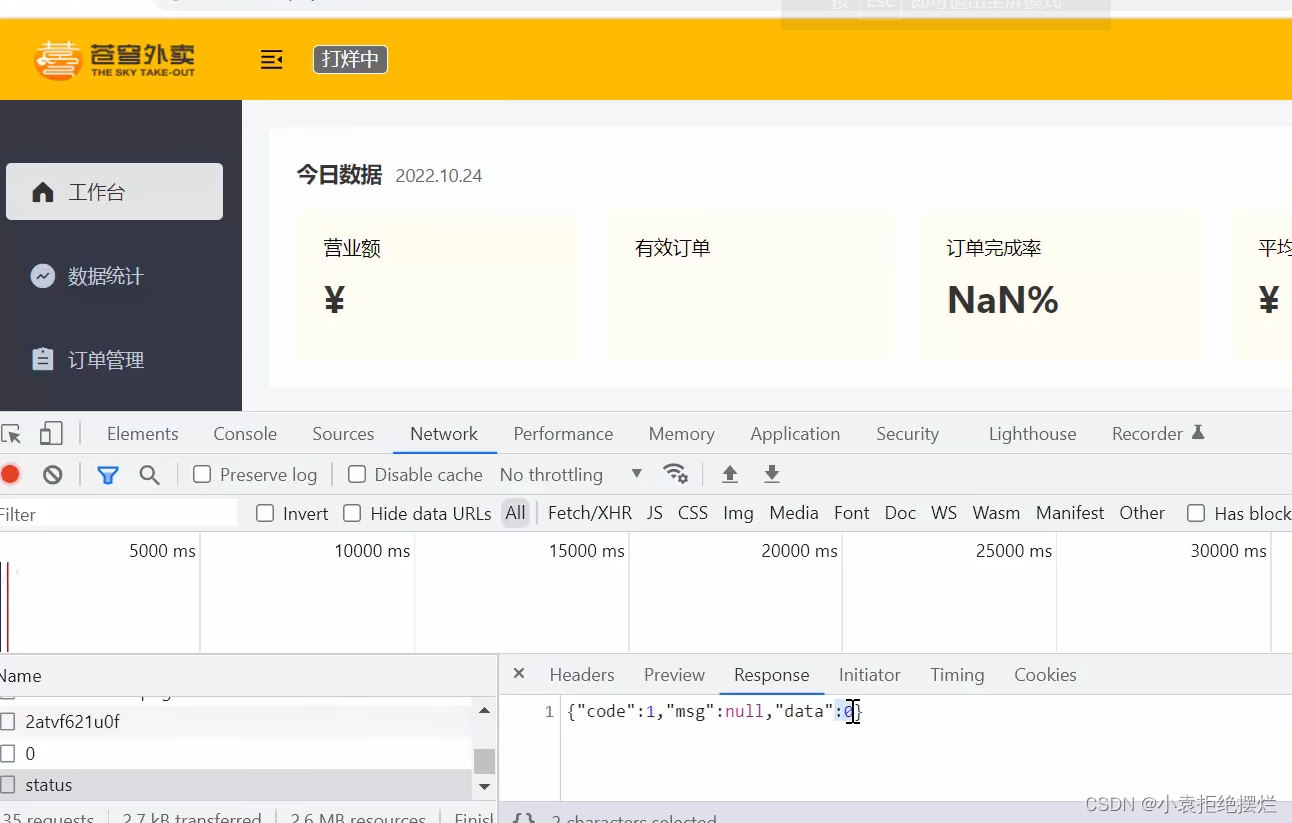
Java项目-苍穹外卖-Day05-Redis技术应用
1.店铺营业状态设置 需求分析和设计 左上角要求是有回显的 所以至少两个接口 1.查询营业状态接口(分为了管理端和用户端) 2.修改营业状态接口 因为管理端和用户端路径不同,所以现在是至少三个接口的 可以发现如果存到表里除了id只有一个…...

linux安装jmeter
linux安装jmeter 部署java1.8 下载jmeter安装包:官网、网盘5.6.2版本 # 解压 rootiZbp1at7nu2rpq4xn4zaf1Z:/opt/jmeter# sudo tar -xzf apache-jmeter-5.6.2.tgz # 加入环境变量 rootiZbp1at7nu2rpq4xn4zaf1Z:/opt/jmeter/apache-jmeter-5.6.2# export JMETER/op…...

【笔记】泛型以及如何绕过泛型定义
泛型定义以及其带来的好处 泛型使类型(类和接口)能够在定义类、接口和方法时成为参数。与方法声明中使用的更熟悉的形式参数非常相似,类型参数为您提供了一种通过不同输入重复使用相同代码的方法。区别在于形式参数的输入是值,而…...
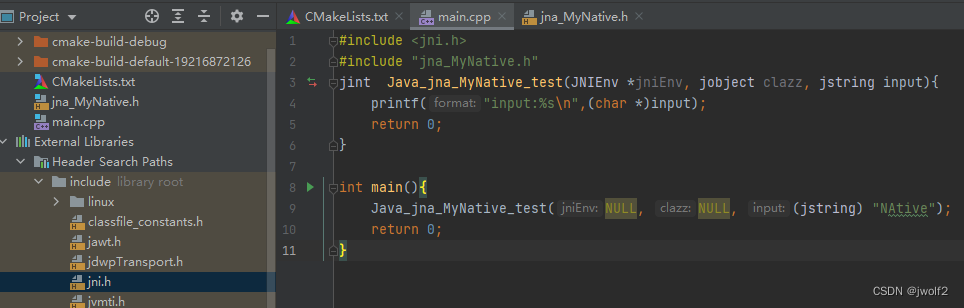
JAVA JNA 调用C接口的三种方式
文章目录 1. 准备一个共享库文件2. JNA姿势1—继承Library接口3. JNA姿势2—直接NativeLibrary.getInstance3. JNA姿势3—Native方法 1. 准备一个共享库文件 test.c #include <stdio.h> int test(char *input){printf("input:%s\n",input);return 0; }libtes…...

StarRocks入门到熟悉
1、部署 1.1、注意事项 需要根据业务需求设计严谨的集群架构,一般来说,需要注意以下几项: 1.1.1、FE数量及高可用 FE的Follower要求为奇数个,且并不建议部署太多,通常我们推荐部署1个或3个Follower。在三个Followe…...
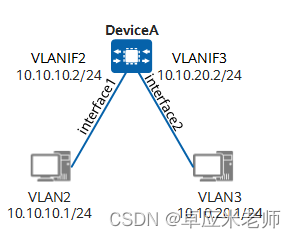
华为AR路由器 典型配置案例——以太网交换
目录 Eth-Trunk 例:配置三层链路聚合 组网需求 操作步骤 检查配置结果 配置脚本 VLAN 举例:配置基于接口划分VLAN,实现同一VLAN内的互通(同设备) 组网需求 操作步骤 检查配置结果 配置脚本 举例ÿ…...
DP读书:鲲鹏处理器 架构与编程(十三)操作系统内核与云基础软件
操作系统内核与云基础软件 鲲鹏软件构成硬件特定软件 鲲鹏软件构成硬件特定软件1. Boot Loader2. SBSA 与 SBBR3. UEFI4. ACPI 操作系统内核Linux系统调用Linux进程调度Linux内存管理Linux虚拟文件系统Linux网络子系统Linux进程间通信Linux可加载内核模块Linux设备驱动程序Linu…...
Vue2项目练手——通用后台管理项目第一节
Vue2项目练手——通用后台管理项目 知识补充yarn和npm区别npm的缺点:yarn的优点 npm查看镜像和设置镜像 项目介绍项目的技术栈 项目搭建文件目录 创建路由,引入element-uirouter/index.jsmain.jspages/Users.vuepages/Main.vuepages/Home.vuepages/Login…...

「Vue|网页开发|前端开发」02 从单页面到多页面网站:使用路由实现网站多个页面的展示和跳转
本文主要介绍如何使用路由控制来实现将一个单页面网站扩展成多页面网站,包括页面扩展的逻辑,vue的官方路由vue-router的基本用法以及扩展用法 文章目录 本系列前文传送门一、场景说明二、基本的页面扩展页面扩展是在扩什么创建新页面的代码,…...
缓存配置)
【Nginx20】Nginx学习:FastCGI模块(二)缓存配置
Nginx学习:FastCGI模块(二)缓存配置 通过上篇文章的学习,普通的 PHP 与 Nginx 的连接就已经没啥大问题了。一般的网站直接那套配置就够了,这也是 Nginx 非常友好的一面。很多在默认的配置文件中注释掉的内容࿰…...
苹果支付外包开发流程
苹果支付的实现流程主要涉及集成苹果的支付系统——Apple Pay,以及在你的应用中处理支付交易。以下是一个简要的实现流程概述,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1.开发者账号…...
银河麒麟V10(Tercel)服务器版安装 Docker
一、服务器环境 ## 查看系统版本,确认版本 cat /etc/kylin-release Kylin Linux Advanced Server release V10 (Tercel)## 操作系统 uname -p aarch64## 内核版本(≥ 3.10) uname -r 4.19.90-21.2.ky10.aarch64## iptables 版本(…...
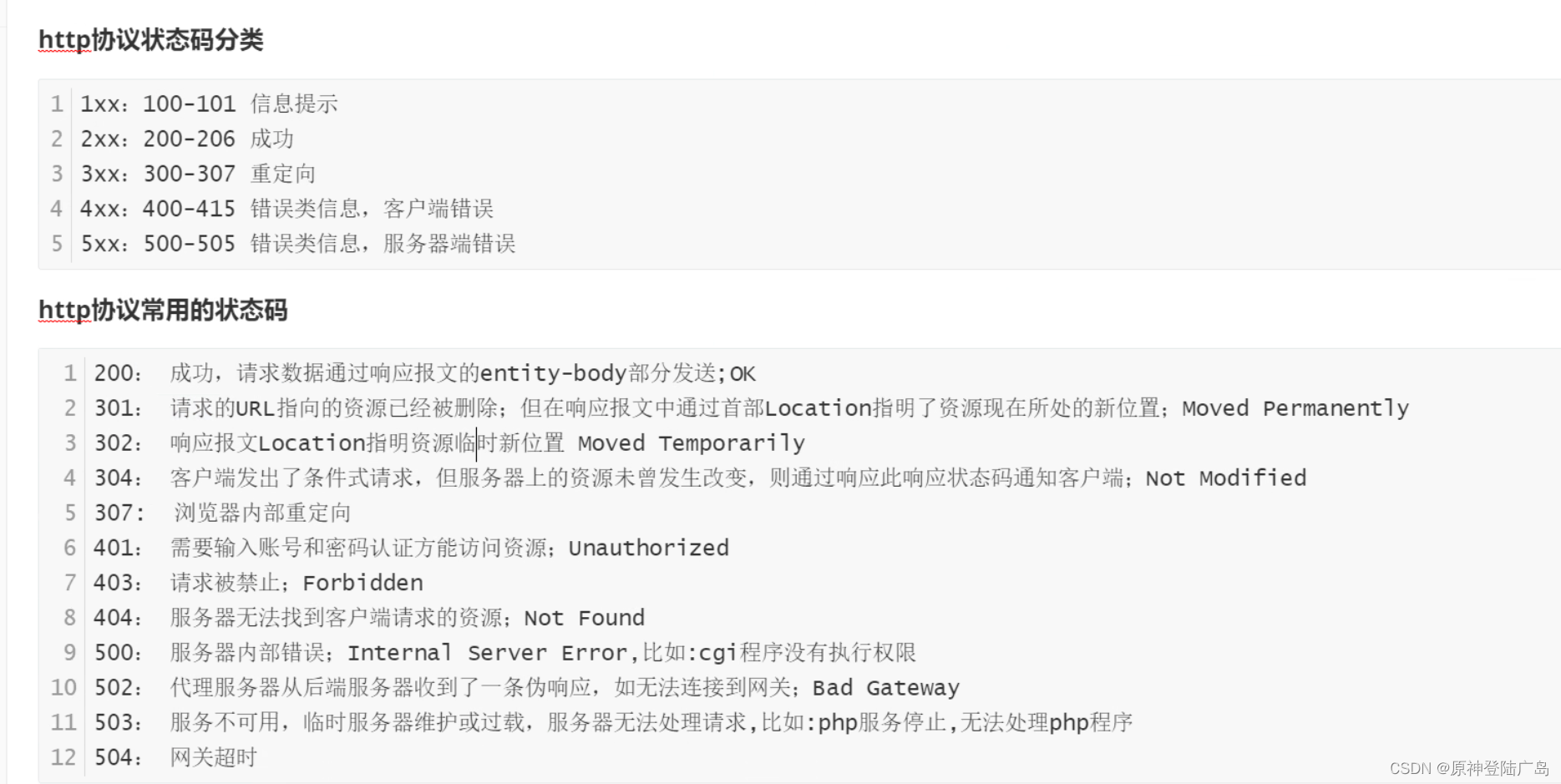
web、HTTP协议
目录 一、Web基础 1.1 HTML概述 1.1.1 HTML的文件结构 1.2 HTML中的部分基本标签 1.3 URI 和 URL 二.HTTP协议 2.1.HTTP概念 2.2.HTTP协议版本 2.3.HTTP请求方法 2.4.HTTP请求访问的完整过程 2.5.HTTP状态码 2.6.HTTP请求报文和响应报文 2.7.HTTP连接优化 三.HTT…...

达梦SQL书写注意事项
模糊查询 模糊查询like后面的字段要求用单引号引用,不能使用双引号 select * from user where name like %小组 分组查询 select查询的列字段必须在分组中的字段存在 正确: select name,age from user group by name,age 错误: select * f…...
博途1200脉冲输出控制速度轴(轴工艺对象基本配置)
这里的1200脉冲轴,主要用来完成线缆包材绕包时的重叠率控制。关于重叠率的具体概念,这里不再阐述,大家可以看下面的文章链接, 重叠率控制 重叠率控制(算法详细介绍含SCL和梯形图源代码)_RXXW_Dor的博客-CSDN博客产品包装和线缆保护材料的包覆都需要进行材料包装重叠率的控…...

微信小程序 通过setData 给两个变量设置同一个数组时,为什么修改一个变量,另一个会也被修改?
在微信小程序中,使用 setData 方法更新数据时,如果给两个变量设置同一个数组,修改其中一个变量的值会导致另一个变量也被修改的原因是,数组是引用类型的数据,在内存中的存储方式是按引用地址存储。 当你将一个数组赋值…...

保障Web安全:构建可靠的网络防御体系
在当今数字化时代,Web安全已成为互联网世界中至关重要的议题。随着网络攻击手段的不断演进和网络犯罪的增加,保护用户数据和确保系统安全性已成为任何Web应用程序的首要任务。本文将深入探讨Web安全的重要性以及构建可靠的网络防御体系的关键要素。我们将…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
