力扣:75. 颜色分类(Python3)
题目:
给定一个包含红色、白色和蓝色、共
n个元素的数组nums,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。我们使用整数
0、1和2分别表示红色、白色和蓝色。必须在不使用库内置的 sort 函数的情况下解决这个问题。
来源:力扣(LeetCode)
链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
示例:
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:输入:nums = [2,0,1]
输出:[0,1,2]
解法:
使用列表内置函数sort。
代码:
class Solution:def sortColors(self, nums: List[int]) -> None:"""Do not return anything, modify nums in-place instead."""nums.sort()
相关文章:
)
力扣:75. 颜色分类(Python3)
题目: 给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。 我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。 必须在不使用库内置的 sort …...
JVM 内存大对象监控和优化实践
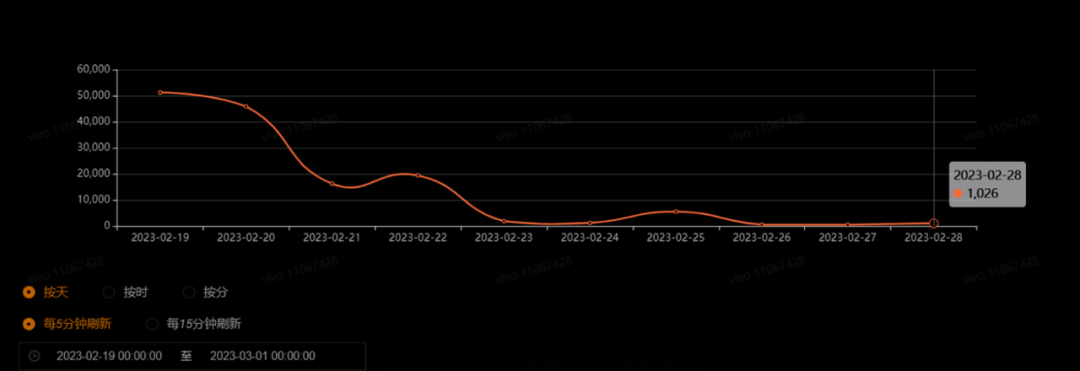
作者:vivo 互联网服务器团队 - Liu Zhen、Ye Wenhao 服务器内存问题是影响应用程序性能和稳定性的重要因素之一,需要及时排查和优化。本文介绍了某核心服务内存问题排查与解决过程。首先在JVM与大对象优化上进行了有效的实践,其次在故障转移与…...

vue indexedDB 取指定数据库指定表 全部key用request.onsuccess
1 例子 export async function funcGetKey(dbName, tableName) {return new Promise((resolve, reject) > {// 打开指定的数据库const request indexedDB.open(dbName);request.onerror (event) > {console.error(打开数据库失败: , event.target.error);reject(event…...

Java 数据结构使用学习
Set和List的区别 Set 接口实例存储的是无序的,不重复的数据。List 接口实例存储的是有序的,可以重复的元素。 Set 检索效率低下,删除和插入效率高,插入和删除不会引起元素位置改变 <实现类有HashSet,TreeSet>。 List 和数…...
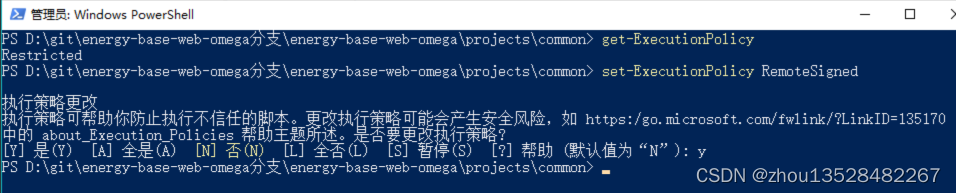
monorepo更新组件报错,提示“无法加载文件 C:\Program Files\nodejs\pnpm.ps1,因为在此系统上禁止运行脚本”
解决方法: 第一步:管理员身份运行 window.powershell, win x打开powerShell命令框,进入到对应项目路径。 第二步:执行:get-ExecutionPolicy,显示Restricted,表示状态是禁止的; 第…...

vue中html引入使用<%= BASE_URL %>变量
首先使用src相对路径引入 注意: js 文件放在public文件下 不要放在assets静态资源文件下 否则 可能会报错 GET http://192.168.0.113:8080/src/assets/js/websockets.js net::ERR_ABORTED 500 (Internal Server Error) 正确使用如下:eg // html中引…...

Android全面屏下,默认不会全屏显示,屏幕底部会留黑问题
前些天发现了一个蛮有意思的人工智能学习网站,8个字形容一下"通俗易懂,风趣幽默",感觉非常有意思,忍不住分享一下给大家。 👉点击跳转到教程 公司以前的老项目,便出现了这种情况,网上搜索了各种资料…...
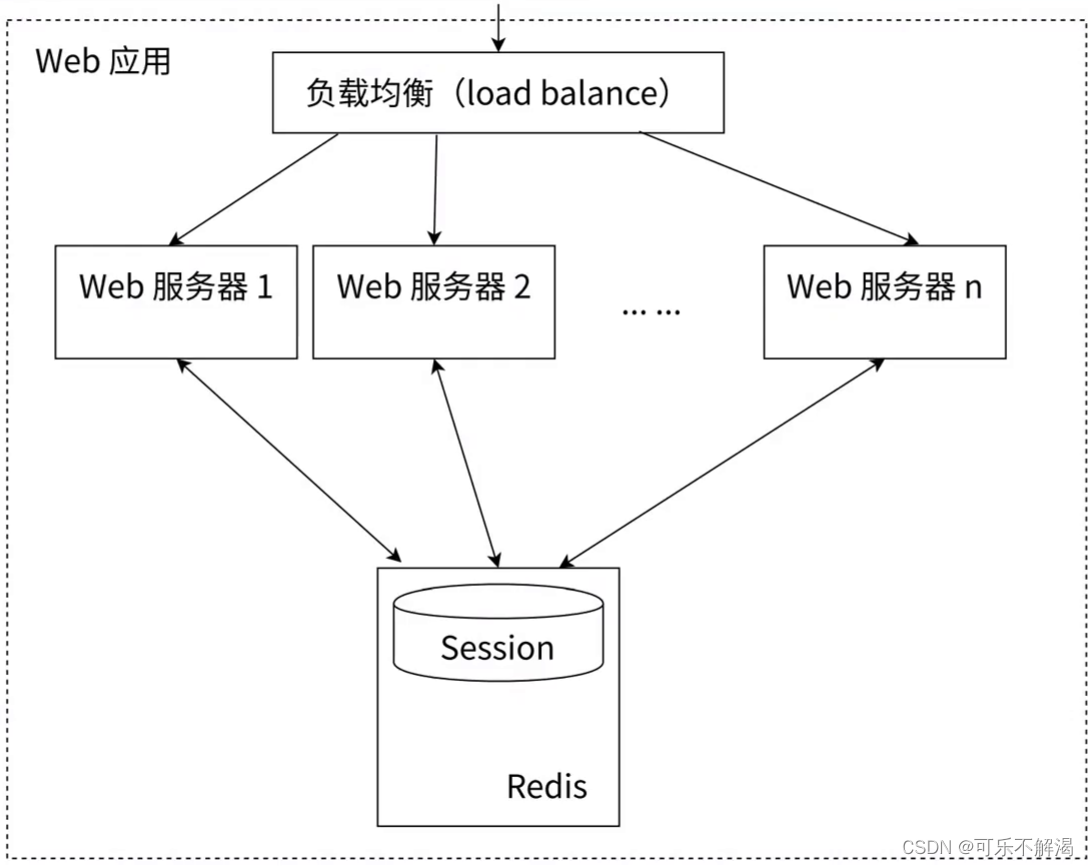
5.Redis-string
string 字符串 字符串类型是 Redis 最基础的数据类型,关于字符串需要特别注意: 1.⾸先Redis中所有 key 的类型都是字符串类型,⽽且其他⼏种数据结构也都是在字符串类似基础上构建的,例如 list 和 set 的元素类型是字符串类型。 2…...
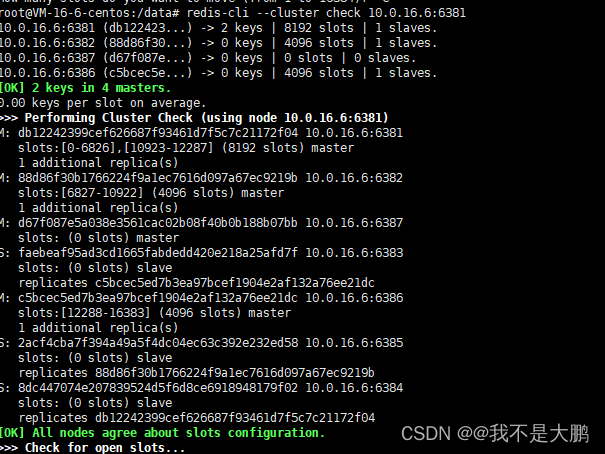
docker高级(redis集群三主三从)
1. 新建6个docker容器redis实例 docker run -d --name redis-node-1 --net host --privilegedtrue -v /redis/share/redis-node-1:/data redis:6.0.8 --cluster-enabled yes --appendonly yes --port 6381docker run -d --name redis-node-2 --net host --privilegedtrue -v /…...
linux 设置与命令基础(二)
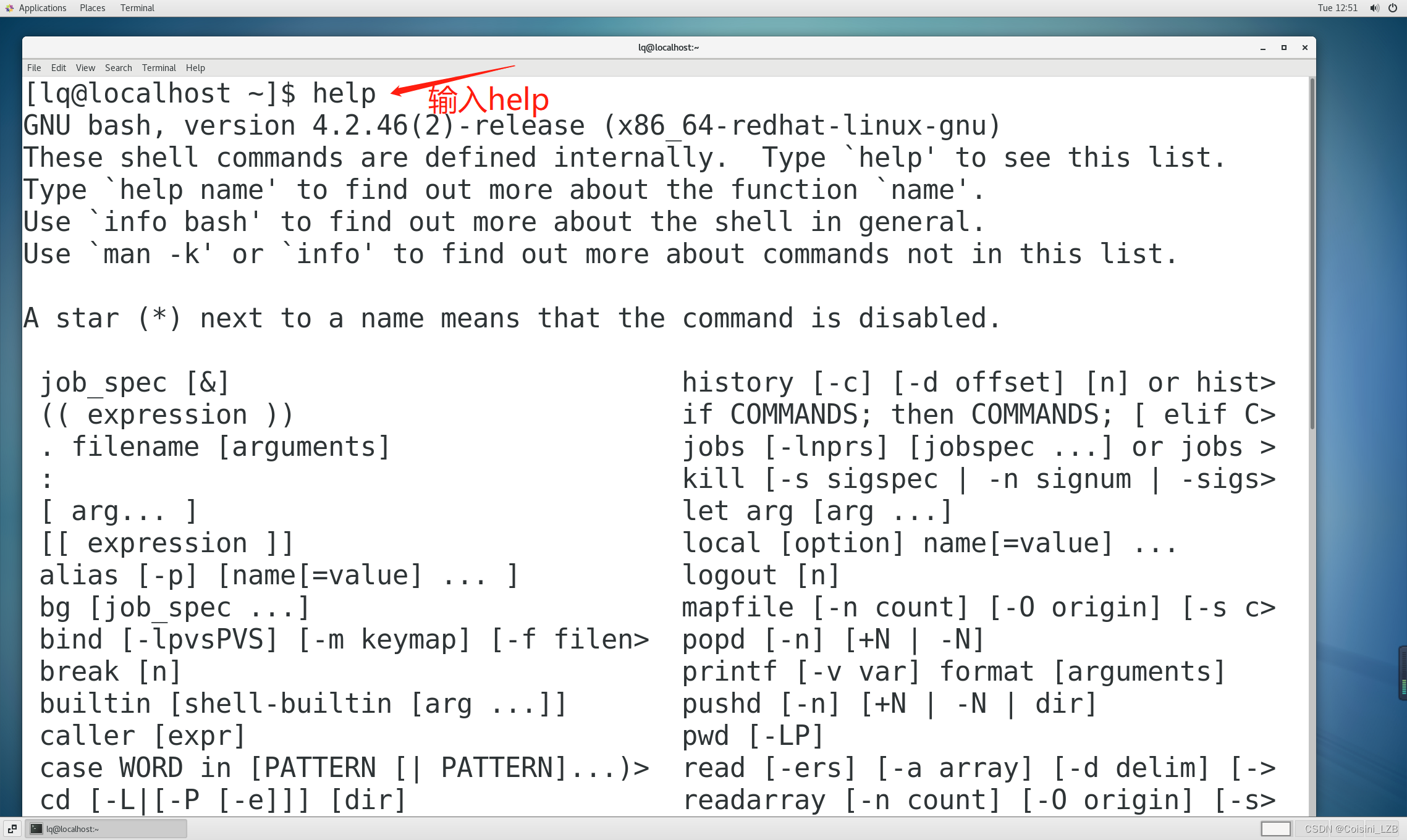
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、系统基本操作 二、命令类型 三、命令语法 四、命令补齐 五、命令帮助 六、系统基本操作命令 总结 前言 这是本人学习Linux的第二天,今天主…...

ubuntu20.04中ros2安装rosbridge及启动方式
ros2 启动rosbridge: 要启动ROS2中的rosbridge,需要先安装ROS2的rosbridge_suite软件包。使用以下命令安装: sudo apt-get update sudo apt-get install ros-<distro>-rosbridge-suite将<distro>替换为正在使用的ROS2发行版的名…...

TCP之超时重传、流量控制和拥塞控制
一、超时重传 TCP超时重传是TCP协议中的一种机制,用于在发生丢包或数据包未及时确认的情况下,重新发送未确认的数据段。 当发送方发送一个数据段后,会启动一个定时器(称为超时计时器),等待接收方的确认。…...

git clone 报SSL证书问题
git命令下运行 git config --global http.sslVerify false 然后再进行重新clone代码...

Spring Boot 排除配置类的引用的方法
Spring Boot 提供的自动配置非常强大,某些情况下,自动配置的功能可能不符合我们的需求,需要我们自定义配置,这个时候就需要排除/禁用 Spring Boot 某些类的自动化配置了。 比如:数据源、邮件,这些都是提供…...
代码随想录打卡—day46—【DP】— 8.29 背包END
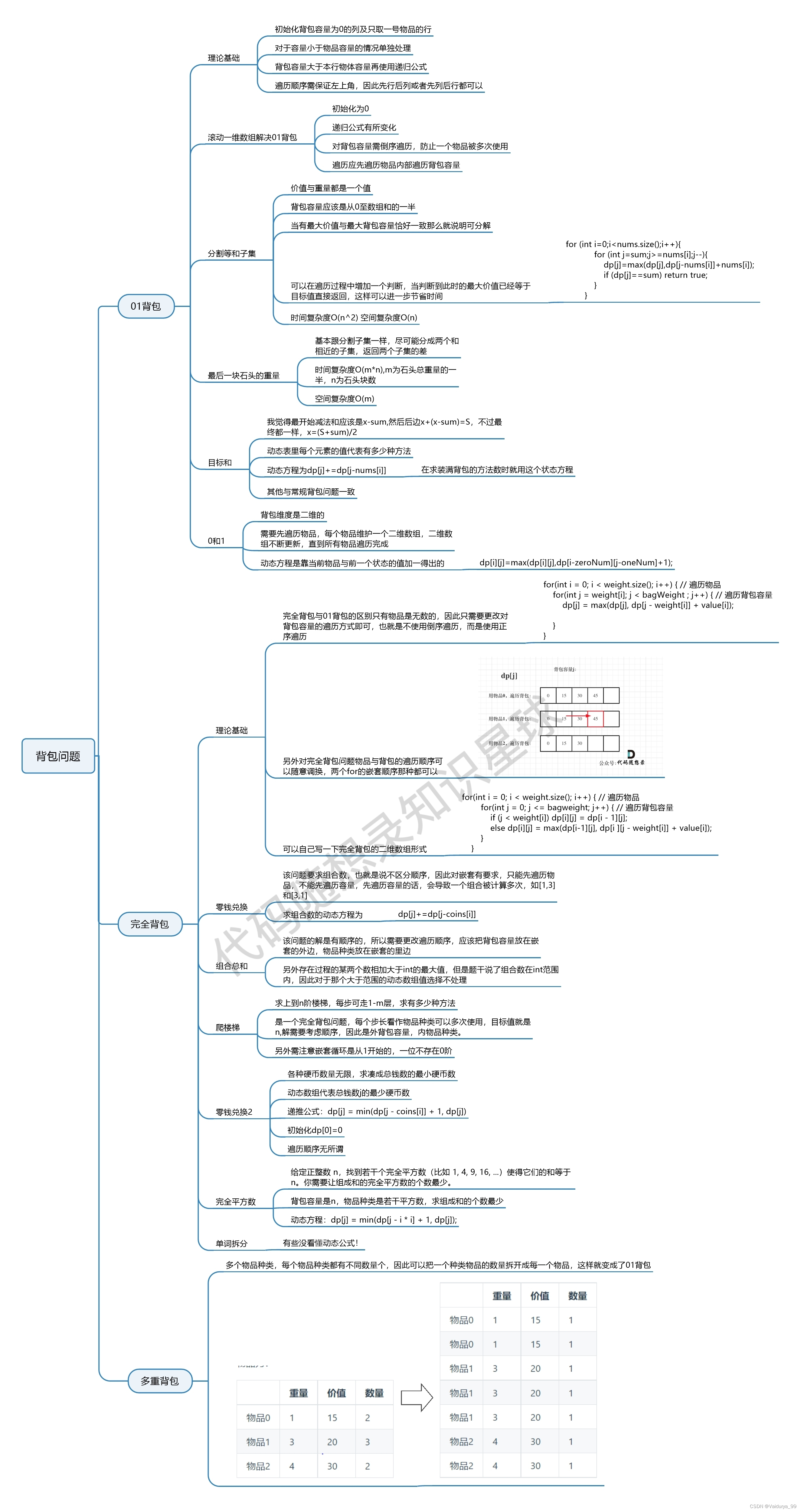
1 139. 单词拆分 139. 单词拆分 做了很久...估计2h 一开始我的思路卡死了 看题解之后的思路的详解见注释, 我的写法和carl 答案在一些微小的细节上略有不同,我的更好理解,但他的解法更简单。 我写的过程中,需要注意下标和字符…...

lua学习-3 循环和流程控制
这里写目录标题 判断for 循环数值遍历泛型遍历遍历数组遍历对象ipairs 和 pairs的异同 while 循环repeat循环goto基础用法注意事项 判断 for 循环 数值遍历 for exp1,exp2,exp3 do//todoend上述代码是指:从exp1 到exp2 以exp3为步长进行循环并执行todo代码&#…...
3、监测数据采集物联网应用开发步骤(3)
监测数据采集物联网应用开发步骤(2) 系统整体结构搭建 新建项目 输入项目名称:MonitorData 所谓兵马未动粮草先行,按下图创建好对应的模块备用: com.plugins 业务插件模块 com.zxy.adminlog 日志或文本文…...

MySQL用户管理及用户权限
目录 数据库用户管理 新建用户 查看用户 重命名用户rename 删除用户drop 修改用户密码 找回root密码 数据库用户授权 授予权限 查看用户权限 撤销用户权限 数据库用户管理 新建用户 CREATE USER 用户名来源地址 [IDENTIFIED BY [PASSWORD] 密码];用户名:…...

Yolov8-pose关键点检测:模型轻量化创新 | PConv结合c2f | CVPR2023 FasterNet
💡💡💡本文解决什么问题:新的partial convolution(PConv),通过同时减少冗余计算和内存访问可以更有效地提取空间特征。 PConv| GFLOPs从9.6降低至8.5,参数量从6482kb降低至6134kb, mAP50从0.921提升至0.925 Yolov8-Pose关键点检测专栏介绍:https://blog.csdn.n…...

聊聊mybatis-plus的SafetyEncryptProcessor
序 本文主要研究一下mybatis-plus的SafetyEncryptProcessor SafetyEncryptProcessor mybatis-plus-boot-starter/src/main/java/com/baomidou/mybatisplus/autoconfigure/SafetyEncryptProcessor.java public class SafetyEncryptProcessor implements EnvironmentPostProc…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
