区间型动态规划典型题目:lintcode 476 · 石子归并【中等,免费】lintcode 593 · 石头游戏 II【中等 vip】
题目lintcode476 链接,描述
https://www.lintcode.com/problem/476/description
有一个石子归并的游戏。最开始的时候,有n堆石子排成一列,目标是要将所有的石子合并成一堆。合并规则如下:每一次可以合并相邻位置的两堆石子
每次合并的代价为所合并的两堆石子的重量之和
求出最小的合并代价。样例
样例 1:输入: [3, 4, 3]
输出: 17
样例 2:输入: [4, 1, 1, 4]
输出: 18
解释: 1. 合并第二堆和第三堆 => [4, 2, 4], score = 22. 合并前两堆 => [6, 4],score = 83. 合并剩余的两堆 => [10], score = 18
题目lintcode593 链接,描述
https://www.lintcode.com/problem/593
有一个石头游戏。在游戏的开始的时候,玩家挑选了 n 堆石头并围成一个 圈,即第一堆石头与最后一堆石头相邻。目标是按照下面的规则将石头合并成一堆:在游戏中的每一步,玩家可以合并两堆相邻的石头为新的一堆石头。分数就是新的石头堆的石头个数。你需要找到最小的总分。样例
例1:输入:
[1,1,4,4]
输出:18
解释:
1.合并前两个=> [2,4,4],得分+2
2.合并前两个=> [6,4],得分+6
3.合并最后两个=> [10],得分+10
例2:输入:
[1,1,1,1]
输出:8
解释:
1.合并前两个=> [2,1,1],得分+2
2.合并后两个=> [2,2],得分+2
3.合并最后两个=> [4],得分+4
思路
lintcode: 476从最小长度的i~j开始做dp,因为长的i~j肯定能从比他小的段计算出来
算法:区间DP
这是一道区间DP问题,我们需要用区间表示状态来递推。设s是表示石头重量的数组,设f[i][j]是将s[i,…,j]的石头合并成一个所需的最少能量,那么这个最少能量按照最后一步合并的分界线可以分为以下几种情况:
1、最后一步是s[i]和s[i+1,…,j]合并,此时需要的最少能量是f[i+1][j]+sum(s[i]…s[j]),第一项是合并后者需要的能量,第二项是最后一次合并所需要的能量。s[i]自己只有一个石头,不需要合并
2、最后一步是s[i,i+1]和s[i+2,…,j]合并,此时需要的最少能量是f[i][i+1]+f[i+2][j]+sum(s[i]…s[j]),第一项是合并前两个石头需要的能量,第二项是合并后半区间石头需要的能量,最后一项是最后一次合并需要的能量;
从上面我们可以看出一个规律,f[i][j]应该是所有区间分法中前一半区间的石头合并需要的总能量加上后半区间的总能量再加上最后一次合并需要的能量
求得A的前缀和
区间长度从2开始枚举,
根据上诉思路可得递推式
dp[l][r] =min(dp[l][r], dp[l][j] + dp[j + 1][r] + sum_a[r + 1] - sum_a[l])
记得初始化dp[l][r]为一个较大值
结果存在dp[0][size-1]中
复杂度分析
时间复杂度O(n^3)
区间dp的复杂度
空间复杂度O(n^2)
dp数组的大小
1.算法
区间型动态规划,线变成环,一般的两种方法,求补集,或者枚举接口处,类似House Robber
II. 这里都不适用。 采用第三种方法:将数组变成2倍,取长度为n的最小值
2.代码实现注意
可以直接lintcode 476的答案,只不过数组长度n扩充为原来的2倍也就是2*n,求解过程中,动态规划最外层循环i%n==0时候,记录最小值,最小值就是答案
题目lintcode 476答案
public class Solution {/*** @param a: An integer array* @return: An integer*/public int stoneGame(int[] a) {//从最小长度的i~j开始做dp,因为长的i~j肯定能从比他小的段计算出来if(a ==null || a.length==0) return 0;int n= a.length;int[][] dp = new int[n+1][n+1];int[] sum = new int[n+1];for (int i = 1; i <=n ; i++) {sum[i] = sum[i-1]+a[i-1];}for (int len = 2; len <=n ; len++) {for (int i = 1; i+len-1 <=n ; i++) {int j= i+len-1;dp[i][j] = Integer.MAX_VALUE;for (int k = i; k <j ; k++) {dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);}}}return dp[1][n];}
}
题目 lintcode 593 答案
public class Solution {/*** @param a: An integer array* @return: An integer*/public int stoneGame2(int[] a) {/*1.算法区间型动态规划,线变成环,一般的两种方法,求补集,或者枚举接口处,类似House Robber II. 这里都不适用。采用第三种方法:将数组变成2倍,取长度为n的最小值2.代码实现注意k的下标迷之tle了3.时空复杂度分析时间复杂度 : O(n^2)空间复杂度 : O(n^2)*/if(a==null || a.length<2) return 0;int n = a.length;int[] arr1 = new int[n*2];for (int i = 0; i <2*n ; i++) {arr1[i]= a[i%n];}return stoneGame(arr1);}//下面的代码和lintcode 476题代码差不多,不同的是:本地数组长度变为原来的2倍//因此在新数组求解过动态规划程中,需要len==n/2的时候,得到最小值,就是答案public static int stoneGame(int[] a) {//从最小长度的i~j开始做dp,因为长的i~j肯定能从比他小的段计算出来if(a== null || a.length ==0)return 0;int n = a.length;int[][] dp = new int[n+1][n+1];int[] sum = new int[n+1];for (int i = 1; i <=n ; i++) {sum[i] =sum[i-1]+a[i-1];}int min = Integer.MAX_VALUE;for (int len = 2; len <=n ; len++) {for (int i = 1; i+len-1 <=n ; i++) {int j = i+len-1;dp[i][j] = Integer.MAX_VALUE;for (int k = i; k <j ; k++) {dp[i][j] = Math.min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);if(len == n/2){min=Math.min(min,dp[i][j]);//.out.println("index:-- "+len);}}}}return min;}
}
相关文章:

区间型动态规划典型题目:lintcode 476 · 石子归并【中等,免费】lintcode 593 · 石头游戏 II【中等 vip】
题目lintcode476 链接,描述 https://www.lintcode.com/problem/476/description 有一个石子归并的游戏。最开始的时候,有n堆石子排成一列,目标是要将所有的石子合并成一堆。合并规则如下:每一次可以合并相邻位置的两堆石子 每次…...
4. 池化层相关概念
4.1 池化层原理 ① 最大池化层有时也被称为下采样。 ② dilation为空洞卷积,如下图所示。 ③ Ceil_model为当超出区域时,只取最左上角的值。 ④ 池化使得数据由5 * 5 变为3 * 3,甚至1 * 1的,这样导致计算的参数会大大减小。例如1080P的电…...
ChatGPT Prompting开发实战(一)
一、关于ChatGPT Prompting概述 当我们使用ChatGPT或者调用OpenAI的API时,就是在使用prompt进行交互,用户在对话过程中输入的一切信息都是prompt(提示词),当然工业级的prompt与人们通常理解的prompt可能不太一样。下面…...

VB车辆管理系统SQL设计与实现
摘 要 随着信息时代的到来,信息高速公路的兴起,全球信息化进入了一个新的发展时期。人们越来越认识到计算机强大的信息模块处理功能,使之成为信息产业的基础和支柱。 我国经济的快速发展,汽车已经成为人们不可缺少的交通工具。对于拥有大量车辆的机关企事业来说,车辆的…...

java 泛型
概述 泛型在java中有很重要的地位,在面向对象编程及各种设计模式中有非常广泛的应用。 泛型,就是类型参数。 一提到参数,最熟悉的就是定义方法时有形参,然后调用此方法时传递实参。 那么类型参数理解呢? 顾名思义&…...

git 查看/配置 local/global 用户名称和用户邮箱
1、--local: 本地设置(仅对当前仓库有效) git config --local user.name “你的名称” git config --local user.email “你的邮箱” 2、--global 全局设置(对当前用户的所有仓库有效) git config --global user.name “你的名称…...

无涯教程-分类算法 - 简介
分类可以定义为根据观测值或给定数据点预测类别的过程。分类的输出可以采用"黑色"或"白色"或"垃圾邮件"或"非垃圾邮件"的形式。 在数学上,分类是从输入变量(X)到输出变量(Y)近似映射函数(f)的任务,它属于有监督…...
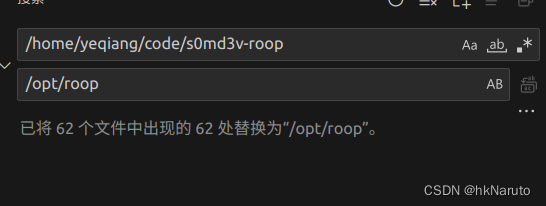
python venv 打包,更换路径后,仍然读取到旧路径 ,最好别换路径,采用docker封装起来
机械盘路径 /home/yeqiang/code/xxx 移动到 /opt/xxx 编辑/opt/xxx/venv/bin/activate VIRTUAL_ENV"/home/yeqiang/code/xxx/venv" 改为 VIRTUAL_ENV"/opt/xxx/venv" 下面还有这么多,参考: (venv) yeqiangyeqiang-MS-7B23:/…...
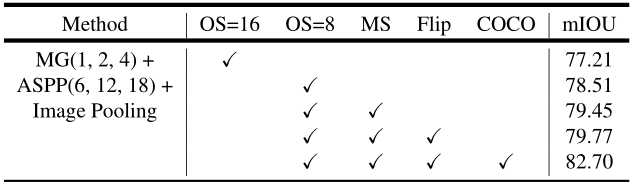
MATLAB算法实战应用案例精讲-【自然语言处理】语义分割模型-DeepLabV3
目录 1、DeepLab系列简介 1.1.DeepLabV1 1.1.1创新点: 1.1.2. 动机: 1.1.3. 应对策略: 1.2.DeepLabV2 1.2.1.创新点: 1.2.2.动机 1.2.3. 应对策略: 1.3.DeepLabV3 1.3.1创新点: 1.3.2. 动机&am…...

road to master
零、学习计划 数据库相关 索引 我以为我对数据库索引很了解,直到我遇到了阿里面试官 - 知乎 (zhihu.com)给我一分钟,让你彻底明白MySQL聚簇索引和非聚簇索引 - 知乎 (zhihu.com)聚集索引(聚类索引)与非聚集索引(非聚类…...
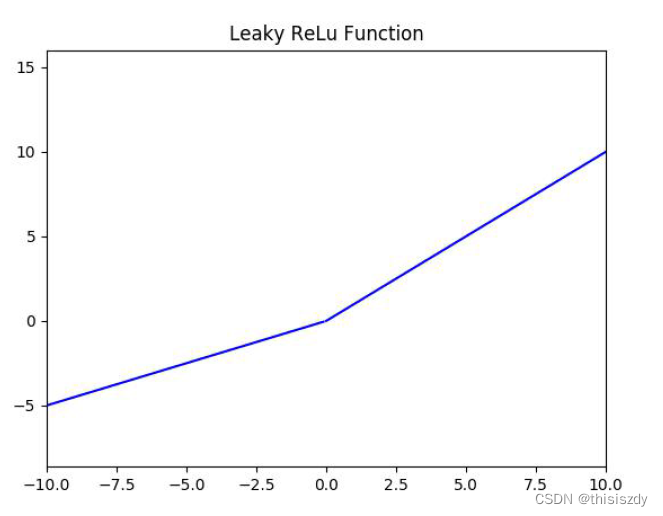
<深度学习基础> 激活函数
为什么需要激活函数?激活函数的作用? 激活函数可以引入非线性因素,可以学习到复杂的任务或函数。如果不使用激活函数,则输出信号仅是一个简单的线性函数。线性函数一个一级多项式,线性方程的复杂度有限,从…...

评价指标BLUE了解
BLEU (Bilingual Evaluation Understudy,双语评估基准)是一组度量机器翻译和自然语言生成模型性能的评估指标。BLEU指标是由IBM公司提出的一种模型评估方法,以便在机器翻译领域中开发更好的翻译模型。BLEU指标根据生成的句子与人工参考句子之间的词、短语…...

5G网关如何提升智慧乡村农业生产效率
得益于我国持续推进5G建设,截至今年5月,我国5G基站总数已达284.4万个,覆盖全国所有地级市、县城城区和9成以上的乡镇镇区,实现“镇镇通5G”,全面覆盖了从城市到农村的延伸。 依托5G网络的技术优势,智慧乡村…...
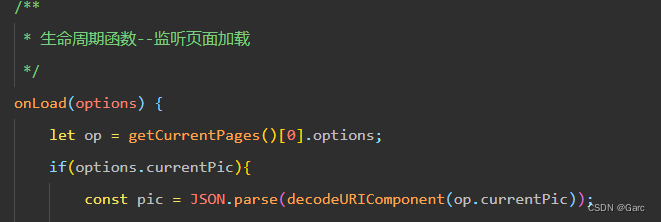
微信小程序分享后真机参数获取不到和部分参数不能获取问题问题解决
微信小程序的很多API,都是BUG,近期开发小程序就遇到了分享后开发工具可以获取参数,但是真机怎么都拿不到参数的问题 一、真机参数获取不到问题解决 解决方式: 在onLoad(options) 中。 onLoad方法中一定要有options 这个参数。…...
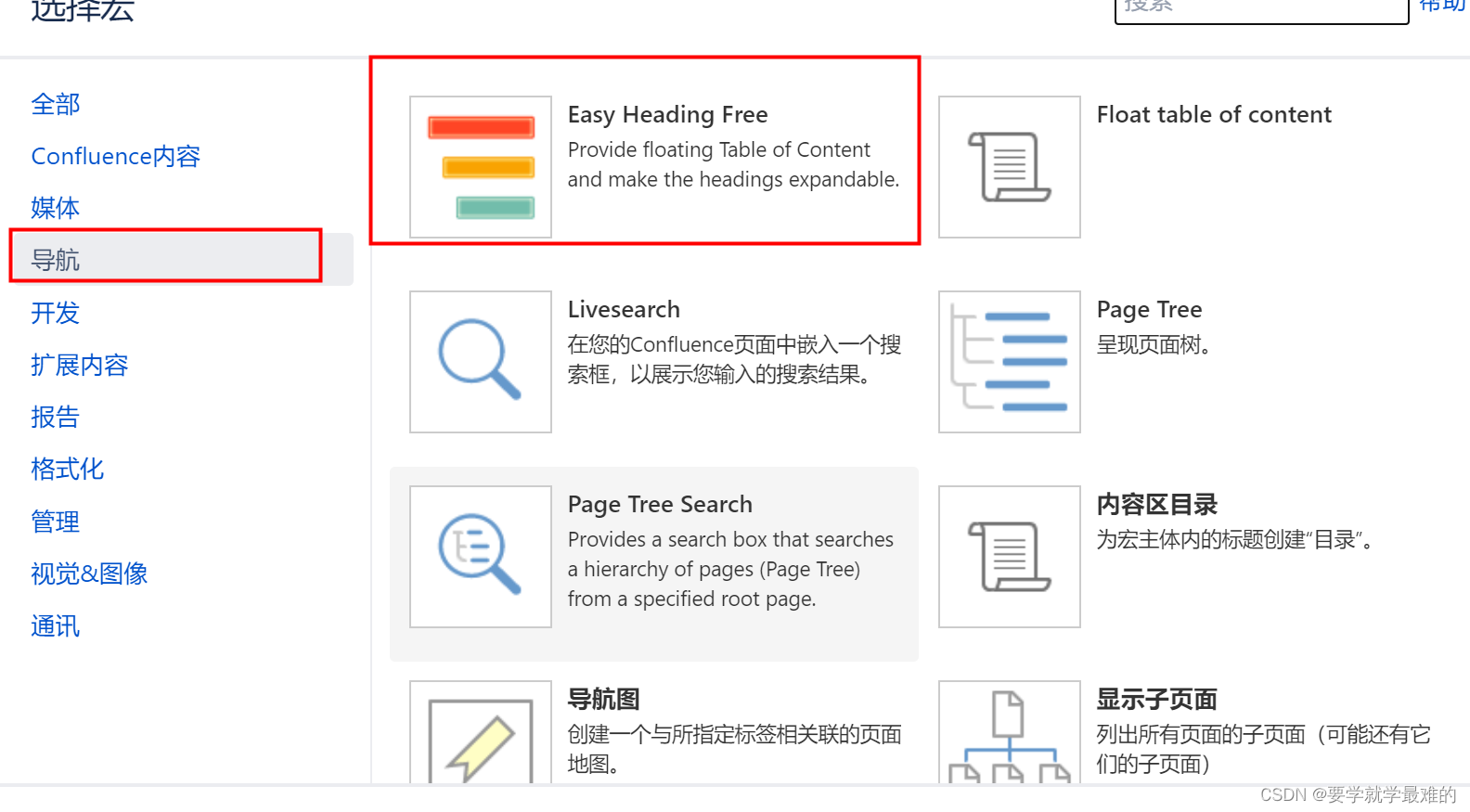
Confluence使用教程(用户篇)
1、如何创建空间 可以把空间理解成一个gitlab仓库,空间之间相互独立,一般建议按照部门(小组的人太少,没必要创建空间)或者按照项目分别创建空间 2、confluence可以创建两种类型的文档:页面和博文 从内容上来…...
网络基础知识socket编程
目录 网络通信概述网络互连模型:OSI 七层模型TCP/IP 四层/五层模型数据的封装与拆封 IP 地址IP 地址的编址方式IP 地址的分类特殊的IP 地址如何判断2 个IP 地址是否在同一个网段内 TCP/IP 协议TCP 协议TCP 协议的特性TCP 报文格式建立TCP 连接:三次握手关…...
基于SpringBoot的员工(人事)管理系统
基于SpringBoot的员工(人事)管理系统 一、系统介绍二、功能展示三.其他系统实现五.获取源码 一、系统介绍 项目名称:基于SPringBoot的员工管理系统 项目架构:B/S架构 开发语言:Java语言 前端技术:BootS…...

【计算机网络】序列化与反序列化
文章目录 1. 如何处理结构化数据?序列化 与 反序列化 2. 实现网络版计算器1. Tcp 套接字的封装——sock.hpp创建套接字——Socket绑定——Bind将套接字设置为监听状态——Listen获取连接——Accept发起连接——Connect 2. 服务器的实现 ——TcpServer.hpp初始化启动…...
Linux内核学习(七)—— 定时器和时间管理(基于Linux 2.6内核)
目录 一、内核中的时间概念 二、节拍率:HZ 实时时钟 系统定时器 三、定时器 系统定时器是一种可编程硬件芯片,能以固定频率产生定时器中断,它所对应的中断处理程序负责更新系统时间,也负责执行需要周期性运行的任务。 一、内…...
常用命令总结)
Tortoise Git(乌龟git)常用命令总结
查看全局和本地 Git 配置 打开命令行终端(如 Git Bash),分别执行以下命令查看全局和本地的 Git 配置信息: git config --global -l git config --local -l确保配置中没有任何与 SSH 相关的设置 移除全局和本地 SSH 相关配置&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
