当前位置： 首页 > news >正文

常用的GPT插件

news 文章来源：https://blog.csdn.net/lovely_yoshino/article/details/132507668 2024/9/22 2:10:51

0.简介

随着chatgpt爆火，这玩意并不对国内用户开放，如果想要使用的话还要需要进行翻墙以及国外手机号才能进行注册。

对于国内来说有很多国内免费的方法，这里就整理一下，方便大家开发

1. 网站类型

下面的网站无需注册即可免费使用，大家打开网站即可使用，而且相应速度是还是比较快的，大家可以测试一下，回答的风格和chatGPT几乎无异。

1.1 chatisfy

这个网站是需要登录的，但是使用使免费的
在这里插入图片描述

1.2 forefront

ForeFrontAI网站是一个提供免费的AI在线聊天机器人服务的平台，支持多种主流模型，包括GPT-3.5、GPT-4、Claude Instant和Claude+。用户可以登录至chat.forefront.ai使用这些模型与聊天机器人进行交互。该网站还允许用户享受已经训练过的各种大型语言模型，并使用迁移学习技术进行定制，以创建适应其独特需求的AI模型
在这里插入图片描述

1.3 astarcloud

这是国内的一个网站，需要从公众号获取访问

在这里插入图片描述

1.4 you

同样的国外网站，作为一个具有全新外观和私密模式的搜索引擎，挑战着 Google 搜索的地位。此外，You.com 雄心勃勃，致力于成为一个 All-In-One 的平台，除了传统搜索功能，还包括其他服务
在这里插入图片描述

1.5 writesonic

AI写作网站，支持gpt3.5和4
在这里插入图片描述

1.6 poe

Poe（可能是指PoE平台）是一个综合性的AI工具平台，用于整合多个人工智能技术，包括Sage、GPT-4、Claude +、Claude instant、ChatGPT3.5、Dragonfly等。它的功能涵盖创新写作、复杂问题解决、编程帮助、娱乐等多个领域。这个平台能够帮助用户构建智能对话系统，提供自动化的客户服务和支持，以及执行其他语音助手和聊天机器人的开发任务。
在这里插入图片描述

1.7 binjie

国内一个网站，目前是访问即可使用的
在这里插入图片描述

1.8 cloud.dify

Dify新对接了一批开源的、国产合规的大模型。如：miniMax、讯飞星火、通义千问、文心一言、chatGLM等以及部署在Replicate、Hugging Face平台上的所有模型！
使用Llama2、ChatGLM、通义千问、讯飞星火、MiniMax、文心一言等模型轻松切换使用，快速构建性能优异且多样化的 AI 应用！
Dify还支持自定义 OpenAI（社区版）、Anthropic（社区版）、Azure OpenAI等模型的服务器域名！
在这里插入图片描述

2. 浏览器插件

2.1 WebChatGPT

WebChatGPT 是一个浏览器插件，使 ChatGPT 能够联网，从而获得最新和准确的信息。这个插件允许 ChatGPT 在生成回答时访问互联网，以提供更相关和实时的答案。用户安装插件后，通过在 ChatGPT 的提示中添加相关网络搜索结果，它增强了 ChatGPT 的功能，使其能够在对话中引用网络信息。这种集成扩展了 ChatGPT 的知识和能力，使其更适用于各种任务，包括查找和提供最新信息、答案和建议。通过 WebChatGPT 插件，用户可以在对话中获取更全面的知识和信息支持。
在这里插入图片描述

2.2 ChatGPT for Google

…详情请参照古月居

相关文章：

常用的GPT插件

0.简介 随着chatgpt爆火，这玩意并不对国内用户开放，如果想要使用的话还要需要进行翻墙以及国外手机号才能进行注册。 对于国内来说有很多国内免费的方法，这里就整理一下，方便大家开发 1. 网站类型 下面的网站无需注册即可免费…...

编程日记 2023/8/30 10:26:18

智慧校园用电安全解决方案

随着科技的不断发展，智慧校园建设逐渐成为了教育行业的一大趋势。在这个过程中，电力系统作为校园基础设施的重要组成部分，其安全、稳定、高效的运行显得尤为重要。下面小编来为大家介绍下智慧校园用电安全解决方案吧! 一、智慧校园电力系统现…...

编程日记 2023/8/30 10:25:17

【教程】DGL中的子图分区函数partition_graph讲解

转载请注明出处：小锋学长生活大爆炸[xfxuezhang.cn] 目录 函数形式 函数作用 函数内容 函数入参 函数返参 使用示例 实际上官方的函数解释中就已经非常详细了。 函数形式 def partition_graph(g, graph_name, num_parts, out_path, num_hops1, part…...

编程日记 2023/8/30 10:24:14

关于layui table回显以及选择下一页时记住上一页数据的问题

代码如下 <div class"layui-form-item"><label class"layui-form-label">选择商品</label><div class"layui-input-inline"><input type"text" name"keyword" id"keyword" placehold…...

编程日记 2023/8/30 10:23:13

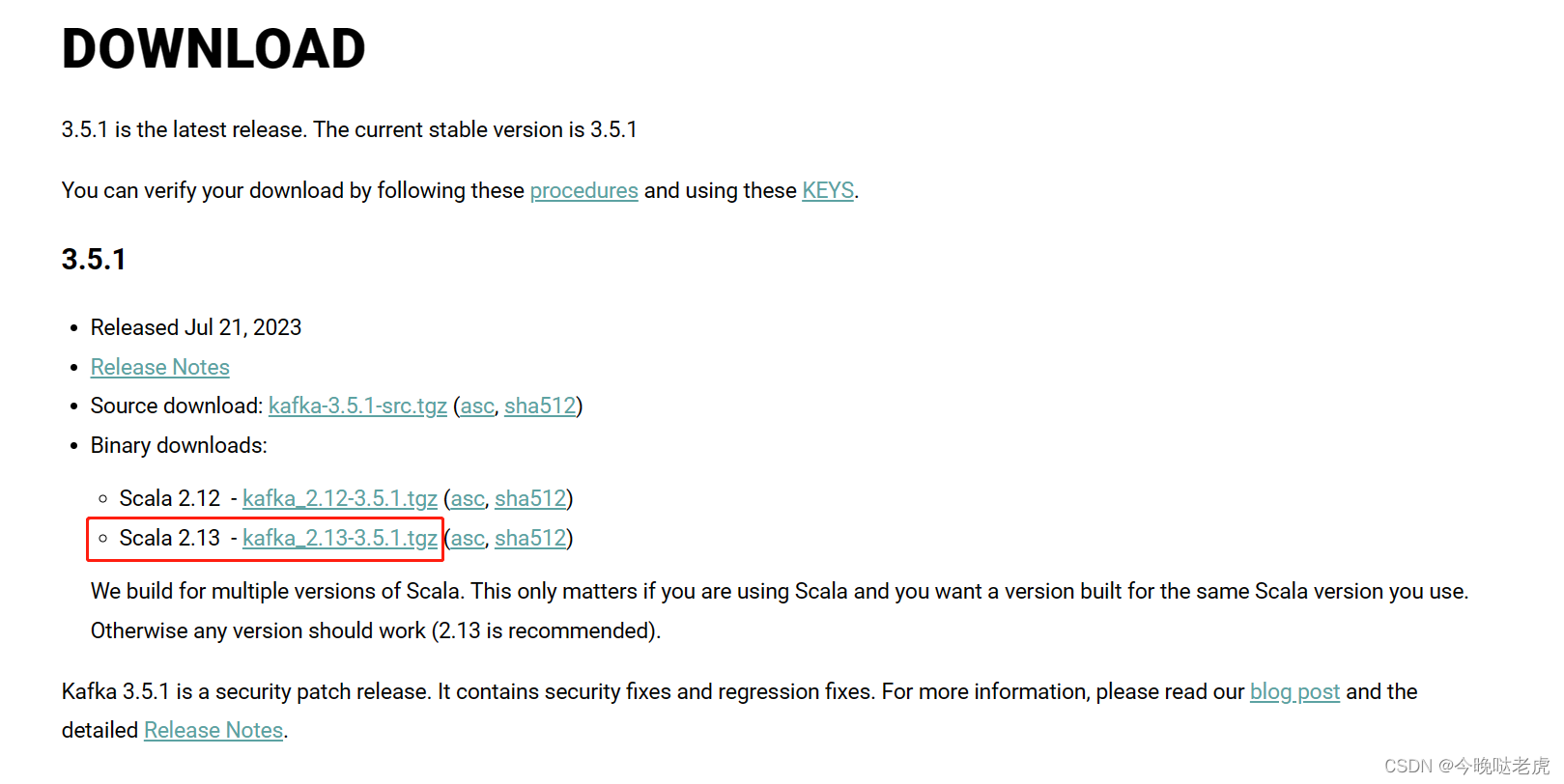
kafka消息系统实战

kafka是什么&#xff1f; 是一种高吞吐量的、分布式、发布、订阅、消息系统 1.导入maven坐标 <dependency><groupId>org.apache.kafka</groupId><artifactId>kafka-clients</artifactId><version>2.4.1</version></dependency&…...

编程日记 2023/8/30 10:22:12

Kafka3.0.0版本——Leader故障处理细节原理

目录 一、服务器信息二、服务器基本信息及相关概念2.1、服务器基本信息2.2、LEO的概念2.3、HW的概念 三、Leader故障处理细节 一、服务器信息 三台服务器 原始服务器名称原始服务器ip节点centos7虚拟机1192.168.136.27broker0centos7虚拟机2192.168.136.28broker1centos7虚拟机…...

编程日记 2023/8/30 10:21:10

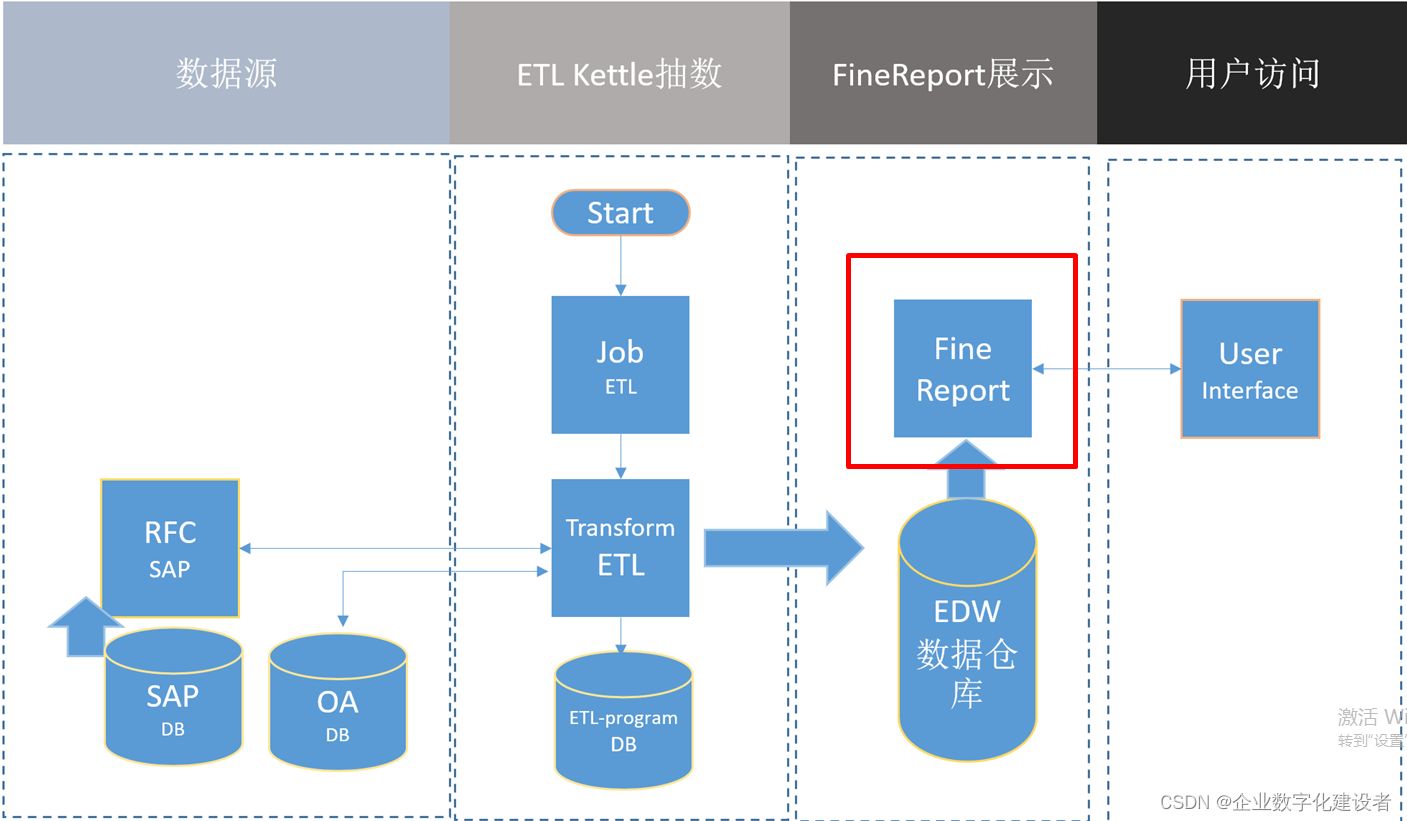
BI系统框架模型

一 技术架构 二 数据源 主数据 &#xff1a;组织|岗位|人员|大区|三大主数据&#xff08;客户、物料、供应商&#xff09;财务主数据&#xff08;科目|成本中心|利润中心|资产&#xff09;|工作中心|工艺路线 业务数据 &#xff1a;线索|业务机会|合同|订单|采购|生产|发…...

编程日记 2023/8/30 10:20:09

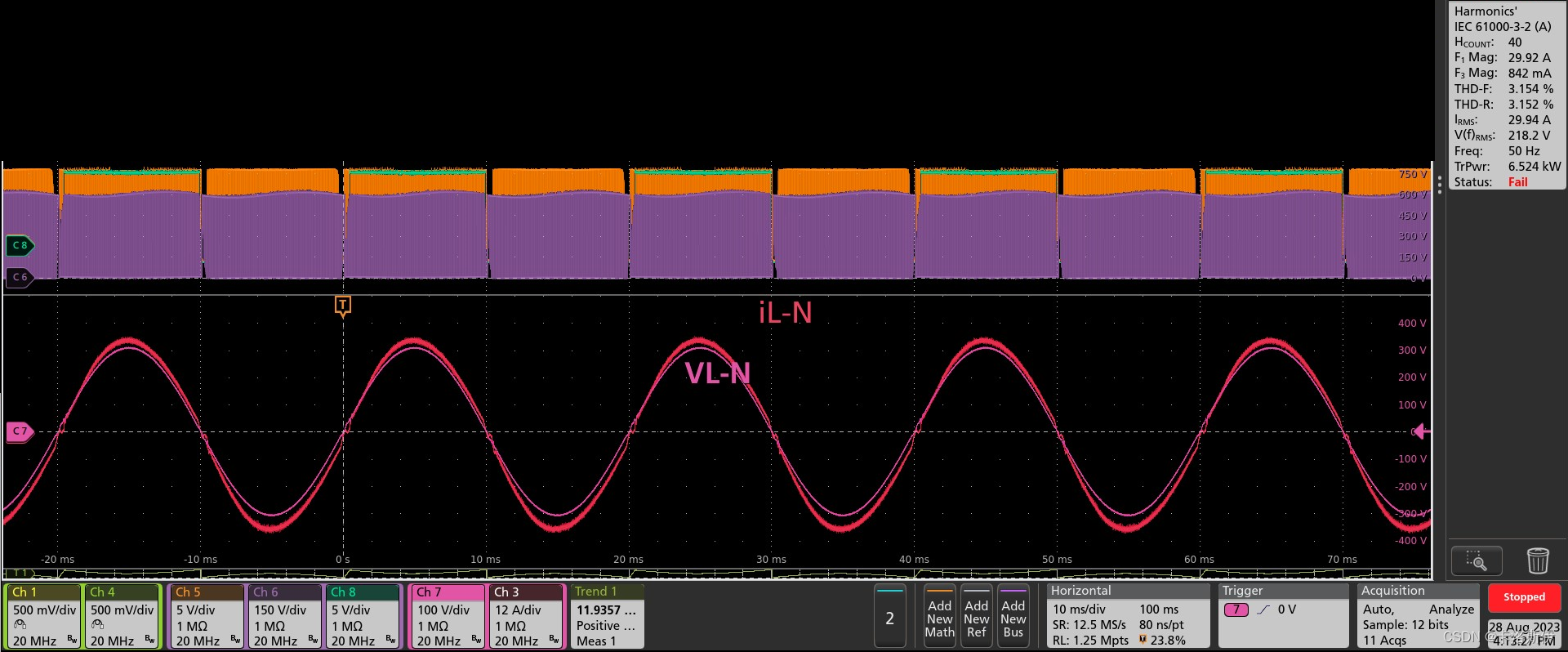
双向交错CCM图腾柱无桥单相PFC学习仿真与实现（3）硬件功能实现

前言 前面介绍了双向交错CCM图腾柱的系统设计仿真实现&#xff0c;仿真很理想 双向交错CCM图腾柱无桥单相PFC学习仿真与实现&#xff08;1&#xff09;系统问题分解_卡洛斯伊的博客-CSDN博客 然后又介绍了SOG锁相环仿真实现的原理 双向交错CCM图腾柱无桥单相PFC学习仿真与实…...

编程日记 2023/8/30 10:19:07

微软用 18 万行 Rust 重写了 Windows 内核

微软正在使用 Rust 编程语言重写其核心 Windows 库。 5 月 11 日——Azure 首席技术官 Mark Russinovich 表示&#xff0c;最新的 Windows 11 Insider Preview 版本是第一个包含内存安全编程语言 Rust 的版本。 “如果你参加了 Win11 Insider 环&#xff0c;你将在 Windows 内…...

编程日记 2023/8/30 10:18:05

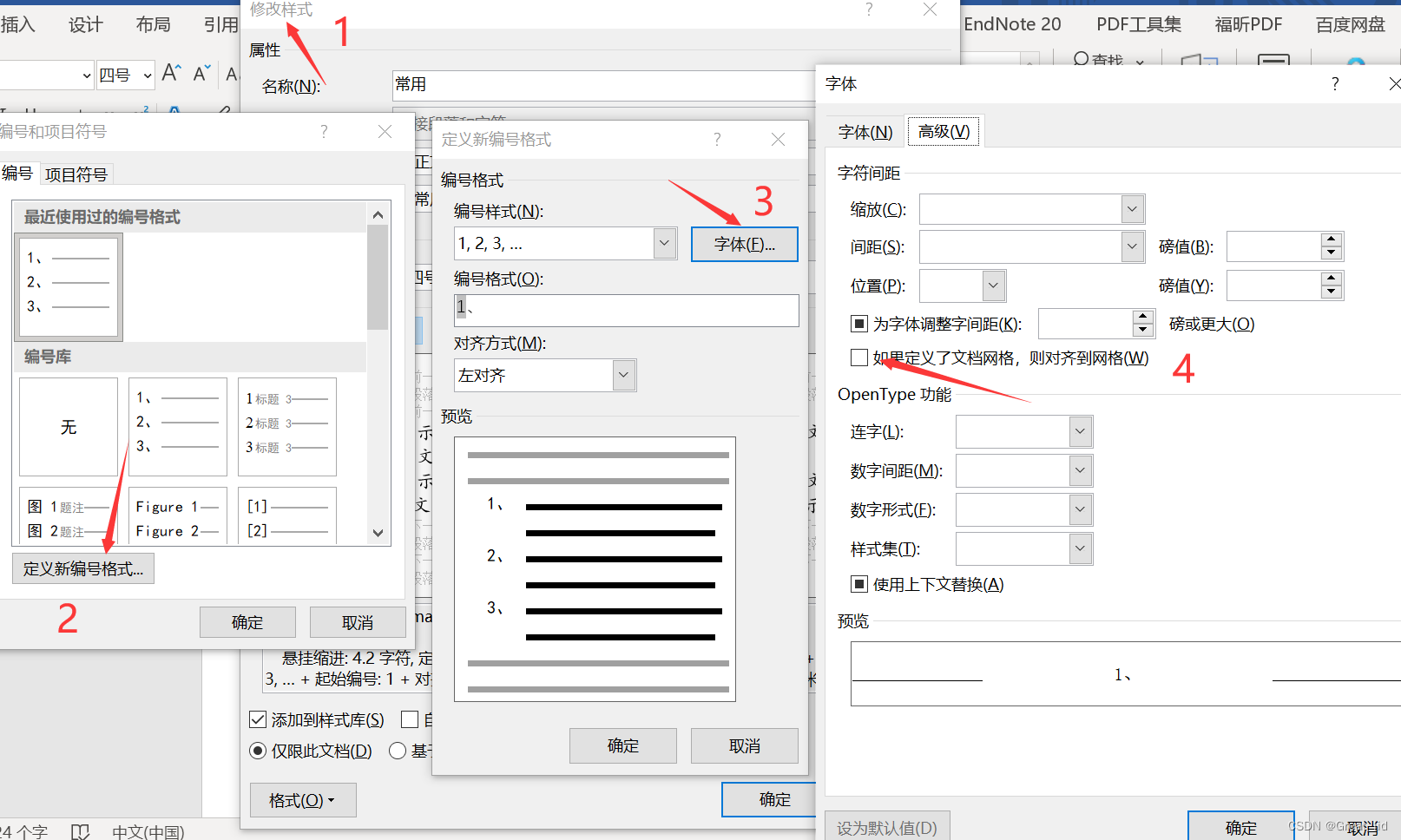
word 调整列表缩进

word 调整列表缩进的一种方法&#xff0c;在试了其他方法无效后&#xff0c;按下图所示顺序处理&#xff0c;编号和文字之间的空白就没那么大了。 即右键word上方样式->点击修改格式->定义新编号格式->字体->取消勾选 “……对齐到网格”->确定...

编程日记 2023/8/30 10:17:04

nginx学习

一、nginx常用版本 Nginx开源版&#xff1a; http://nginx.org/ nginx plus商业版本&#xff08;好像功能支持更多&#xff09; https://www.nginx.com/ openresty &#xff08;免费&#xff0c;用的也是这个&#xff09; https://openresty.org/cn/ Tengine https://tengine.…...

编程日记 2023/8/30 10:16:02

python+TensorFlow实现人脸识别智能小程序的项目（包含TensorFlow版本与Pytorch版本）（一）

pythonTensorFlow实现人脸识别智能小程序的项目&#xff08;包含TensorFlow版本与Pytorch版本&#xff09;&#xff08;一&#xff09; 一&#xff1a;TensorFlow基础知识内容部分&#xff08;简明扼要&#xff0c;快速适应&#xff09;1、下载Cifar10数据集&#xff0c;并进行…...

编程日记 2023/8/30 10:15:01

ChatGPT怎么用于政府和公共服务？

将ChatGPT用于政府和公共服务领域是一种创新的应用方式&#xff0c;可以改善政府与公众之间的互动&#xff0c;提升公共服务的效率和质量。ChatGPT作为一个自然语言处理模型&#xff0c;可以在政府信息传递、公共参与、服务支持等方面发挥积极作用。以下将详细探讨ChatGPT如何用…...

编程日记 2023/8/30 10:13:59

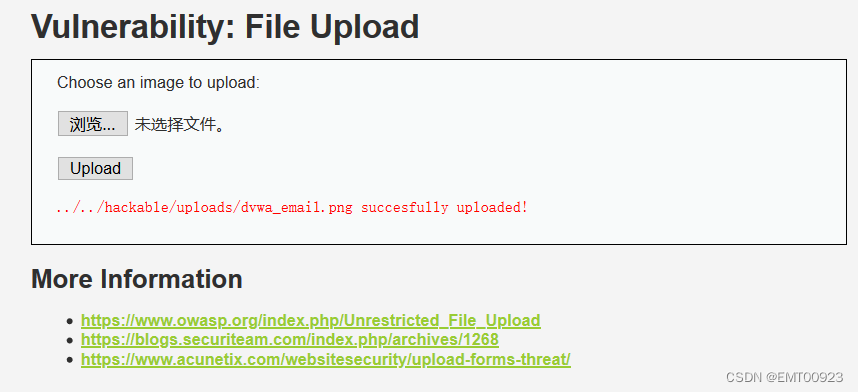
dvwa文件上传通关及代码分析

文章目录 low等级medium等级high等级Impossible等级 low等级 查看源码&#xff1a; <?phpif( isset( $_POST[ Upload ] ) ) {// Where are we going to be writing to?$target_path DVWA_WEB_PAGE_TO_ROOT . "hackable/uploads/";$target_path . basename( …...

编程日记 2023/8/30 10:12:57

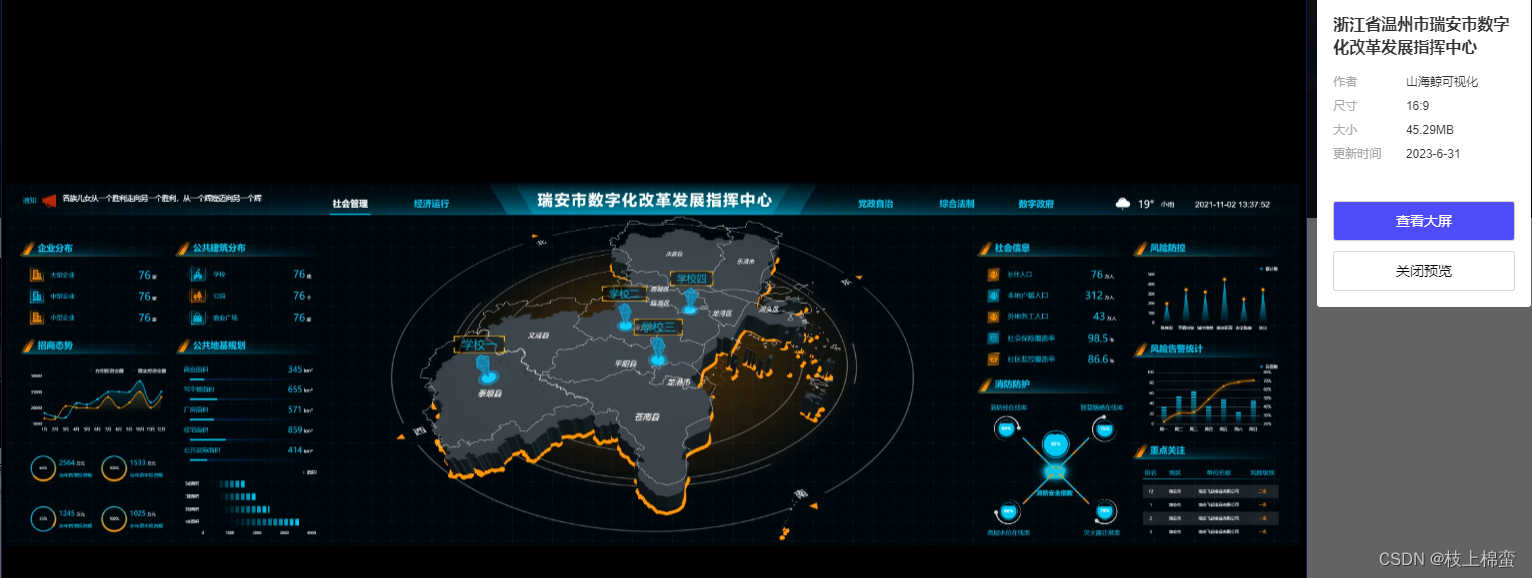
数字孪生：重塑政府决策与公共服务

在之前的文章中为大家分享了数字孪生在很多行业的应用场景&#xff0c;本文和大家一起探讨一下数字孪生在政务管理方面能有哪些应用&#xff0c;以及其对公共服务提供的积极影响。 1&#xff09;城市规划方面 数字孪生技术可用于模拟城市的发展和规划。政府可以建立城市的虚拟…...

编程日记 2023/8/30 10:11:55

Leetcode:【448. 找到所有数组中消失的数字】题解

题目 给你一个含 n 个整数的数组 nums &#xff0c;其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字&#xff0c;并以数组的形式返回结果。 难度&#xff1a;简单 题目链接&#xff1a;448. 找到所有数组中消失的数字 示例1 输入&…...

编程日记 2023/8/30 10:10:54

2023年中，量子计算产业现状——

2023年上半年&#xff0c;量子计算&#xff08;QC&#xff09;领域取得了一系列重要进展和突破&#xff0c;显示出量子计算技术的快速发展和商业应用的不断拓展。在iCV TAnk近期发表的一篇报告中&#xff0c;团队从制度进步、产业生态、投融资形势、总结与展望四个方面对量子计…...

编程日记 2023/8/30 10:09:53

微信小程序智慧流调微信小程序设计与实现

摘 要 自从2020年新冠疫情爆发以来&#xff0c;对全国人民的健康和全国各地区的经济发展都带来了很大的影响&#xff0c;并且新冠肺炎对各个领域带来的影响还未完全消除。近三年以来&#xff0c;全国各地区多次爆发新的疫情&#xff0c;导致许多人被隔离&#xff0c;也导致全国…...

编程日记 2023/8/30 10:08:52

分布式集群框架——有关zookeeper的面试考点

3.掌握Zookeeper的概念 当涉及到大规模分布式系统的协调和管理时&#xff0c;Zookeeper是一个非常重要的工具。 1. 分布式协调服务&#xff1a;Zookeeper是一个分布式协调服务&#xff0c;它提供了一个高可用和高性能的环境&#xff0c;用于协调和同步分布式系统中的各个节点…...

编程日记 2023/8/30 10:07:51

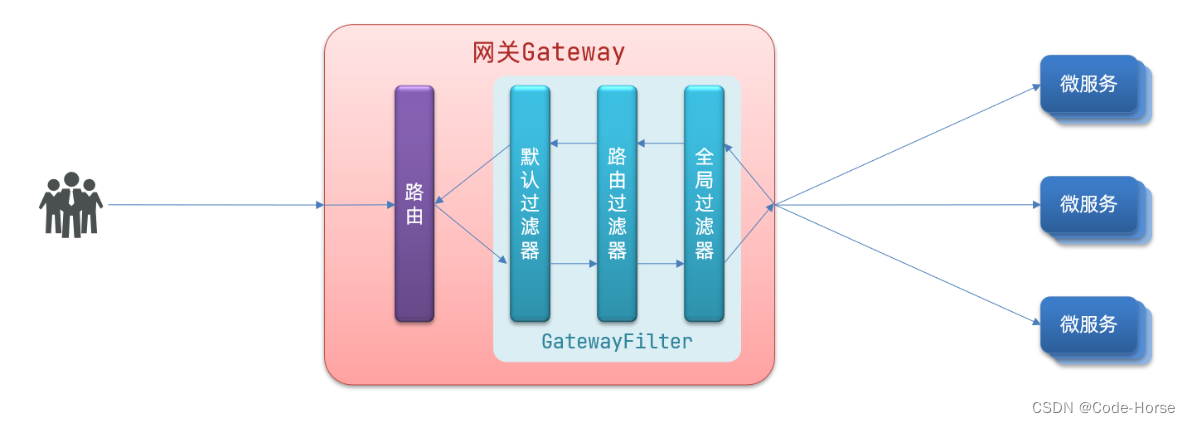
Spring Cloud Gateway的快速使用

环境前置搭建Nacos&#xff1a;点击跳转 Spring Cloud Gateway Docs 新建gateway网关模块 pom.xml导入依赖 <!-- 网关 --> <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-gateway</artifact…...

编程日记 2023/8/30 10:06:49

VSCode-C++环境配置+Cmake

文章目录 一、环境配置二、Win10 Cmake 一、环境配置 转载链接 二、Win10 Cmake 创建CMakeLists.txt cmake_minimum_required(VERSION 3.26) project(graph_algorithm)set(CMAKE_CXX_STANDARD 17)add_executable(main main.cppshared_variable.cpp )cmake . -G "MinGW…...

编程日记 2023/8/30 10:05:48

python爬虫14：总结

python爬虫14&#xff1a;总结 前言 ​ python实现网络爬虫非常简单&#xff0c;只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点&#xff0c;方便以后复习。 申明 ​ 本系列所涉及的代码仅用于个人研究与讨论&#xff0c;并不会对网站产生不好…...

编程日记 2023/8/30 10:04:47

扩散模型实战（八）：微调扩散模型

推荐阅读列表&#xff1a; 扩散模型实战&#xff08;一&#xff09;&#xff1a;基本原理介绍 扩散模型实战&#xff08;二&#xff09;&#xff1a;扩散模型的发展 扩散模型实战&#xff08;三&#xff09;&#xff1a;扩散模型的应用 扩散模型实战&#xff08;四&#xf…...

编程日记 2023/8/30 10:03:45

Android 全局控件属性设置

一 使用需求&#xff1a; 如 设置全局字体、全局文本属性设置 二 实现方式&#xff1a; 在App使用的主题中&#xff0c;添加属性及属性值 如给所有的文本设置属性,注释部分作用是设置应用全局字体 <style name"Theme.AppDemo" parent"Base.Theme.AppDemo&q…...

编程日记 2023/8/30 10:02:43

下面是实践百度飞桨上面的pm2.5分类项目_logistic regression相关

part1:数据的引入&#xff0c;和前一个linear regression基本是一样 part2:数据解析——也就是数据的“规格化” 首先&#xff0c;打算用dataMat[]和labelMat[]数据存储feature和label&#xff0c;并且文件变量fr 然后&#xff0c;是这个for line in fr.readlines()循环&#…...

编程日记 2023/8/30 10:01:42

阿里云误删Python后域yum报错解决方案

阿里云误删Python后域yum报错解决方案 1:找回所有依赖 这里依赖可能很多,也搞不清楚有哪些,建议买一台临时服务器,系统选择跟你当前的系统一致的,配置选最低就行 2:登录临时服务器,创建临时文件夹 mkdir /usr/local/yum-fix cd /usr/local/yum-fix3:查找并下载所有云依赖 r…...

编程日记 2023/8/30 10:00:41

unordered-------Hash

✅<1>主页&#xff1a;我的代码爱吃辣&#x1f4c3;<2>知识讲解&#xff1a;数据结构——哈希表☂️<3>开发环境&#xff1a;Visual Studio 2022&#x1f4ac;<4>前言&#xff1a;哈希是一种映射的思想&#xff0c;哈希表即使利用这种思想&#xff0c;…...

编程日记 2023/8/30 9:59:38

数据仓库总结

1.为什么要做数仓建模 数据仓库建模的目标是通过建模的方法更好的组织、存储数据&#xff0c;以便在性能、成本、效率和数据质量之间找到最佳平衡点。 当有了适合业务和基础数据存储环境的模型&#xff08;良好的数据模型&#xff09;&#xff0c;那么大数据就能获得以下好处&…...

编程日记 2023/8/30 9:58:36

hadoop学习：mapreduce入门案例二：统计学生成绩

这里相较于 wordcount&#xff0c;新的知识点在于学生实体类的编写以及使用 数据信息&#xff1a; 1. Student 实体类 import org.apache.hadoop.io.WritableComparable;import java.io.DataInput; import java.io.DataOutput; import java.io.IOException;public class Stude…...

编程日记 2023/8/30 9:57:35

自学TypeScript-基础、编译、类型

自学TypeScript-基础、编译、类型 TS 编译为 JS类型支持类型注解基础类型typeof 运算符高级类型class 类构造函数和实例方法继承可见性只读 类型兼容性交叉类型泛型泛型约束多个泛型泛型接口泛型类泛型工具 索引签名类型映射类型索引查询(访问)类型 类型声明文件 TypeScript 是…...

编程日记 2023/8/30 9:56:33

nginx配置https

1.安装nginx 安装完成后检查 nginx -V2.申请证书与上传 阿里云申请免费的证书 然后上传到某个目录 3.修改nginx配置 #user nobody; worker_processes 1;#error_log logs/error.log; #error_log logs/error.log notice; #error_log logs/error.log info;#pid …...

编程日记 2023/8/30 9:55:33

windows Etcd的安装与使用

一、简介 etcd是一个分布式一致性键值存储&#xff0c;其主要用于分布式系统的共享配置和服务发现。 etcd由Go语言编写 二、下载并安装 1.下载地址&#xff1a; https://github.com/coreos/etcd/releases 解压后的目录如下&#xff1a;其中etcd.exe是服务端&#xff0c;e…...

编程日记 2023/8/30 9:54:31

【py】为什么用 import tkinter 不能运行

为什么用 import tkinter 不能运行 ━━━━━━━━━━━━━━━━━━━━━━ 要显示一个信息框&#xff0c;为什么用 import tkinter 不能运行&#xff0c;改成from tkinter import messagebox 就可以运行了&#xff1f; 可能是因为您的代码中只使用了 messagebox 这个模…...

编程日记 2023/8/30 9:53:29

【深度学习】实验04 交叉验证

文章目录 交叉验证划分自定义划分K折交叉验证留一交叉验证留p交叉验证随机排列交叉验证分层K折交叉验证分层随机交叉验证 分割组 k-fold分割留一组分割留 P 组分割随机分割时间序列分割 交叉验证 # 导入相关库# 交叉验证所需函数 from sklearn.model_selection import train_t…...

编程日记 2023/8/30 9:52:27

whisper语音识别部署及WER评价

1.whisper部署 详细过程可以参照&#xff1a;&#x1f3e0; 创建项目文件夹 mkdir whisper cd whisper conda创建虚拟环境 conda create -n py310 python3.10 -c conda-forge -y 安装pytorch pip install --pre torch torchvision torchaudio --extra-index-url 下载whisper p…...

编程日记 2023/8/30 9:51:27

java太卷了，怎么办？

忧虑&#xff1a; 马上就到30岁了&#xff0c;最近对于自己职业生涯的规划甚是焦虑。在网站论坛上&#xff0c;可谓是哀鸿遍野&#xff0c;大家纷纷叙述着自己被裁后求职的艰辛路程&#xff0c;这更加加深了我的忧虑&#xff0c;于是在各大论坛开始“求医问药”&#xff0c;想…...

编程日记 2023/8/30 9:50:25

android多屏触摸相关的详解方案-安卓framework开发手机车载车机系统开发课程

背景 直播免费视频课程地址&#xff1a;https://www.bilibili.com/video/BV1hN4y1R7t2/ 在做双屏相关需求开发过程中&#xff0c;经常会有对两个屏幕都要求可以正确触摸的场景。但是目前我们模拟器默认创建的双屏其实是没有办法进行触摸的 修改方案1 静态修改方案 使用命令…...

编程日记 2023/8/30 9:49:23

微信小程序 实时日志

目录 实时日志 背景 如何使用 如何查看日志 注意事项 实时日志 背景 为帮助小程序开发者快捷地排查小程序漏洞、定位问题&#xff0c;我们推出了实时日志功能。从基础库2.7.1开始&#xff0c;开发者可通过提供的接口打印日志&#xff0c;日志汇聚并实时上报到小程序后台…...

编程日记 2023/8/30 9:48:20

Spring AOP基于注解方式实现和细节

目录 一、Spring AOP底层技术 二、初步实现AOP编程 三、获取切点详细信息 四、 切点表达式语法 五、重用&#xff08;提取&#xff09;切点表达式 一、Spring AOP底层技术 SpringAop的核心在于动态代理&#xff0c;那么在SpringAop的底层的技术是依靠了什么技术呢&#x…...

编程日记 2023/8/30 9:47:19

CVPR2023论文及代码合集来啦~

以下内容由马拉AI整理汇总。 下载&#xff1a;点我跳转。 狂肝200小时的良心制作&#xff0c;529篇最新CVPR2023论文及其Code&#xff0c;汇总成册&#xff0c;制作成《CVPR 2023论文代码检索目录》&#xff0c;包括以下方向&#xff1a; 1、2D目标检测 2、视频目标检测 3、…...

编程日记 2023/8/30 9:46:18

基于ETLCloud的自定义规则调用第三方jar包实现繁体中文转为简体中文

背景 前面曾体验过通过零代码、可视化、拖拉拽的方式快速完成了从 MySQL 到 ClickHouse 的数据迁移&#xff0c;但是在实际生产环境&#xff0c;我们在迁移到目标库之前还需要做一些过滤和转换工作&#xff1b;比如&#xff0c;在诗词数据迁移后&#xff0c;发现原来 MySQL 中…...

编程日记 2023/8/30 9:45:14

TDesign在按钮上加入图标组件

在实际开发中 我们经常会遇到例如 添加或者查询 我们需要在按钮上加入图标的操作 TDesign自然也有预备这样的操作 首先我们打开文档看到图标 例如 我们先用某些图标 就可以点开下面的代码 可以看到 我们的图标大部分都是直接用tdesign-icons-vue 导入他的组件就可以了 而我…...

编程日记 2023/8/30 9:44:13

Linux 终端命令行 产品介绍

Linux命令手册内置570多个Linux 命令&#xff0c;内容包含 Linux 命令手册。 【软件功能】&#xff1a; 文件传输 bye、ftp、ftpcount、ftpshut、ftpwho、ncftp、tftp、uucico、uucp、uupick、uuto、scp备份压缩 ar、bunzip2、bzip2、bzip2recover、compress、cpio、dump、gun…...

编程日记 2023/8/30 9:43:11

计算机毕设 基于深度学习的植物识别算法 - cnn opencv python

文章目录 0 前言1 课题背景2 具体实现3 数据收集和处理3 MobileNetV2网络4 损失函数softmax 交叉熵4.1 softmax函数4.2 交叉熵损失函数 5 优化器SGD6 最后 0 前言 &#x1f525; 这两年开始毕业设计和毕业答辩的要求和难度不断提升&#xff0c;传统的毕设题目缺少创新和亮点&a…...

编程日记 2023/8/30 9:42:08

【STM32】学习笔记-江科大

【STM32】学习笔记-江科大 1、STM32F103C8T6的GPIO口输出 2、GPIO口输出 GPIO&#xff08;General Purpose Input Output&#xff09;通用输入输出口可配置为8种输入输出模式引脚电平&#xff1a;0V~3.3V&#xff0c;部分引脚可容忍5V输出模式下可控制端口输出高低电平&#…...

编程日记 2023/8/30 9:41:06

Doris架构中包含哪些技术？

Doris主要整合了Google Mesa(数据模型)&#xff0c;Apache Impala(MPP Query Engine)和Apache ORCFile (存储格式&#xff0c;编码和压缩)的技术。 为什么要将这三种技术整合? Mesa可以满足我们许多存储需求的需求&#xff0c;但是Mesa本身不提供SQL查询引擎。 Impala是一个…...

编程日记 2023/8/30 9:40:04

《vue3实战》通过indexOf方法实现电影评价系统的模糊查询功能

目录 前言 一、indexOf是什么&#xff1f;indexOf有什么作用&#xff1f; 含义&#xff1a; 作用&#xff1a; 二、功能实现 这段是查询过程中过滤筛选功能的代码部分: 分析&#xff1a; 这段是查询用户和性别功能的代码部分&#xff1a; 分析&#xff1a; 三、最终效…...

编程日记 2023/8/30 9:39:03

java对时间序列每x秒进行分组

问题&#xff1a;将一个时间序列每5秒分一组&#xff0c;返回嵌套的list&#xff1b; 原理&#xff1a;int除int会得到一个int&#xff08;也就是损失精度&#xff09; 输入&#xff1a;排序后的list&#xff0c;每几秒分组值 private static List<List<Long>> get…...

编程日记 2023/8/30 9:38:02

八月更新 | CI 构建计划触发机制升级、制品扫描 SBOM 分析功能上线！

点击链接了解详情 这个八月&#xff0c;腾讯云 CODING DevOps 对持续集成、制品管理、项目协同、平台权限等多个产品模块进行了升级改进&#xff0c;为用户提供更灵活便捷的使用体验。以下是 CODING 新功能速递&#xff0c;快来看看是否有您期待已久的功能特性&#xff1a; 01…...

编程日记 2023/8/30 9:37:01

Spring核心配置步骤-完全基于XML的配置

Spring框架的核心配置涉及多个方面&#xff0c;包括依赖注入&#xff08;DI&#xff09;、面向切面编程&#xff08;AOP&#xff09;等。以下是一般情况下配置Spring应用程序的核心步骤&#xff1a; 1. **引入Spring依赖&#xff1a;** 在项目的构建工具&#xff08;如Maven、…...

编程日记 2023/8/30 9:35:59