数字孪生:重塑政府决策与公共服务
在之前的文章中为大家分享了数字孪生在很多行业的应用场景,本文和大家一起探讨一下数字孪生在政务管理方面能有哪些应用,以及其对公共服务提供的积极影响。
1)城市规划方面
数字孪生技术可用于模拟城市的发展和规划。政府可以建立城市的虚拟模型,通过模拟不同规划方案的影响,预测城市未来的发展趋势。这有助于合理规划城市基础设施、交通系统、环保措施等,实现城市可持续发展。
2)决策支持方面
政府决策往往涉及复杂的数据和变量。数字孪生技术可以为政府提供实时的虚拟模型,用于模拟不同政策决策的效果。决策者可以在虚拟环境中测试各种方案,从而做出更准确、明智的决策。
3)公共安全预测方面
数字孪生技术可用于公共安全领域,模拟自然灾害、交通事故、犯罪发生等情况。政府可以通过模拟预测风险,制定更有效的应急计划和预防措施,提高公众安全水平。
4)教育与健康管理方面
政府可以利用数字孪生技术模拟教育和健康管理情境。在教育领域,政府可以优化学校布局、师资配置等,提高教育质量。在健康领域,政府可以预测疾病传播趋势,优化医疗资源分配。
5)公众参与与透明度方面
数字孪生技术可以为公众提供更多参与政务决策的机会。政府可以创建虚拟场景,让公众在虚拟环境中体验政策效果,提供反馈意见。这有助于增加政府与公众之间的互动和透明度。
总之,数字孪生技术正逐渐成为政务管理的一大利器。通过模拟、预测、优化等方式,政府可以更好地应对各种挑战,提升政务效率,实现更智能、更可持续的政务管理。数字孪生为政府机构带来了更广阔的发展空间,也为公众提供了更优质的公共服务。
相关文章:

数字孪生:重塑政府决策与公共服务
在之前的文章中为大家分享了数字孪生在很多行业的应用场景,本文和大家一起探讨一下数字孪生在政务管理方面能有哪些应用,以及其对公共服务提供的积极影响。 1)城市规划方面 数字孪生技术可用于模拟城市的发展和规划。政府可以建立城市的虚拟…...

Leetcode:【448. 找到所有数组中消失的数字】题解
题目 给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 难度:简单 题目链接:448. 找到所有数组中消失的数字 示例1 输入&…...

2023年中,量子计算产业现状——
2023年上半年,量子计算(QC)领域取得了一系列重要进展和突破,显示出量子计算技术的快速发展和商业应用的不断拓展。在iCV TAnk近期发表的一篇报告中,团队从制度进步、产业生态、投融资形势、总结与展望四个方面对量子计…...

微信小程序智慧流调微信小程序设计与实现
摘 要 自从2020年新冠疫情爆发以来,对全国人民的健康和全国各地区的经济发展都带来了很大的影响,并且新冠肺炎对各个领域带来的影响还未完全消除。近三年以来,全国各地区多次爆发新的疫情,导致许多人被隔离,也导致全国…...

分布式集群框架——有关zookeeper的面试考点
3.掌握Zookeeper的概念 当涉及到大规模分布式系统的协调和管理时,Zookeeper是一个非常重要的工具。 1. 分布式协调服务:Zookeeper是一个分布式协调服务,它提供了一个高可用和高性能的环境,用于协调和同步分布式系统中的各个节点…...
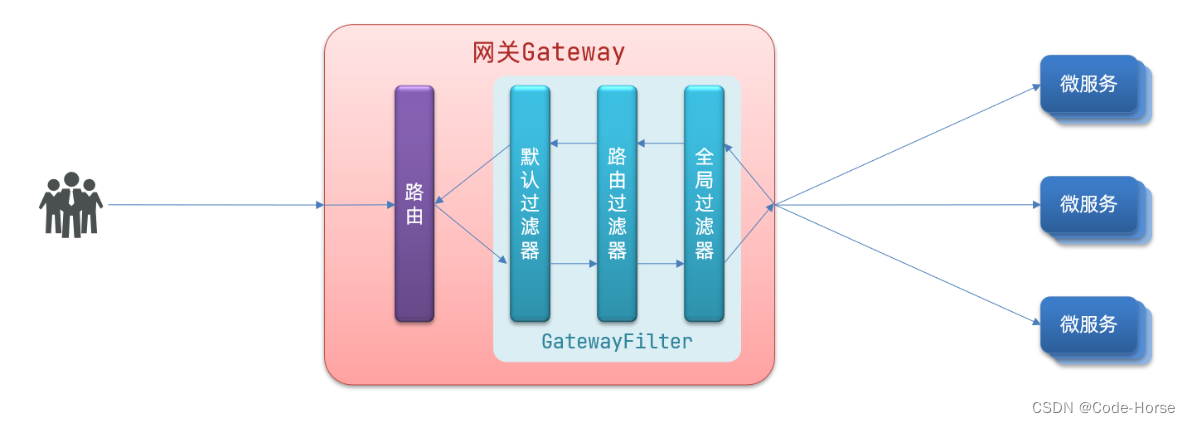
Spring Cloud Gateway的快速使用
环境前置搭建Nacos:点击跳转 Spring Cloud Gateway Docs 新建gateway网关模块 pom.xml导入依赖 <!-- 网关 --> <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-gateway</artifact…...

VSCode-C++环境配置+Cmake
文章目录 一、环境配置二、Win10 Cmake 一、环境配置 转载链接 二、Win10 Cmake 创建CMakeLists.txt cmake_minimum_required(VERSION 3.26) project(graph_algorithm)set(CMAKE_CXX_STANDARD 17)add_executable(main main.cppshared_variable.cpp )cmake . -G "MinGW…...

python爬虫14:总结
python爬虫14:总结 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网站产生不好…...

扩散模型实战(八):微调扩散模型
推荐阅读列表: 扩散模型实战(一):基本原理介绍 扩散模型实战(二):扩散模型的发展 扩散模型实战(三):扩散模型的应用 扩散模型实战(四…...

Android 全局控件属性设置
一 使用需求: 如 设置全局字体、全局文本属性设置 二 实现方式: 在App使用的主题中,添加属性及属性值 如给所有的文本设置属性,注释部分作用是设置应用全局字体 <style name"Theme.AppDemo" parent"Base.Theme.AppDemo&q…...

下面是实践百度飞桨上面的pm2.5分类项目_logistic regression相关
part1:数据的引入,和前一个linear regression基本是一样 part2:数据解析——也就是数据的“规格化” 首先,打算用dataMat[]和labelMat[]数据存储feature和label,并且文件变量fr 然后,是这个for line in fr.readlines()循环&#…...

阿里云误删Python后域yum报错解决方案
阿里云误删Python后域yum报错解决方案 1:找回所有依赖 这里依赖可能很多,也搞不清楚有哪些,建议买一台临时服务器,系统选择跟你当前的系统一致的,配置选最低就行 2:登录临时服务器,创建临时文件夹 mkdir /usr/local/yum-fix cd /usr/local/yum-fix3:查找并下载所有云依赖 r…...
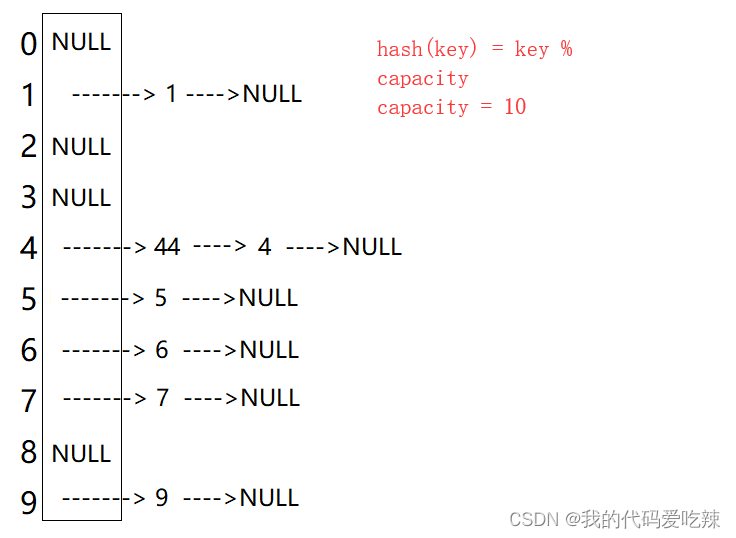
unordered-------Hash
✅<1>主页:我的代码爱吃辣📃<2>知识讲解:数据结构——哈希表☂️<3>开发环境:Visual Studio 2022💬<4>前言:哈希是一种映射的思想,哈希表即使利用这种思想,…...

数据仓库总结
1.为什么要做数仓建模 数据仓库建模的目标是通过建模的方法更好的组织、存储数据,以便在性能、成本、效率和数据质量之间找到最佳平衡点。 当有了适合业务和基础数据存储环境的模型(良好的数据模型),那么大数据就能获得以下好处&…...
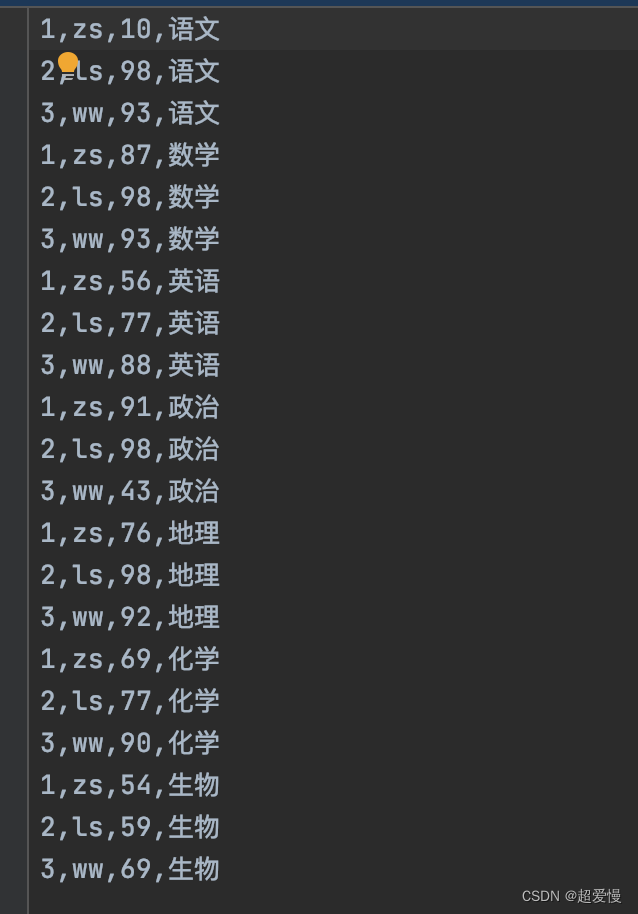
hadoop学习:mapreduce入门案例二:统计学生成绩
这里相较于 wordcount,新的知识点在于学生实体类的编写以及使用 数据信息: 1. Student 实体类 import org.apache.hadoop.io.WritableComparable;import java.io.DataInput; import java.io.DataOutput; import java.io.IOException;public class Stude…...

自学TypeScript-基础、编译、类型
自学TypeScript-基础、编译、类型 TS 编译为 JS类型支持类型注解基础类型typeof 运算符高级类型class 类构造函数和实例方法继承可见性只读 类型兼容性交叉类型泛型泛型约束多个泛型泛型接口泛型类泛型工具 索引签名类型映射类型索引查询(访问)类型 类型声明文件 TypeScript 是…...

nginx配置https
1.安装nginx 安装完成后检查 nginx -V2.申请证书与上传 阿里云申请免费的证书 然后上传到某个目录 3.修改nginx配置 #user nobody; worker_processes 1;#error_log logs/error.log; #error_log logs/error.log notice; #error_log logs/error.log info;#pid …...
windows Etcd的安装与使用
一、简介 etcd是一个分布式一致性键值存储,其主要用于分布式系统的共享配置和服务发现。 etcd由Go语言编写 二、下载并安装 1.下载地址: https://github.com/coreos/etcd/releases 解压后的目录如下:其中etcd.exe是服务端,e…...

【py】为什么用 import tkinter 不能运行
为什么用 import tkinter 不能运行 ━━━━━━━━━━━━━━━━━━━━━━ 要显示一个信息框,为什么用 import tkinter 不能运行,改成from tkinter import messagebox 就可以运行了? 可能是因为您的代码中只使用了 messagebox 这个模…...

【深度学习】实验04 交叉验证
文章目录 交叉验证划分自定义划分K折交叉验证留一交叉验证留p交叉验证随机排列交叉验证分层K折交叉验证分层随机交叉验证 分割组 k-fold分割留一组分割留 P 组分割随机分割时间序列分割 交叉验证 # 导入相关库# 交叉验证所需函数 from sklearn.model_selection import train_t…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
