机器学习笔记之最优化理论与方法(一)最优化问题概述
机器学习笔记之最优化理论与方法——最优化问题概述
- 引言
- 什么是最优化问题
- 最优化问题的基本形式
- 最优化问题的分类
- 各分类最优化问题的数学表达
- 约束优化VS无约束优化
- 线性规划VS非线性规划
- 连续优化VS离散优化
- 单目标优化VS多目标优化
引言
从本节开始,将对最优化理论与方法进行简单认识。
什么是最优化问题
无论是最优化理论还是最优化方法,讨论的对象都是最优化问题。
关于最优化问题的一种简单描述:最优化问题本质上属于决策问题。
- 例如路径选择问题:确定达到目的地最佳路径的计量标准。其中问题的目标可能包含:路径距离最短、行驶费用最少等等。
- 再例如车辆调度问题:通过制定行车路线,使车辆再满足一定约束条件下,有序通过一系列装货点和卸货点,以达到如最短路程、耗时最少、费用最小等目标。
也就是说,我们需要从若干个可执行策略中挑出一个/若干个策略,从而使待处理问题的目标达到最优。
具体的说,一个最优化问题会包含如下三个部分:
- 决策变量:在执行策略过程中需要做决定的信息。例如车辆调度问题中的路径选择。
- 目标函数:在制定策略之前,需要明确要优化的目标。而目标函数是对目标的计量方式进行表达。目标函数可能不止一个,不同角度的目标可能对应不同的目标函数。例如上述车辆调度问题中的最短路程、耗时最小、费用最小。它们都可以作为目标,从而制定相应的目标函数。
- 约束条件:由可行策略组成的集合,通常使用等式/不等式进行描述。
最优化问题的基本形式
关于最优化问题的数学符号表达如下:
{ min or max f ( x ) x = ( x 1 , ⋯ , x p ) T s.t. { g i ( x ) ≤ 0 i = 1 , 2 , ⋯ , m h j ( x ) = 0 j = 1 , 2 , ⋯ , l x ∈ X \begin{cases} \begin{aligned} & \min \text{ or } \max f(x) \quad x = (x_1,\cdots,x_p)^T \\ & \text{s.t. } \begin{cases} g_i(x) \leq 0 \quad i=1,2,\cdots,m \\ h_j(x) = 0 \quad j = 1,2,\cdots,l \\ \end{cases} \\ & x \in \mathcal X \end{aligned} \end{cases} ⎩ ⎨ ⎧min or maxf(x)x=(x1,⋯,xp)Ts.t. {gi(x)≤0i=1,2,⋯,mhj(x)=0j=1,2,⋯,lx∈X
-
其中 x i ( i = 1 , 2 , ⋯ , p ) x_i(i=1,2,\cdots,p) xi(i=1,2,⋯,p)是决策变量;而 x x x则表示由若干决策变量组成的决策向量。
-
而目标函数作为目标的计量方式,它必然与决策向量相关。它具体描述为关于决策向量的一个函数:
也就是说,一旦得到一个/一组确定的决策x x x,必然会得到目标相应的计量结果f ( x ) f(x) f(x)。
f ( x ) = f ( x 1 , x 2 , ⋯ , x p ) f(x) = f(x_1,x_2,\cdots,x_p) f(x)=f(x1,x2,⋯,xp)
而 min f ( x ) \min f(x) minf(x)与 max f ( x ) \max f(x) maxf(x)分别表示对目标函数最小化或最大化,根据实际情况而定。 -
而 g i ( x ) g_i(x) gi(x)同样是关于决策向量 x x x的一个函数。在执行决策的过程中,可能存在相关资源的限制。而 g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0则是一种不等式相关的条件限制,称作不等式约束。
同理, h j ( x ) = 0 h_j(x) = 0 hj(x)=0则是一种等式相关的条件限制,被称作等式约束。
这里的i , j i,j i,j描述不等式/等式约束的编号,对应的m , l m,l m,l描述不等式/等式约束的数量。 -
而 x ∈ X x \in \mathcal X x∈X则表示决策向量 x x x的定义域空间 X \mathcal X X。通常情况下,对 X \mathcal X X的描述比较简单、宽泛。例如: X ∈ R p \mathcal X \in \mathbb R^p X∈Rp,即 x x x是一个实数向量; X ∈ R + p \mathcal X \in \mathbb R_+^p X∈R+p,即 x x x是一个非负的实数向量; X ∈ Z p \mathcal X \in \mathcal Z^p X∈Zp,即 x x x是一个整数向量等等。根据具体的实际问题具体设置。
虽然 X \mathcal X X描述了 x x x的基本性质,但并不代表 X \mathcal X X内的所有值 x x x都可以取到。观察如下集合:
S = { x ∈ X ∣ g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m ; h j ( x ) = 0 , j = 1 , 2 , ⋯ , l } \mathcal S = \{x \in \mathcal X \mid g_i(x) \leq 0,i=1,2,\cdots,m;h_j(x) = 0,j=1,2,\cdots,l\} S={x∈X∣gi(x)≤0,i=1,2,⋯,m;hj(x)=0,j=1,2,⋯,l}
这个集合 S \mathcal S S同样是描述决策向量 x x x的集合,但不同于 X \mathcal X X的是,它被称作上述优化问题的可行域。也就是说,决策向量 x x x可在可行域 S \mathcal S S内进行取值。而 x ∈ S x \in \mathcal S x∈S则表示在可行域范围 S \mathcal S S内的一种决策/一个决策向量 x x x,也被称作一个可行解。
最优化问题的分类
关于上述最优化问题的基本形式/一般形式,可以通过不同角度对最优化问题进行分类:
这仅是几种常见分类~
- 如果最优化问题中没有约束条件(等式 h j ( x ) = 0 h_j(x) = 0 hj(x)=0、不等式 g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0约束),被称作无约束优化;相反,被称作约束优化;
- 如果最优化问题中目标函数/约束条件中存在非线性函数,被称作非线性优化;反之,被称作线性优化;
其中线性优化也即运筹学中的线性规划。 - 关于决策向量 x x x,对其内部随机变量的离散/连续性,将其划分为离散优化/连续优化。
也可以通过可行域 S \mathcal S S内决策向量 x x x的数量进行表述。如果数量可数,则是离散优化;反之,则是连续优化。 - 如果最优化问题中同时存在多个目标函数,被称作多目标优化;反之,被称作单目标优化。
各分类最优化问题的数学表达
约束优化VS无约束优化
关于无约束优化的数学符号表示如下:
min f ( x ) \min f(x) minf(x)
虽然在整个运筹学中,最优化问题来自于实际的生产问题——在制定决策(目标函数)过程中,该决策必然伴随着约束条件。
例如上面描述的资源限制、成本、人力、投资等等实际问题中的限制。
从而基于这些限制建模产生的优化问题通常情况下不会是无约束优化问题。但一些情况下:我们可以通过一些策略将约束优化问题转化为无约束优化问题的形式,并加以求解。例如一个约束优化示例表示如下:
{ min f ( x ) s.t. g ( x ) = 0 \begin{cases} \min f(x) \\ \text{s.t. } g(x) = 0 \end{cases} {minf(x)s.t. g(x)=0
并将其转化为如下优化问题的表达形式:
min { f ( x ) + M ⋅ [ g ( x ) ] 2 } \min \left\{ f(x) + \mathcal M \cdot [g(x)]^2 \right\} min{f(x)+M⋅[g(x)]2}
其中 M \mathcal M M取一个充分大的数值。之所以将 M \mathcal M M取值充分大的目的是:
- 在保证 f ( x ) f(x) f(x)达到最小之前,必然要先保证 g ( x ) ⇒ 0 g(x) \Rightarrow 0 g(x)⇒0,因为如果 g ( x ) ≠ 0 g(x) \neq 0 g(x)=0,那么 [ g ( x ) ] 2 [g(x)]^2 [g(x)]2必然是一个正值,该结果与 M \mathcal M M相乘后必然是一个较大的量,从而该结果必然与要优化的目标相悖。
可以通过这种方法,可以将上述示例的约束优化问题转化为对应的无约束优化问题。一些常见的无约束优化方法如:
这里没有添加链接的部分后续补上~
- 最速下降法(梯度下降法)
- 牛顿法
- 共轭梯度法
而上面这种将约束优化转化为无约束优化的约束优化方法被称作罚函数法。在后续进行逐步介绍。
线性规划VS非线性规划
关于线性规划标准形式的数学符号描述(示例)表示如下:
{ min C T x s.t. A x = b ; x ≥ 0 \begin{cases} \min \mathcal C^T x \\ \text{s.t. } \mathcal A x = b;x \geq 0 \end{cases} {minCTxs.t. Ax=b;x≥0
针对求解线性规划问题的常用方法是单纯形算法 ( Simplex Algorithm ) (\text{Simplex Algorithm}) (Simplex Algorithm)。它的思路可简单描述为:
线性规划方法这里仅作科普使用~
- 算法支撑:如果线性规划问题的最优解存在,则一定可以在其可行域的顶点中找到。
- 具体思路:先找出可行域内的一个顶点,根据一定规则判断其是否最优;
- 如果上述顶点不是最优,则转换到与该顶点相邻的另一顶点,并使目标函数达到最优;直到找到某最优解为止。
关于非线性规划(示例)—— Markowitz \text{Markowitz} Markowitz均值-方差模型:
-
假设投资市场中有 n n n个可投资的风险资产 ( Risk Assets ) (\text{Risk Assets}) (Risk Assets):对当前时刻的价格已知,但不知其未来时刻的价格;
-
其中编号为 i ( i = 1 , 2 , ⋯ , n ) i(i=1,2,\cdots,n) i(i=1,2,⋯,n)的资产,它的收益率表示为 R i \mathcal R_i Ri;作为投资者,在资产 i i i上的投资比重(单位:百分比)记作 x i x_i xi,其中 x i ∈ [ 0 , 1 ] x_i \in [0,1] xi∈[0,1];对应地,投资者对所有风险资产均存在一个投资比重,从而得到一个投资比重向量(决策向量) X \mathcal X X:
X = ( x 1 , x 2 , ⋯ , x n ) T ∑ i = 1 n x i = 1 \mathcal X = (x_1,x_2,\cdots,x_n)^T \quad \sum_{i=1}^n x_i = 1 X=(x1,x2,⋯,xn)Ti=1∑nxi=1 -
关于决策向量 X \mathcal X X对应的收益量是关于 X \mathcal X X的一个函数,并表示为如下形式:
R ( X ) = R 1 ⋅ x 1 + R 2 ⋅ x 2 + ⋯ + R n ⋅ x n \mathcal R(\mathcal X) = \mathcal R_1 \cdot x_1 + \mathcal R_2 \cdot x_2 + \cdots +\mathcal R_n \cdot x_n R(X)=R1⋅x1+R2⋅x2+⋯+Rn⋅xn
由于这些资产是风险资产,那么关于各资产的收益率 R i ( i = 1 , 2 , ⋯ , n ) \mathcal R_i(i=1,2,\cdots,n) Ri(i=1,2,⋯,n)自然是不确定的。因而 R i \mathcal R_i Ri是一个随机变量;在 Markowitz \text{Markowitz} Markowitz均值-方差模型中对收益描述表示为收益量期望 E [ R ( X ) ] \mathbb E[\mathcal R(\mathcal X)] E[R(X)]的形式:
记E [ R i ] = r i ( i = 1 , 2 , ⋯ , n ) \mathbb E[\mathcal R_i] = r_i(i=1,2,\cdots,n) E[Ri]=ri(i=1,2,⋯,n)。
E [ R ( X ) ] = E [ R 1 ⋅ x 1 + R 2 ⋅ x 2 + ⋯ + R n ⋅ x n ] = r 1 ⋅ x 1 + r 2 ⋅ x 2 + ⋯ + r n ⋅ x n = ∑ i = 1 n r i ⋅ x i \begin{aligned} \mathbb E[\mathcal R(\mathcal X)] & = \mathbb E[\mathcal R_1 \cdot x_1 + \mathcal R_2 \cdot x_2 + \cdots + \mathcal R_n \cdot x_n] \\ & = r_1 \cdot x_1 + r_2 \cdot x_2 + \cdots + r_n \cdot x_n \\ & = \sum_{i=1}^n r_i \cdot x_i \end{aligned} E[R(X)]=E[R1⋅x1+R2⋅x2+⋯+Rn⋅xn]=r1⋅x1+r2⋅x2+⋯+rn⋅xn=i=1∑nri⋅xi
由于收益的不确定性越大,风险越大。因此 Markowitz \text{Markowitz} Markowitz均值-方差模型关于对风险的描述表示为收益量方差 Var [ R ( X ) ] \text{Var}[\mathcal R(\mathcal X)] Var[R(X)]:衡量随机变量 R ( X ) \mathcal R(\mathcal X) R(X)关于期望结果 E [ R ( X ) ] \mathbb E[\mathcal R(\mathcal X)] E[R(X)]附近波动程度的考量:
其中Cov ( R i , R j ) \text{Cov}(\mathcal R_i,\mathcal R_j) Cov(Ri,Rj)表示随机变量R i , R j \mathcal R_i,\mathcal R_j Ri,Rj的协方差结果。记作σ i j \sigma_{ij} σij。
Var [ R ( X ) ] = ∑ i = 1 n ∑ j = 1 n Cov ( R i , R j ) x i x j = ∑ i = 1 n ∑ j = 1 n σ i j ⋅ x i x j \text{Var}[\mathcal R(\mathcal X)] = \sum_{i=1}^n\sum_{j=1}^n \text{Cov}(\mathcal R_i,\mathcal R_j) x_i x_j = \sum_{i=1}^n\sum_{j=1}^n \sigma_{ij} \cdot x_ix_j Var[R(X)]=i=1∑nj=1∑nCov(Ri,Rj)xixj=i=1∑nj=1∑nσij⋅xixj -
从而对应的最优化问题描述表示如下:
{ max ∑ i = 1 n r i ⋅ x i min ∑ i = 1 n ∑ j = 1 n σ i j ⋅ x i x j \begin{cases} \begin{aligned} & \max \sum_{i=1}^n r_i\cdot x_i \\ & \min \sum_{i=1}^n \sum_{j=1}^n \sigma_{ij} \cdot x_ix_j \end{aligned} \end{cases} ⎩ ⎨ ⎧maxi=1∑nri⋅ximini=1∑nj=1∑nσij⋅xixj
针对上述问题,一种建模方式是:在给定收益量范围的条件下,使风险达到最小:
其中 Γ \Gamma Γ描述给定收益量范围的下界~
{ min ∑ i = 1 n ∑ j = 1 n σ i j ⋅ x i x j s.t. { ∑ i = 1 n r i ⋅ x i ≥ Γ ∑ i = 1 n x i = 1 X ≥ 0 \begin{cases} \begin{aligned} & \min \sum_{i=1}^n \sum_{j=1}^n \sigma_{ij} \cdot x_i x_j \\ & \text{s.t. } \begin{cases} \sum_{i=1}^n r_i \cdot x_i \geq \Gamma \\ \sum_{i=1}^n x_i = 1 \\ \mathcal X \geq 0 \end{cases} \end{aligned} \end{cases} ⎩ ⎨ ⎧mini=1∑nj=1∑nσij⋅xixjs.t. ⎩ ⎨ ⎧∑i=1nri⋅xi≥Γ∑i=1nxi=1X≥0
很明显,虽然约束条件均是线性约束;但目标函数明显是二次的、非线性的。关于上述问题的建模方式不止一种,很容易能够联想到:在给定风险接受范围的条件下,使收益达到最大:
同理,这里的Δ \Delta Δ描述风险接受范围的上界~无论上面还是下面,都可以称作‘均值-方差模型’Mean-Variance \text{Mean-Variance} Mean-Variance。不管是目标函数还是约束条件中存在非线性函数,它们都称作非线性优化问题。
{ max ∑ i = 1 n r i ⋅ x i s.t. { ∑ i = 1 n ∑ j = 1 n σ i j ⋅ x i x j ≤ Δ ∑ i = 1 n x i = 1 X ≥ 0 \begin{cases} \begin{aligned} & \max \sum_{i=1}^n r_i \cdot x_i \\ & \text{s.t. } \begin{cases} \sum_{i=1}^n \sum_{j=1}^n \sigma_{ij} \cdot x_ix_j \leq \Delta \\ \sum_{i=1}^n x_i = 1 \\ \mathcal X \geq 0 \end{cases} \end{aligned} \end{cases} ⎩ ⎨ ⎧maxi=1∑nri⋅xis.t. ⎩ ⎨ ⎧∑i=1n∑j=1nσij⋅xixj≤Δ∑i=1nxi=1X≥0
连续优化VS离散优化
这里依然以上述的均值-方差模型为例,关于决策变量 x i ( i = 1 , 2 , ⋯ , n ) x_i(i=1,2,\cdots,n) xi(i=1,2,⋯,n)的取值 ∈ [ 0 , 1 ] \in [0,1] ∈[0,1],也就是说,该范围内的任意值均有意义。因而该优化也是连续优化;
如果在均值-方差模型约束条件的基础上,增加额外的约束条件:将风险资产的投资数量限制在 m m m个 ( m < n ) (m < n) (m<n),其余条件以及目标函数均不变。对应建模结果如下:
可以利用指示函数 I ( ⋅ ) \mathbb I(\cdot) I(⋅)对该约束条件进行描述 ⇒ I ( x i ) = { 1 if x i > 0 0 Otherwise \Rightarrow \mathbb I(x_i) = \begin{cases} 1 \quad \text{if }x_i > 0 \\ 0 \quad \text{Otherwise} \end{cases} ⇒I(xi)={1if xi>00Otherwise
{ min ∑ i = 1 n ∑ j = 1 n σ i j ⋅ x i x j s.t. { ∑ i = 1 n r i ⋅ x i ≥ Γ ∑ i = 1 n x i = 1 X ≥ 0 ∑ i = 1 n I ( x i ) ≤ m \begin{cases} \begin{aligned} & \min \sum_{i=1}^n \sum_{j=1}^n \sigma_{ij} \cdot x_i x_j \\ & \text{s.t. } \begin{cases} \sum_{i=1}^n r_i \cdot x_i \geq \Gamma \\ \sum_{i=1}^n x_i = 1 \\ \mathcal X \geq 0 \\ \sum_{i=1}^n \mathbb I(x_i) \leq m \end{cases} \end{aligned} \end{cases} ⎩ ⎨ ⎧mini=1∑nj=1∑nσij⋅xixjs.t. ⎩ ⎨ ⎧∑i=1nri⋅xi≥Γ∑i=1nxi=1X≥0∑i=1nI(xi)≤m
很明显:要从 n n n个风险资产中离散地选择 m m m个结果,这是明显的离散优化,并且是整数规划。
单目标优化VS多目标优化
依然可以使用 Markowitz \text{Markowitz} Markowitz均值-方差模型为例,关于它的最优化问题:
{ max ∑ i = 1 n r i ⋅ x i min ∑ i = 1 n ∑ j = 1 n σ i j ⋅ x i x j \begin{cases} \begin{aligned} & \max \sum_{i=1}^n r_i\cdot x_i \\ & \min \sum_{i=1}^n \sum_{j=1}^n \sigma_{ij} \cdot x_ix_j \end{aligned} \end{cases} ⎩ ⎨ ⎧maxi=1∑nri⋅ximini=1∑nj=1∑nσij⋅xixj
明显可以理解为:包含两个目标函数的多目标优化;关于多目标优化的处理方式:
- 按照非线性规划中的处理方式:将其中一个目标函数保留,其他目标函数转化为约束条件;
- 将多目标优化转化为单目标优化。即:多个目标函数整合成一个目标函数。例如:给各目标函数赋予权重:
通过负号将两个目标函数的优化方向归一;通过权重τ \tau τ控制两个目标函数的比重。
min { τ ⋅ [ ∑ i = 1 n ∑ j = 1 n σ i j ⋅ x i x j ] − ∑ i = 1 n r i ⋅ x i } \min \left\{\tau \cdot \left[\sum_{i=1}^n \sum_{j=1}^n \sigma_{ij} \cdot x_i x_j\right] - \sum_{i=1}^n r_i \cdot x_i\right\} min{τ⋅[i=1∑nj=1∑nσij⋅xixj]−i=1∑nri⋅xi}
相关参考:
最优化理论与方法-第一讲:最优化问题概述
相关文章:
最优化问题概述)
机器学习笔记之最优化理论与方法(一)最优化问题概述
机器学习笔记之最优化理论与方法——最优化问题概述 引言什么是最优化问题最优化问题的基本形式最优化问题的分类各分类最优化问题的数学表达约束优化VS无约束优化线性规划VS非线性规划连续优化VS离散优化单目标优化VS多目标优化 引言 从本节开始,将对最优化理论与…...

【ES5新特性一】 严格模式语法变化、全局的JSON对象、编码和解码的方法
前言 ECMAScript 和 JavaScript 的关系 一个常见的问题是,ECMAScript 和 JavaScript 到底是什么关系? 要讲清楚这个问题,需要回顾历史。1996 年 11 月,JavaScript 的创造者 Netscape 公司,决定将 JavaScript 提交给标准…...
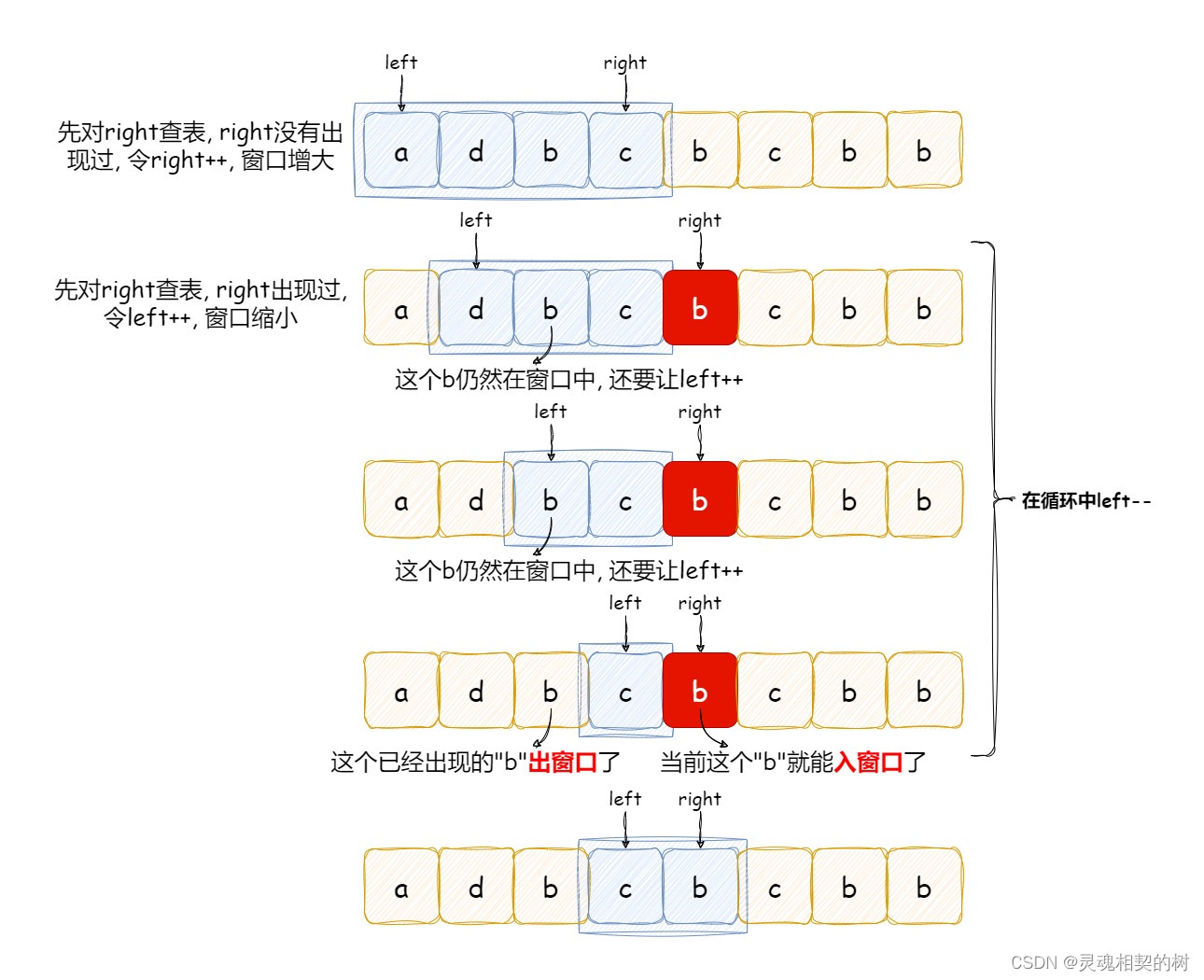
Java【手撕滑动窗口】LeetCode 3. “无重复字符的最长子串“, 图文详解思路分析 + 代码
文章目录 前言一、长度最小子数组1, 题目2, 思路分析3, 代码 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等 📗 Java数据结构: 顺序表, 链…...

学习哈哈哈哈
# 零、学习计划 * 数据库相关 * 索引 * [我以为我对数据库索引很了解,直到我遇到了阿里面试官 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/107487215) * [给我一分钟,让你彻底明白MySQL聚簇索引和非聚簇索引 - 知乎 (zhihu.com)](ht…...

05-基础例程5
基础例程5 1、超声波测距 实验介绍 HC-SR04超声波传感器是一款测量距离的传感器。其原理是利用声波在遇到障碍物反射接收结合声波在空气中传播的速度计算的得出。 外观 管脚功能的定义 VCC:供电电源;Trig:触发信号;Echo&a…...

双基证券:预计未来还会有更多政策来吸引增量资金
双基证券表示,8月27日,活泼资本商场五大方针出台:证券交易印花税折半征收;阶段性收紧IPO节奏;上市房企再融资不受破发、破净和亏本限制;标准控股股东与实际操控人减持行为;融资保证金最低份额由…...

前端:html实现页面切换、顶部标签栏,类似于浏览器的顶部标签栏(完整版)
效果 代码 <!DOCTYPE html> <html><head><style>/* 左侧超链接列表 */.link {display: block;padding: 8px;background-color: #f2f2f2;cursor: pointer;}/* 顶部标签栏 */#tabsContainer {width:98%;display: flex;align-items: center;overflow-x: …...

强化自主可控,润开鸿发布基于RISC-V架构的开源鸿蒙终端新品
2023 RISC-V中国峰会于8月23日至25日在北京召开,峰会以“RISC-V生态共建”为主题,结合当下全球新形势,把握全球新时机,呈现RISC-V全球新观点、新趋势。本次大会邀请了RISC-V国际基金会、业界专家、企业代表及社区伙伴等共同探讨RISC-V发展趋势与机遇,吸引超过百余家业界企业、高…...

软件设计师知识点·1
控制器: (1)指令寄存器(IR) : CPU执行一条指令时,从内存储器取到缓冲寄存器中,再送入IR暂存; (2)程序计数器(PC): 将要执行的下一条指令的地址; (3)地址寄存器(IR): 当前CPU所访问的内存单元地址; (4)指令译码器(ID): 对指令中的操作码字段进行分析解释; 多核CPU可以满足用户…...
修改Jupyter Notebook默认打开路径
这里我是重新下载的anaconda,打开Jupyter之后是默认在C盘的一个路径的,现在我们就来修改一下它的一个默认打开路径,这样在我们后续学习过程中,可以将ipynb后缀的文件放在这个目录下就能查看了。 1、先打开Anaconda Prompt&#x…...
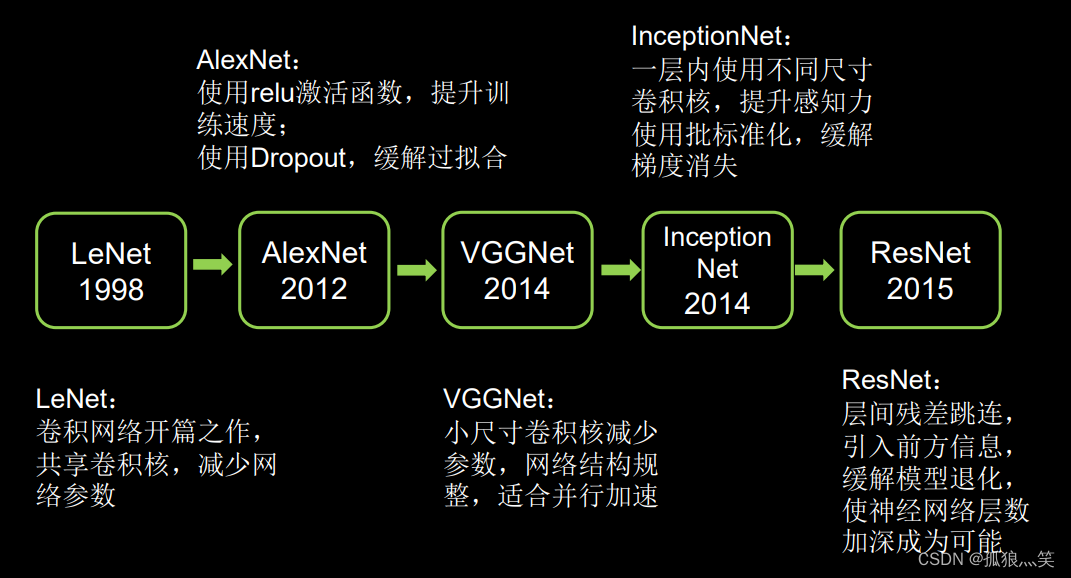
经典卷积网络
目录 一、经典神经网络出现的时间线编辑 二、LeNet 三、AlexNet 四、VGGNet 五、InceptionNet 六、ResNet 总结: 一、经典神经网络出现的时间线 二、LeNet 背景:LeNet由Yann LeCun于1998年提出,卷积网络开篇之作。 解释࿱…...

react+koa+vite前后端模拟jwt鉴权过程
路由组件(生成token) const Router require(koa/router) const jwt require(jsonwebtoken); const router new Router()const mockDbUserInfo [{nickname: xxxliu,username: Tom,password: 123456,icon: url1},{nickname: xxx,username: John,passw…...
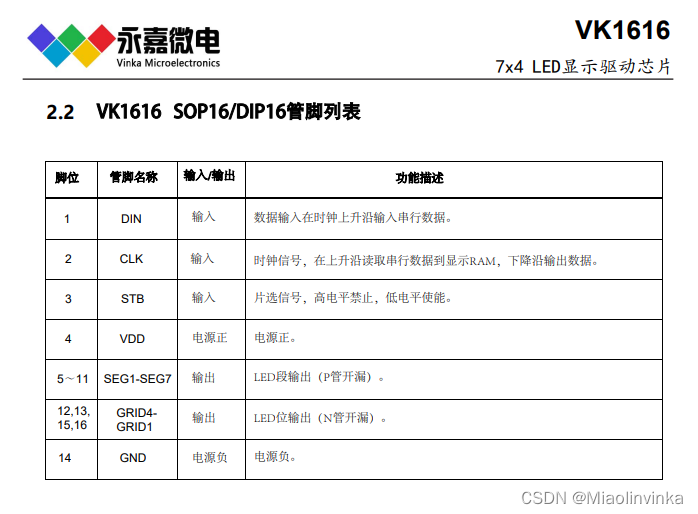
VK1616是LED显示控制驱动电路/LED驱动IC、数显驱动芯片、数码管驱动芯片
产品品牌:永嘉微电/VINKA 产品型号:VK1616 封装形式:SOP16 产品年份:新年份 概述:VK1616是一种数码管或点阵LED驱动控制专用芯片,内部集成有3线串行接口、数据锁存器、LED 驱动等电路。SEG脚接LED阳极&a…...
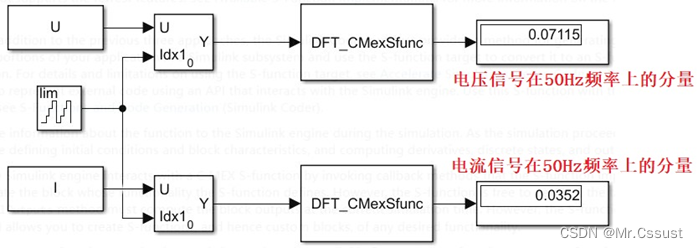
开箱报告,Simulink Toolbox库模块使用指南(五)——S-Fuction模块(C MEX S-Function)
文章目录 前言 C MEX S-Function 算法原理 原始信号创建 编写S函数 仿真验证 Tips 分析和应用 总结 前言 见《开箱报告,Simulink Toolbox库模块使用指南(一)——powergui模块》 见《开箱报告,Simulink Toolbox库模块使用…...
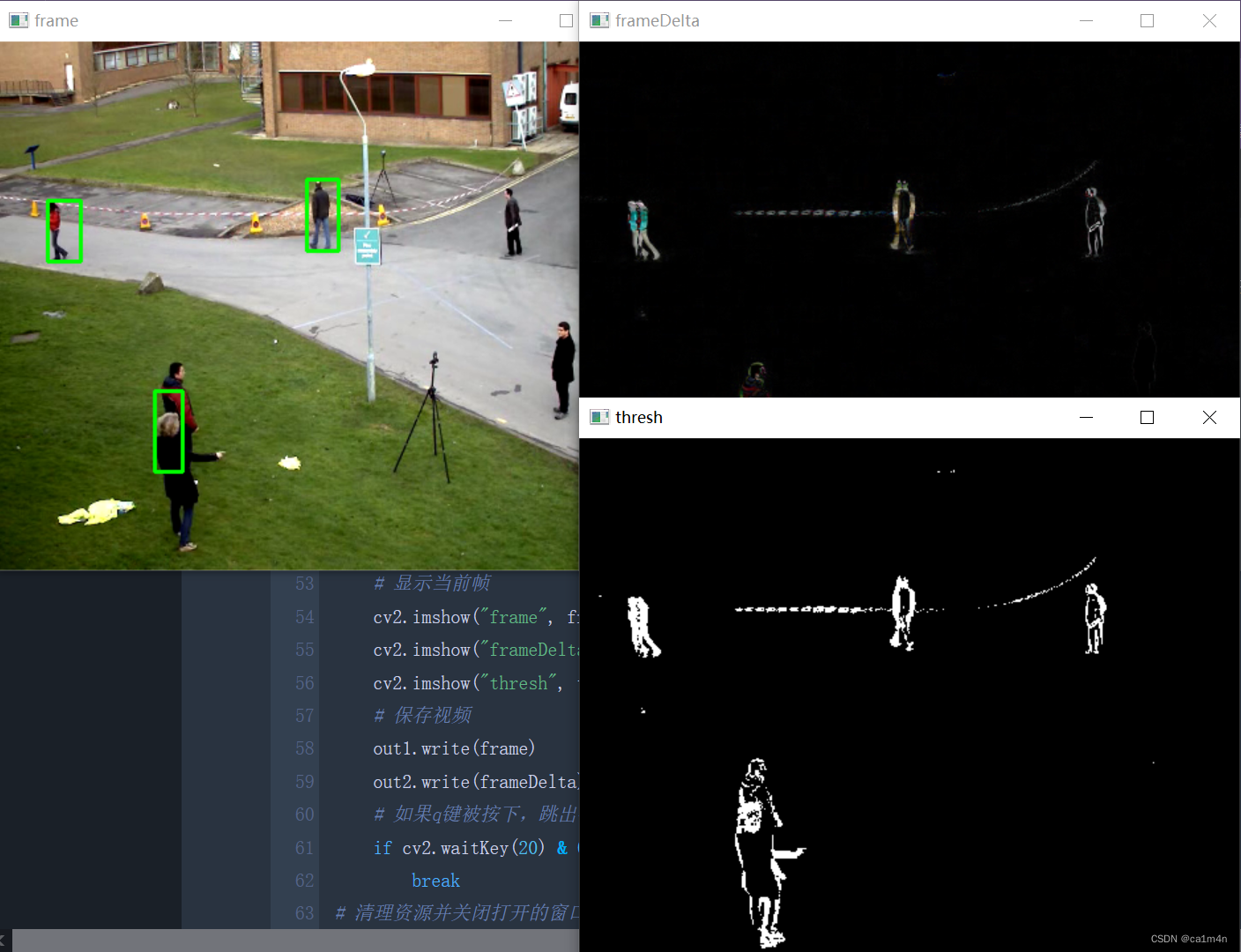
摄像头的调用和视频识别
CV_tutorial3 摄像头调用实时播放保存视频 运动目标识别帧差法背景减除法 摄像头调用 创建视频捕捉对象:cv2.VideoCapture() 参数为视频设备的索引号,就一个摄像投的话写0默认; 或者是指定要读取视频的路径。 实时播放 import cv2 import …...

多通道分离与合并
目录 1.多通道分离split() 2.多通道合并merge() 3.Android JNI demo 1.多通道分离split() void cv::split ( InputArray m, OutputArrayOfArrays mv ) m:待分离的多通道图像。 mv:分离后的单通道图像,为向量vector形式。 2.多通道合并merge…...

JOJO的奇妙冒险
JOJO,我不想再做人了。 推荐一部动漫 JOJO的奇妙冒险 荒木飞吕彦创作的漫画 《JOJO的奇妙冒险》是由日本漫画家荒木飞吕彦所著漫画。漫画于1987年至2004年在集英社的少年漫画杂志少年JUMP上连载(1987年12号刊-2004年47号刊),2005年后在集英…...
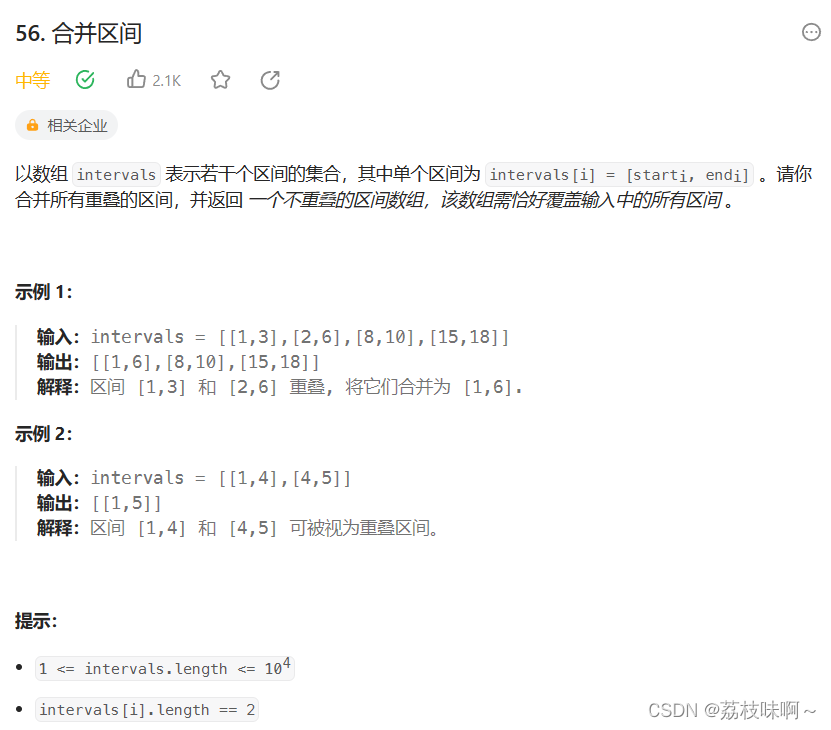
LeetCode56.合并区间
这道题我想了一会儿,实在想不到比较好的算法,只能硬着头皮写了,然后不断的debug,经过我不懈的努力,最后还是AC,不过效率确实低。 我就是按照最直接的方法来,先把intervals数组按照第一个数star…...

【内推码:NTAMW6c】 MAXIEYE智驾科技2024校招启动啦
MAXIEYE智驾科技2024校招启动啦【内推码:NTAMW6c】 【招聘岗位超多!!公司食堂好吃!!】 算法类:感知算法工程师、SLAM算法工程师、规划控制算法工程师、目标及控制算法工程师、后处理算法工程师 软件类&a…...
Python框架【模板继承 、继承模板实战、类视图 、类视图的好处 、类视图使用场景、基于调度方法的类视图】(四)
👏作者简介:大家好,我是爱敲代码的小王,CSDN博客博主,Python小白 📕系列专栏:python入门到实战、Python爬虫开发、Python办公自动化、Python数据分析、Python前后端开发 📧如果文章知识点有错误…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
