递归算法学习——子集

 

目录

一，题目解析

二，例子

三，题目接口

 四，解题思路以及代码

1.完全深度搜索

2.广度搜索加上深度优先搜索

五，相似题

1.题目

2.题目接口

 3.解题代码

---

一，题目解析

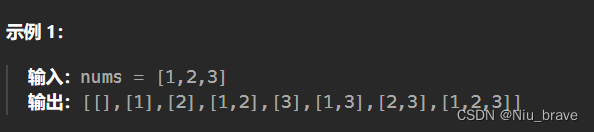
给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

二，例子

如以上例子，其实这道题里的子集的概念其实就是我们在高中时学习到的子集。一个含有n个数字的集合一共就有2^n个子集。空集是任何集合的子集。

三，题目接口

class Solution {
public:vector<vector<int>> subsets(vector<int>& nums) {}
};

 四，解题思路以及代码

1.完全深度搜索

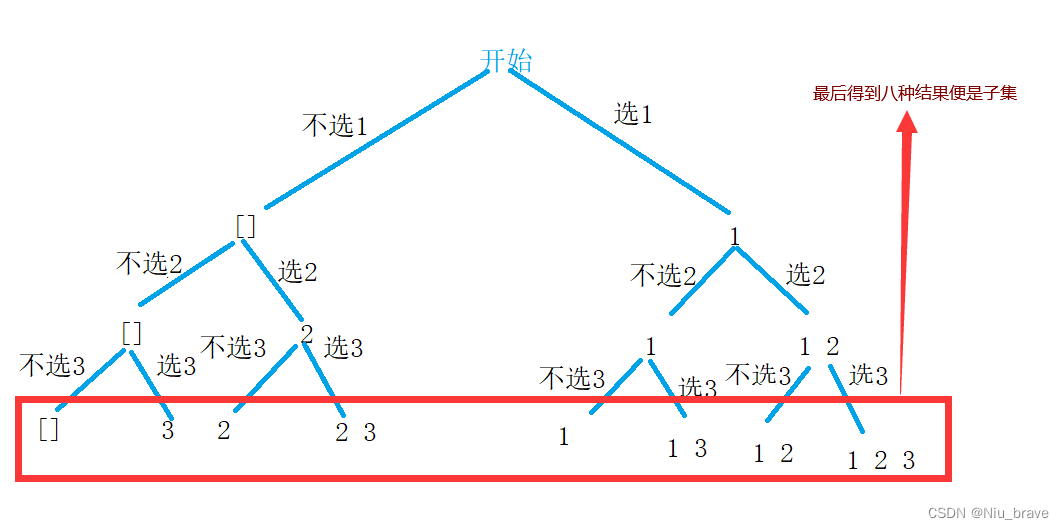
首先，我们可以来模拟一下这个集合完全通过深度优先搜索算法挑选子集的过程。先来说一说步骤，以数组{1，2，3}为例：

1.首先，我们得来做选择，在遍历到1时有两种选择，选和不选。通过这两种选择会导致两种不同的结果，也就是两种不同的集合。

2.到了第二层，遍历到了2这个数字。也会有两种不同的选择，又在上面一层的基础之上又会有四种不同的结果。

3.在最后一层遍历到3时，3的选与不选在上面两层的基础之上又会生成八种不同的结果。这8种结果便是我们要的所有子集。

画成图像如下：

按照这个思路写出的代码如下：

class Solution {
public:vector<int> path;vector<vector<int>>ret;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){if(pos == nums.size()){ret.push_back(path);return;}//在这一层选空节点dfs(nums,pos+1);//选对应的数字path.push_back(nums[pos]);dfs(nums,pos+1);path.pop_back();//递归完一层以后要还原现场，也就是回溯}
};

2.广度搜索加上深度优先搜索

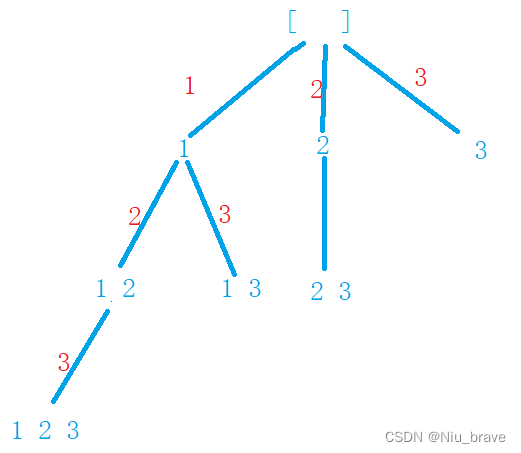
其实完全走深度优先搜索的方法其实效率不是很高，所以为了提高效率便可以将广度优先搜索算法给加入进来。以[1,2,3]为例，用这个算法的步骤如下：

1.首先，一言不合便开始将path加入到ret中，那在第一次假如时便将空集给加入到ret中了。

2.将这一层中的元素加入到path中，然后再往下递归。

3.再次插入元素到path，再插入到ret中。再往下递归。递归结束的时候下标的值是等于数组的元素个数的。在递归完了以后也要回溯恢复现场。

图解过程如下：

代码如下：

class Solution {
public:vector<int> path;vector<vector<int>>ret;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}void dfs(vector<int>& nums,int pos){ret.push_back(path);//一言不合便将path塞入到ret中for(int i = pos;i<nums.size();i++)//其实这里边相当于一个递归的结束条件{path.push_back(nums[i]);dfs(nums,i+1);//递归下一层path.pop_back();//回溯，恢复现场}  }
};

五，相似题

1.题目

一个数组的 异或总和 定义为数组中所有元素按位 XOR 的结果；如果数组为 空 ，则异或总和为 0 。

• 例如，数组 [2,5,6] 的 异或总和 为 2 XOR 5 XOR 6 = 1 。

给你一个数组 nums ，请你求出 nums 中每个 子集 的 异或总和 ，计算并返回这些值相加之 和 。

注意：在本题中，元素 相同 的不同子集应 多次 计数。

数组 a 是数组 b 的一个 子集 的前提条件是：从 b 删除几个（也可能不删除）元素能够得到 a 。

2.题目接口

class Solution {
public:int subsetXORSum(vector<int>& nums) {}
};

 3.解题代码

其实这道题和子集这道题的代码可太像了，所以不多赘述，代码如下：

class Solution {
public:int sum;int path;int subsetXORSum(vector<int>& nums) {dfs(nums,0);return sum;}void dfs(vector<int>&nums,int pos){sum+=path;for(int i = pos;i<nums.size();i++){path = path^nums[i];dfs(nums,i+1);path = path^nums[i];//消消乐定律，这一层的自己和自己异或便是恢复上一层样子。}}
};