(笔记五)利用opencv进行图像几何转换
参考网站:https://docs.opencv.org/4.1.1/da/d6e/tutorial_py_geometric_transformations.html
(1)读取原始图像和标记图像
import cv2 as cv
import numpy as np
from matplotlib import pyplot as pltpath = r"D:\data\flower.jpg"
img = cv.imread(path)
img = cv.cvtColor(img, cv.COLOR_BGR2RGB)# 拷贝图像
img1 = np.copy(img)
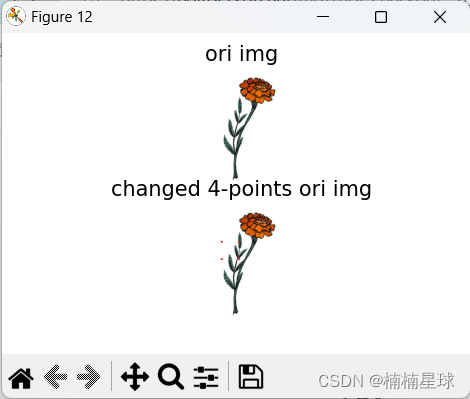
img1[100:105, 100:105, :] = [255, 0, 0] # main point is (103, 103)
img1[100:105, 150:155, :] = [255, 0, 0] # main point is (103, 153)
img1[150:155, 100:105, :] = [255, 0, 0] # main point is (153, 103)
img1[150:155, 150:155, :] = [255, 0, 0] # main point is (153, 153)
plt.figure(12)
plt.subplot(211), plt.imshow(img), plt.title('ori img'), plt.axis('off')
plt.subplot(212), plt.imshow(img1), plt.title('changed 4-points ori img'), plt.axis('off')
# plt.show()
(2)改变图像分辨率
# 改变分辨率
img2 = np.copy(img)
# dsize = None,fx是x相对于原来的x要改变的比例,同理y
img3 = cv.resize(img2, None, fx=0.1, fy=0.1, interpolation=cv.INTER_CUBIC)
img4 = cv.resize(img2, None, fx=10, fy=10, interpolation=cv.INTER_CUBIC)
plt.figure(3)
plt.subplot(311), plt.imshow(img), plt.title('ori img resolution:' + str(img.shape[0:2])), plt.axis('off')
plt.subplot(312), plt.imshow(img3), plt.title('0.1 times resolution:' + str(img3.shape[0:2])), plt.axis('off')
plt.subplot(313), plt.imshow(img4), plt.title('10 times resolution:' + str(img4.shape[0:2])), plt.axis('off')
# plt.show()

(3)平移图像
核心函数:cv.warpAffine(img, M, (col, row))
# 图像平移
img5 = np.copy(img)
row, col, sp = img5.shape
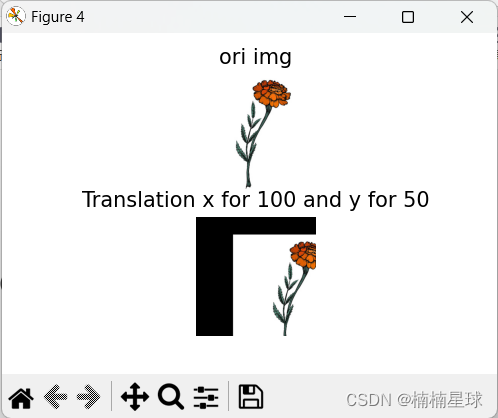
M1 = np.float32([[1, 0, 100], [0, 1, 50]]) # x平移100,y平移50
print('图像平移:')
print('图像平移所计算的转换矩阵为:', M1)
img6 = cv.warpAffine(img5, M1, (col, row)) # warpAffine函数利用转移矩阵平移
plt.figure(4)
plt.subplot(211), plt.imshow(img), plt.title('ori img'), plt.axis('off')
plt.subplot(212), plt.imshow(img6), plt.title('Translation x for 100 and y for 50'), plt.axis('off')
# plt.show()

(4)图像旋转
核心函数:M=cv.getRotationMatrix2D(((旋转中心坐标(x,y)), 旋转角度, 相向尺度因子)
cv.warpAffine(img, M, (col, row))

# 图像旋转
img7 = np.copy(img)
# 图像中心,图像旋转角度,图像同向比例因子
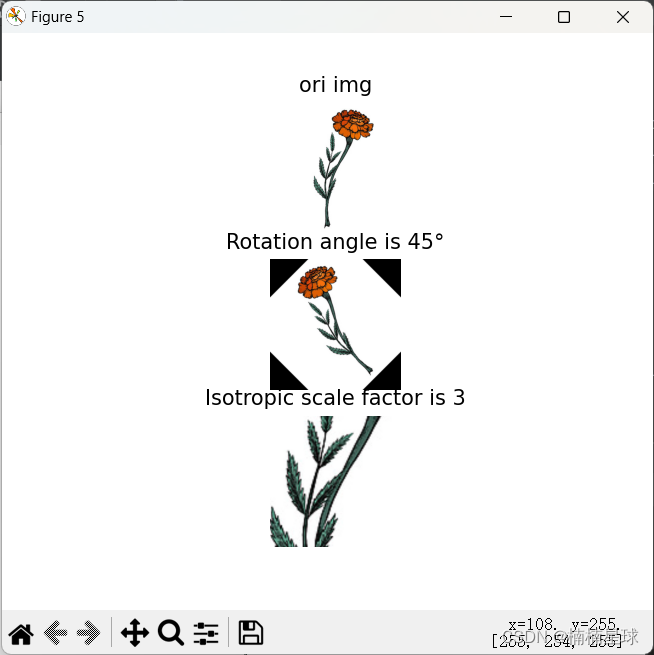
M2 = cv.getRotationMatrix2D(((col - 1) / 2, (row - 1) / 2), 45, 1)
M3 = cv.getRotationMatrix2D(((col - 1) / 2, (row - 1) / 2), 0, 3)
print('图像旋转:')
print('旋转一的转换矩阵:', M2)
print('旋转二的转换矩阵:', M3)
img8 = cv.warpAffine(img7, M2, (col, row))
img9 = cv.warpAffine(img7, M3, (col, row))
plt.figure(5)
plt.subplot(311), plt.imshow(img), plt.title('ori img'), plt.axis('off')
plt.subplot(312), plt.imshow(img8), plt.title('Rotation angle is 45°'), plt.axis('off')
plt.subplot(313), plt.imshow(img9), plt.title('Isotropic scale factor is 3'), plt.axis('off')
# plt.show()

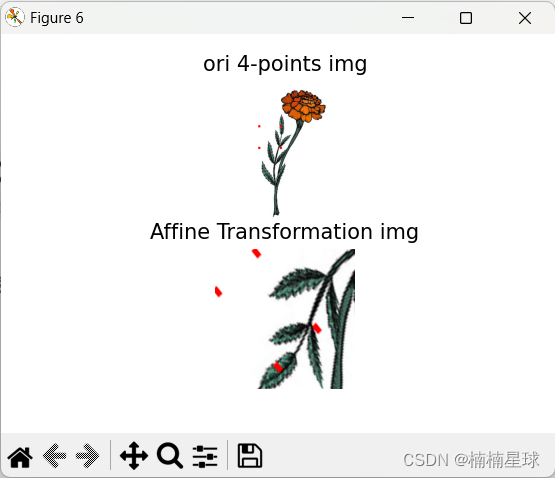
(5)图像仿射变换
核心函数:M=cv.getAffineTransform(原图三个点坐标, 转换图三个点坐标)
cv.warpAffine(img, M, (col, row))

# 仿射变换
img10 = np.copy(img1)
points_one = np.float32([[103, 103], [103, 153], [153, 103]]) # 原始图像三个点坐标
points_two = np.float32([[10, 100], [100, 10], [150, 275]]) # 仿射变换目标图像的三个点坐标
M4 = cv.getAffineTransform(points_one, points_two)
print('仿射变换:')
print('仿射变换的转换矩阵:', M4)
img11 = cv.warpAffine(img10, M4, (col, row))
plt.figure(6)
plt.subplot(211), plt.imshow(img1), plt.title('ori 4-points img'), plt.axis('off')
plt.subplot(212), plt.imshow(img11), plt.title('Affine Transformation img'), plt.axis('off')
# plt.show()
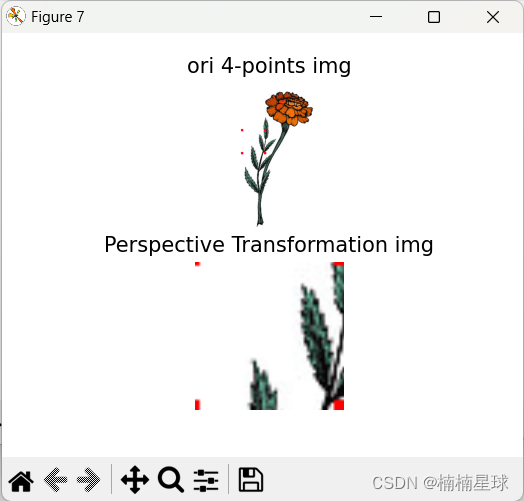
(6)图像透射变换
核心函数:M=cv.getPerspectiveTransform(原图四个点坐标,转换图像四个点坐标 )
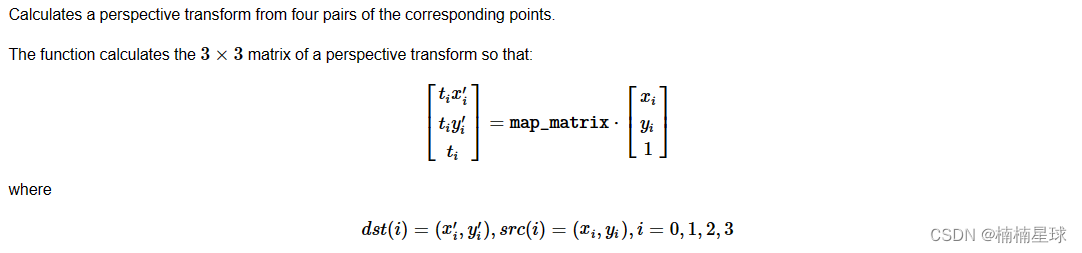
cv.warpPerspective(img, M, (转换图长宽))
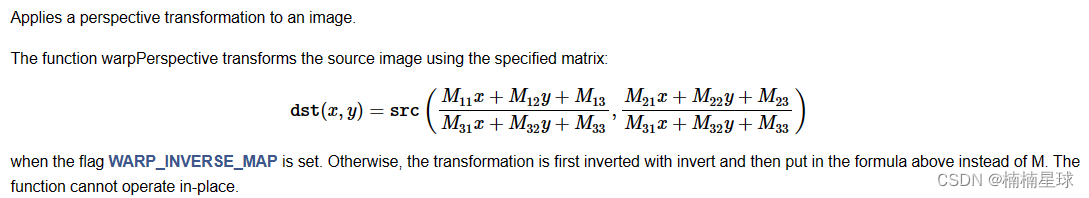
# 透射变换
img12 = np.copy(img1)
points_one_one = np.float32([[103, 103], [103, 153], [153, 103], [153, 153]]) # 原始图像四个点坐标
points_two_two = np.float32([[0, 0], [0, 300], [300, 0], [300, 300]]) # 透射变换目标图像的四个点坐标
M5 = cv.getPerspectiveTransform(points_one_one, points_two_two)
print('透射变换:')
print('透射变换的转换矩阵:', M5)
# img12为要转换的图像,M5为透射变换的转换矩阵,dsize为目标图像大小
img13 = cv.warpPerspective(img12, M5, (300, 300))
plt.figure(7)
plt.subplot(211), plt.imshow(img1), plt.title('ori 4-points img'), plt.axis('off')
plt.subplot(212), plt.imshow(img13), plt.title('Perspective Transformation img'), plt.axis('off')
plt.show()

相关文章:

(笔记五)利用opencv进行图像几何转换
参考网站:https://docs.opencv.org/4.1.1/da/d6e/tutorial_py_geometric_transformations.html (1)读取原始图像和标记图像 import cv2 as cv import numpy as np from matplotlib import pyplot as pltpath r"D:\data\flower.jpg&qu…...
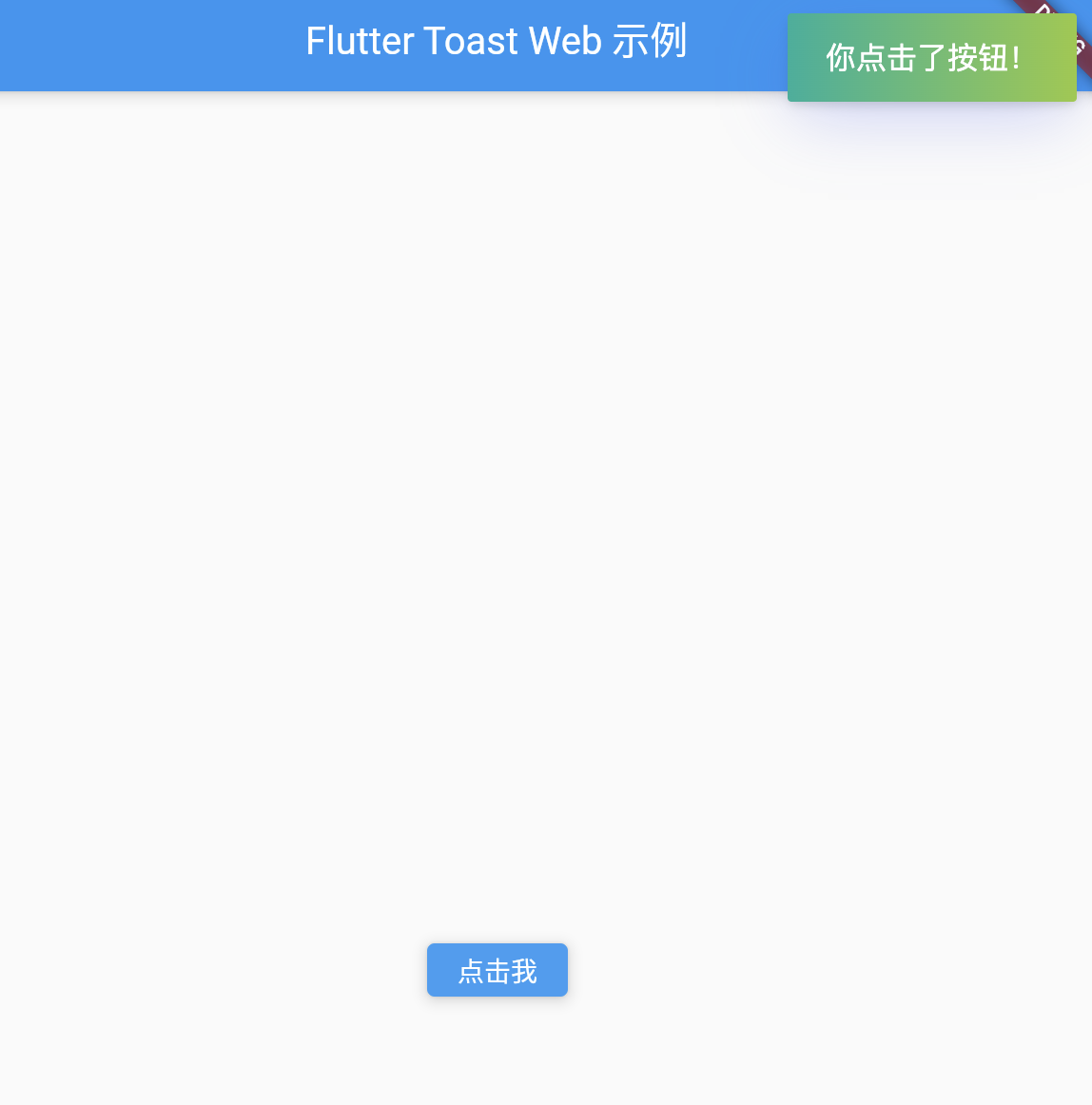
【Flutter】Flutter 使用 fluttertoast 实现显示 Toast 消息
【Flutter】Flutter 使用 fluttertoast 实现显示 Toast 消息 文章目录 一、前言二、安装和基础使用三、不同平台的支持情况四、如何自定义 Toast五、在实际业务中的应用六、完整的业务代码示例(基于 Web 端)七、总结 一、前言 在这篇文章中,…...
nowcoder NC236题 最大差值
目录 题目描述: 示例1 示例2 题干解析: 暴力求解: 代码展示: 优化: 代码展示: 题目跳转https://www.nowcoder.com/practice/a01abbdc52ba4d5f8777fb5dae91b204?tpId128&tqId33768&ru/exa…...
TCP/IP五层模型、封装和分用
1.网络通信基础2.协议分层OSI七层协议模型TCP/IP五层/四层协议模型【重点】 3. 封装&分用 1.网络通信基础 IP地址:表示计算机的位置,分源IP和目标IP;举个例子:买快递,商家从上海发货,上海就是源IP&…...

LeetCode 面试题 01.08. 零矩阵
文章目录 一、题目二、C# 题解 一、题目 编写一种算法,若M N矩阵中某个元素为0,则将其所在的行与列清零。 点击此处跳转题目。 示例 1: 输入: [ [1,1,1], [1,0,1], [1,1,1] ] 输出: [ [1,0,1], [0,0,0], [1,0,1] ] 示…...

Qt应用开发(基础篇)——进度条 QProgressBar
一、前言 QProgressBar类继承于QWidget,是一个提供了横向或者纵向进度条的小部件。 QProgressBar进度条一般用来显示用户某操作的进度,比如烧录、导入、导出、下发、上传、加载等这些需要耗时和分包的概念,让用户知道程序还在正常的执行中。 …...
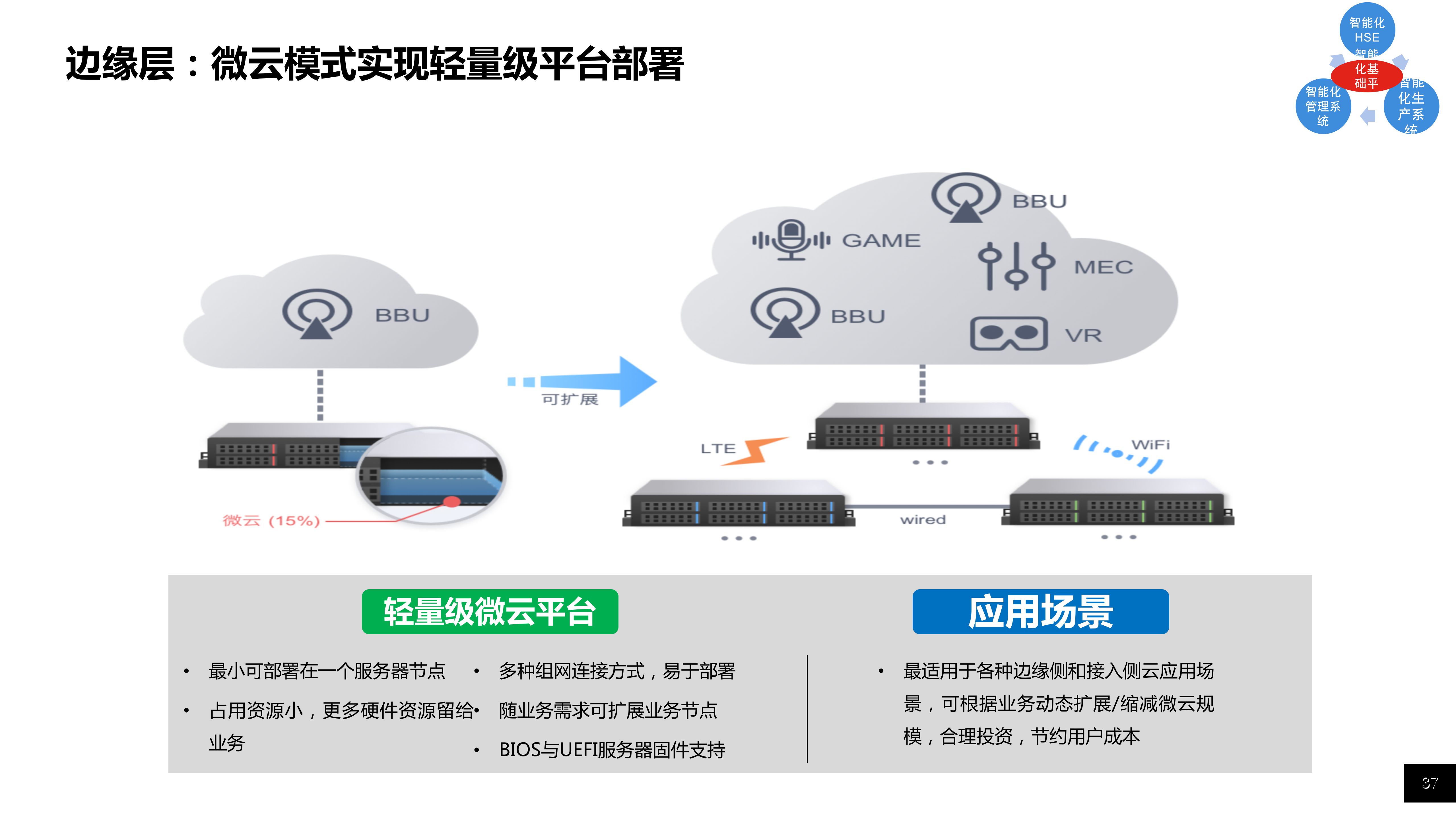
108页石油石化5G智慧炼化厂整体方案PPT
导读:原文《108页石油石化5G智慧炼化厂整体方案PPT》(获取来源见文尾),本文精选其中精华及架构部分,逻辑清晰、内容完整,为快速形成售前方案提供参考。以下是部分内容,...

Codeforces 1625E2 括号树 + BIT
题意 传送门 Codeforces 1625E2 Cats on the Upgrade (hard version) 题解 首先利用栈将原始字符串转换为合法的 RBS,不能匹配的括号设为 ‘.’。根据匹配的括号序列构造树,具体而言,遇到左括号,则新建节点向下递归,…...

PHP命令行CLI的使用
PHP命令行界面 PHP命令行界面(CLI)是一种使用命令行(终端)来运行PHP脚本的方式,与在Web服务器环境下运行PHP不同。CLI提供了一种与操作系统交互的方式,能够在命令行中直接执行PHP代码。 以下是一些与PHP命…...

近期嵌软线下笔试题记录
1、以下代码的输出结果是? #include <stdio.h> #include <string.h>int main() {int a,b,c,d;a 10;b a; //a先赋值给b,然后自增1c a; //a自增1后赋值给cd 10*a; //先进行运算然后a自增1printf("b,c,d:%d…...
基于MYSQL的主从同步和读写分离
目录 一.完成MySQL主从同步(一主两从) 1.主库配置 2.建立同步账号 3.锁表设置只读 4.备份数据库数据 5.主库备份数据上传到从库 6.从库上还原备份 7.解锁 8.从库上设定主从同步 9.启动从库同步开关 10.检查状态 二.基于MySQL一主两从配置&…...

java八股文面试[多线程]——合适的线程数是多少
知识来源: 【并发与线程】 合适的线程数量是多少?CPU 核心数和线程数的关系?_哔哩哔哩_bilibili 【2023年面试】程序开多少线程合适_哔哩哔哩_bilibili...

Linux系统下vim常用命令
一、基础命令: v:可视模式 i:插入模式 esc:命令模式下 :q :退出 :wq :保存并退出 ZZ:保存并退出 :q! :不保存并强制退出二、在Esc下: dd : 删除当前行 yy:复制当前行 p:复制已粘贴的文本 u:撤销上一步 U:…...

【2023】LeetCode HOT 100——链表
目录 1. 相交链表1.1 C++实现1.2 Python实现1.3 时空分析2. 反转链表2.1 C++实现2.2 Python实现2.3 时空分析3. 回文链表3.1 C++实现3.2 Python实现3.3 时空分析4. 环形链表4.1 C++实现4.2 Python实现4.3 时空分析5. 环形链表 II5.1 C++实现5.2 Python实现...
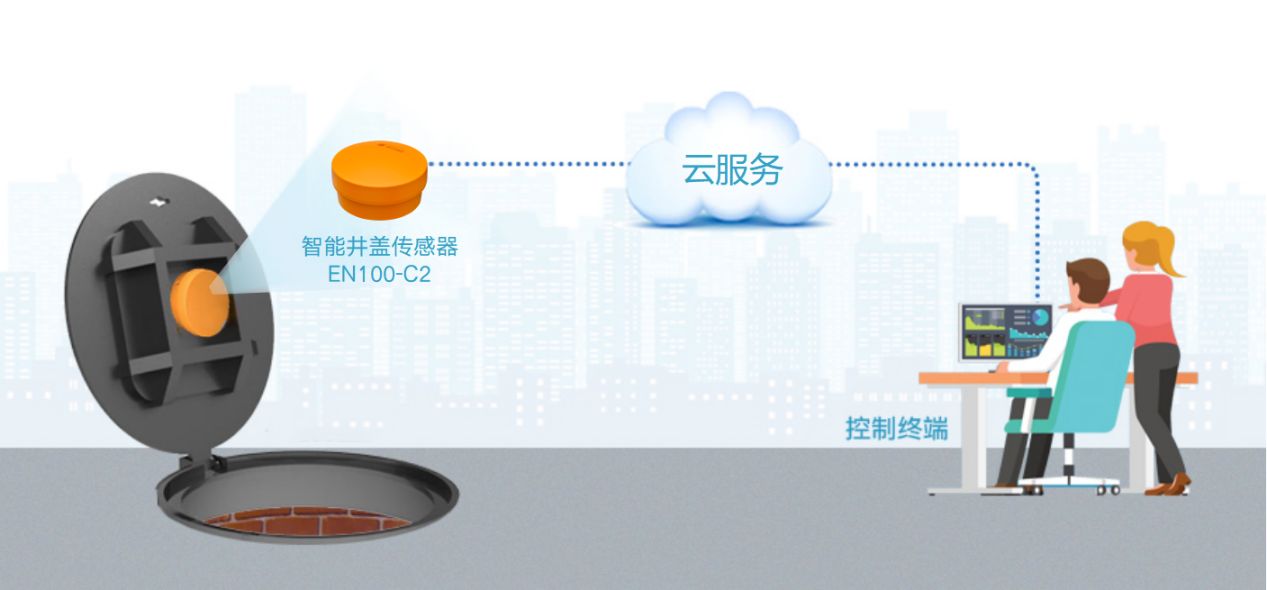
智能井盖传感器,物联网智能井盖系统
随着城市人口的不断增加和城市化进程的不断推进,城市基础设施的安全和可靠性变得愈发重要,城市窨井盖作为城市基础设施重要组成部分之一,其安全性事关城市安全有序运行和居民生产生活安全保障。 近年来,各地都在加强城市窨井盖治理…...

C语言三子棋解析
目录(标2的是我自己写的一堆问题不知道怎么改) 开始菜单1打印棋盘1玩家下棋1电脑下棋1判断输赢1开始菜单2打印棋盘2选择先后2玩家下棋2电脑下棋2判断输赢2完整代码文件else.h文件else.c文件test.c 开始菜单1 void menu()//打印菜单 {printf("*****…...
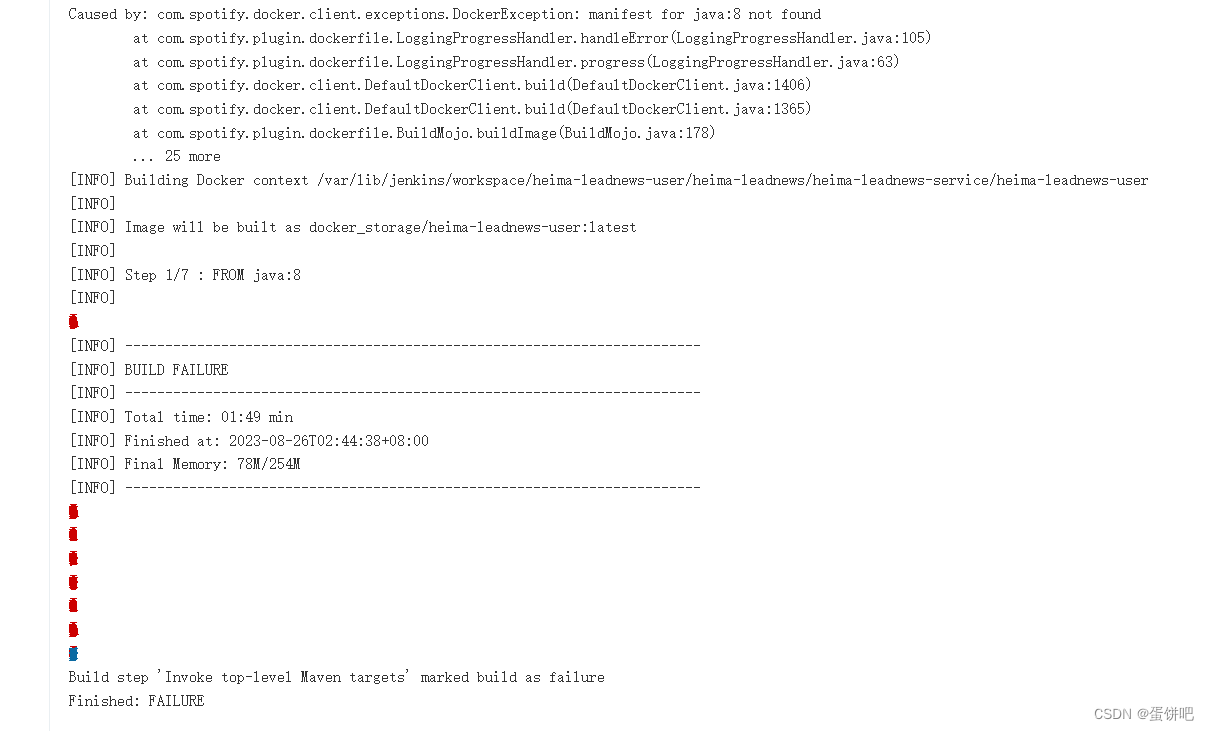
【Jenkins打包服务,Dockerfile报错:manifest for java : 8 not fourd】
1、问题描述 Jenkins打包服务运行dockerfile里的FROM java:8报错manifest for java : 8 not fourd Caused by: com.spotify. docker.client.exceptions.DockerException: manifest for java:8 not found2、解决方法 在网上查找许多方法后得出这是由于Docker官方已经弃用java…...
读SQL学习指南(第3版)笔记06_连接和集合
1. 连接 1.1. 笛卡儿积 1.1.1. 交叉连接(cross join) 1.1.2. 查询并没有指定两个数据表应该如何连接,数据库服务器就生成了笛卡儿积 1.1.2.1. 两个数据表的所有排列组合 1.1.3. 很少会用到(至少不会特意用到) 1.…...

C#学习,结构,面向对象,类
结构和类 结构是从过程化程序设计中保留下来的一种数据类型,类则是面向对象程序设计中最基本的、也是最重要的概念。 结构 结构是一种值类型,通常用来封装一组相关的变量,结构中可以包含构造函数、变量、字段、方法、属性、运算符、事件和…...

【PHP】文件操作
文章目录 文件编程的必要性目录操作其它目录操作递归遍历目录PHP5常见文件操作函数PHP4常见文件操作函数其他文件操作函数 文件编程的必要性 文件编程指利用PHP代码针对文件(文件夹)进行增删改查操作。 在实际开发项目中,会有很多内容&…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
