LeetCode 双周赛 98,脑筋急转弯转不过来!
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。
大家好,我是小彭。
昨晚是 LeetCode 第 98 场双周赛,你参加了吗?这场周赛需要脑筋急转弯,转不过来 Medium 就会变成 Hard,转得过来就变成 Easy。


2566. 替换一个数字后的最大差值(Easy)
题目地址
https://leetcode.cn/problems/maximum-difference-by-remapping-a-digit/
题目描述
给你一个整数 num 。你知道 Danny Mittal 会偷偷将 0 到 9 中的一个数字 替换 成另一个数字。
请你返回将 num 中 恰好一个 数字进行替换后,得到的最大值和最小值的差位多少。
注意:
- 当 Danny 将一个数字
d1替换成另一个数字d2时,Danny 需要将nums中所有d1都替换成d2。 - Danny 可以将一个数字替换成它自己,也就是说
num可以不变。 - Danny 可以将数字分别替换成两个不同的数字分别得到最大值和最小值。
- 替换后得到的数字可以包含前导 0 。
- Danny Mittal 获得周赛 326 前 10 名,让我们恭喜他。
题解(字符串操作)
- 技巧:将整型转换为字符串能够更方便地修改具体位置。
简单模拟题,有 2 个思路:
- 思路 1 - 暴力枚举:尝试枚举每类的数字,将其替换为
9取得最大值,将其替换为0取得最小值,最后取所有方案的最大值和最小值取差值; - 思路 2 - 贪心思路:替换越靠近 “高位” 的数字能够使得差值越大,所以我们将从高位开始的首个非
9数字替换为9(例如90替换为99)必然得到最大值,将从高位开始的首个数字替换为0(例如90替换为00)必然得到最小值。
// 思路 1
class Solution {fun minMaxDifference(num: Int): Int {val numStr = "$num"var max = numvar min = numfor (element in numStr) {max = Math.max(max, numStr.replace(element, '9').toInt())min = Math.min(min, numStr.replace(element, '0').toInt())}return max - min}
}
复杂度分析:
- 时间复杂度:O(log2num)O(log^2\,{num})O(log2num) 数字最多有 log num 位,外层循环与内存循环的字符串替换操作都是 O(lognum)O(log\,{num})O(lognum) 时间级别复杂度;
- 空间复杂度:O(lognum)O(log\,{num})O(lognum) 字符串占用空间。
// 思路 2
class Solution {fun minMaxDifference(num: Int): Int {val numStr = "$num"val min = numStr.replace(numStr[0], '0').toInt()var max = numfor (element in numStr) {if ('9' != element) {max = numStr.replace(element, '9').toInt()break}}return max - min}
}
复杂度分析:
- 时间复杂度:O(lognum)O(log\,{num})O(lognum) 内存循环的字符串替换操作最多只会执行一次,均摊下来整体只有 O(lognum)O(log\,{num})O(lognum) 级别的时间复杂度;
- 空间复杂度:O(lognum)O(log\,{num})O(lognum) 字符串占用空间。
2567. 修改两个元素的最小分数(Medium)
题目地址
https://leetcode.cn/problems/minimum-score-by-changing-two-elements/
题目描述
给你一个下标从 0 开始的整数数组 nums 。
nums的 最小 得分是满足0 <= i < j < nums.length的|nums[i] - nums[j]|的最小值。nums的 最大 得分是满足0 <= i < j < nums.length的|nums[i] - nums[j]|的最大值。nums的分数是 最大 得分与 最小 得分的和。
我们的目标是最小化 nums 的分数。你 最多 可以修改 nums 中 2 个元素的值。
请你返回修改 nums 中 至多两个 元素的值后,可以得到的 最小分数 。
|x| 表示 x 的绝对值。
题解(排序 + 枚举)
这道题也有脑筋急转弯的成分,同时我们可以扩展思考下 “最多修改 k 个元素的最小得分” 问题,最后再说。
这道题的关键在于得分的定义:
- “最小得分” 表示任意数组中两个数字之间的最小绝对差;
- “最大得分” 表示任意数组中两个数字之间的最大绝对差。
理解题意后容易发现:
- 影响 “最小得分” 的是数组中最接近的两个数字。当数组中存在两个相同元素时,“最小得分” 可以取到最小值 0;
- 影响 “最大得分” 的是数组中最不接近的两个数,即最大值和最小值。当我们将最大值和最小值修改为数组中间的某个元素时,能使得差值变小的同时,保持 “最小得分” 取最小值 0。
因此得知: 这道题的关键点在于修改数组的最大值或最小值成为数组中间的某个元素。 要么让最大值变小,要么让最小值变大。由于题目最多只能修改 2 次,因此最多只能以下 3 种情况:
- 情况 1:修改数组中最大的两个数为
nums[n - 3]; - 情况 2:修改数组中最小的两个数为
nums[2]; - 情况 3:修改数组的最大值为
nums[n - 1],修改数组的最小值为nums[1]。
简单枚举出 3 种情况的解后再进行一轮比较即可。
最后再观察边界条件,数组的最小长度为 3,所以不需要特判。
class Solution {fun minimizeSum(nums: IntArray): Int {nums.sort()val n = nums.sizeval choice1 = nums[n - 3] - nums[0]val choice2 = nums[n - 1] - nums[2]val choice3 = nums[n - 2] - nums[1]return Math.min(choice1, Math.min(choice2, choice3))}
}
复杂度分析:
- 时间复杂度:O(nlgn)O(nlgn)O(nlgn) 快速排序占用的时间,如果手动维护最小的 3 个元素和最大的 3 个元素可以降低到 O(n)O(n)O(n) 时间复杂度;
- 空间复杂度:O(lgn)O(lgn)O(lgn) 排序占用的递归栈空间。
再扩展思考一下,如果题目说明最多可以修改 k(0≤k≤nums.length)k (0 ≤ k ≤ nums.length)k(0≤k≤nums.length)次的话,应该解决问题呢? —— 即 “求最多修改 k 个元素的最小得分”,原题就是 k = 2 的情况。
那么这道题就是考察 “滑动窗口” 技巧了,我们可以将修改的范围视为一个跨越数组首尾且长度为 k 的滑动窗口,那么而问题的答案就取决于 “不被” 滑动窗口包围的另一部分。再逆向思考一下,我们可以用长度为 length - k 的滑动窗口在数组上移动,并记录窗口首尾元素的差值,枚举所有情况后记录最小值即为最小得分:
举个例子,在输入数组为 [1, 4, 5, 7, 8] ,k = 2 时,前文提到的 3 种方案分别对应以下 3 个窗口状态:
- 情况 1:修改数组中最大的两个数:
1,4 | 5,7,8 | - 情况 2:修改数组中最小的两个数:
| 1,4,5 | 7,8 - 情况 3:修改数组的最大值和最小值:
1 | 4,5,7 | 8
class Solution {fun minimizeSum(nums: IntArray): Int {val n = nums.size// 操作次数val k = 2// 滑动窗口val len = n - knums.sort()var min = Integer.MAX_VALUEfor (left in 0..n - len) {val right = left + len - 1min = Math.min(min, nums[right] - nums[left])}return min}
}
复杂度分析同上。
2568. 最小无法得到的或值(Medium)
题目地址
https://leetcode.cn/problems/minimum-impossible-or/
题目描述
给你一个下标从 0 开始的整数数组 nums 。
如果存在一些整数满足 0 <= index1 < index2 < ... < indexk < nums.length ,得到 nums[index1] | nums[index2] | ... | nums[indexk] = x ,那么我们说 x 是 可表达的 。换言之,如果一个整数能由 nums 的某个子序列的或运算得到,那么它就是可表达的。
请你返回 nums 不可表达的 最小非零整数 。
题解一(散列表)
相似题目:2154. 将找到的值乘以 2
这道题需要脑筋急转弯。
首先,我们先观察输入数据范围中小数值的二进制表示,尝试发现规律:
- 0 = 0000 = 0
- 1 = 0001 = 1
- 2 = 0010 = 2
- 3 = 0011 = 2 | 1
- 4 = 0100 = 4
- 5 = 0101 = 4 | 1
- 6 = 0110 = 4 | 2
- 7 = 0111 = 4 | 2 | 1,或者 5 | 1
- 8 = 1000 = 8
- 9 = 1001 = 8 | 1
- 10 = 1010 = 8 | 2
我们发现以下 2 点信息:
- 除了数字 7 = 5 | 1 的特殊方案外,其他数字的表示方案都可以由形如 x=2i∣2j∣2kx = 2^i | 2^j | 2^ kx=2i∣2j∣2k 的格式表达(很容易理解);
- 2i2^i2i 格式的数字不可能被其他数用 “或” 的形式表示(也很容易理解)。
由此可以得出结论: 影响数组最小可表达数的关键在于数组中 “未出现的最小的 2i2^i2i”,并且这个数就是不可表达的最小非零数。
举例说明:假设 8 是数组中未出现的最小 2i2^i2i(此时 [1, 2, 4] 肯定在数组中出现2i2^i2i),那么数字 1 ~ 7 之间的所有数字都可以由 [1、2、4] 通过或表示,而 8 无法被 [1, 2, 3, 4, 5, 6 ,7] 之间的任何数字表达,同时也无法被大于 8 的其他数表示,因此 8 就是最小的可表达数。
完成问题转换后编码就很容易了,我们只要从小到大枚举所有 2i2^i2i ,并检查它是否在数组中出现即可:
class Solution {fun minImpossibleOR(nums: IntArray): Int {val numSet = nums.toHashSet()var i = 1while (numSet.contains(i)) {i = i shl 1}return i}
}
复杂度分析:
- 时间复杂度:O(n+logU)O(n + logU)O(n+logU) 其中 n 是数组长度,U 是数组的最大值,最多只需要检查 logU 位数字;
- 空间复杂度:O(n)O(n)O(n) 散列表占用的空间。
题解二(位运算)
题解一使用散列表来辅助判断 2i2^i2i 是否存在于数组中,可以进一步优化:我们将直接从数组元素的二进制数据中提取特征值,并还原出 “未出现的最小的 2i2^i2i”:
- 1、遍历数组中所有元素,如果元素值是 2i2^i2i 则将其记录到 mask 特征值中;
- 2、遍历结束后将得到形如
0011, 1011格式的特征值,此时 “未出现的最小的 2i2^i2i” 正好位于从低位到高位出现的首个 0 的位置,即0000, 0100; - 3、为了还原出目标数,执行以下位运算:
x = ~x // 按位取反: 0011,1011 => 1100,0100
x & -x // lowbit 公式:1100,0100 => 0000,0100
class Solution {fun minImpossibleOR(nums: IntArray): Int {var mask = 0for (x in nums) {// x & (x - 1) 将消除最低位的 1,如果消除后值为 1 说明 x 本身就是 2 的幂if (x and (x - 1) == 0) mask = mask or x}// 取反mask = mask.inv()// 取最低位 1 return mask and -mask}
}复杂度分析:
- 时间复杂度:O(n)O(n)O(n) 其中 n 是数组长度;
- 空间复杂度:O(1)O(1)O(1) 仅占用常数级别空间。
2569. 更新数组后处理求和查询(Hard)
题目地址
https://leetcode.cn/problems/handling-sum-queries-after-update/
题目描述
给你两个下标从 0 开始的数组 nums1 和 nums2 ,和一个二维数组 queries 表示一些操作。总共有 3 种类型的操作:
- 操作类型 1 为
queries[i] = [1, l, r]。你需要将nums1从下标l到下标r的所有0反转成1或将1反转成0。l和r下标都从 0 开始。 - 操作类型 2 为
queries[i] = [2, p, 0]。对于0 <= i < n中的所有下标,令nums2[i] = nums2[i] + nums1[i] * p。 - 操作类型 3 为
queries[i] = [3, 0, 0]。求nums2中所有元素的和。
请你返回一个数组,包含所有第三种操作类型的答案。
预备知识
类似的区间求和问题,我们先回顾一下解决方案:
- 1、静态数组求区间和:「前缀和数组」、「树状数组」、「线段树」
- 2、频繁单点更新,求区间和:「树状数组」、「线段树」
- 3、频繁区间更新,求具体位置:「差分数组」
- 4、频繁区间更新,求区间和:「线段树 + 懒更新」
这道题涉及 “区间更新” 和 “区间求和”,所以属于线段树的典型例题。
题解一(朴素线段树)
我们先理解题目中三种操作的含义:
- 操作一:对
nums1数组中位于[left, right]区间的数进行反转,也就是进行 “区间更新”; - 操作二:将
nums1数组上的数值nums1[index]乘以p后累加到nums2数组的相同位置上,即nums2[index] += nums1[index] * p,同样也是进行 “区间更新”; - 操作三:求
nums2数组中所有元素和,即 “求区间和”。
OK,既然操作一和操作二是对不同数组进行 “区间更新”,那么我们需要分别为这两个数组建立线段树吗?并不需要,这是题目抛出的烟雾弹。
因为题目最终的解是求 nums2 数组的全体和,所以我们并不需要真正地维护 nums2 数组,只需要将操作二的增量累加到全体和中。这样的话就是只需要维护 nums1 数组的线段树。
理解题意后,我们可以写出题解的主框架:
- 1、首先计算
nums2数组的初始全体和sum; - 2、建立
nums1数组的线段树; - 3、依次处理每种操作,操作一对线段树做区间更新,操作二对线段树做区间求和后乘以
p,并累加到全体和sum中,操作三将sum推入结果列表。
// 程序主框架
class Solution {fun handleQuery(nums1: IntArray, nums2: IntArray, queries: Array<IntArray>): LongArray {val n = nums1.sizeval resultList = LinkedList<Long>()// 全体和var sum = 0Lfor (num in nums2) {sum += num}val tree = SegementTree(nums1)for (query in queries) {when (query[0]) {1 -> {// 区间更新tree.update(query[1], query[2])}2 -> {// 求区间和(nums[index] * p)sum += 1L * query[1] * tree.query(0, n - 1)}3 -> {// 记录resultList.add(sum)}}}return resultList.toLongArray()}private class SegementTree(private val data: IntArray) {// 区间更新(反转)fun update(left: Int, right: Int) {}// 单点更新(反转)- 本题不需要fun set(pos: Int) {}// 区间查询fun query(left: Int, right: Int): Int {}}
}
接下来就是实现线段树的内部代码了。
- 技巧 1:这道题的更新操作是对 0/ 1 反转,我们可以用异或来实现;
- 技巧 2:相对于在函数中重复传递节点所代表的区间范围(例如
update(i: int, l: int, r: int, L: int, R: int)),使用 Node 节点记录更为方便。
class Solution {fun handleQuery(nums1: IntArray, nums2: IntArray, queries: Array<IntArray>): LongArray {val n = nums1.sizeval resultList = LinkedList<Long>()// 全体和var sum = 0Lfor (num in nums2) {sum += num}val tree = SegementTree(nums1)for (query in queries) {when (query[0]) {1 -> {// 区间更新tree.update(query[1], query[2])}2 -> {// 求区间和(nums[index] * p)sum += 1L * query[1] * tree.query(0, n - 1)}3 -> {// 记录resultList.add(sum)}}}return resultList.toLongArray()}private class SegementTree(private val data: IntArray) {// 线段树节点(区间范围与区间值)private class Node(val left: Int, val right: Int, var value: Int)// 线段树数组private val tree = Array<Node?>(4 * data.size) { null } as Array<Node>// 左子节点的索引private val Int.left get() = this * 2 + 1// 右子节点的索引private val Int.right get() = this * 2 + 2init {// 建树buildNode(0, 0, data.size - 1)}// 构建线段树节点private fun buildNode(index: Int, left: Int, right: Int) {if (left == right) {// 叶子节点tree[index] = Node(left, right, data[left])return}val mid = (left + right) ushr 1// 构建左子节点buildNode(index.left, left, mid)// 构建左子节点buildNode(index.right, mid + 1, right)// 合并左右子节点tree[index] = Node(left, right, tree[index.left].value + tree[index.right].value)}// 区间更新(反转)fun update(left: Int, right: Int) {update(0, left, right)}// 区间更新(反转)private fun update(index: Int, left: Int, right: Int) {// 1、当前节点不处于区间范围内if (tree[index].left > right || tree[index].right < left) return// 2、叶子节点if (tree[index].left == tree[index].right) {// 反转:0->1,1->0tree[index].value = tree[index].value xor 1return}// 3、更新左子树update(index.left, left, right)// 4、更新右子树update(index.right, left, right)// 5、合并子节点的结果tree[index].value = tree[index.left].value + tree[index.right].value}// 单点更新(反转)- 本题不需要fun set(pos: Int) {set(0, pos)}// 单点更新(反转)- 本题不需要private fun set(index: Int, pos: Int) {// 1、当前节点不处于区间范围内if (tree[index].left > pos || tree[index].right < pos) return// 2、叶子节点if (tree[index].left == tree[index].right) {// 反转:0->1,1->0tree[index].value = tree[index].value xor 1return}// 3、更新左子树set(index.left, pos)// 4、更新右子树set(index.right, pos)// 5、合并子节点的结果tree[index].value = tree[index.left].value + tree[index.right].value}// 区间查询fun query(left: Int, right: Int): Int {return query(0, left, right)}// 区间查询private fun query(index: Int, left: Int, right: Int): Int {// 1、当前节点不处于区间范围内if (tree[index].left > right || tree[index].right < left) return 0// 2、当前节点完全处于区间范围之内if (tree[index].left >= left && tree[index].right <= right) return tree[index].value// 3、合并子节点的结果return query(index.left, left, right) + query(index.right, left, right)}}
}
复杂度分析:
- 时间复杂度:O(n+q1n+q2)O(n + q_1n + q_2)O(n+q1n+q2) 其中 n 是 nums1 数组长度,q1q_1q1 是操作一的个数,q2q_2q2 是操作二的个数。我们需要花费 O(n)O(n)O(n) 时间建树,操作一线段树区间更新的时间复杂度是 O(n)O(n)O(n),操作二线段树区间查询的复杂度是 O(lgn)O(lgn)O(lgn),但本题中的查询正好是线段树根节点,所以操作二实际上只需要 O(1)O(1)O(1) 复杂度。
- 空间复杂度:O(n)O(n)O(n) 线段树空间。
朴素线段树解法在本题中会超时,我们需要优化为 “懒更新” 的线段树实现。
题解二(线段树 + 懒更新)
朴素线段树的性能瓶颈在于:区间更新需要改动从根节点到叶子节点中所有与目标区间有交集的节点,因此单次区间更新操作的时间复杂度是 O(n)O(n)O(n)。
懒更新线段树的核心思想是:当一个节点代表的区间完全包含于目标区间内时,我们没有必要继续向下递归更新,而是在当前节点上标记 Lazy Tag 。只有将来更新该节点的某个子区间时,才会将懒更新 pushdown 到子区间。
举个例子:在长度为 10 的线段树中执行 [1,10] 和 [1,5] 两次区间更新操作(对区间内的元素加一):
[1,10]区间更新:从根节点出发,此时发现根节点与目标区间[1,10]完全相同,那么只更新根节点并标记 Lazy Tag,更新结束;[1,5]区间更新:从根节点出发,此时发现根节点有 Lazy Tag,那么需要先将懒更新 pushdown 到[1,5]和[6,10]两个子节点,然后再更新[1,5]区间。- 到目前为止,
[1,10]和[1,5]节点被修改 2 次,[6,10]节点被修改 1 次,其它节点没有被修改。
接下来就是实现线段树的内部代码了。
- 技巧 1:0 /1 反转是负负得正的,所以 Lazy Tag 可以用
Boolean类型表示,true表示被反转; - 技巧 2:区间反转可以用区间长度 - 旧值实现,即:
value = right - left + 1 - value。
提示:相比题解一改动的函数有 【懒更新】 标记 。
class Solution {fun handleQuery(nums1: IntArray, nums2: IntArray, queries: Array<IntArray>): LongArray {val n = nums1.sizeval resultList = LinkedList<Long>()// 全体和var sum = 0Lfor (num in nums2) {sum += num}val tree = LazySegementTree(nums1)for (query in queries) {when (query[0]) {1 -> {// 区间更新tree.update(query[1], query[2])}2 -> {// 求区间和(nums[index] * p)sum += 1L * query[1] * tree.query(0, n - 1)}3 -> {// 记录resultList.add(sum)}}}return resultList.toLongArray()}private class LazySegementTree(private val data: IntArray) {// 线段树节点(区间范围与区间值)【懒更新】private class Node(val left: Int, val right: Int, var value: Int, var lazy: Boolean = false)// 线段树数组private val tree = Array<Node?>(4 * data.size) { null } as Array<Node>// 左子节点的索引private val Int.left get() = this * 2 + 1// 右子节点的索引private val Int.right get() = this * 2 + 2init {// 建树buildNode(0, 0, data.size - 1)}// 构建线段树节点private fun buildNode(index: Int, left: Int, right: Int) {if (left == right) {// 叶子节点tree[index] = Node(left, right, data[left])return}val mid = (left + right) ushr 1// 构建左子节点buildNode(index.left, left, mid)// 构建左子节点buildNode(index.right, mid + 1, right)// 合并左右子节点tree[index] = Node(left, right, tree[index.left].value + tree[index.right].value)}// 区间更新(反转)fun update(left: Int, right: Int) {update(0, left, right)}// 区间更新(反转)【懒更新】private fun update(index: Int, left: Int, right: Int) {// 1、当前节点不处于区间范围内if (tree[index].left > right || tree[index].right < left) return// 2、当前节点完全处于区间范围之内if (tree[index].left >= left && tree[index].right <= right) {lazyUpdate(index)return}// 3、pushdown 到子节点if (tree[index].lazy) {lazyUpdate(index.left)lazyUpdate(index.right)tree[index].lazy = false}// 4、更新左子树update(index.left, left, right)// 5、更新右子树update(index.right, left, right)// 6、合并子节点的结果tree[index].value = tree[index.left].value + tree[index.right].value}// 单点更新(反转)- 本题不需要fun set(pos: Int) {set(0, pos)}// 单点更新(反转)【懒更新】- 本题不需要private fun set(index: Int, pos: Int) {// 1、当前节点不处于区间范围内if (tree[index].left > pos || tree[index].right < pos) return// 2、叶子节点if (tree[index].left == tree[index].right) {lazyUpdate(index)return}// 3、pushdown 到子节点if (tree[index].lazy) {lazyUpdate(index.left)lazyUpdate(index.right)tree[index].lazy = false}// 4、更新左子树set(index.left, pos)// 5、更新右子树set(index.right, pos)// 6、合并子节点的结果tree[index].value = tree[index.left].value + tree[index.right].value}// 区间查询fun query(left: Int, right: Int): Int {return query(0, left, right)}// 区间查询private fun query(index: Int, left: Int, right: Int): Int {// 1、当前节点不处于区间范围内if (tree[index].left > right || tree[index].right < left) return 0// 2、当前节点完全处于区间范围之内if (tree[index].left >= left && tree[index].right <= right) return tree[index].value// 3、pushdown 到子节点if (tree[index].lazy) {lazyUpdate(index.left)lazyUpdate(index.right)tree[index].lazy = false}// 4、合并子节点的结果return query(index.left, left, right) + query(index.right, left, right)}// 懒更新private fun lazyUpdate(index: Int) {// 反转tree[index].value = tree[index].right - tree[index].left + 1 - tree[index].value// 标记(负负得正)tree[index].lazy = !tree[index].lazy}}
}
复杂度分析:
- 时间复杂度:O(n+q1lgn+q2)O(n + q_1lgn + q_2)O(n+q1lgn+q2) 其中 n 是 nums1 数组长度,q1q_1q1 是操作一的个数,q2q_2q2 是操作二的个数。
- 空间复杂度:O(n)O(n)O(n) 线段树空间。
相关文章:

LeetCode 双周赛 98,脑筋急转弯转不过来!
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。 大家好,我是小彭。 昨晚是 LeetCode 第 98 场双周赛,你参加了吗?这场周赛需要脑筋急转弯,转不过来 Medium 就会变成 Hard&#…...
函数的栈帧的创建和销毁
文章目录本章主题:一.什么是函数栈帧1.什么是栈2.什么是函数栈帧二.理解函数栈帧能解决什么问题呢?三.函数栈帧的创建和销毁解析1.预备知识(1) 认识相关寄存器和汇编指令(2)栈帧空间的维护2.解析函数栈帧的…...

python filtermapreducezip
一、filter 过滤 filter 过滤, 从可迭代对象中,筛选出满足条件的元素,再将这些满足条件的元素,组成一个新的可迭代对象。 方式一:filter(过滤方法,可迭代对象) 举例:将一个list中…...
Centos7搭建hadoop3.3.4分布式集群
文章目录1、背景2、集群规划2.1 hdfs集群规划2.2 yarn集群规划3、集群搭建步骤3.1 安装JDK3.2 修改主机名和host映射3.3 配置时间同步3.4 关闭防火墙3.5 配置ssh免密登录3.5.1 新建hadoop部署用户3.5.2 配置hadoopdeploy用户到任意一台机器都免密登录3.7 配置hadoop3.7.1 创建目…...

骨传导耳机工作原理,骨传导耳机优缺点
骨传导耳机虽说最近是十分火爆的一款单品,但还是有很多人对骨传导耳机不是很了解,骨传导耳机更多使用场景还是在户外运动使用,骨传导耳机对于长时间使用耳机的人来说十分友好,这主要还是得益于骨传导耳机传输声音的特殊性。 下面我…...
IDEA高效插件和设置
安装好Intellij idea之后,进行如下的初始化操作,工作效率提升十倍。 一. 安装插件 1. Codota 代码智能提示插件 只要打出首字母就能联想出一整条语句,这也太智能了,还显示了每条语句使用频率。 原因是它学习了我的项目代码&…...
Linux之网络流量监控工具ntopng YUM安装
一、ntopng简介 Ntop是一种监控网络流量工具,用ntop显示网络的使用情况比其他一些网络管理软件更加直观、详细。Ntop甚至可以列出每个节点计算机的网络带宽利用率。他是一个灵活的、功能齐全的,用来监控和解决局域网问题的工具;尤其当ntop与n…...
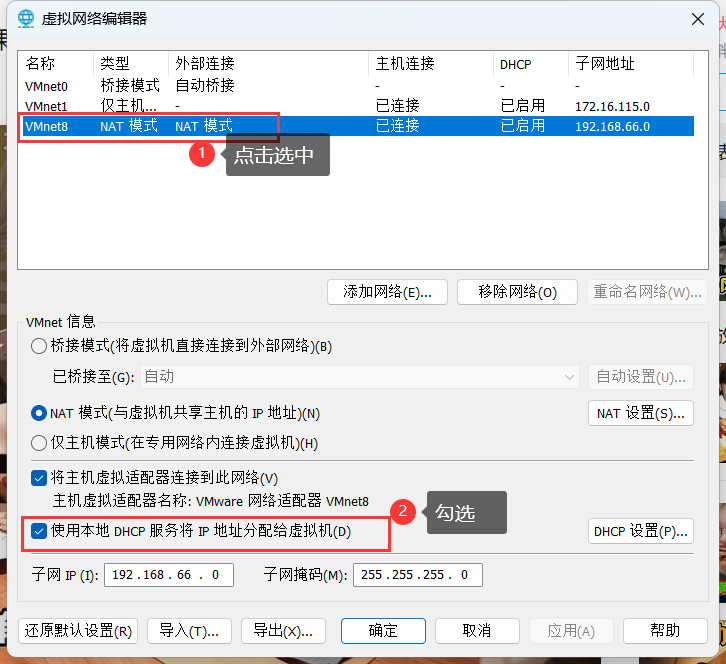
创建虚拟机,安装CentOS
在VMware上面创建虚拟机 文件->新建虚拟机 选定 自定义的高级,下一步 下一步 检查选定稍后安装操作系统 下一步 选择Linux,CentOS 7 64位 创建虚拟机名称,以及在存放该虚拟机的位置 选择处理器的数量和每个处理器的内核数量 …...
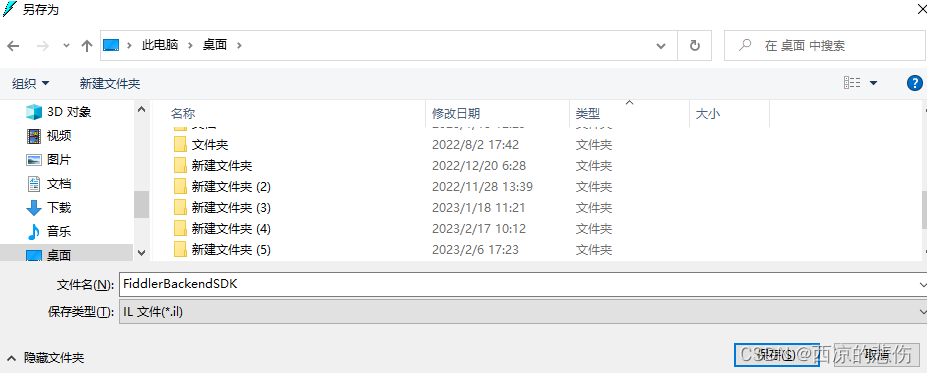
ilasm 和 ildasm编译和反编译工具介绍使用教程
目录前言一、使用 ildasm 反编译 dll 文件二、使用 ilasm 将il文件编译成 dll 或 exe 文件前言 文本讲述怎么通过 ildasm 工具将 dll 文件进行反编译为 il 文件,修改 il 文件后再如何通过 ilasm 工具将 il 文件反编译成 dll 或 exe 文件。 ildasm工具:…...

代码随想录【Day20】| 654. 最大二叉树、617. 合并二叉树、700. 二叉搜索树中的搜索、98. 验证二叉搜索树
654. 最大二叉树 题目链接 题目描述: 给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下: 二叉树的根是数组中的最大元素。 左子树是通过数组中最大值左边部分构造出的最大二叉树。 右子树是通过数组中最大值右边部分构造出的最…...
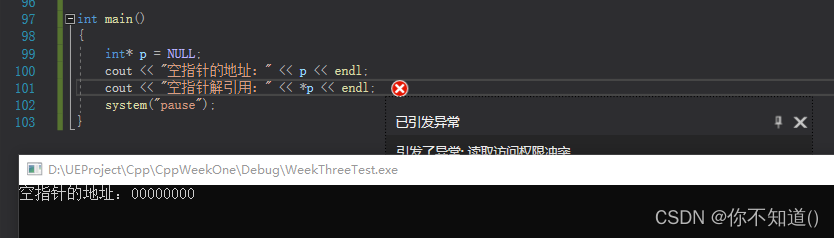
C++空指针和野指针
空指针:指针被赋值为空 例如: int* p nullptr;int* p NULL; 空指针指向的地址是00000000,但空指针不可以解引用 野指针:指针指向了不可控的位置 例如: 未初始化 int* p; //野指针 越界访问 int intArr[5]{0, 1, …...
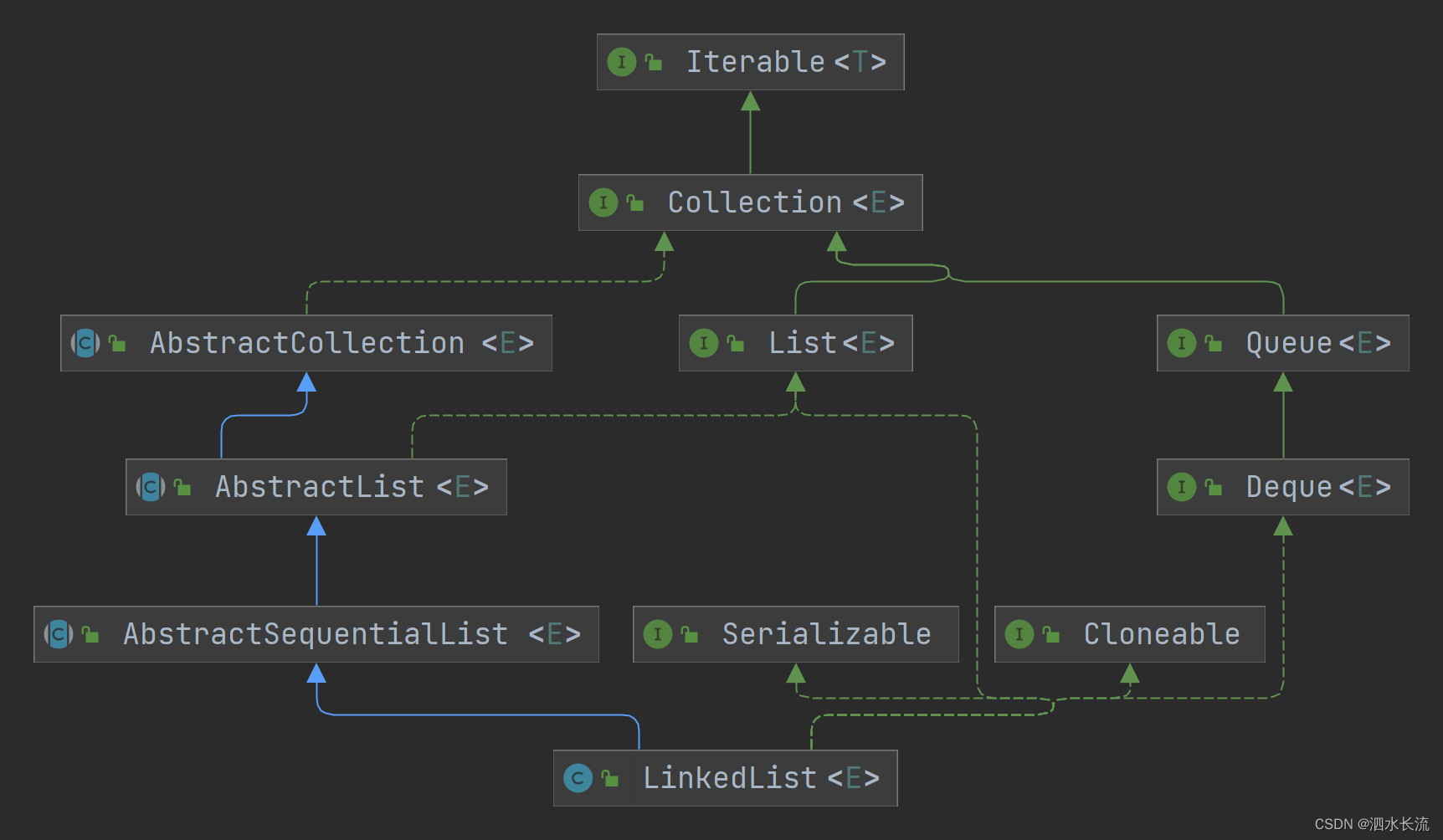
LinkedList正确的遍历方式-附源码分析
1.引子 记得之前面试过一个同学,有这么一个题目: LinkedList<String> list new LinkedList<>();for (int i 0; i < 1000; i) {list.add(i "");}请根据上面的代码,请选择比较恰当的方式遍历这个集合,并…...
【蓦然回首忆Java·基础卷Ⅱ】
文章目录对象内存解析方法的参数传递机制关键字:package、importpackage(包)JDK中主要的包介绍import(导入)JavaBeanUML类图继承的一些细节封装性中的4种权限修饰关键字:supersuper的理解super的使用场景子类中调用父类被重写的方法子类中调用父类中同名…...
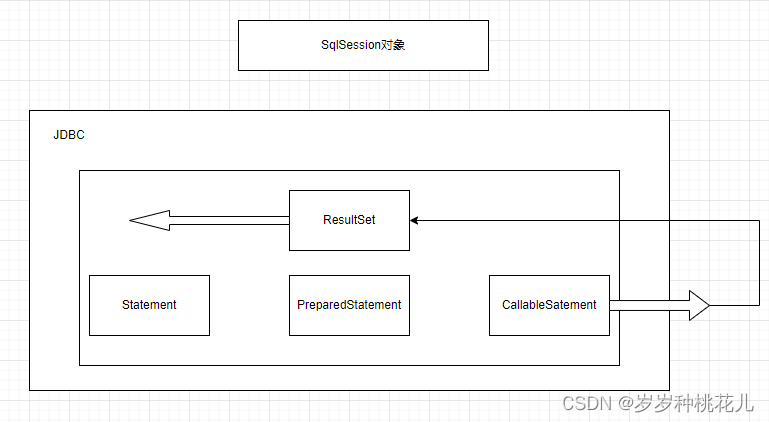
Mybatis源码分析系列之第二篇:Mybatis的数据存储对象
前言:SQLSession是对JDBC的封装 一:SQLSession和JDBC的对照说明 左边是我们的客户端程序,右边是我们的MySQL数据仓,或者叫MySQL实例 Mybatis是对JDBC的封装,将JDBC封装成了一个核心的SQLSession对象 JDBC当中的核心对…...

防护设备检测实验室建设完整方案SICOLAB
防护设备检测实验室建造布局方案SICOLAB一、防护设备检测实验室通常需要划分为几个功能区域,包括:1、样品准备区:用于样品的接收、处理、准备等工作,通常包括样品接收台、洗手池、样品切割机等设备。2、实验操作区:用于…...
Linux知识之主机状态
1、查看系统资源占用 •可以通过top命令查看CPU、内存使用情况,类似Windows的任务管理器默认每5秒刷新一次,语法:直接输入top即可,按q或ctrl c退出 2、 top命令内容详解 •第一行:top:命令名称࿰…...

是时候为您的银行机构选择构建一个知识库了!
知识管理和自助服务客户支持在银行业至关重要。选择正确的知识库对于帮助客户和在内部共享信息同样重要。繁重的法规和合规性需求意味着银行必须在他们选择的知识库类型上投入大量思考。许多银行知识库已经过时,无法为客户提供成功使用您的产品和服务所需的信息。在…...
「TCG 规范解读」第7章 TPM工作组 TPM 总结
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...

一、Plugin Constructing the Boilerplate
构建样板文件 在本章中,你将学习如何为一个新插件构建最少的代码。从起点开始,您将看到如何获取GStreamer模板源代码。然后,您将学习如何使用一些基本工具来复制和修改模板插件,以创建一个新的插件。如果您遵循这里的示例&#x…...

15、存储过程与函数
文章目录1 存储过程概述1.1 理解1.2 分类2 创建存储过程2.1 语法分析2.2 代码举例3 调用存储过程3.1 调用格式3.2 代码举例3.3 如何调试4 存储函数的使用4.1 语法分析4.2 调用存储函数4.3 代码举例4.4 对比存储函数和存储过程5 存储过程和函数的查看、修改、删除5.1 查看5.2 修…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
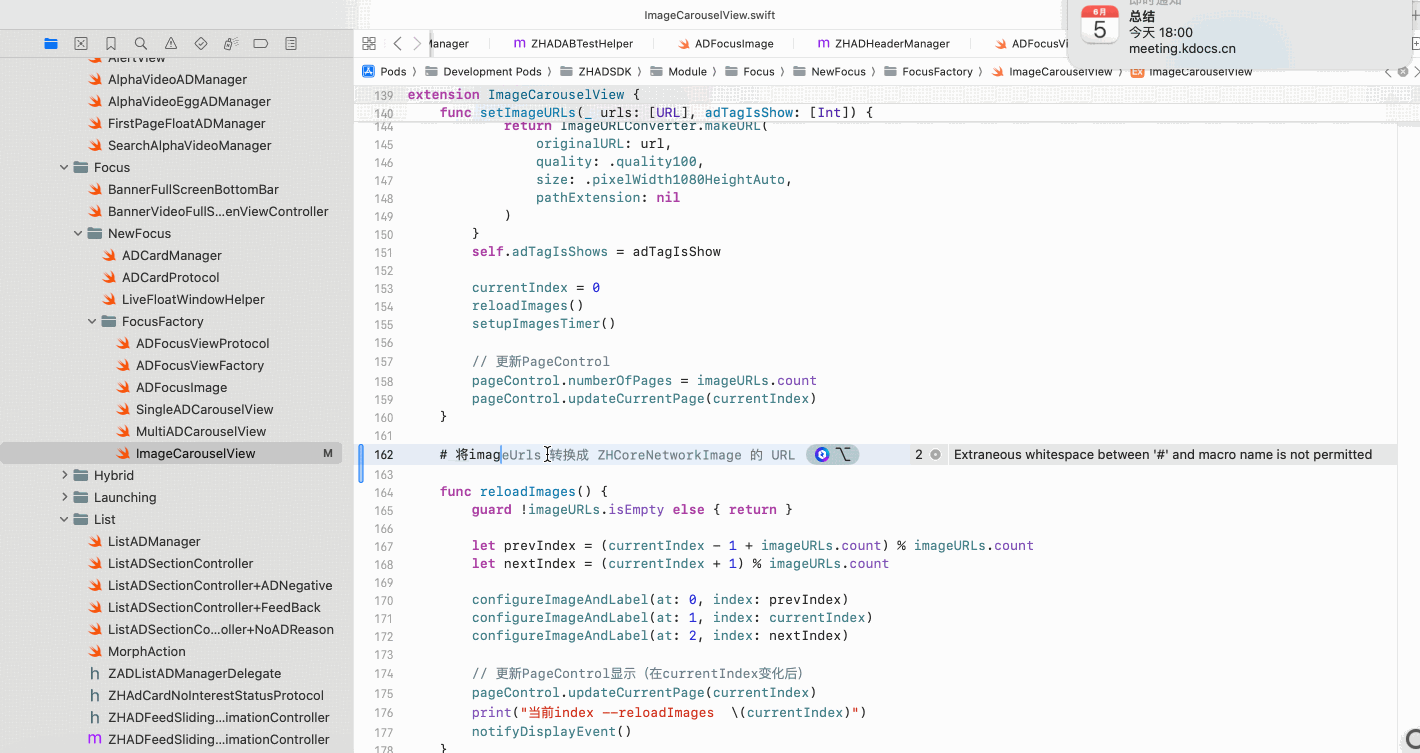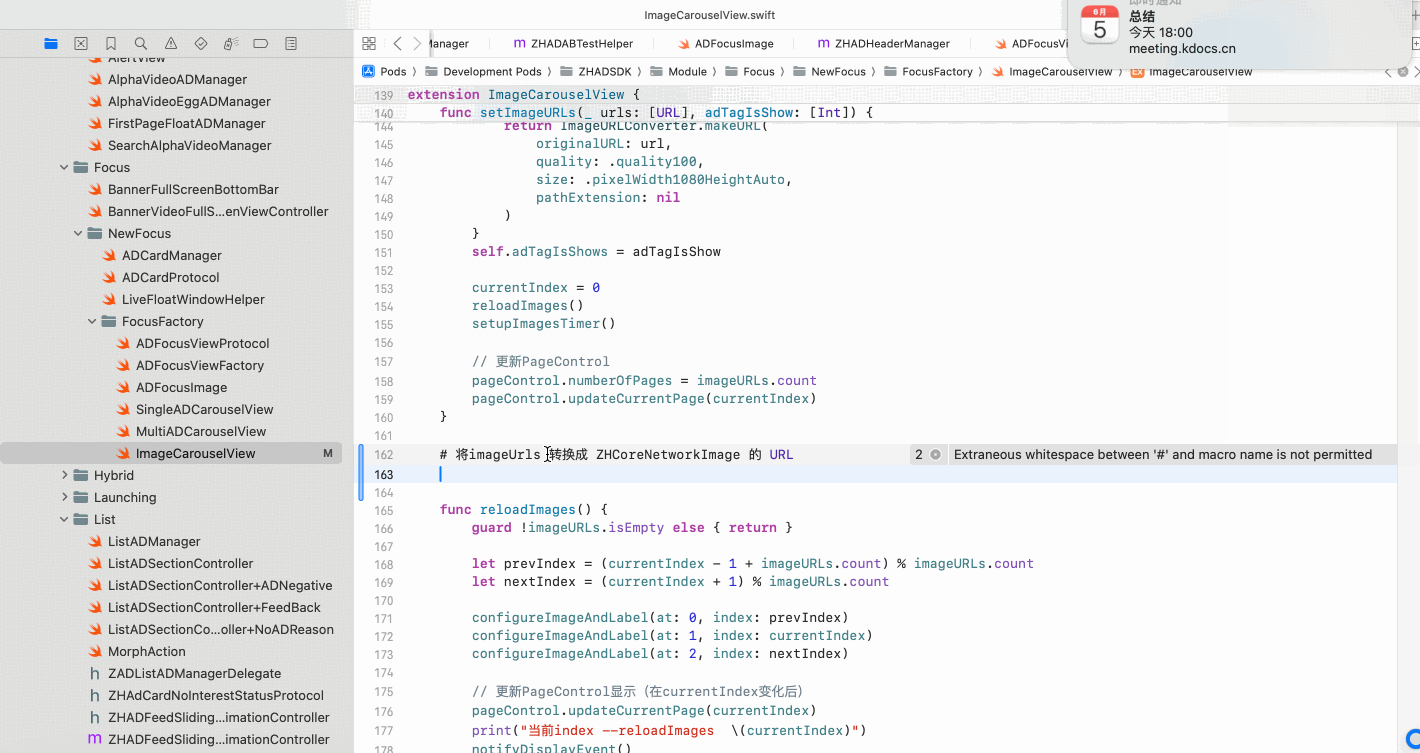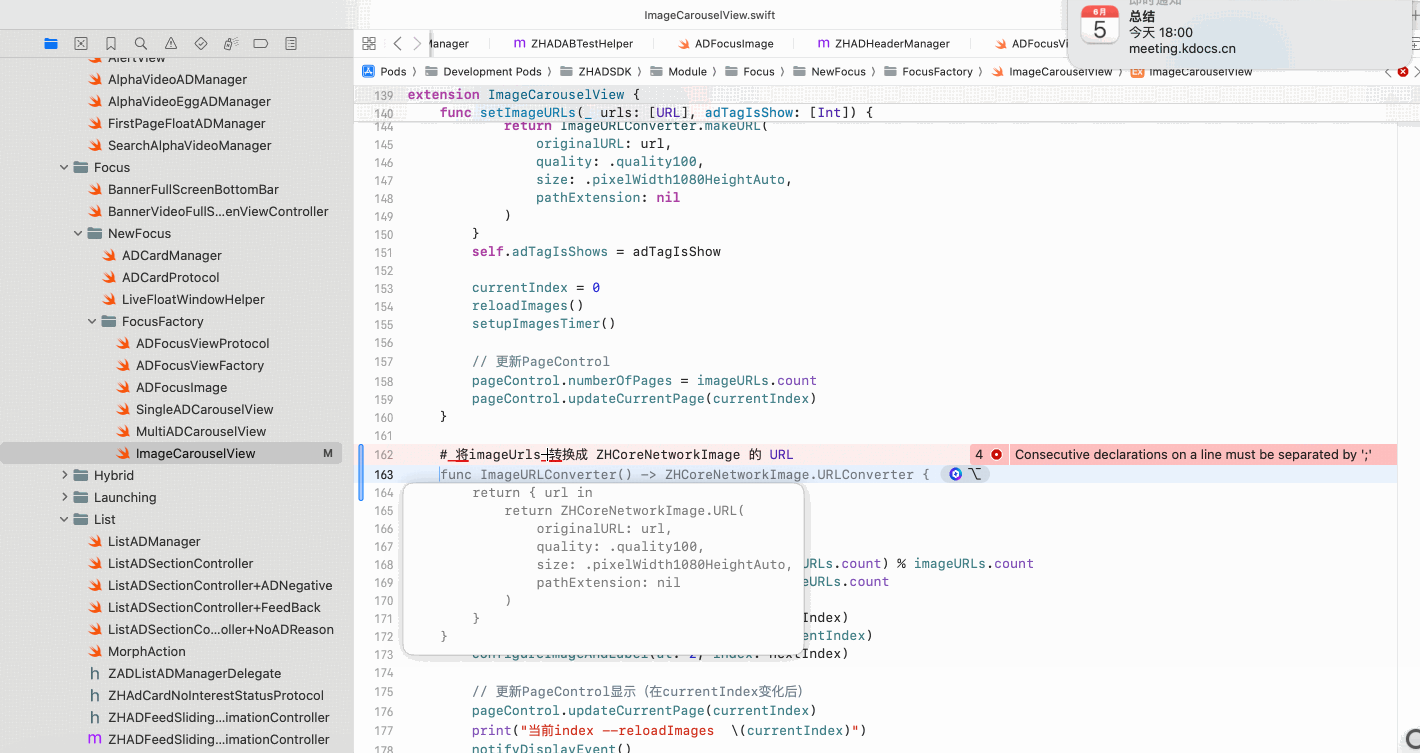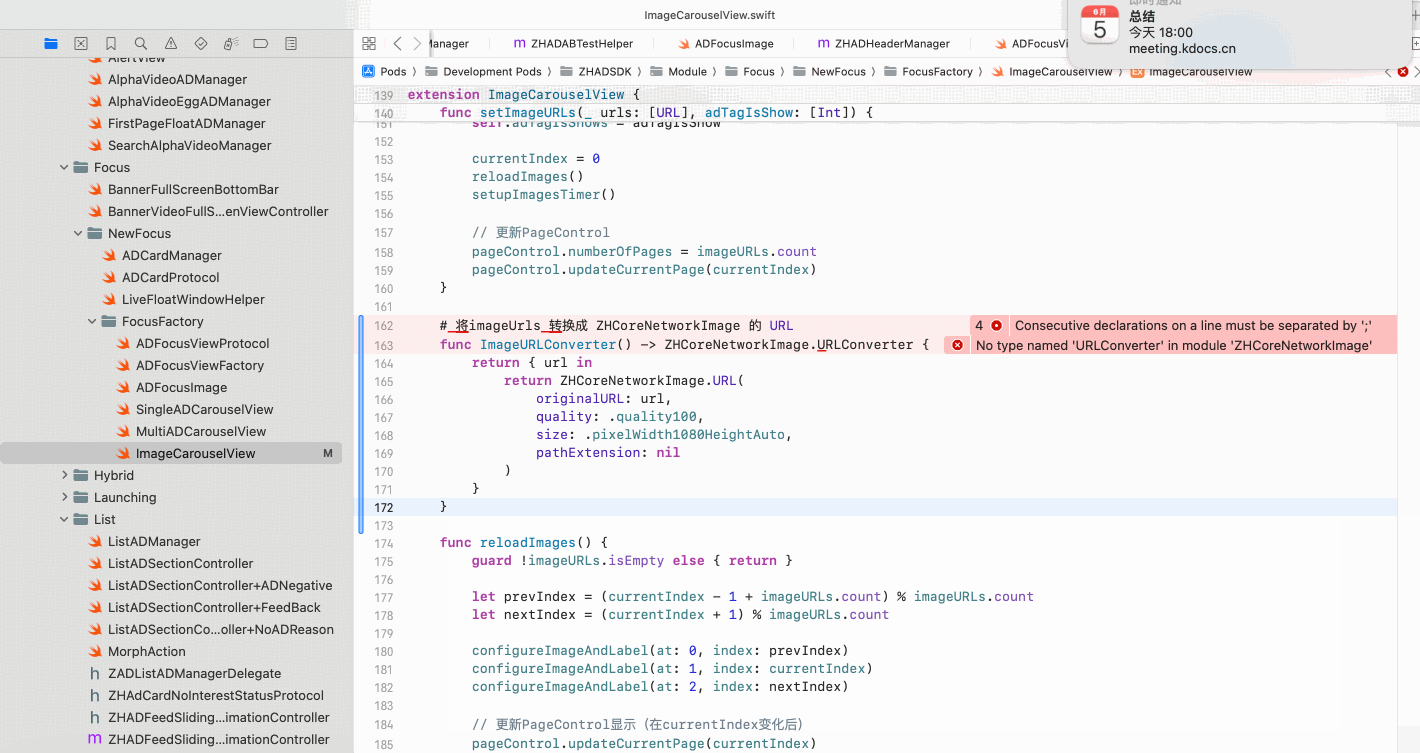
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...
