2023年高教社杯数学建模思路 - 案例:异常检测
文章目录
- 赛题思路
- 一、简介 -- 关于异常检测
- 异常检测
- 监督学习
- 二、异常检测算法
- 2. 箱线图分析
- 3. 基于距离/密度
- 4. 基于划分思想
- 建模资料
赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
一、简介 – 关于异常检测
异常检测(outlier detection)在以下场景:
- 数据预处理
- 病毒木马检测
- 工业制造产品检测
- 网络流量检测
等等,有着重要的作用。由于在以上场景中,异常的数据量都是很少的一部分,因此诸如:SVM、逻辑回归等分类算法,都不适用,因为:
监督学习算法适用于有大量的正向样本,也有大量的负向样本,有足够的样本让算法去学习其特征,且未来新出现的样本与训练样本分布一致。
以下是异常检测和监督学习相关算法的适用范围:
异常检测
- 信用卡诈骗
- 制造业产品异常检
- 数据中心机器异常检
- 入侵检测
监督学习
- 垃圾邮件识别
- 新闻分类
二、异常检测算法

import tushare
from matplotlib import pyplot as pltdf = tushare.get_hist_data("600680")
v = df[-90: ].volume
v.plot("kde")
plt.show()
近三个月,成交量大于200000就可以认为发生了异常(天量,嗯,要注意风险了……)
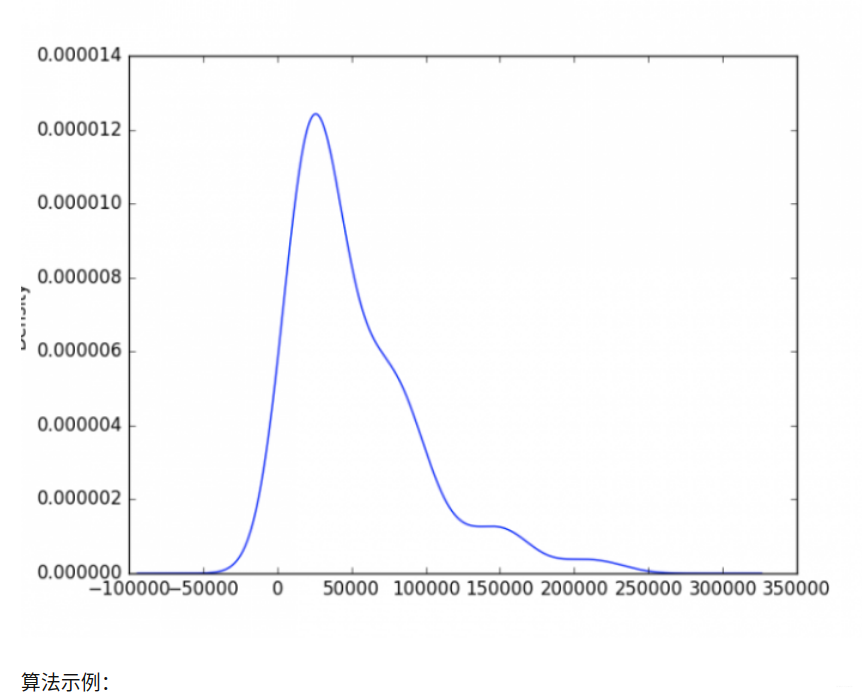

2. 箱线图分析
import tushare
from matplotlib import pyplot as pltdf = tushare.get_hist_data("600680")
v = df[-90: ].volume
v.plot("kde")
plt.show()
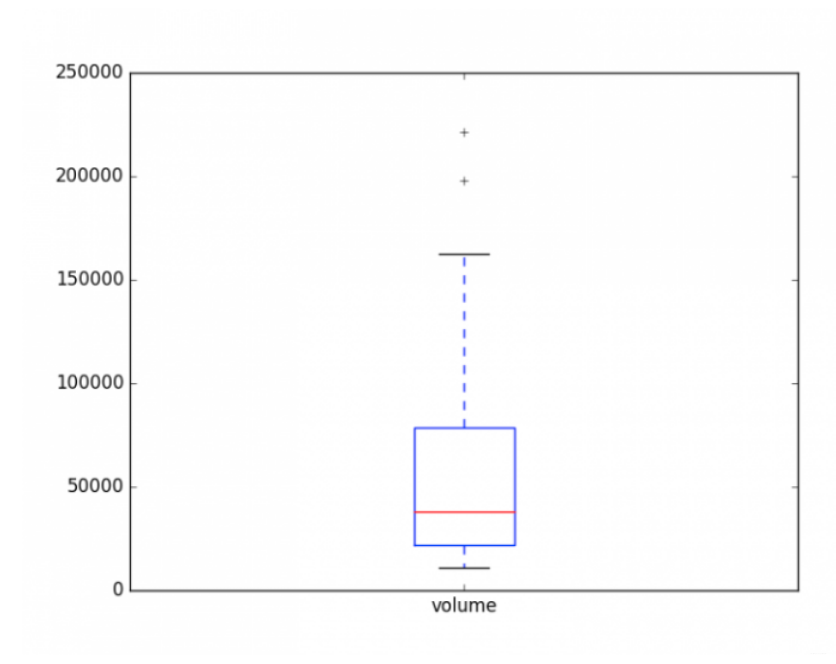
大体可以知道,该股票在成交量少于20000,或者成交量大于80000,就应该提高警惕啦!
3. 基于距离/密度
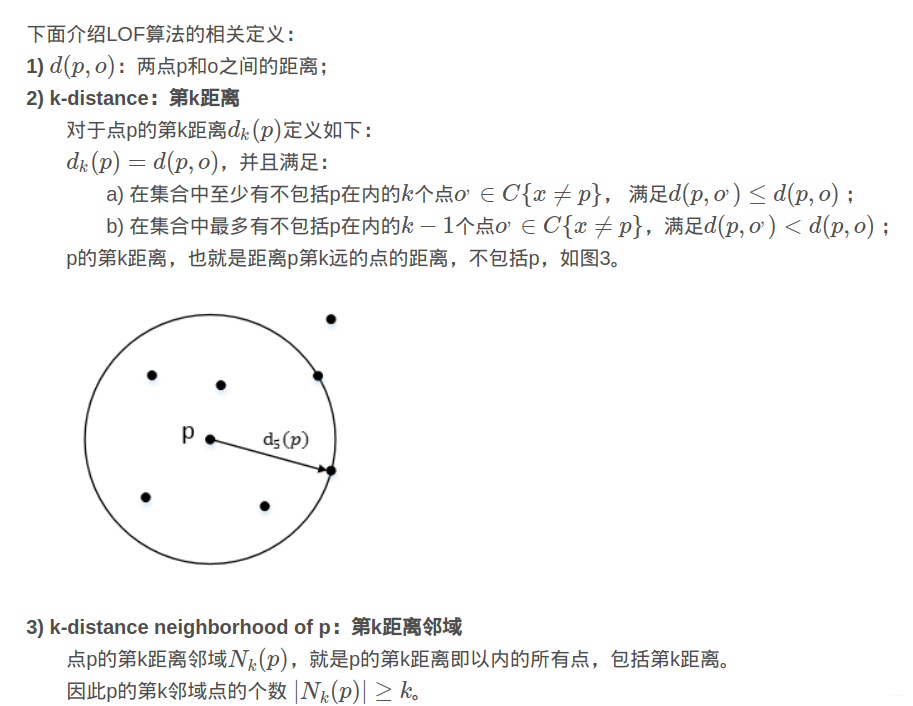
典型的算法是:“局部异常因子算法-Local Outlier Factor”,该算法通过引入“k-distance,第k距离”、“k-distance neighborhood,第k距离邻域”、“reach-distance,可达距离”、以及“local reachability density,局部可达密度 ”和“local outlier factor,局部离群因子”,来发现异常点。
用视觉直观的感受一下,如图2,对于C1集合的点,整体间距,密度,分散情况较为均匀一致,可以认为是同一簇;对于C2集合的点,同样可认为是一簇。o1、o2点相对孤立,可以认为是异常点或离散点。现在的问题是,如何实现算法的通用性,可以满足C1和C2这种密度分散情况迥异的集合的异常点识别。LOF可以实现我们的目标。

4. 基于划分思想
典型的算法是 “孤立森林,Isolation Forest”,其思想是:
假设我们用一个随机超平面来切割(split)数据空间(data space), 切一次可以生成两个子空间(想象拿刀切蛋糕一分为二)。之后我们再继续用一个随机超平面来切割每个子空间,循环下去,直到每子空间里面只有一个数据点为止。直观上来讲,我们可以发现那些密度很高的簇是可以被切很多次才会停止切割,但是那些密度很低的点很容易很早的就停到一个子空间了。
这个的算法流程即是使用超平面分割子空间,然后建立类似的二叉树的过程:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForestrng = np.random.RandomState(42)# Generate train data
X = 0.3 * rng.randn(100, 2)
X_train = np.r_[X + 1, X - 3, X - 5, X + 6]
# Generate some regular novel observations
X = 0.3 * rng.randn(20, 2)
X_test = np.r_[X + 1, X - 3, X - 5, X + 6]
# Generate some abnormal novel observations
X_outliers = rng.uniform(low=-8, high=8, size=(20, 2))# fit the model
clf = IsolationForest(max_samples=100*2, random_state=rng)
clf.fit(X_train)
y_pred_train = clf.predict(X_train)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)# plot the line, the samples, and the nearest vectors to the plane
xx, yy = np.meshgrid(np.linspace(-8, 8, 50), np.linspace(-8, 8, 50))
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.title("IsolationForest")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='green')
c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='red')
plt.axis('tight')
plt.xlim((-8, 8))
plt.ylim((-8, 8))
plt.legend([b1, b2, c],["training observations","new regular observations", "new abnormal observations"],loc="upper left")
plt.show()

建模资料
资料分享: 最强建模资料


相关文章:

2023年高教社杯数学建模思路 - 案例:异常检测
文章目录 赛题思路一、简介 -- 关于异常检测异常检测监督学习 二、异常检测算法2. 箱线图分析3. 基于距离/密度4. 基于划分思想 建模资料 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 一、简介 – 关于异常…...

C# Dapper 操作Oracle数据库
nuget安装内容 1.配置连接字符串 OracleConnectionString这个可用 {"Logging": {"LogLevel": {"Default": "Information","Microsoft.AspNetCore": "Warning"}},"AllowedHosts": "*","…...
element侧边栏子路由点击不高亮问题
最近自己封装侧边栏 又碰到了点击子路由不高亮的问题 <template><div class"aside"><el-scrollbar :vertical"true" class"scrollbar_left_nav"><el-menu :default-active"defaultActive" :collapse"$stor…...

C# 试图加载格式不正确的程序。 (异常来自 HRESULT:0x8007000B)
C# 在调用Cdll时,可能会出现 :试图加载格式不正确的程序。 (异常来自 HRESULT:0x8007000B)这个错误。 一般情况下是C#目标平台跟Cdll不兼容,64位跟32位兼容性问题, a.客户端调用Cdll报的错则, 1)允许的话把C#客户端…...

Linux 进程的睡眠和唤醒详解
概要 在Linux中,仅等待CPU时间的进程称为就绪进程,它们被放置在一个运行队列中,一个就绪进程的状 态标志位为 TASK_RUNNING。一旦一个运行中的进程时间片用完, Linux 内核的调度器会剥夺这个进程对CPU的控制权,并且从运…...

AI 绘画Stable Diffusion 研究(十五)SD Embedding详解
大家好,我是风雨无阻。 本期内容: Embedding是什么?Embedding有什么作用?Embedding如何下载安装?如何使用Embedding? 大家还记得 AI 绘画Stable Diffusion 研究(七) 一文读懂 Stab…...
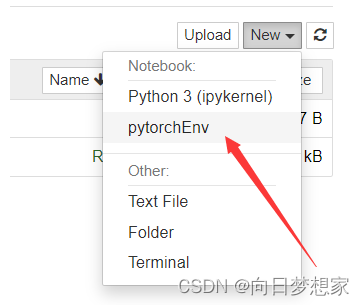
在Jupyter Notebook中添加Anaconda环境(内核)
在使用前我们先要搞清楚一些事: 我们在安装anaconda的时候它就内置了Jupyter Notebook,这个jupyter初始只有base一个内核(显示为Python3) 此后其实我们就不需要重复安装完整的jupyter notebook了,只要按需为其添加新的…...

适配器模式简介
概念: 适配器模式(Adapter Pattern)是一种结构型设计模式,用于将一个类的接口转换成客户端所期望的另一个接口。它允许不兼容的接口之间进行协同工作。 特点: 通过适配器,可以使原本因为接口不匹配而无法…...

MyBatis —— 多种查询及映射关系
前言 上一篇文章中荔枝梳理了有关MyBatis的相关环境配置和核心配置文件及其模板的设置和生成,而在这篇文章中荔枝会着重梳理MyBatis多种查询情况、特殊SQL执行以及两表联查时映射关系的处理。希望对需要的小伙伴有帮助~~~ 文章目录 前言 一、多种查询情况 1.1 查…...

腾讯云服务器镜像TencentOS Server操作系统详细介绍
腾讯云TencentOS Server镜像是腾讯云推出的Linux操作系统,完全兼容CentOS生态和操作方式,TencentOS Server操作系统为云上运行的应用程序提供稳定、安全和高性能的执行环境,TencentOS可以运行在腾讯云CVM全规格实例上,包括黑石物理…...
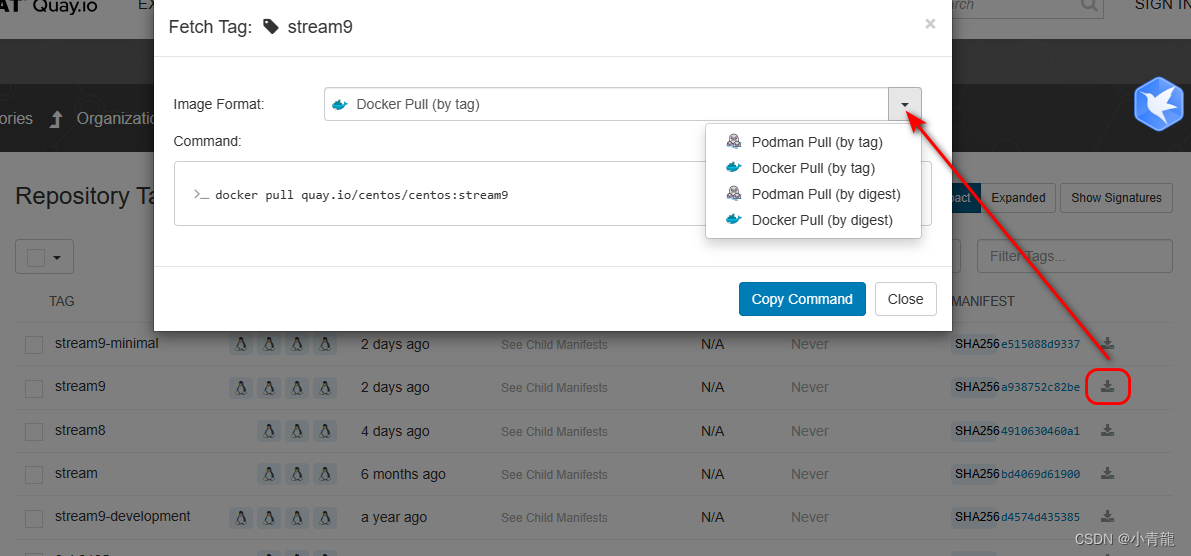
Docker 中下载各版本的 CentOS、CentOS Steam 方式
如果你跟我一样,想要在docker下载centos的镜像,但是无奈访问不了 https://hub.docker.com/,于是不知道有哪些tag可以下载,该如何办呢? 方法如下,以供参考。 访问:https://quay.io/repository/…...
多线程使用HashMap,HashMap和HashTable和ConcurrentHashMap区别(面试题常考),硬盘IO,顺便回顾volatile
一、回顾💛 谈谈volatile关键字用法 volatile能够保证内存可见性,会强制从主内存中读取数据,此时如果其他线程修改被volatile修饰的变量,可以第一时间读取到最新的值。 二、💙 HashMap线程不安全没有锁,HashTable线程…...

专线连接交换机设置 – 如何实现高效率的网络连接?
专线链接交换机设置 – 如何实现高效率的网络连接? 什么是专线连接交换机? 在现代互联网中,网络连接的快速和高效是至关重要的。尤其是对于需要大量数据传输和保证网络稳定性的企业和组织来说,专线连接交换机是一项非常重要的技…...

C#,数值计算——Midexp的计算方法与源程序
1 文本格式 using System; namespace Legalsoft.Truffer { public class Midexp : Midpnt { public new double func(double x) { return funk.funk(-Math.Log(x)) / x; } public Midexp(UniVarRealValueFun funcc, double aa, d…...
和wx.getStorageSync())
微信小程序使用本地存储方法wx.setStorageSync()和wx.getStorageSync()
微信小程序的本地存储可以使用wx.setStorageSync()和wx.getStorageSync()方法实现 使用wx.setStorageSync()方法可以将数据以键值对的方式存储到本地存储中: wx.setStorageSync(demo, demo123);获取数据:使用wx.getStorageSync()方法可以从本地存储中获…...

题解:ABC317C - Remembering the Days
题解:ABC317C - Remembering the Days 题目 链接:Atcoder。 链接:洛谷。 难度 算法难度:B。 思维难度:B。 调码难度:C。 综合评价:普及-。 算法 深度优先搜索。 思路 先建图&#x…...

【CSS】简记CSS效果:通过transition(动画过渡属性)实现侧边栏目滑入滑出
需求 在资金明细的页面中,点击按钮时筛选区域从左侧滑出,完成筛选点击确认后调用接口完成数据查询,筛选区域滑入左侧; 基于微信小程序页面实现 wxml代码 <view><!-- 操作按钮 --><button type"primary&qu…...
)
LeetCode——最大子数组和(中等)
题目 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,4] 输出&#x…...

Zookeeper集成SpringBoot
Curator 是 Apache ZooKeeper 的Java客户端库。 Zookeeper现有常见的Java API如:原生JavaAPI、Curator、ZkClient等。 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"…...
ModaHub魔搭社区:星环科技致力于打造更优越的向量数据库
在数字化时代,数据成为了最重要的资源之一。随着人工智能、大数据等技术的不断发展,向量数据库成为了处理这类数据的关键工具。星环科技作为一家专注于数据存储和管理技术的公司,其重要目标就是将向量数据库打造得更为优越。 在星环科技,有一个专注于向量数据库的团队。这个…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
