宏观经济和风电预测误差分析(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码、数据、详细文章
💥1 概述
本文包括以下几个部分,然后用Matlab代码实现之。


准确预测的发展和估计在许多行业和日常生活中具有特殊的重要性。对于政治和经济来说,提前了解宏观经济发展情况以确定其战略是很重要的。作为投资者,预测市场走势或利率是至关重要的,而对于良好的能源供应管理,提前了解可再生能源的产出是必要的。例如,美国为数百万电力客户提供服务的Xcel Energy Inc.将其预测误差率降低了35%,从而实现了对煤炭和天然气发电厂更加高效的管理。迄今为止,这节省了超过6000万美元。(Xcel Energy Inc. 2017a; Xcel Energy Inc. 2017b)。
为了提高预测的准确性,获取有关预测误差的知识是有用的。尽管先前的研究主要集中在绩效评估和实际时间序列的统计特性上,但本文关注的是预测误差的统计特性。目标是找到预测误差的典型事实。典型事实是对常见统计特性的简化抽象,由Kaldor(1961)首次引入。Cont(2001)在资产回报的范围内将典型事实定义为在“许多工具、市场和时间段”中普遍存在的统计特性。转移到本文中,我们寻找在许多预测方法、行业和时间段中普遍存在的统计特性。此外,我们区分行业,因为可能存在仅在单个行业中普遍存在的特性。为了做到这一点,我们将收集时间序列的特征和特性,并寻找共同点。此外,本文介绍了协整和误差修正模型的原理,并将其归类为预测误差的典型事实的范畴。
预测是利用现有信息对未来价值进行预测的过程。该过程包括对过去和现在的价值、趋势、季节效应等进行分析。
设yt表示最后一个可用值,yt+k|t表示预测值,那么时间段k被称为预测时段。换句话说,它是估计值和实际值之间的时间段。例如,提前24小时估计的预测值具有24小时的预测时段。随着预测时段的增加,预测过程变得更加复杂,因为在t时期可用的信息较少。
为了从预测误差中得出结论,了解预测是如何创建的很重要。我们介绍了一种直观的标准方法,并简要解释了实际预测的工作原理。
持续模型,也称为不变模型,是一种简单的方法,通常用作其他方法的基准模型。它也是几种预测误差度量的一部分。定义如方程1所示,其中yt+k|t表示预测值,yt表示最后一个实际值,k表示预测时段。
yt+k|t = yt (1)
简而言之,预测值就是最后一个实际值(B.-M. Hodge和Michael Milligan 2011)。
实际使用的预测模型通常是几种更复杂方法的组合。例如,风力预测模型通常与风速预测一起构建。德国输电系统运营商50Hertz使用来自各种研究机构的预测组合(50Hertz Transmission GmbH 2017)。在M3挑战赛和欧洲央行(ECB)的专业预测师调查中使用的一些预测方法包括自回归积分移动平均(ARIMA)模型、人工神经网络和指数平滑方法。
📚2 运行结果











运行结果比较多,就不一一展示。
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。

🌈4 Matlab代码、数据、详细文章
相关文章:

宏观经济和风电预测误差分析(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
GO学习之 搜索引擎(ElasticSearch)
GO系列 1、GO学习之Hello World 2、GO学习之入门语法 3、GO学习之切片操作 4、GO学习之 Map 操作 5、GO学习之 结构体 操作 6、GO学习之 通道(Channel) 7、GO学习之 多线程(goroutine) 8、GO学习之 函数(Function) 9、GO学习之 接口(Interface) 10、GO学习之 网络通信(Net/Htt…...

Sentinel —实时监控
Sentinel 提供对所有资源的实时监控。如果需要实时监控,客户端需引入以下依赖(以 Maven 为例): <dependency><groupId>com.alibaba.csp</groupId><artifactId>sentinel-transport-simple-http</artif…...
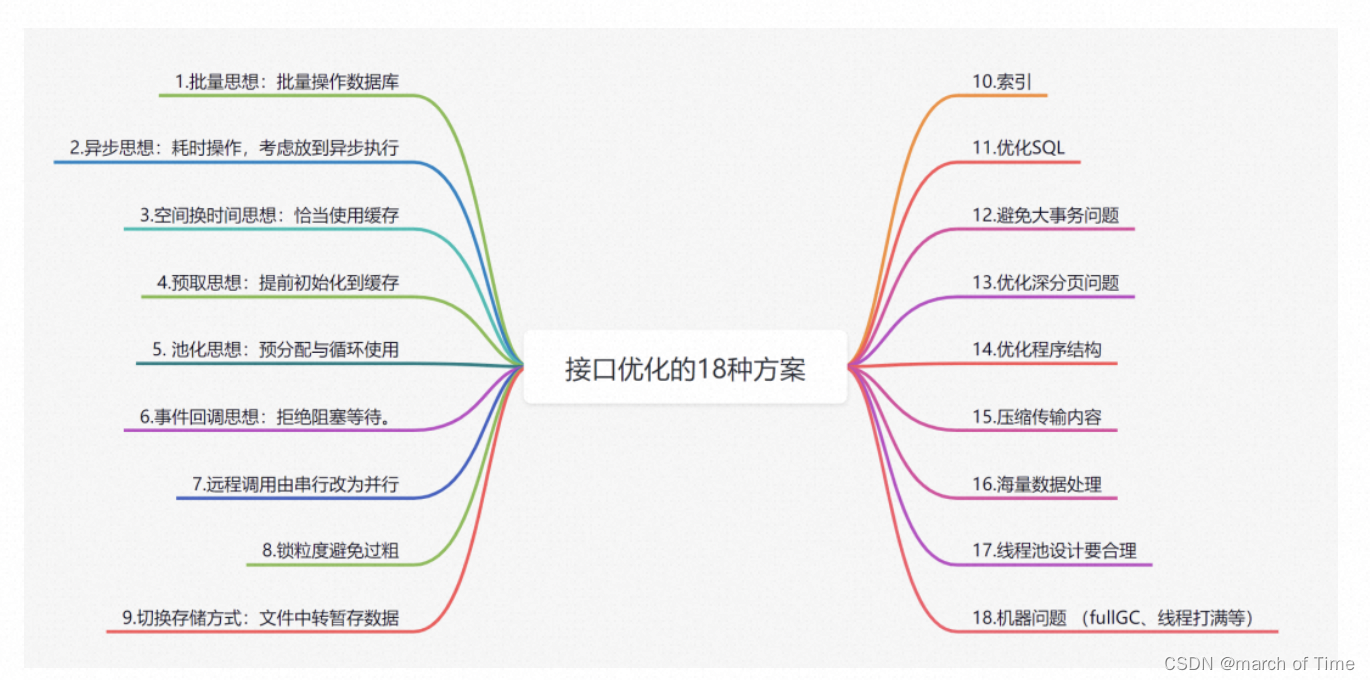
接口优化通用方案
目录 批量异步、回调缓存预取池化并行锁粒度索引大事务海量数据 批量 批量思想:批量操作数据库 优化前: //for循环单笔入库 for(TransDetail detail:transDetailList){ insert(detail); } 优化后: batchInsert(transDetailList); 异步、回…...

用Visual Studio 2022的.map文件来查看C++变量在内存中的布局情况
先看几个实例 代码1 #include <iostream> int data_arr[32768]; int main() {data_arr[1] 11;std::cout<<"data_arr[1]: " << data_arr[1] << std::endl;return data_arr[1]; } 上述代码在Win10 X64,MSVC Release模式下编译&…...
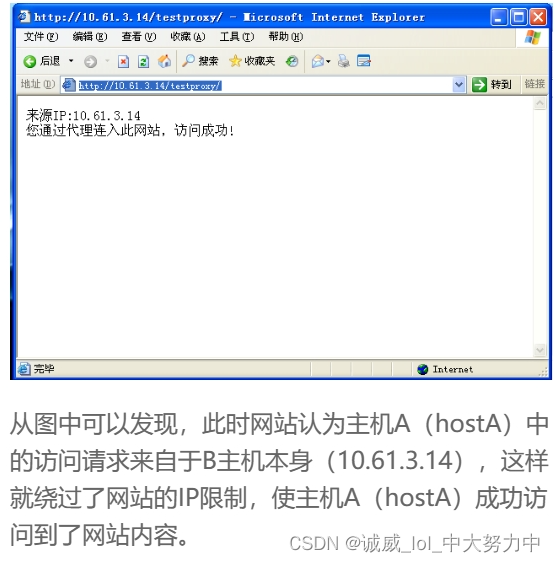
使用代理突破浏览器IP限制
一、实验目的: 主要时了解代理服务器的概念,同时如何突破浏览器IP限制 二、预备知识: 代理服务器英文全称是Proxy Server,其功能就是代理网络用户去取得网络信息。形象的说:它是网络信息的中转站,特别是它具有一个cac…...
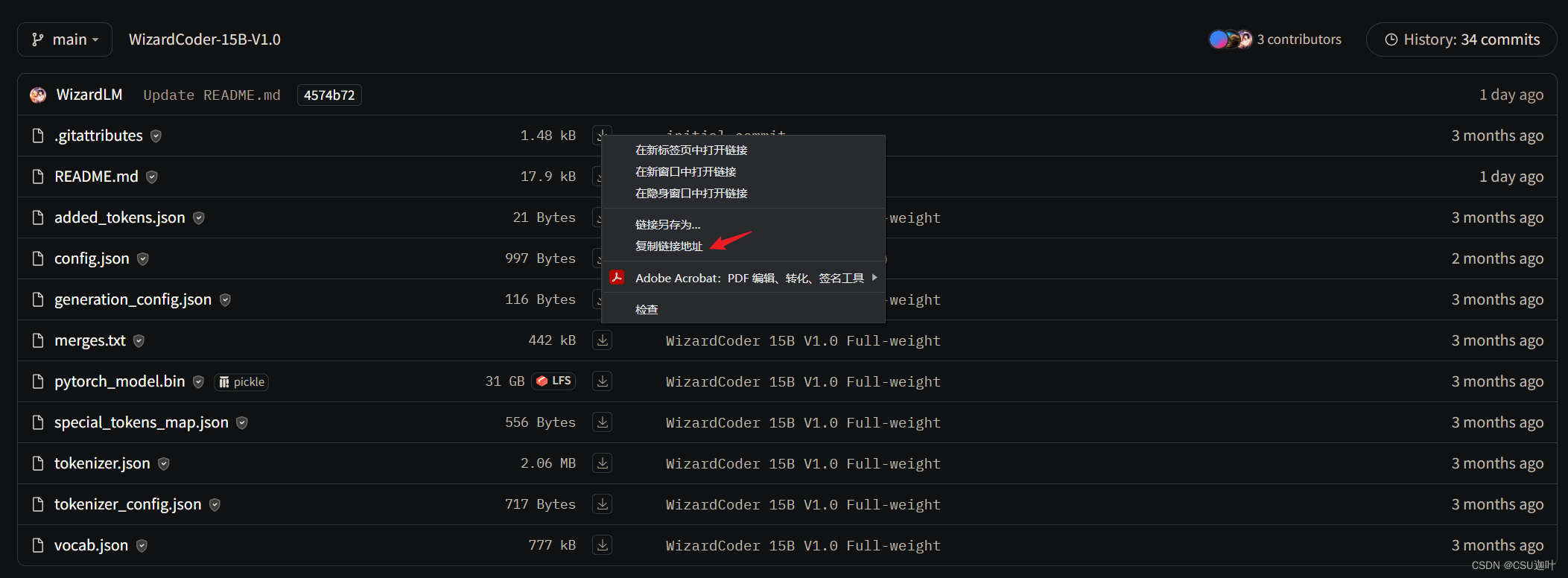
HuggingFace中的 Files and versions 如何优雅下载到本地?(Python requests,tqdm)
前言 在使用huggingface把玩各种大模型时,如果选择从远程加载模型,这个过程可能因为网络问题而非常耗时甚至直接失败,所以把模型、分词器等相关文件下载到本地,再直接从本地加载就成了不可回避的流程。 在进入具体版本的模型后&…...
三、原型模式
一、什么是原型模式 原型(Prototype)模式的定义如下:用一个已经创建的实例作为原型,通过复制该原型对象来创建一个和原型相同或相似的新对象。在这里,原型实例指定了要创建的对象的种类。用这种方式创建对象非常高效&a…...

transformer实现词性标注
1、self-attention 1.1、self-attention结构图 上图是 Self-Attention 的结构,在计算的时候需要用到矩阵 Q(查询), K(键值), V(值)。在实际中,Self-Attention 接收的是输入(单词的表示向量 x组成的矩阵 X) 或者上一个 Encoder block 的输出。而 Q, K, V…...

Java中异或操作和OTP算法
最近在研究加密算法,发现异或操作在加密算法中用途特别广,也特别好用。下面以Java语言为例,简单记录一下异或操作,以及在算法中的使用,包括常用的OTP算法。 一,异或操作特征 1, 相同出0&#…...
K8S最新版本集群部署(v1.28) + 容器引擎Docker部署(下)
温故知新 📚第三章 Kubernetes各组件部署📗安装kubectl(可直接跳转到安装kubeadm章节,直接全部安装了)📕下载kubectl安装包📕执行kubectl安装📕验证kubectl 📗安装kubead…...

女子垒球运动的发展·垒球1号位
女子垒球运动的发展 1. 女子垒球运动的起源和发展概述 女子垒球运动,诞生于19世纪末的美国,作为棒球运动的衍生品,经过百年的积淀,已在全球范围内广泛传播,形成了丰富的赛事文化。她的起源,可以追溯到19世…...

Debian 30 周年,生日快乐!
导读近日是 Debian 日,也是由伊恩-默多克(Ian Murdock)创立的 Debian GNU/Linux 通用操作系统和社区支持的 Debian 项目 30 周年纪念日。 不管你信不信,从已故的伊恩-默多克于 1993 年 8 月 16 日宣布成立 Debian 项目,…...
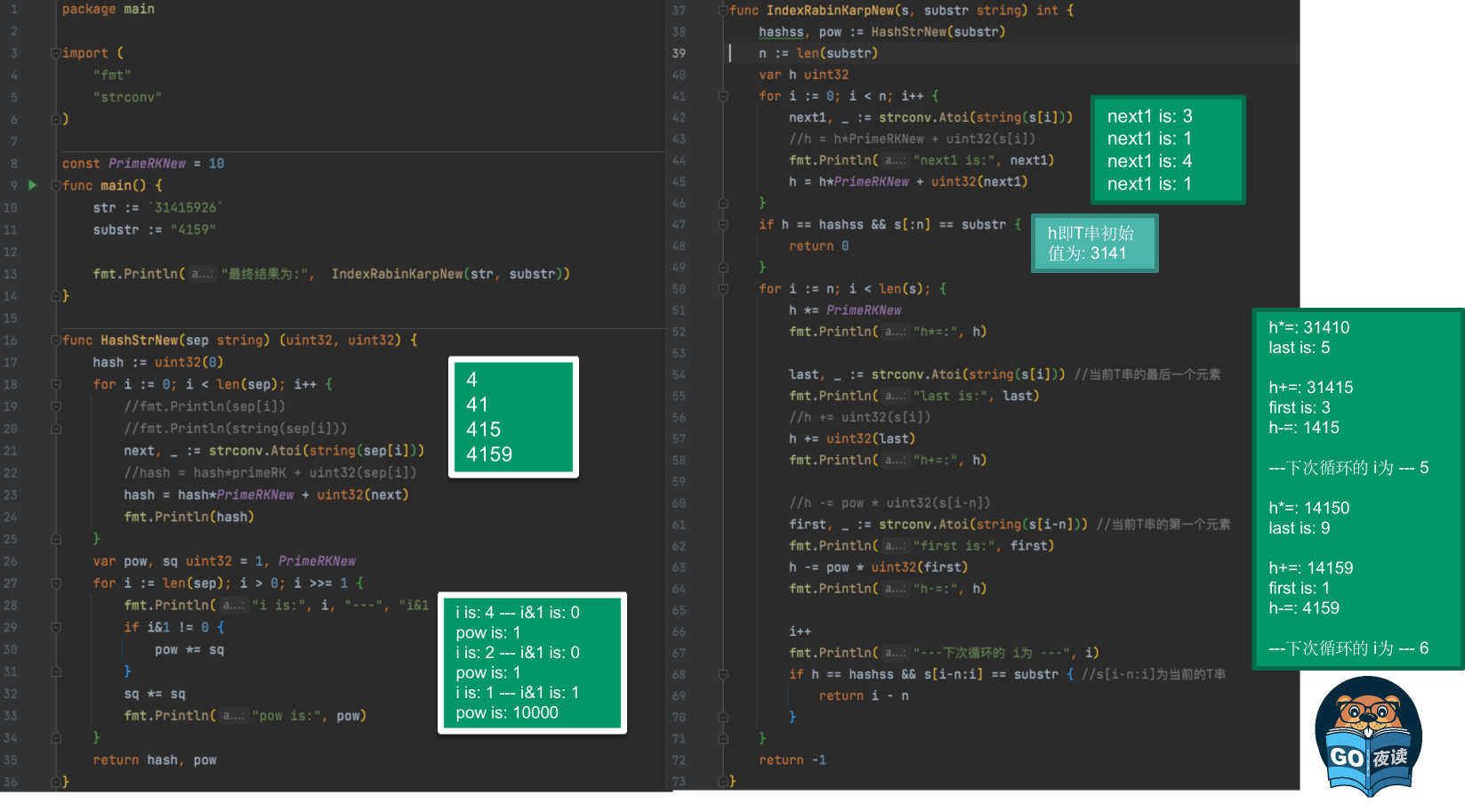
字符串匹配的Rabin–Karp算法
leetcode-28 实现strStr() 更熟悉的字符串匹配算法可能是KMP算法, 但在Golang中,使用的是Rabin–Karp算法 一般中文译作 拉宾-卡普算法,由迈克尔拉宾与理查德卡普于1987年提出 “ 要在一段文本中找出单个模式串的一个匹配,此算法具有线性时间的平均复杂度࿰…...
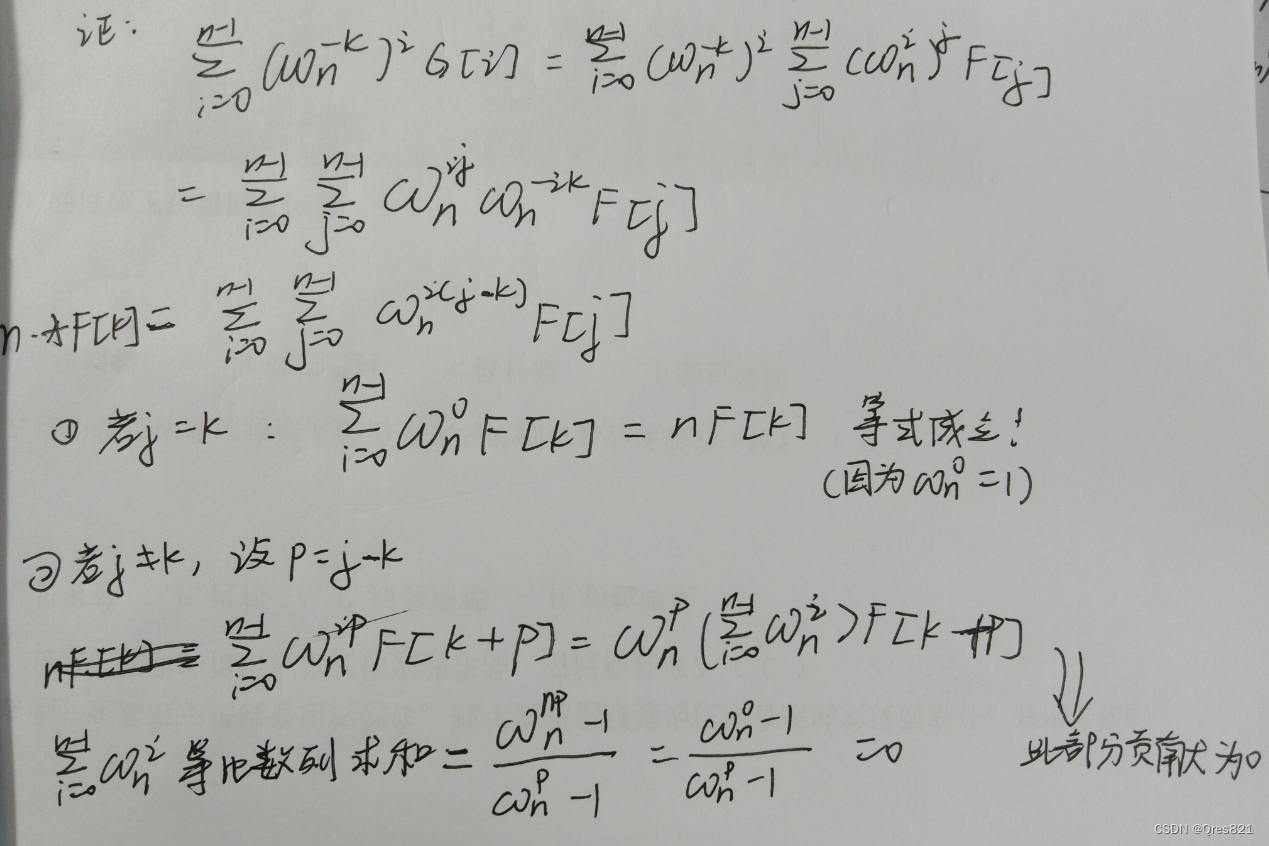
傅里叶变换(FFT)笔记存档
参考博客:https://www.luogu.com.cn/blog/command-block/fft-xue-xi-bi-ji 目录: FFT引入复数相关知识单位根及其相关性质DFT过程(难点)DFT结论(重要)IDFT结论(重要)IDFT结论证明&…...
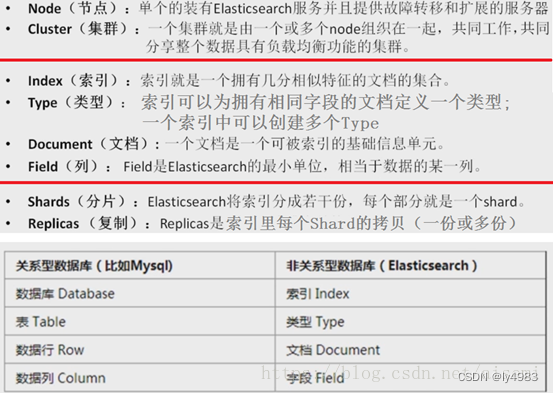
ELK安装、部署、调试 (二) ES的安装部署
ElasticSearch是一个基于Lucene的搜索服务器。它提供了一个分布式多用户能力的全文搜索引擎,基于RESTful web接口操作ES,也可以利用Java API。Elasticsearch是用Java开发的,并作为Apache许可条款下的开放源码发布,是当前流行的企业…...
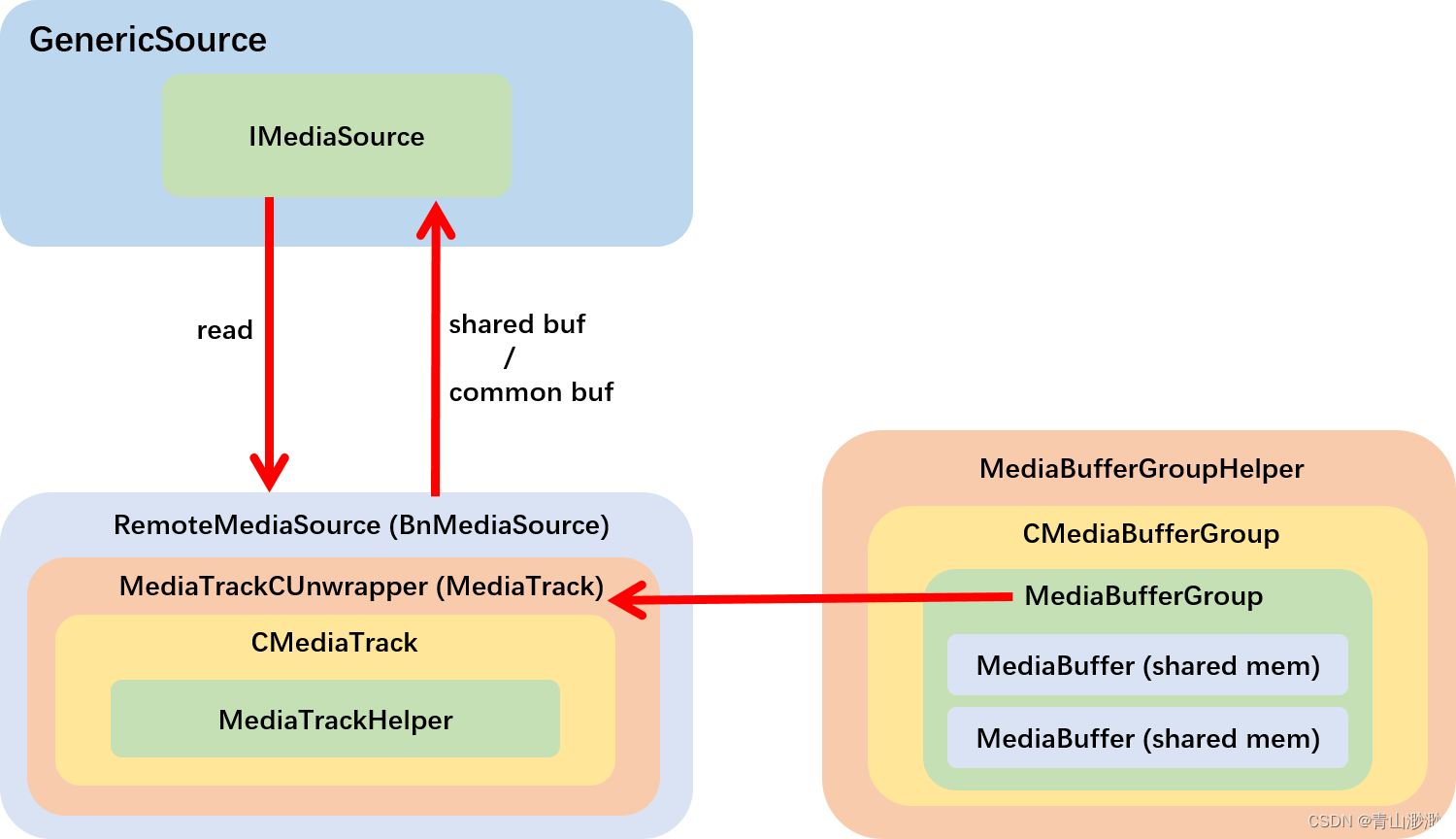
Android 13 - Media框架(8)- MediaExtractor
上一篇我们了解了 GenericSource 需要依赖 IMediaExtractor 完成 demux 工作,这一篇我们就来学习 android media 框架中的第二个服务 media.extractor,看看 IMediaExtractor 是如何创建与工作的。 1、MediaExtractorService media.extractor 和 media.p…...
Flutter 混合开发调试
针对Flutter开发的同学来说,大部分的应用还是Native Flutter的混合开发,所以每次改完Flutter代码,运行整个项目无疑是很费时间的。所以Flutter官方也给我们提供了混合调试的方案【在混合开发模式下进行调试】,这里以Android Stud…...

C语言每日一练------(Day3)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。 今天练习题的关键字: 尼科彻斯定理 等差数列 💓博主csdn个人主页:…...
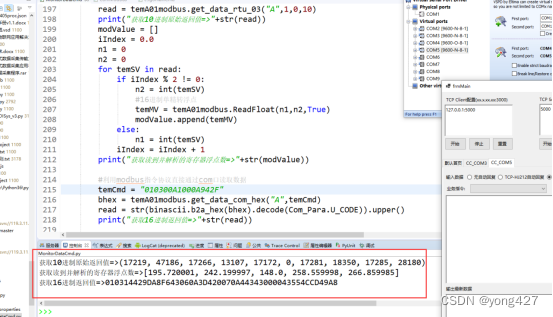
14、监测数据采集物联网应用开发步骤(10)
监测数据采集物联网应用开发步骤(9.2) Modbus rtu协议开发 本章节在《监测数据采集物联网应用开发步骤(7)》基础上实现可参考《...开发步骤(7)》调试工具,本章节代码需要调用modbus_tk组件,阅读本章节前建议baidu熟悉modbus rtu协议内容 组件安装modb…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

