机器学习框架sklearn之特征降维
目录
- 特征降维
- 概念
- 特征选择
- 过滤式
- ①低方差特征过滤
- ②相关系数
- ③主成分分析
特征降维
0维 标量
1维 向量
2维 矩阵
概念
降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程
注:正是因为在进行训练的时候,我们都是使用特征进行学习,如果特征本身存在问题或者特征之间相关性较强,对于算法学习预测会影响较大
降维的两种方式:
- 特征选择
- 主成分分析(可以理解为一种特征提取的方式)
特征选择
①定义
数据中包含冗余或相关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征。
②方法
- Filter(过滤式):主要探究特征本身特点、特征与特征和目标值之间关联
- 方差选择法:低方差特征过滤
- 相关系数
- Embedded(嵌入式):算法自动选择特征(特征与目标值之间的关联)
- 决策树:信息熵、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
③模块
sklearn.feature_selection
过滤式
①低方差特征过滤
-
删除低方差的一些特征
- 特征方差小:某个特征很多样本的值比较相近
- 特征方差大:某个特征很多样本的值都有差别
-
API
sklearn.feature_selection.VarianceThreshold(threshold=0.0)-删除所有低方差特征
-Variance.fit_transform(X)X:numpy array格式的数据[n_samples,n_features]返回值:训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征
- 代码演示
from sklearn.feature_selection import VarianceThreshold
import pandas as pd
def variance_demo():#1.获取数据data=pd.read_csv("data.TXT")print("data:\n", data)#2.实例化一个转换器类transfer=VarianceThreshold(threshold=7)#3.调用fit_transformresult=transfer.fit_transform(data)print("result:\n", result,result.shape)return None
②相关系数
-
皮尔逊相关系数(Pearson Correlation Coefficient)
- 反映变量之间相关关系密切程度的统计指标
-
公式
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2mnqAqBm-1676026457448)(C:\Users\dawei\AppData\Roaming\Typora\typora-user-images\image-20230204224211432.png)]](https://img-blog.csdnimg.cn/376554099339457e956f47113cde805e.png)
-
特点
相关系数的值介于-1与+1之间,即-1<=r<=+1,其性质如下:
- 当r>0时,表示两变量正相关,r<0时,两变量为负相关
- 当|r|=1时,表示两变量为完全相关,当r=0时,表示两变量间无相关关系
- 当0<|r|<1时,表示两变量存在一定程度的相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱
- 一般可按三级划分:|r|<0.4为低度相关;0.4<=|r|<0.7为显著性相关;0.7<=|r|<1为高度线性相关
-
API
from scipy.stats import pearsonr-x:array
-y:array
-Returns:(Pearson`s correlation coefficient,p-value)
- 代码演示
from scipy.stats import pearsonr
def p_demo():# 1.获取数据data = pd.read_csv("data.TXT")print("data:\n", data)# 2.计算两个变量之间的相关系数r=pearsonr(data["one"],data["two"])print("相关系数:\n", r)return None
如果特征与特征之间相关性很高,通过以下方法处理:
①选取其中一个
②加权求和
③主成分分析
③主成分分析
-
定义
高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量
-
作用
是数据维数压缩,尽可能降低原数据维数(复杂度),损失少量信息
-
应用
回归分析或者聚类分析当中
-
API
sklearn.decomposition.PCA(n_components=None)-将数据分解为较低维数空间
-n_components:·小数:表示保留百分之多少的信息·整数:减少到多少特征
-PCA.fit_transform(X)X:numpy array格式的数据[n_samples,n_features]
-返回值:转换后指定维度的array
- 使用
from sklearn.decomposition import PCA
def pca_demo():data=[[2,8,4,5],[6,3,0,8],[5,4,9,1]]#1.实例化一个转换器类transfer=PCA(n_components=2)#2.调用fit_transformresult=transfer.fit_transform(data)print("result:\n",result)return None
相关文章:
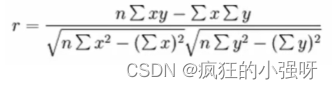
机器学习框架sklearn之特征降维
目录特征降维概念特征选择过滤式①低方差特征过滤②相关系数③主成分分析特征降维 0维 标量 1维 向量 2维 矩阵 概念 降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程 注:正是…...
java实现二叉树(一文带你详细了解二叉树的)
🎇🎇🎇作者: 小鱼不会骑车 🎆🎆🎆专栏: 《数据结构》 🎓🎓🎓个人简介: 一名专科大一在读的小比特,努力学习编程是我唯一…...
学弟学妹少走弯路,超完整算法刷题路线出炉
大家好,我是帅地。 本篇文章主要讲解下面三个事: 1、自己学习算法的一些经历 2、大家学习算法存在的一些普遍问题 3、给大家规划的算法刷题路线 一、算法学习往事 记得当初学了 C 语言就开始刷题了,刷题倒不是面试,而是为了…...
Windows截取gif动态图的软件 ScreenToGif 的安装、使用教程
一、概述 👉GIF(Graphics Interchange Format),又称图形交换格式,是一种公用的图像文件格式标准,于1987年由Compu Serve公司成功研发并推出。 👉GIF用于以超文本标志语言方式显示索引彩色图像&a…...

C++程序设计——多态:虚函数、抽象类、虚函数表
注:以下示例均是在VS2019环境下 一、多态的概念 通俗来讲,多态就是多种形态,当不同的对象去完成某个行为时,会产生出不同的状态。即不同继承关系的类对象,去调用同一函数时,产生不同的行为。 比如”叫“这…...
OpenMMLab AI实战营 第6课 语义分割与MMSegmentation
第6课 语义分割与MMSegmentation 1. 语义分割简介 任务:将图像按照物体的类别分割成不同的区域,等价于对每个像素进行分类应用 无人驾驶人像分割智能遥感医疗影像分析 语义分割 vs 实例分割 vs 全景分割 语义分割:仅考虑像素的类别…...

产业互联网是对互联网的衍生和进化,也是一次重塑和再造
互联网并不仅仅只是充当撮合和中介的角色,它应当具备更多的功能和意义。只有这样,它的发展才能够真正全面和完善。产业互联网的衍生和出现,正是在互联网进化的基础之上出现的。这是我们看到之所以会有那么多的互联网玩家投身到产业互联网的浪…...
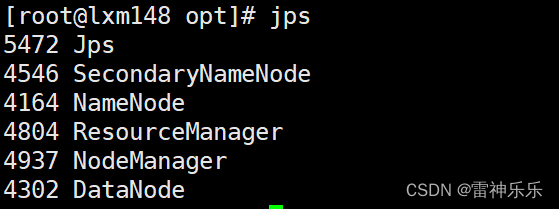
Shell脚本之——Hadoop3单机版安装
目录 1.解压 2.文件重命名 3.配置环境变量 4.hadoop-env.sh 5.core-site.xml 6. hdfs-site.xml 7. mapred-site.xml 8.yarn-site.xml 9.完整脚本代码(注意修改主机名) 10.重启环境变量 11.初始化 12.启动服务 13.jps查询节点 1.解压 tar -zxf /opt/install/hadoo…...
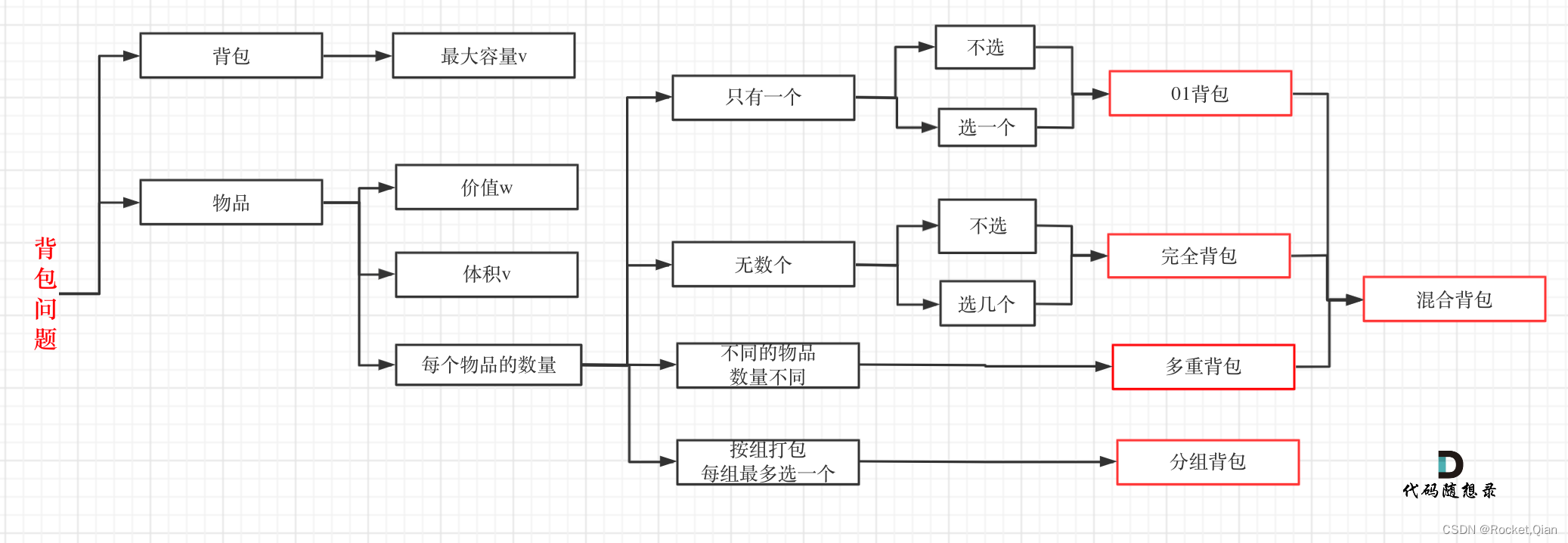
代码随想录NO39 |0-1背包问题理论基础 416.分割等和子集
0-1背包问题理论基础 分割等和子集1. 0-1背包问题理论基础(二维数组实现)2. 0-1背包问题理论基础 二(一维数组实现)1. 0-1背包问题理论基础(二维数组实现) 背包问题一般分为这几种: 0-1背包问题:有n件物品和一个最多能背重量为w…...
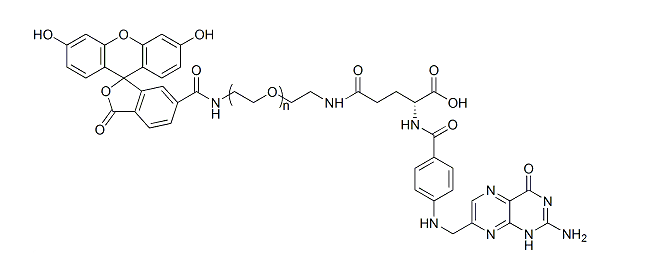
FITC-PEG-FA,荧光素-聚乙二醇-叶酸,FA-PEG-FITC,实验室科研试剂,提供质量检测
FITC-PEG-FA,荧光素-聚乙二醇-叶酸 中文名称:荧光素-聚乙二醇-叶酸 英文名称:FITC-PEG-FA 英文别名:Fluorescein-PEG-Folic Acid 性状:基于不同的分子量,呈白色/类白色固体,或粘稠液体。 溶…...

简洁易懂:源码+实战讲解Redisson并发锁及看门狗自动续期
1 缘起 有一次同事问Redisson存储的键是否为hash? 我当时,没有看Redisson的相关源码,只知道应用, 所以没有办法回答,于是开始看看Redisson实现的源码, 顺便写了一个单机Redisson测试, 发现Redi…...
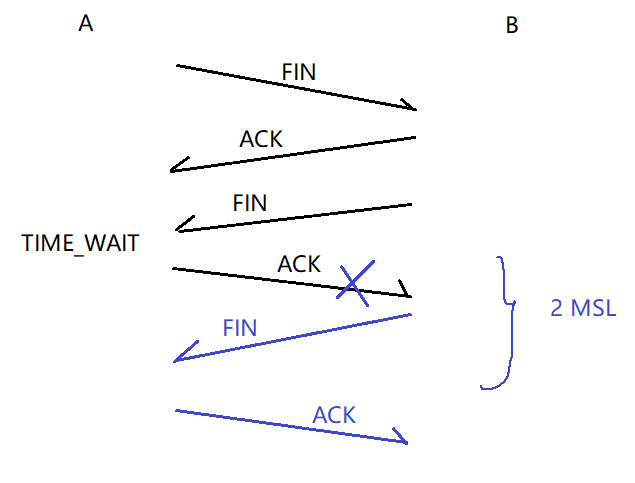
TCP 三次握手和四次挥手
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录TCP 建立连接(三次握手)为啥不能是 4 次?为啥不能是 2 次?三次握手的意义:TCP 断开连接(四…...
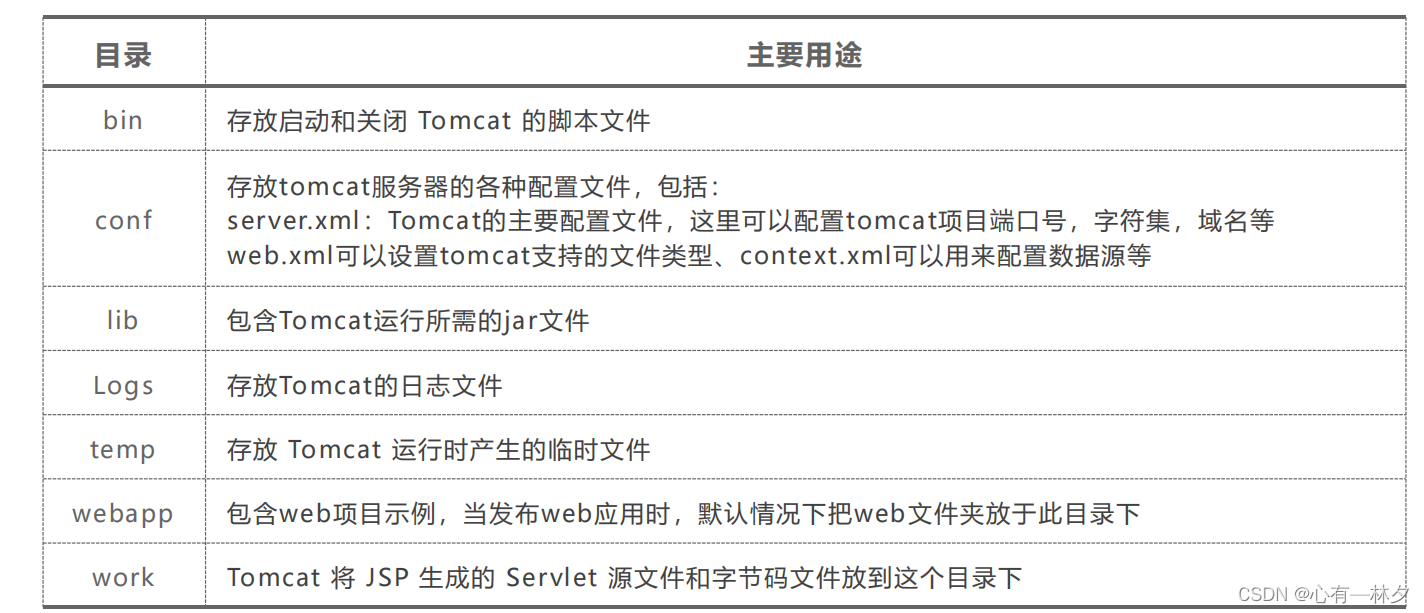
JavaWeb复习
JavaWeb复习一.概述1.概念2.B/S和C/S 架构二.HTTP通信协议概述1.概念2.HTTP1.0 与 HTTP1.1 版本3.HTTP 协议组成4.常见状态码5.GET 与 POST 请求方式三.Tomcat1.Web服务器介绍2.安装(Windows)3.Tomcat目录结构4.server.xml部分配置解释四.Servlet1.概念2…...

P14 PyTorch AutoGrad
前言:激活函数与loss的梯度PyTorch 提供了Auto Grad 功能,这里系统讲解一下torch.autograd.grad系统的工作原理,了解graph 结构目录:1: require_grad False2: require_grad True3: 多层bakcward 原理4: in…...

前端报表如何实现无预览打印解决方案或静默打印
在前端开发中,除了将数据呈现后,我们往往需要为用户提供,打印,导出等能力,导出是为了存档或是二次分析,而打印则因为很多单据需要打印出来作为主要的单据来进行下一环节的票据支撑, 而前端打印可…...

Operating System Course 2 - My OS
Computer Startup process上一篇:http://t.csdn.cn/XfUKt 讲到这个启动设备的第一个扇区:引导扇区。那么引导扇区的代码长什么样子?这里得看引导扇区代码源文件bootsect.s(.s后缀文件为用汇编语言编写的源代码文件)。另…...

离散数学 课时一 命题逻辑的基本概念
1 命题 1、命题:可以判断其真值的陈述句 2、真值:真或者假(1或者0) 3、真命题:真值为真的命题 4、假命题:真值为假的命题 5、原子命题:不可以再被分解成更简单的命题 6、复合命题:由原子命题通过联结词联结…...
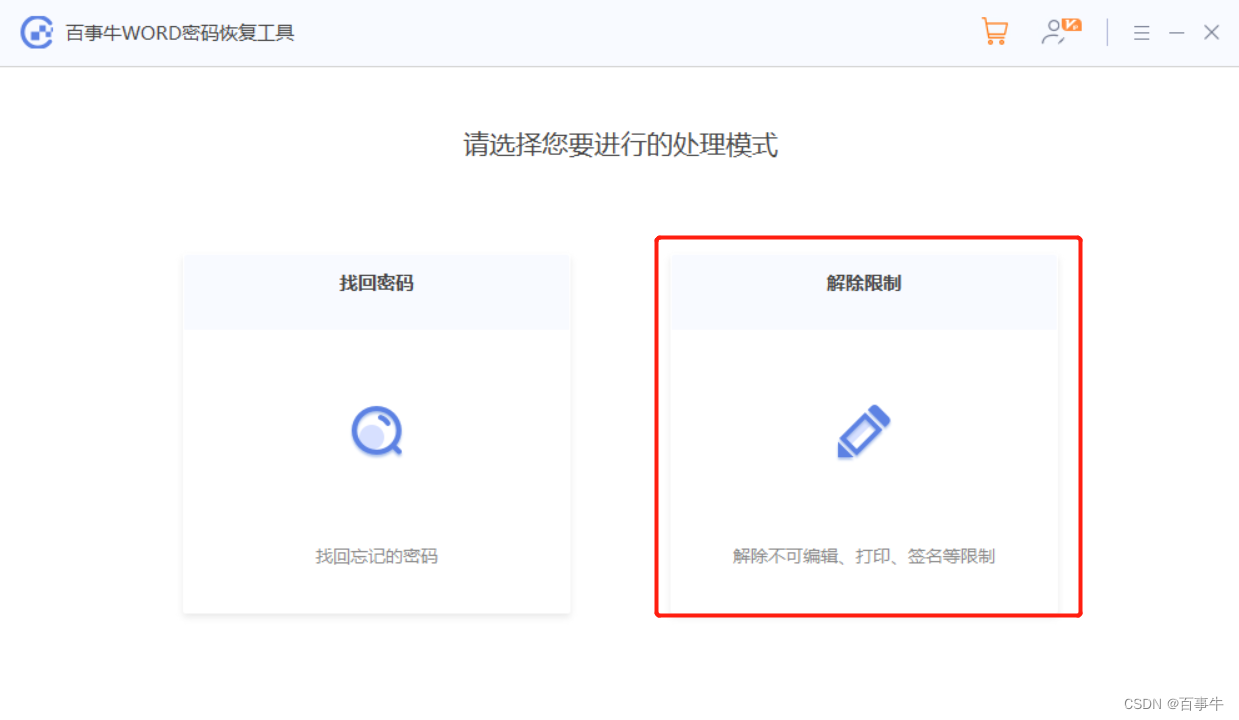
Word文档带有权限密码怎么办?
Word文档的权限密码指的是什么?其实这是Word文档的保护方法之一,具体指Word文档的编辑、修改受到了限制,需要输入密码才能进行。 设置了权限密码的Word文档还是可以直接打开,只有当需要编辑或者修改内容的时候,才会发…...
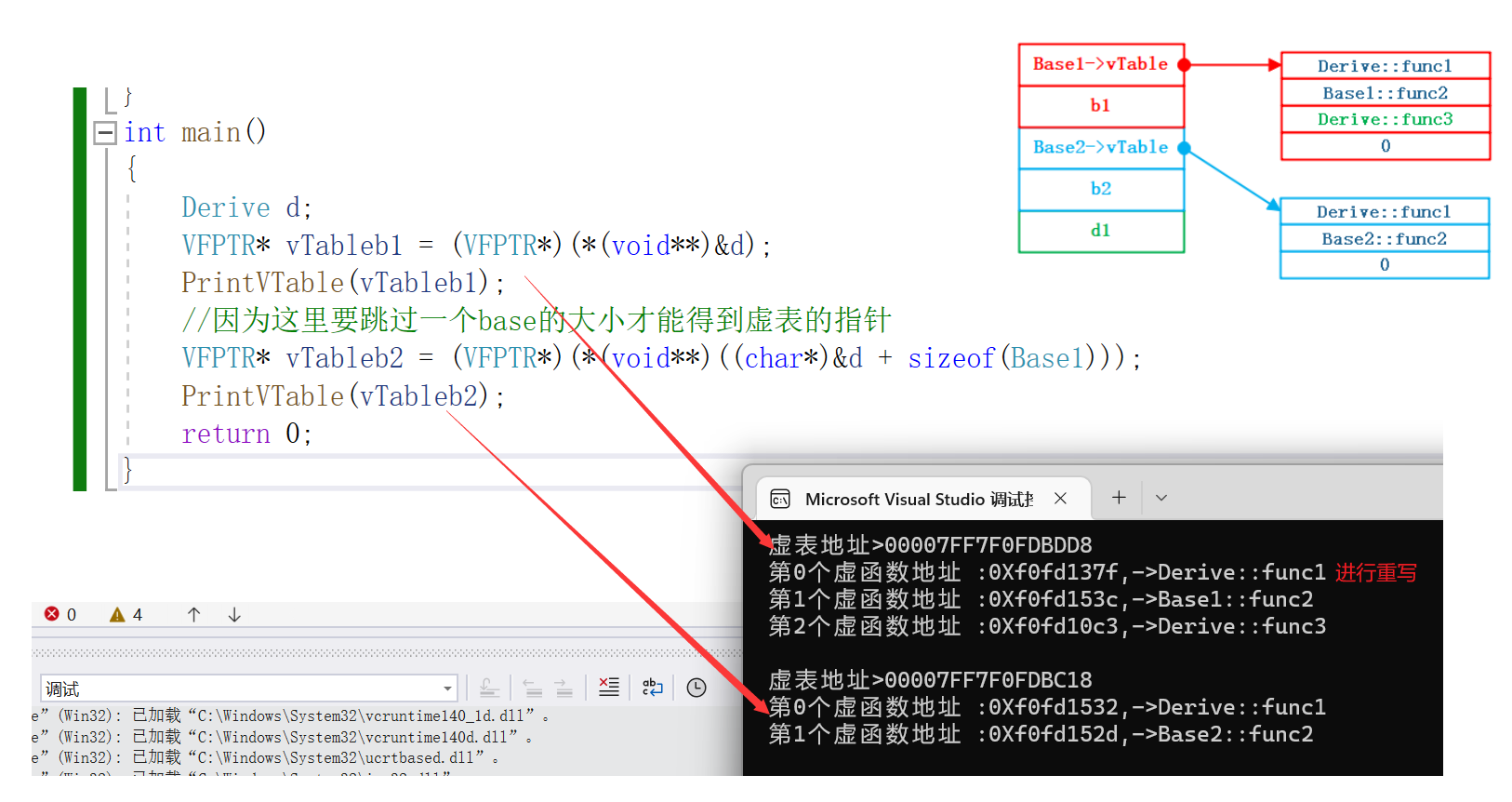
C++多态
1. 多态的概念1.1 概念多态的概念:通俗来说,就是多种形态,具体点就是去完成某个行为,当不同的对象去完成时会产生出不同的状态举个例子:比如买票这个行为,当普通人买票时,是全价买票;…...

访问学者如何申请美国J1签证?
一、申请美国J1签证的步骤: 第一步:填写I901表。 填写I901表会收取SERVIS费用180美元,可以用VISA/Master卡直接网上支付。填完后打印收据单或者存成PDF后续再打印,记下I901收据编号。 第二步:DS-160表填写。 填写DS-…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
