day-36 代码随想录算法训练营(19)part05
435.无重叠区间
思路:首先对数组排序,只需要关注重叠区间就行,有重叠时计数+1,然后更新当前右边界为重叠区间中的最小右边界。
763.划分字母区间
思路:记录每一个字母的最远位置,然后从头开始遍历,不断更新最远位置,当i等于最远位置时,说明这个区间内的字母在后面不会再出现;此时最远距离-起始位就是区间长度,然后更新起始位到下一位。
56.合并区间
思路:先对区间进行排序,临时空间保存第一个区间。然后判断是否重叠,存在重叠时更新临时空间最大右边界;不存在重叠时,把临时区间添加进结果,然后对临时空间清空,再保存当前区间,作为下一次判断的起始区间。
746.使用最小花费爬楼梯
思路:每一可以爬一个楼梯或者两个楼梯,就在两种情况中找最小值
注意:每一个位置的花费当往上爬才累加
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();int dp[n+1];dp[1]=dp[0]=0;//第一步是不需要花费的for(int i=2;i<=n;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);//每一个位置的花费都加上了}return dp[n];}
};62.不同路径
思路:
-
1.首先确定dp存储的是,到达第 i 个位置的所有路径数
-
2.初始化,第一行和第一列的每个位置都只有一条路径到达
-
3.递推式 dp[i][j]+=dp[i][j-1]+dp[i-1][j] (累加是因为每到一个位置,路径的数量都在递增)
-
4.遍历顺序:直接从前往后遍历
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>>dp(m,vector<int>(n,0));for(int i=0;i<n;i++)//第一行每个位置都只有一种走法dp[0][i]=1;for(int i=0;i<m;i++)//第一列每个位置都只有一种走法dp[i][0]=1;for(int i=1;i<m;i++){for(int j=1;j<n;j++){dp[i][j]+=dp[i][j-1]+dp[i-1][j];//每个位置只有从左边来和上边来}}return dp[m-1][n-1];}
};相关文章:
part05)
day-36 代码随想录算法训练营(19)part05
435.无重叠区间 思路:首先对数组排序,只需要关注重叠区间就行,有重叠时计数1,然后更新当前右边界为重叠区间中的最小右边界。 763.划分字母区间 思路:记录每一个字母的最远位置,然后从头开始遍历…...

Vue3 实现JS动态改变CSS样式
以颜色为例子 定义颜色变量 import { reactive } from vue; // 可变的主题颜色 let chooseColor reactive({--color: #be2a27 }) CSS中使用 var() 函数引用颜色变量(这里是用elementPlus为例, 也可以改) :deep(.is-active) {color: var(--color);border-bottom: 2px solid…...
最新社区团购电商小程序源码 无bug完美运营版+详细搭建部署教程
分享一个开源社区团购电商小程序源码,无bug完美运营版,含完整前后端详细搭建部署教程。 系统运营模式:整合线下社区资源,由各快递代收点、社区便利店、社区物业、业主等发起的社区微信群,推送商品信息,消费…...
恒运资本:三大指数震荡走低,地产股大幅回撤,光刻胶概念逆市上涨
周四(8月31日),到上午收盘,A股三大指数震动走低。其间,上证指数跌0.53%,报3120.39点;深证成指和创业板指别离跌0.55%、0.54%;沪深两市算计成交额5290.51亿元,总体来看&am…...

DP读书:不知道干什么就和我一起读书吧——以《鲲鹏处理器 架构与编程》中鲲鹏软件的构成为例
DP读书:不知道干什么就和我一起读书吧 为啥写博客:好处一:记录自己的学习过程优点二:让自己在各大社群里不那么尴尬推荐三:坚持下去,找到一个能支持自己的伙伴模版:鲲鹏软件构成硬件特定软件1. …...

现货黄金走势图中的止盈点
对平仓时机的把握能力,是衡量现货黄金投资者水平的重要标志,止盈点设置得是否合理,在行情兑现的时候能否及时地离场,是事关投资者账户浮盈最终能否落袋为安的“头等大事”,要在现货黄金走势图中把握止盈点,…...
MyBatisPlus实现多租户功能
前言:多租户是一种软件架构技术,在多用户的环境下,共有同一套系统,并且要注意数据之间的隔离性。 一、SaaS多租户简介 1.1、SaaS多租户 SaaS,是Software-as-a-Service的缩写名称,意思为软件即服务&#x…...

JAVA-斐波那契数列
输入一个整数 n ,求斐波那契数列的第 n 项。 假定从 0 开始,第 0 项为 0 。 数据范围 0≤n≤39 样例 输入整数 n5 返回 5class Solution {public int Fibonacci(int n) {int[] dpnew int[250];dp[0]0;dp[1]1;for(int i2;i<n;i){dp[i]dp[i-1]dp[i-2];}…...

keepalived+lvs(DR)
目录 一,作用 二,调度器配置 1,安装keepalived 2, 安装ipvsadm 3, 配置keepalived 4. 查看lvs节点状态 5, web节点配置 1.1 调整ARP参数 1.2 配置虚拟IP地址 1.3添加回环路由 1.4安装nginx并写…...
基于Matlab实现频谱分析(附上源码+数据集)
Matlab是一个功能强大的数值计算和科学计算软件,可以用于频谱分析。频谱分析是一种信号处理技术,用于将时域信号转换为频域信号,以便更好地理解信号的频率特性。本文将介绍使用Matlab实现频谱分析的方法。 文章目录 部分源码完整源码数据集下…...
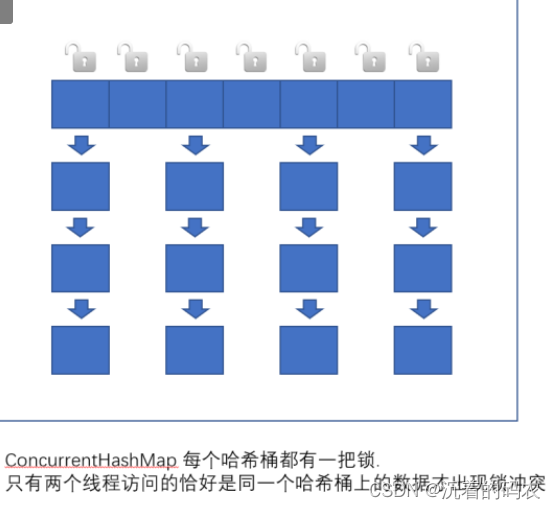
【Java】多线程(进阶)
多线程进阶 常见的所策略乐观锁和悲观锁重量级锁和轻量级锁自旋锁和挂起等待锁自旋锁挂起等待锁 读写锁和互斥锁读写锁互斥锁 公平锁和非公平锁公平锁非公平锁 可重入锁和不可重入锁可重入锁不可重入锁 CASCAS应用实现原子类实现自旋锁 CAS的ABA问题 synchronized原理基本特点加…...
BMP图片读写实践:rgb转bgr
本实理论上支持24位图和32位图,实际上只测试了24位。原理很简单,就是RGB中的蓝色字节和红色字节交换。 测试代码1: #include <stdio.h> #include <unistd.h> #include <sys/stat.h> #include <stdlib.h> #include &l…...

交通科技与管理杂志社交通科技与管理编辑部2023年第9期目录
专家论坛 黑龙江省经济高质量发展与生态环境保护耦合协调发展研究 刘降斌;祃玉帅; 1-5142 我国省际数字经济高质量发展水平综合评价研究 耿娟;毕晨曦; 6-8 振兴龙江《交通科技与管理》投稿邮箱:cn7kantougao163.com(注明投稿“《交通科技与管理》”) 数…...

根据源码,模拟实现 RabbitMQ - 网络通讯设计,实现客户端Connection、Channel(完结)
目录 一、客户端代码实现 1.1、需求分析 1.2、具体实现 1)实现 ConnectionFactory 2)实现 Connection 3)实现 Channel 二、编写 Demo 2.1、实例 2.1、实例演示 一、客户端代码实现 1.1、需求分析 RabbitMQ 的客户端设定ÿ…...

The Cube++ Illumination Estimation Dataset 文章总结
The Cube++ Illumination Estimation Dataset 颜色恒常性数据集Cube++ Type: Academic Journal Author: Ershov Link: https://ieeexplore.ieee.org/document/9296220 Select: ⭐️⭐️⭐️⭐️ Status: Done 备注: Cube++数据集 Journal: ACCESS Year: 2020 code: https://g…...

“烧钱”的大模型,如何迈过存储这道坎?
几乎每一个行业都在讨论大模型,每一个行业巨头都在训练大模型,人工智能已然进入了大模型主导的时代。 想要占领大模型应用的高地,数据和算力可以说是不可或缺的基石。和算力相关的讨论已经有很多,以至于英伟达的市值在2023年翻了…...
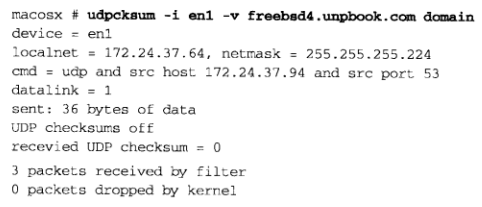
UNIX网络编程卷一 学习笔记 第二十九章 数据链路访问
目前大多操作系统都为程序提供访问数据链路层的功能,此功能可提供以下能力: 1.能监视由数据链路层接收的分组,使得tcpdump之类的程序能运行,而无需专门的硬件设备来监视分组。如果结合使用网络接口进入混杂模式(promis…...
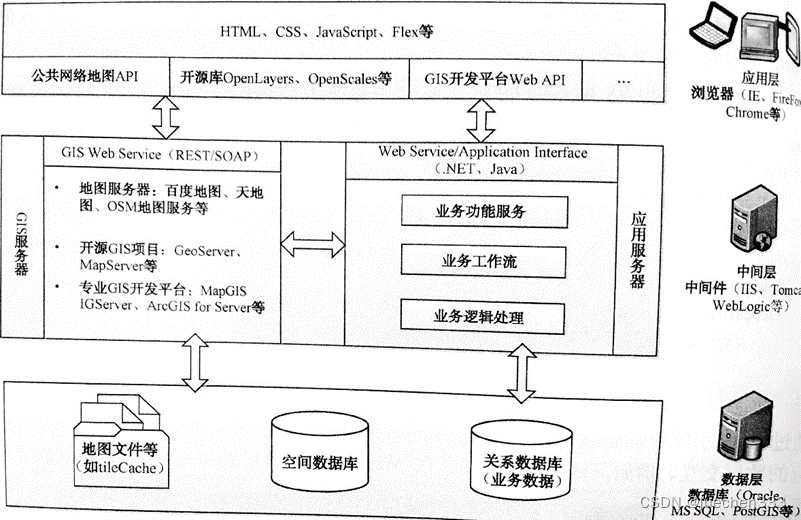
WebGIS的一些学习笔记
一、简述计算机网络的Internet 概念、网络类型分类、基本特征和功用是什么 计算机网络的Internet 概念 计算机网络是地理上分散的多台独立自主的计算机遵循约定的通讯协议,通过软、硬件互连以实现交互通信、资源共享、信息交换、协同工作以及在线处理等功能的系统…...
java Spring Boot将不同配置拆分入不同文件管理
关于java多环境开发 最后还有一个小点 我们一般会将不同的配置 放在不同的配置文件中 好处肯定就在于 想换的时候非常方便 那么 我们直接看代码 我们将项目中的 application.yml 更改代码如下 spring:profiles:active: dev这里 意思是 我们选择了dev 环境 然后创建一个文件 …...

Docker(三) 创建Docker镜像
一、在Docker中拉取最基本的Ubuntu系统镜像 搜索Ubuntu镜像 Explore Dockers Container Image Repository | Docker Hub 下载镜像 docker pull ubuntu:22.04 二、在镜像中添加自己的内容 使用ubuntu镜像创建容器 docker run -it ubuntu:20.04 /bin/bash 在容器中创建了一个文…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
