【一等奖方案】大规模金融图数据中异常风险行为模式挖掘赛题「NUFE」解题思路
第十届CCF大数据与计算智能大赛(2022 CCF BDCI)已圆满结束,大赛官方竞赛平台DataFountain(简称DF平台)正在陆续释出各赛题获奖队伍的方案思路,欢迎广大数据科学家交流讨论。
本方案为【大规模金融图数据中异常风险行为模式挖掘】赛题的一等奖获奖方案,赛题地址:https://www.datafountain.cn/competitions/586(戳底部“阅读原文”可直达)

获奖团队简介
团队名称:NUFE
团队成员:队长韩鲁峰,就职于南京财经大学,高级工程师。队员张斌,就职于南京财经大学,工程师。
团队荣誉:2018年华为软件精英挑战赛季军、2020年CCF BDCI 基于买方意向的货物撮合交易二等奖、2019华为云鲲鹏开发者大赛决赛第二名、2021 CCF BDCI大规模金融仿真图数据中金融交易环路查询的设计与性能优化二等奖。
所获奖项:一等奖
摘 要
图计算在金融场景的运用最为成熟,贷前审批、贷后管理、反欺诈、反洗钱等业务均对图计算能力有要求,包含但不限于k度邻居、找环、社区发现。业界常用的频繁子图挖掘算法可以帮助发现高频出现的子图结构,如何使用频繁子图挖掘算法高效地进行异常风险行为模式挖掘显得尤为重要。
本赛题要求在尽可能短的时间内挖掘出不小于频繁度(f >= 10000)的频繁子图模式集合。子图同构是NP难问题。虽然可以使用图的编码来代替同构计算,但是此类方法的复杂度也相当高,另外还存在历史结果的使用问题。
针对题目要求本文主要做了以下几个方面的工作:
-
在题目要求下输出准确的频繁模式以及模式对应的频繁度。
-
多次压缩编码数组的长度,可以遍历数据集一次求出就将所有的候选模式的频繁度求出。
-
重新构图,减少图结构大小,增加缓存命中率。
-
通过实验验证此方法的高效性,准确性。
关 键 词
子图同构,频繁模式,NP难问题
1 背景及算法介绍
1.1 背景介绍
频繁子图挖掘的两个难点是支持度的计算和候选子图的生成,支持度计算中的子图同构是NP 难题,虽然可以使用图的编码来代替同构测试但是此类方法的复杂度也相当高,另外还存在历史结果的使用问题。如果使用历史同构图的信息可以加快测试的速度,但是会极大增加存储量,反之不使用,在同构测试方面又会做大量的重复工作;候选子图生成如果没有高效的剪枝算法会产生大量的冗余结果,对存储和支持度的计算都是一个极大的考验。单一大图频繁子图挖掘当前已经多种算法,主要包括非精确挖掘算法(SUBDUE,SEus)、不相交子图挖掘算法(Grew,SiGram)、分布式挖掘算法(MRPF,MRSUB)和CSP 搜索挖掘算法(GRAMI[3])等。2014年提出的GRAMI算法将难点转为限制约束问题,该算法在单机频繁子图挖掘中效较好。本文简化的编码方式,先通过图拓展算出3阶候选模式,然后计算候选模式的MNI支持度作为最终模式的支持度。
1.2 算法介绍
赛题使用简化的金融仿真数据,数据为带有时间戳和金额的账户间交易、转账等数据。基于此数据自动挖掘出不小于频繁度(f >= 10000)的频繁子图模式集合。本次给到的图是属性图结构,判定子图同构的方法需要属性值匹配,严格匹配属性包括:名称、金额、策略名和业务编码。本文算法流程图如图1,各个步骤的细节将在下一章详细介绍。

图1
2 本方案流程
2.1 读取数据及优化
点数据和边数据如下所示,点数据中有效字段为id和name,边数据中有效字段为id,金额,策略名和业务编码。数据分析后发现,点数据中name只有三种类型Jobs、Mike和John,需要将name映射成{0,1,2}的数字方便编码,此处我们计算name每个字节的ASCII和,映射到固定数字上,而不需要用Hash表。边数据中策略名和业务编码只有最后一个字符不一样,所以解析这两个字段时只用解析最后一个字符,这样既可以方便后续的编码,又可以节省解析时间。
点数据:
799999,Jobs,1587334106293,0
799998,John,1585916964769,0
799997,Jobs,1587852713474,0
799996,Jobs,1585425941502,0
799995,Mike,1586242334882,0
799994,Jobs,1584384932575,0
边数据:
684821,434860,1590492254126,5.0,strategy_name-4,1590492251120278,buscode3,,,,,,
684821,434860,1591061355388,0.0,strategy_name-4,159106135809535,buscode3,,,,,,
684821,434860,1590945232703,33.0,strategy_name-4,159094523696782,buscode3,,,,,,
349837,98007,1587894603848,2.0,strategy_name-4,158789460447921,buscode1,,,,,,
181713,317857,1588705807550,40.0,strategy_name-4,158870580500216,buscode2,,,,,,
181713,317857,1588326392299,10.0,strategy_name-4,158832639552221,buscode2,,,,,,
104178,101658,1589394253501,11.0,strategy_name-6,158939425206018,buscode1,,,,,,
我们将代码优化前进行了对比测试,如下图2。可发现优化后无论是单线程还是多线程的读取速度都得到显著提升。
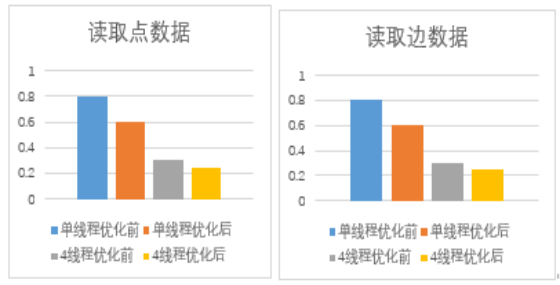
图2
2.2 图剪枝及重构
Grami在解决单一大图频繁子图挖掘性能表现优异,它采用CSP计算子图同构来代替存储实例。并且根据问题的定义,在计算支持度时,并不计算子图的精确的支持度,而是只证明子图的支持度大于阈值就停止。本文采用类似的方法,在计算一阶子图频繁度时并不精确算出频繁度,只计算其频繁度的最大值,将不满足阈值的边全部删掉,保证频繁模式都在剩下边拓展图中即可。为了提高CPU缓存的命中率,我们对剩下的边重新构图,去掉不可能存在满足条件的3阶子图的边,此外我们把每条边数据都存在uint64_t中,提高缓存加载条数。虽然图重构增加了此部分的时间开销,但在后续三阶子图查找过程中节省了很多的时间,整体上程序运行速度得到了提高。
#define MERGE(a,b,c,d) ((uint64_t)(uint64_t(a) << 32u|uint64_t(b)<<16u|uint64_t(c)<<8u| uint64_t(d)))
#define AIM(a) (uint32_t(a >> 32u))
#define AMT(a) (uint16_t(a>>16u))
#define STRATEGY(a) (uint8_t(a>>8u))
#define BUSCODE(a) (uint8_t(a))
单条边的编码我们采用进制编码的形式,具体实现过程如下:
radix=max_amt*max_buscode*max_strategy*max_name*max_name;
radix_=max_amt*max_buscode*max_strategy*max_name;
radix__=max_amt*max_buscode*max_strategy;
radix___=max_buscode*max_strategy;
radix____=max_buscode;
uint32_tcode=0;
code+=radix_*account_ids[src_id];
code+=radix__*account_ids[aim_ids[edge_id]];
code+=radix___*amts[edge_id];
code+=radix____*strategy_names[edge_id];
code+=buscodes[edge_id];
2.3 确定候选模式
一阶子图使用DFS向后拓展,拓展过程不精确计算频繁模式的支持度。虽然会存在不满足MNI支持度的子图,但时可以确保正确答案的频繁模式集合是候选模式集合的子集。3阶子图不能直接使用上面的进制编码,需要将一阶的进制编码重新编码,一阶编码中存在大量小于阈值的编码,所以可以将满足阈值的编码重新编码到成新整数,减小最大编码的值,使三阶子图也可以使用上述编码方法,只是每条边都需要二次编码。具体过程如下图3,其中阈值为10000,对于小于阈值的边,不需要二次编码。
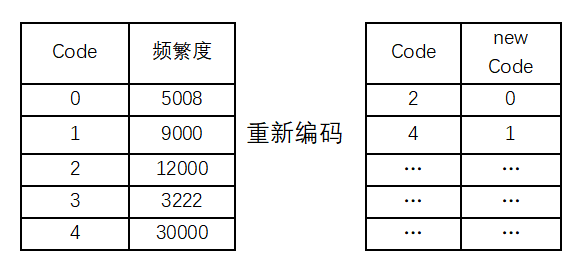
图3
2.4 计算频繁度
通过上述方法求出候选模式后,分别求出每个模式的频繁度。正常情况下如果有n种候选模式,需要搜索n次图,由于本题中候选模式较少,可以通过二维数组遍历一次图求出所有模式的频繁度。这里需要将三阶子图编码进行再次编码。减小二维数组的规模,编码方式参考图3,去掉不满足条件的模式编码。在计算频繁度时,采用MNI(minimum image based suppor)支持度,就是找到节点映射数量的最小值。具体过程如图4,图中MNI值为3。
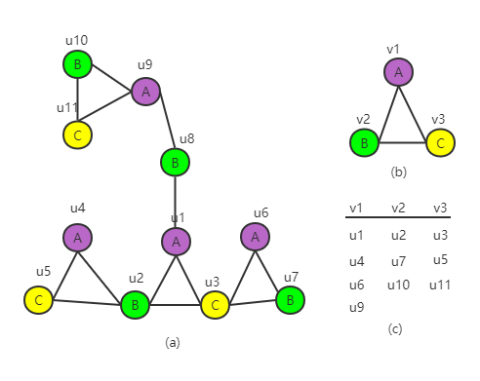
图4
2.5 充分利用并行运算
在程序的各个阶段,都尽量使用并行运算,我们使用OpenMP并行库支持程序的任意线程的并行化,该并行库编降低的并行编程的难度,让我们把时间都投入到优化算法本身,而并非并发编程。
3 实验结果与分析
本题数据集有四个文件,2个点文件2个边文件:
account:顶点数:800000
card:顶点数:600000
account_to_card:边数:3410191
account_to_account:边数:6010512
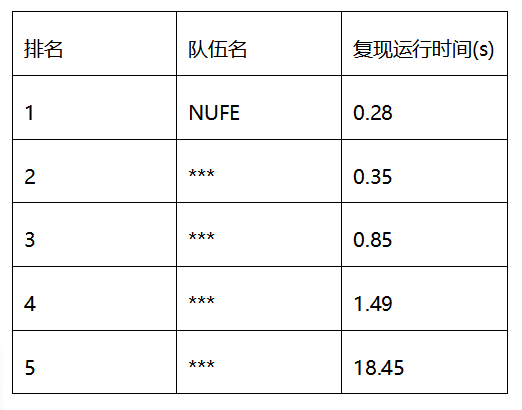
表1:执行时间
通过表1可以看出本方案执行时间比第二名优化了20%,证明本文的优化方案效果更加明显。
致谢
这次比赛让我们深入了解了性能优化相关算法,通过阅读大量的前沿论文,以及自我思考,不断突破自己的极限分数。感谢主办方提供这样的平台,让我们有幸参与其中,与其他选手共同比拼进步。感谢出题方出了一道这么有趣的题目,从实际业务需求抽象成赛题。感谢工作人员的辛苦答疑,让我们在比赛中更轻松更快速的解决问题。希望CCF BDCI越办越好。
参考
[1] Wang Wei Zhou Haofeng, Yuan Qingqing, etc., frequent pattern mining based on graph theory[J]. Journal of computer research and development, 2005, and (2) : 230-235.王伟,周浩峰,袁青青,等。基于图论的明频繁模式[J]。计算机研究与发展,2005,42(2):230-235。
[2] 李先通,李建中,高宏.一种高效频繁子图挖掘算法[J].软件学报,2007,18(10):2469-2480.LI Xiantong, LI Jianzhong, GAO Hong. AN efficient frequent subgraph mining algorithm [J]. Journal of Software,2007, 18(10) : 2469-2480.
[3] Bhuiyan M A, Hasan M A. An Iterative MapReduce Based Frequent Subgraph Mining Algorithm [J]. Knowledge & Data Engineering IEEE Transactions on, 2015, 27(3):608-620.
我是行业领先的大数据竞赛平台 @DataFountain ,欢迎广大政企校军单位合作办赛,推动优秀数据人才揭榜挂帅!
相关文章:

【一等奖方案】大规模金融图数据中异常风险行为模式挖掘赛题「NUFE」解题思路
第十届CCF大数据与计算智能大赛(2022 CCF BDCI)已圆满结束,大赛官方竞赛平台DataFountain(简称DF平台)正在陆续释出各赛题获奖队伍的方案思路,欢迎广大数据科学家交流讨论。 本方案为【大规模金融图数据中…...

npm install 报错
npm install 报错 npm install 报错 npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: yudao-ui-admin1.8.0-snapshot npm ERR! Found: eslint7.15.0 npm ERR! node_modules/eslint npm ERR! dev eslint&q…...

专业人士使用的3个好用的ChatGPT提示
AI正在席卷世界。从自动化各个领域的任务到几秒钟内协助我们的日常生活,它有着了公众还未理解的巨大价值……除非你是专业人士。 专业人士一般都使用什么提示以及如何使用的?这里是经验丰富的懂ChatGPT的专业人士才知道的3个提示。好用请复制收藏。 为…...

doris系列2: doris分析英国房产数据集
1.准备数据 2.doris建表 CREATE TABLE `uk_price_paid` (`id` varchar(50) NOT NULL,`price` int(20),`date` date...

精准运营,智能决策!解锁天翼物联水利水务感知云
面向智慧水利/水务数字化转型需求,天翼物联基于感知云平台创新能力,提供涵盖水利水务泛协议接入、感知云水利/水务平台、水利/水务感知数据治理、数据看板在内的水利水务感知云服务,构建水利水务感知神经系统新型数字化底座,实现智…...

CleanMyMac最新版4.14Mac清理软件下载安装使用教程
苹果电脑是很多人喜欢使用的一种电脑,它有着优美的外观,流畅的操作系统,丰富的应用程序和高效的性能。但是,随着时间的推移,苹果电脑也会产生一些不必要的文件和数据,这些文件和数据就是我们常说的垃圾。那…...

String.Format方法详解
在Java中,String.format() 方法可以用于将格式化的字符串写入输出字符串中。该方法将根据指定的格式字符串生成一个新的字符串,并使用可选的参数填充格式字符串中的占位符。以下是有关 String.format() 方法的更详细信息: 语法 public stati…...

【Mysql】关联查询1对多处理
关联查询1对多返回 遇见的问题 审批主表,和审批明细表,一张审批对应多张明细数据,每条明细数据的状态是不一样的,现在需要根据明细的状态获取到主单子的状态,状态返回矩阵如下 明细状态返回总状态都是已完成已完成都…...

vue 入门案例模版
vue 入门案例1 01.html <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title> &l…...
el-select实现懒加载
先看一个线上的演示示例:https://code.juejin.cn/pen/7273352811440504889 背景 我们在实际开发中经常遇到这样的需求: el-select实现懒加载,用通俗的话说,为了增加响应速度,就是初始下拉只展示50条数据,…...

Java泛型机制
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏:每天一个知识点 ✨特色专栏:…...
Linux CentOS安装抓包解包工具Wireshark图形化界面
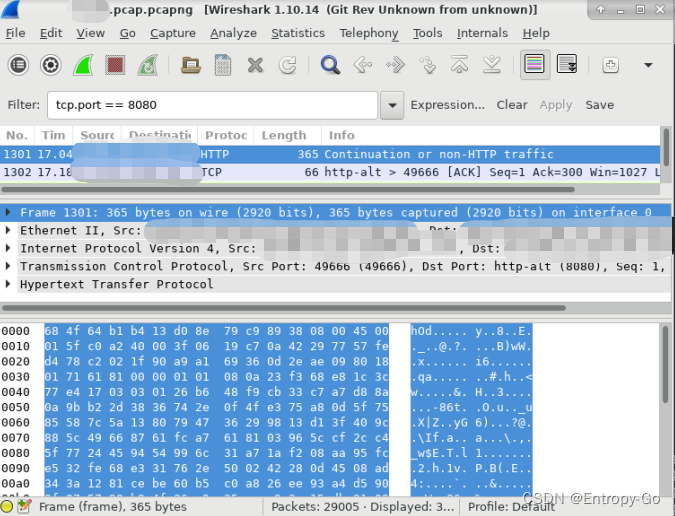
1.Wireshark介绍 Wireshark 是一个开源的网络协议分析工具,它能够捕获和分析网络数据包,提供深入的网络故障排除、网络性能优化和安全审计等功能。它支持跨多个操作系统,包括 Windows、macOS 和 Linux。 2.Wireshark主要使用方法 捕获数据…...

虹科分享 | 温度边缘效应对冻干成品含水量的影响(下)——优化和总结
上一篇文章中介绍到借助虹科Ellab的温度记录仪观察到由于冻干机壁面温度的影响,形成的边缘效应导致同一隔板的不同区域冻干饼块的干燥程度不均匀,含水量不同。 06 初次试验结果: 二次干燥中的产品温度显示: 放置在搁板中间的产品…...
安全通告 TFV-1 (CVE-2016-10319))
ATF(TF-A)安全通告 TFV-1 (CVE-2016-10319)
安全之安全(security)博客目录导读 ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-1 (CVE-2016-10319) 二、CVE-2016-10319 一、ATF(TF-A)安全通告 TFV-1 (CVE-2016-10319) Title 错误的固件更新SMC可能导致意外的大数据拷贝到安全内存中 CVE ID CVE-2016-10319 …...

说说我最近筛简历和面试的感受。。
大家好,我是鱼皮。 都说现在行情不好、找工作难,但招人又谈何容易?! 最近我们公司在招开发,实习社招都有。我收到的简历很多,但认真投递的、符合要求的却寥寥无几,而且都是我自己看简历、选人…...
)
Mysql /etc/my.cnf参数详解(一)
[mysqld] #server相关 server_id176452388 //每个MySQL服务器都需要具有唯一的server_id值 super_read_only 0 //不开启只读,在slave节点会开启即super_read_only 1 port 3306 //指定了Mysql开放的端口; default-storage-engine InnoDB skip-name…...

用最少数量的箭引爆气球【贪心算法】
用最少数量的箭引爆气球 有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。 一支弓箭可以沿着 x 轴从不同点 完全垂直 地…...
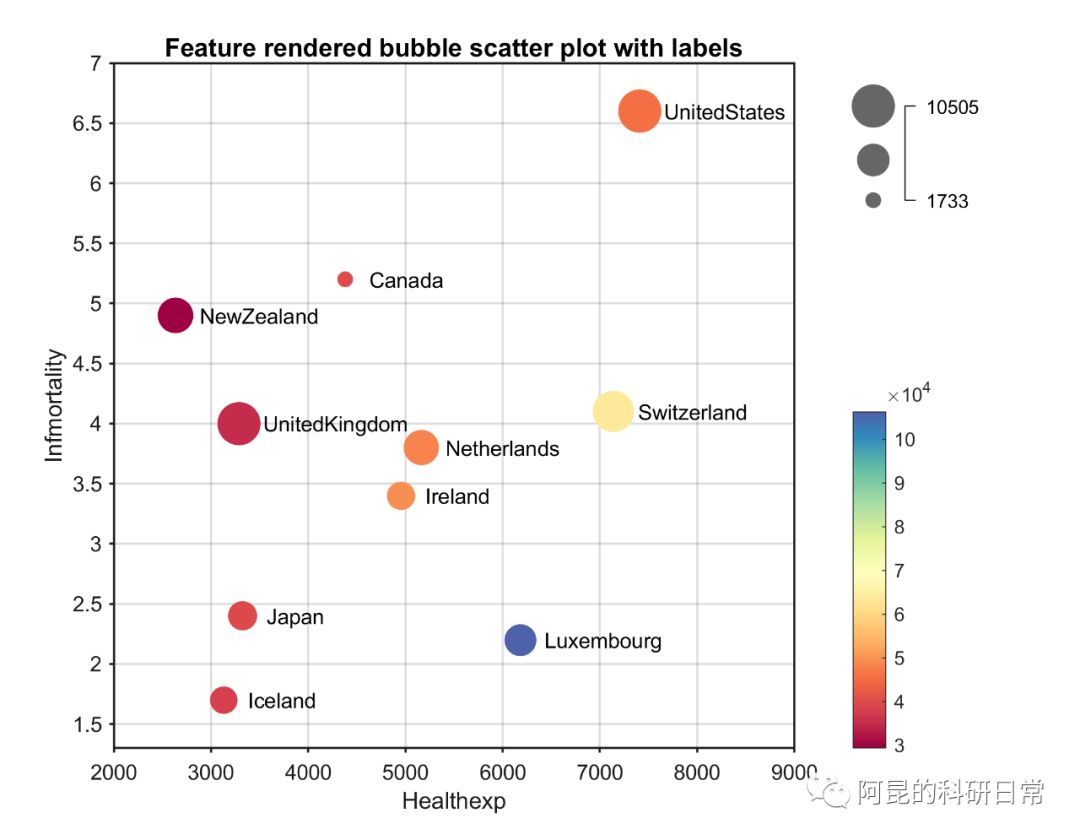
Matlab论文插图绘制模板第109期—特征渲染的标签气泡散点图
在之前的文章中,分享了Matlab标签散点图的绘制模板: 特征渲染的标签散点图: 进一步,再来分享一下特征渲染的标签气泡散点图的绘制模板,从而可以再添加一个维度的信息。 先来看一下成品效果: 特别提示&…...

音视频 ffplay命令播放媒体
播放本地文件 ffplay -window_title "test time" -ss 2 -t 10 -autoexit test.mp4 ffplay buweishui.mp3播放网络流 ffplay -window_title "rtmp stream" rtmp://202.69.69.180:443/webcast/bshdlive-pc强制解码器 mpeg4解码器:ffplay -vco…...

使用Fiddler模拟网络
Fiddler已经预置提供了模拟Modem速度的选项,其位置位于: Rules->Performances->Simulate Modem Speeds 勾选该选项后,所有通过Fiddler代理的流量都会变得用56k modem上网一般。 要直观观察限速后的效果,最好使用运行在浏览…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
