[递归] 子集 全排列和组合问题
1.1 子集I

思路可以简单概括为 二叉树,每一次分叉要么选择一个元素,要么选择空,总共有n次,因此到n+1进行保存结果,返回。像这样:

#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
int n;
vector<int >temp;
vector<vector<int> > result;
void DFS(int m){if (m == n+1){result.push_back(temp);return ;}//选择元素mtemp.push_back(m);DFS(m+1);//继续递归temp.pop_back();//返回//选择空DFS(m+1);
}bool cmp(vector<int > &a,vector<int > &b){if (a.size()!=b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d",&n);DFS(1);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;
}最后自己编写比较函数,简单来说,vector大小相同时,可以直接按照< >这些比较符号进行比较。大小不同时,则按照vector大小进行排序,这里按照题目要求均是小于。
1.2 子集II

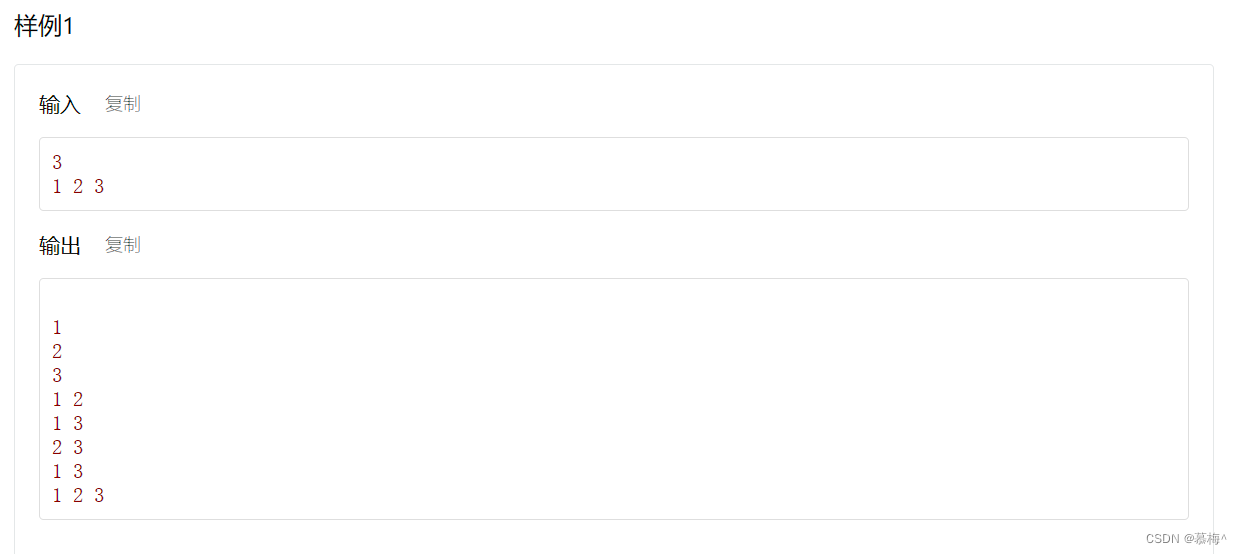

区别在于,自己给定一些元素,进行排序。
那么只需要用一个数组存储这些元素,在压栈/出栈时,换成对应的数组元素即可,思路一致。
代码几乎没有变化。
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> temp;
vector<vector<int> > result;
const int N =15;
int q[N];
int n;
void DFS(int m){if (m==n+1){result.push_back(temp);return ;}temp.push_back(q[m]);DFS(m+1);temp.pop_back();DFS(m+1);
}
bool cmp(vector<int> &a ,vector<int> &b){if (a.size()!= b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d",&n);for (int i=1;i<=n;i++)scanf("%d",&q[i]);DFS(1);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}1.3 子集III


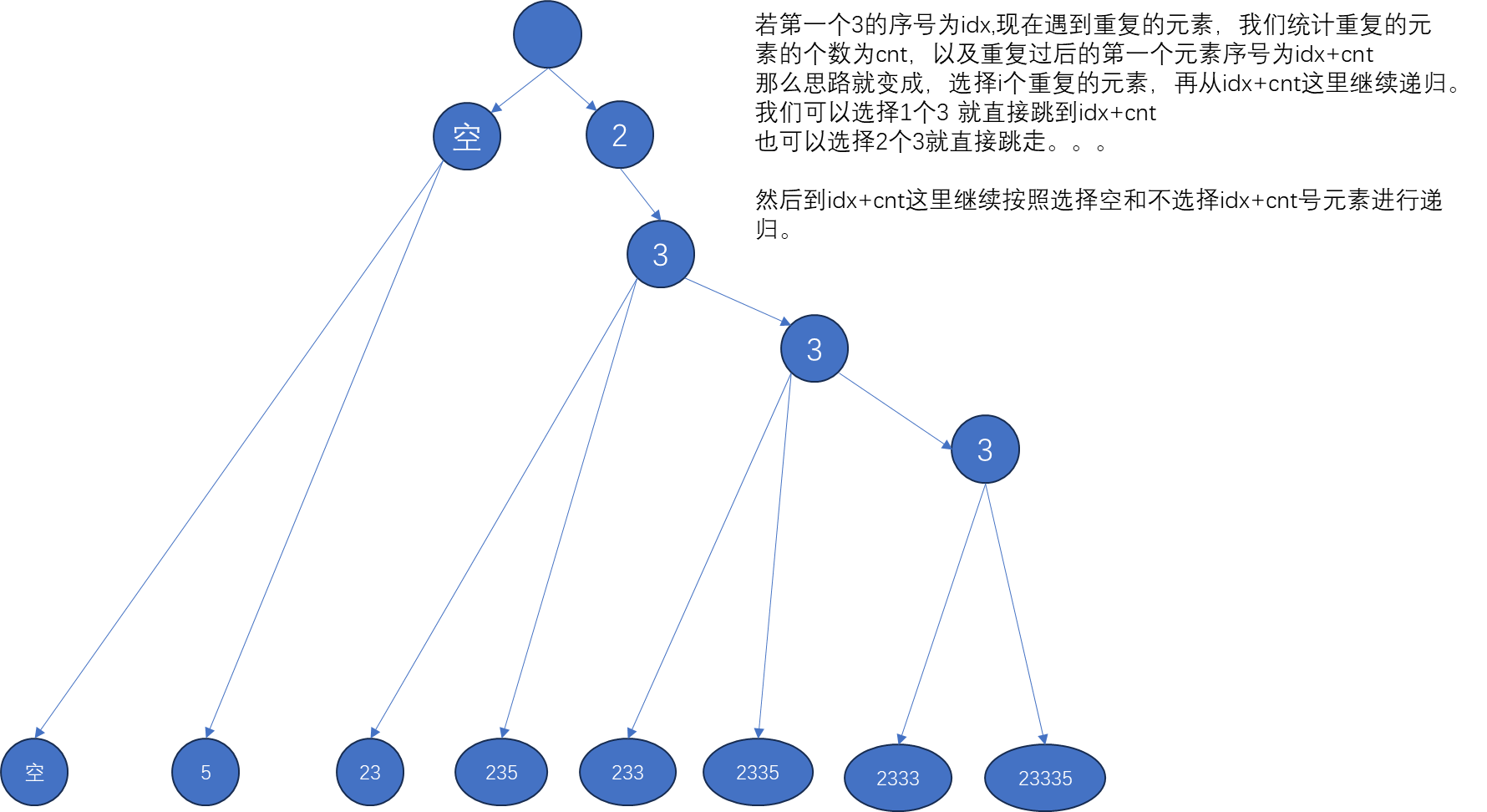
思路还是二叉树深搜递归,但是由于会出现重复的数,按照之前的输出会重复输出一些值,例如样例里的1的子集都会输出两边,因为代码并没有认为第一个1与第二个1是不同的。
首先输入的序列是升序的,因此我们可以连续地处理这些重复的元素。
例如 2 3 3 3 5
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> temp;
vector<vector<int> > result;
const int N =15;
int q[N];
int n;
void DFS(int idx){if (idx==n+1){result.push_back(temp);return ;}int cnt=1;while (idx<n && q[idx]==q[idx+1]){cnt++;idx++;}//经过该循环,idx = 最后一个重复元素的序号,cnt为重复元素的个数// 选择空 DFS(idx+1);//选择重复元素for (int i=1;i<=cnt;i++){temp.push_back(q[idx]);DFS(idx+1);// 选择重复的元素为 1 2 3 ....cnt个}//在这个循环中,我们将之前添加到 temp 中的元素逐个移除,//以回溯到不添加这些重复元素的情况for (int i=1;i<=cnt;i++){temp.pop_back();}
}
bool cmp(vector<int> &a ,vector<int> &b){if (a.size()!= b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d",&n);for (int i=1;i<=n;i++)scanf("%d",&q[i]);DFS(1);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}2.1 全排列I

思路很简单,给个图:

设置个q[]表示其是否被使用过,依次递归,返回时再赋值0;
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> temp;
vector<vector<int> > result;
int n;
const int N = 10;
int q[N]={0};
void DFS(int m){if (m == n+1){result.push_back(temp);}for (int i=1;i<=n;i++){if (!q[i]){temp.push_back(i);q[i]=1;DFS(m+1);q[i]=0;temp.pop_back();}}}
bool cmp(vector<int> &a ,vector<int> &b){if (a.size()!=a.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d",&n);DFS(1);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}2.2 全排列II
思路依旧简单,全排列I是用i作为正整数,这次是给定正整数压栈和出栈,q[]来储存输入的数,flag[]来表示其是否被使用过,代码相同
#include <cstdio>
#include <algorithm>
#include <vector>using namespace std;
int n;
const int N=10;
int q[N];
int flag[N] = {0};
vector<int> temp;
vector<vector<int> > result;
void DFS(int m){if (m==n+1){result.push_back(temp);}for (int i=1;i<=n;i++){if (!flag[i]){temp.push_back(q[i]);flag[i]=1;DFS(m+1);flag[i]=0;temp.pop_back();}}}
bool cmp(vector<int> &a,vector<int> &b){if (a.size()!=b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d",&n);for (int i=1;i<=n;i++)scanf("%d",&q[i]);DFS(1);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}2.3 全排列III


如果按照之前的思路,那么样例1会出现大量重复,与子集的解决方法类似,不过是这里是记录每个数的个数,使用cnt[]进行计算,并且每个数只记录一次;
1 1 3 : 只取最后一个重复的id进行记录次数,像这样:cnt[1] = 0 cnt[2]=2 cnt[3] =1
那么全排列就很简单,每次的全排列对于q[i]的数只能用cnt[i]次数。
那么每次for循环
for (int i=1;i<=n;i++){if (cnt[i]){temp.push_back(q[i]);cnt[i]--;DFS(m+1);cnt[i]++;temp.pop_back();}}只能用一次重复的值
#include <cstdio>
#include <algorithm>
#include <vector>using namespace std;
int n;
const int N = 10;
int q[N];
int cnt[N]={0};
vector<int> temp;
vector<vector<int> >result;
void DFS(int m){if (m==n+1){result.push_back(temp);return ;}for (int i=1;i<=n;i++){if (cnt[i]){temp.push_back(q[i]);cnt[i]--;DFS(m+1);cnt[i]++;temp.pop_back();}}
}
bool cmp(vector<int> &a,vector<int> &b){if (a.size()!=b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d",&n);for (int i=1;i<=n;i++)scanf("%d",&q[i]);for (int i=1;i<=n;i++){int j=i;cnt[i]=1;while (j<=n && q[j]==q[j+1]){cnt[i]++;j++;}i = j;}DFS(1);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}3.1 组合I

和全排列很像,不过全排列是有顺序的(样例中3 4 和4 3在全排列均是有效的),而组合是无序的,因此我们在挑选的时候可以人为地进行有序限制,从而不会重复。
思路与这道递归题类似
[递归] 自然数分解之方案数_慕梅^的博客-CSDN博客
我们保证后一个数要大于前一个这样的要求,那么就可实现组合题。
样例2中 两个数x y 满足(x<y)
那我们的DFS(int m),m则是后面的数需要大于的序号
DFS(0)可以作为入口
#include <cstdio>
#include <algorithm>
#include <vector>using namespace std;
int n,k;
const int N = 15;vector<int> temp;
vector<vector<int> > result;void DFS(int m){if (temp.size()==k){//递归的出口则改为vector <int> temp的大小==kresult.push_back(temp);return ;}for (int i=m+1;i<=n;i++){//循环从 序号m+1开始temp.push_back(i);DFS(i);//将i作为参数进行下一次的递归temp.pop_back();}return ;}
bool cmp(vector<int> &a,vector<int> &b){if (a.size()!=b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d%d",&n,&k);DFS(0);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}
3.2 组合II
需要自己输入序列,思路不变

#include <cstdio>
#include <algorithm>
#include <vector>using namespace std;
int n,k;
const int N = 15;
int q[N];
vector<int> temp;
vector<vector<int> > result;void DFS(int m){if (temp.size()==k){result.push_back(temp);return ;}for (int i=m+1;i<=n;i++){temp.push_back(q[i]);DFS(i);temp.pop_back();}
}
bool cmp(vector<int> &a,vector<int> &b){if (a.size()!=b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d%d",&n,&k);for (int i=1;i<=n;i++)scanf("%d",&q[i]);DFS(0);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}
3.3 组合III
可以借鉴全排列的思想,使用cnt来进行计数
#include <cstdio>
#include <algorithm>
#include <vector>using namespace std;
int n,k;
const int N = 15;
int q[N];
int cnt[N]={0};
vector<int> temp;
vector<vector<int> > result;void DFS(int m){if (temp.size()==k){result.push_back(temp);return ;}for (int i=m;i<=n;i++){//i从m开始,因为有重复的元素。if (cnt[i]){cnt[i]--;temp.push_back(q[i]);DFS(i);cnt[i]++;temp.pop_back();}}
}
bool cmp(vector<int> &a,vector<int> &b){if (a.size()!=b.size())return a.size()<b.size();return a<b;
}
int main(){scanf("%d%d",&n,&k);for (int i=1;i<=n;i++)scanf("%d",&q[i]);for (int i=1;i<=n;i++){int j = i;cnt[i] = 1;while ((j+1)<=n&&q[j]==q[j+1]){cnt[i]++;j++;}i = j;}DFS(0);sort(result.begin(),result.end(),cmp);for (int i=0;i<result.size();i++){for (int j=0;j<result[i].size();j++){if (j==result[i].size()-1)printf("%d",result[i][j]);else printf("%d ",result[i][j]);}printf("\n");}return 0;}
不过与前两个组合不同的是
for (int i=m+1;i<=n;i++){条件因改为
for (int i=m;i<=n;i++){如果不该与,之前的序列都是没有重复的元素,因此可以下一次的序号需要+1以保证大于前面的数,然而这里有重复的元素,因此从m开始。
相关文章:

[递归] 子集 全排列和组合问题
1.1 子集I 思路可以简单概括为 二叉树,每一次分叉要么选择一个元素,要么选择空,总共有n次,因此到n1进行保存结果,返回。像这样: #include <cstdio> #include <vector> #include <algorithm&…...
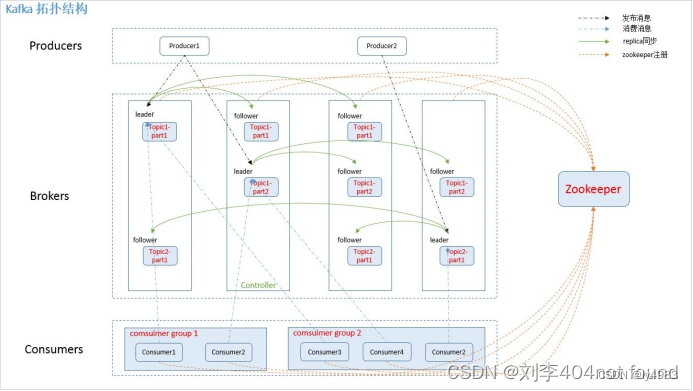
ELK安装、部署、调试(四)KAFKA消息队列的安装和部署
1.简介 Kafka是一种高吞吐量的分布式发布订阅消息系统,它可以处理消费者在网站中的所有动作流数据。 这种动作(网页浏览,搜索和其他用户的行动)是在现代网络上的许多社会功能的一个关键因素。 这些数据通常是由于吞吐量的要求而通…...

半导体晶片机器视觉测量及MARK点视觉定位
半导体晶片机器视觉测量及MARK点视觉定位 客户的需求: 检测内容: SMT行业晶片位置角度与PCB板Mark点位置的测试测量 检测要求: 精度0.04mm,移动速度100mm/s 视觉可行性分析: 对样品进行了光学实验,并进行图像处理,…...
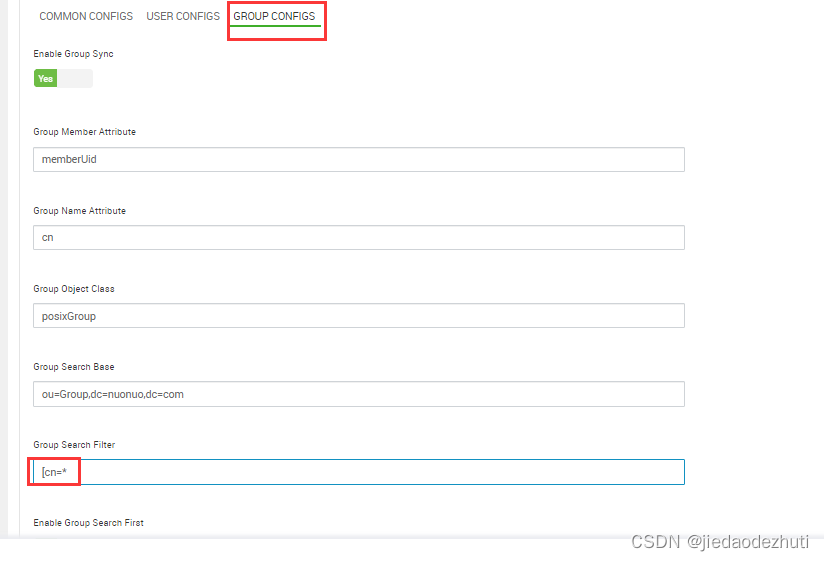
ranger无法同步用户问题解决
1.首先就是定位日志,日志目录 cd /var/log/ranger/usersync 定位到问题报错如下: LdapDeltaUserGroupBuilder.getUsers() failed with exception:java.naming.AuthticationExceptiom :[LDAP:error code 49 - Invalid Credentials]:remaing name ‘ouPeople,dc*.dccom’ 解决办法…...
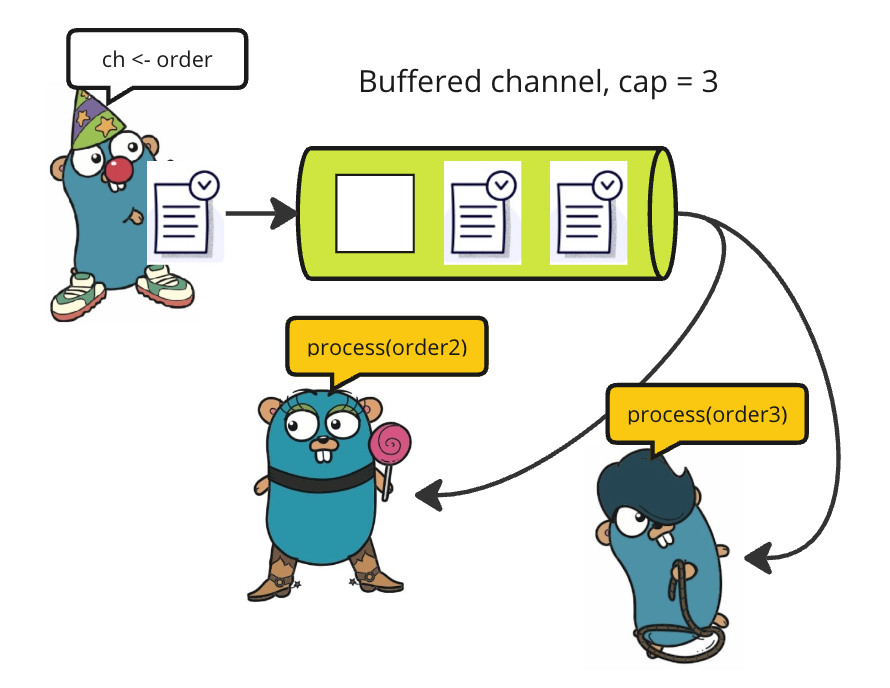
使用通信顺序进程(CSP)模型的 Go 语言通道
在并发编程中,许多编程语言采用共享内存/状态模型。然而,Go 通过实现 通信顺序进程(CSP)模型来区别于众多。在CSP中,程序由不共享状态的并行进程组成;相反,它们通过通道进行通信和同步操作。因此…...

VPN网关
阿里云VPN网关(VPN Gateway,简称VPN)是一款基于Internet,通过加密通道将企业数据中心、办公网或终端与专有网络(VPC) 安全可靠连接起来的服务。 VPN网关提供IPsec-VPN和SSL-VPN两种。 网络连接方式应用场景IPsec-VPN支持在企业本地数据中心、企业办公网…...

产品展示视频制作的要点
制作产品展示视频时通过精心策划的视频剧本和拍摄手法,可以准确地呈现活动的目的、主题和特点,让观众更好地理解和认同活动的意义。深圳产品活动视频制作公司老友记小编还为您整理了以下一些重要的制作要点: 1.明确目标受众:了解你…...

appium+python自动化测试
获取APP的包名 1、aapt即Android Asset Packaging Tool,在SDK的build-tools目录下。该工具可以查看apk包名和launcherActivity 2、在android-sdk里面双击SDK-manager,下载buidl-tools 3、勾选build-tools,随便选一个版本,我这里选的是24的版…...

【AI辅助办公】PDF转PPT,移除水印
PDF转PPT 将PDF上传链接即可转换成PPT。 https://www.camscanner.com/pdftoppthttps://www.camscanner.com/pdftoppt移除水印 第一步:打开视图-宏 第二步:输入宏名(可以是人以文字…...
ssm农业视频实时发布管理系统源码
ssm农业视频实时发布管理系统源码108 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm package com.controller;import java.io.File; import java.io.FileNotFoundException; import java.io.IOException; impo…...

【100天精通python】Day48:python Web开发_WSGI接口与使用
目录 1 WSGI接口 1.1 CGI 简介 1.2 WSGI 简介 1.3 定义 WSGI 接口 1.3.1 应用程序(Application) 1.3.2 服务器(Server) 1.4 WSGI 接口的使用示例 1.5 WSGI接口的优势 1 WSGI接口 上一节实现了静态服务器,但是当…...

Understanding Lockup Cells
工具会分析扫描链和EDT逻辑之间的控制时序元素的时钟的时序关系,当必须要同步时钟并保持数据完整性时插入边沿触发寄存器(lockup cells)。 可以使用report_edt_lockup_cells命令来展示工具已经插入的lockup cells的详细报告。 Lockup Cell Insertion 工具会分析控制时序元…...
javaCV实现java图片ocr提取文字效果
引入依赖: <dependency><groupId>org.bytedeco</groupId><artifactId>javacv-platform</artifactId><version>1.5.5</version></dependency> 引入中文语言训练数据集:chi_sim GitHub - tesseract-ocr…...
七牛云OSS存储
前言: 七牛云的存储项目的附件,需要开发一套七牛云的工具类,可以使用该工具类进行七牛云服务器进行文件的上传与下载操作; 七牛云的文档学习: 相关的依赖项的配置: <dependency><groupId>com.amazonaws</groupId><artifactId>aws-java-sdk-s3…...
11.物联网lwip,网卡原理
一。LWIP协议栈内存管理 1.LWIP内存管理方案 (1)堆heap 1.灰色为已使用内存 2.黑色为未使用内存 3.紫色为使用后内存 按照某种算法,把数据放在内存块中 (2)池pool 设置内存池,设置成大小相同的内存块。 2…...
视频监控/视频汇聚/视频云存储EasyCVR平台接入华为ivs3800平台提示400报错,该如何解决?
开源EasyDarwin视频监控TSINGSEE青犀视频平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,在视频监控播放上,视频云存储/安防监控汇聚平台可支持1、4、9、16个画面窗口播放,可同时播放多路视频…...
WordPress主题Zing V2.2.1/模块化WordPress响应式通用企业商城主题
WordPress主题Zing V2.2.1,模块化WordPress响应式通用企业商城主题。 功能介绍 百度熊掌号文章实时推送、原创保护 多设备支持自适应布局,支持电脑、Pad、手机以及各种浏览器 SEO优化首页、文章、页面、分类均支持自定义标题、关键字和描述 速度优化…...

【无需公网IP】在树莓派上搭建Web站点
目录 1.概述 2.使用 Raspberry Pi Imager 安装 Raspberry Pi OS 3.设置 Apache Web 服务器 3.1测试 web 站点 3.2安装静态样例站点 3.3将web站点发布到公网 3.4安装 Cpolar 3.5cpolar进行token认证 3.6生成cpolar随机域名网址 3.7生成cpolar二级子域名 3.8将参数保存…...
出差在外,远程访问企业局域网象过河ERP系统「内网穿透」
文章目录 概述1.查看象过河服务端端口2.内网穿透3. 异地公网连接4. 固定公网地址4.1 保留一个固定TCP地址4.2 配置固定TCP地址 5. 使用固定地址连接 概述 ERP系统对于企业来说重要性不言而喻,不管是财务、生产、销售还是采购,都需要用到ERP系统来协助。…...
Vue2-replace属性、编程式路由导航、缓存路由组件、两个新的生命周期钩子、路由守卫、路由器工作模式
🥔:如果事与愿违,那一定是上天另有安排 更多Vue知识请点击——Vue.js VUE2-Day13 router-link的replace属性编程式路由导航1、什么是编程式路由导航2、如何编码3、使用案例示例说明 缓存路由组件两个新的生命周期钩子路由守卫1、路由元信息2、…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
