遗传算法及Python实现
0 建议学时
4学时
1 人工智能概述
2020中国人工智能产业年会在苏州召开,会上发布的《中国人工智能发展报告2020》显示,过去十年(2011-2020) ,中国人工智能专利申请量达389571件,占全球总量的74.7%,位居世界第一。
报告指出,中国在自然语言处理、芯片技术、机器学习等10多个人工智能子领域的科研产出水平居于世界前列。

人工智能被认为是二十一世纪三大尖端技术(基因工程、纳米科学、人工智能)之一。
人工智能的基石是数学,而这些数学算法的实现是由一个一个的函数组合得来。比如,我们计算 sin(πhr2)\sin (\pi hr^2)sin(πhr2) 可以得到圆柱体的体积的正弦值。对于前述公式,我们就可以将其分解为3个简单的乘法和一个正弦函数。在编程语言中,我们也把这些函数称为方法。目前流行的人工神经网络,实际上就是由几百甚至几千个方法构成。通过定义方法不仅可以实现简单的数学公式,还可以实现一些无法用数学公式描述的算法,如遗传算法。人工智能的三大要素:
- 数据
- 算法
- 算力
2 遗传算法
一种通过模拟自然进化过程搜索最优解的方法。遗传算法是一种仿生算法,最主要的思想是物竞天择,适者生存。这个算法很好的模拟了生物的进化过程,保留好的物种,同样一个物种中的佼佼者才会幸运的存活下来。转换到数学问题中,这个思想就可以很好的转化为优化问题,在求解方程组的时候,好的解视为好的物种被保留,坏的解视为坏的物种而淘汰,设置好进化次数以后开始迭代,记录下这些解里面最好的那个,就是要求解的方程组的解。
遗传算法是类比自然界的达尔文进化实现的简化版本。
达尔文进化论的原理概括总结如下:
- 变异:种群中单个样本的特征(性状,属性)可能会有所不同,这导致了样本彼此之间有一定程度的差异;
- 遗传:某些特征可以遗传给其后代。导致后代与双亲样本具有一定程度的相似性;
- 选择:种群通常在给定的环境中争夺资源。更适应环境的个体在生存方面更具优势,因此会产生更多的后代。
2.1 基本概念
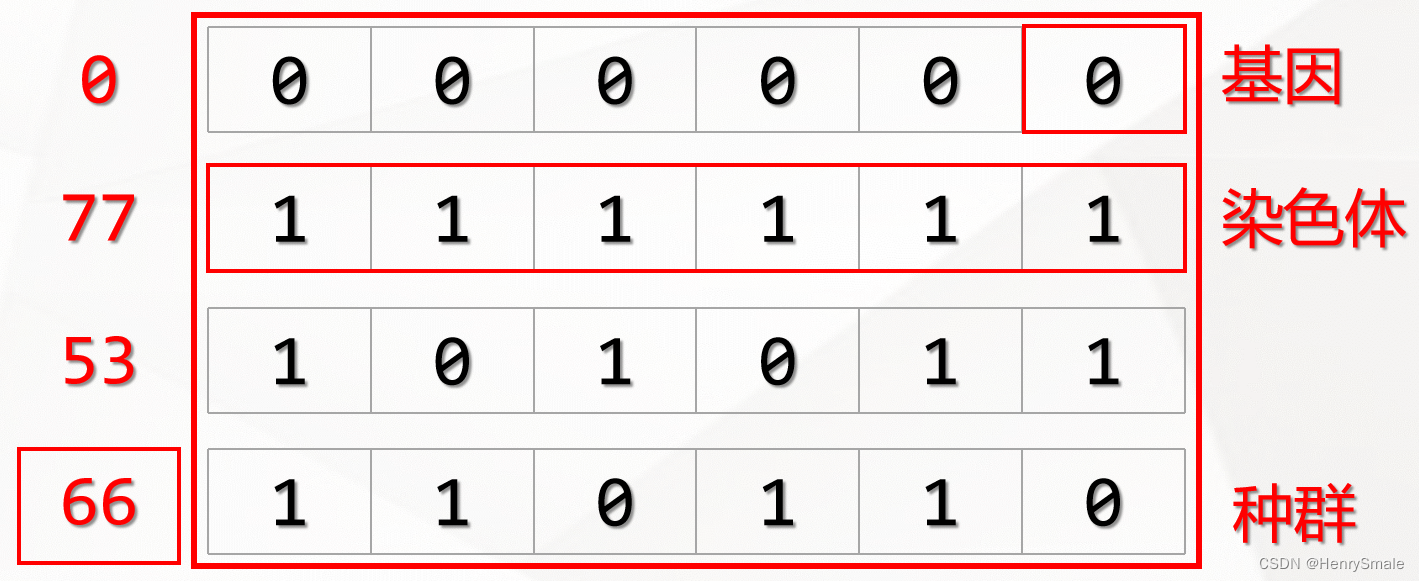
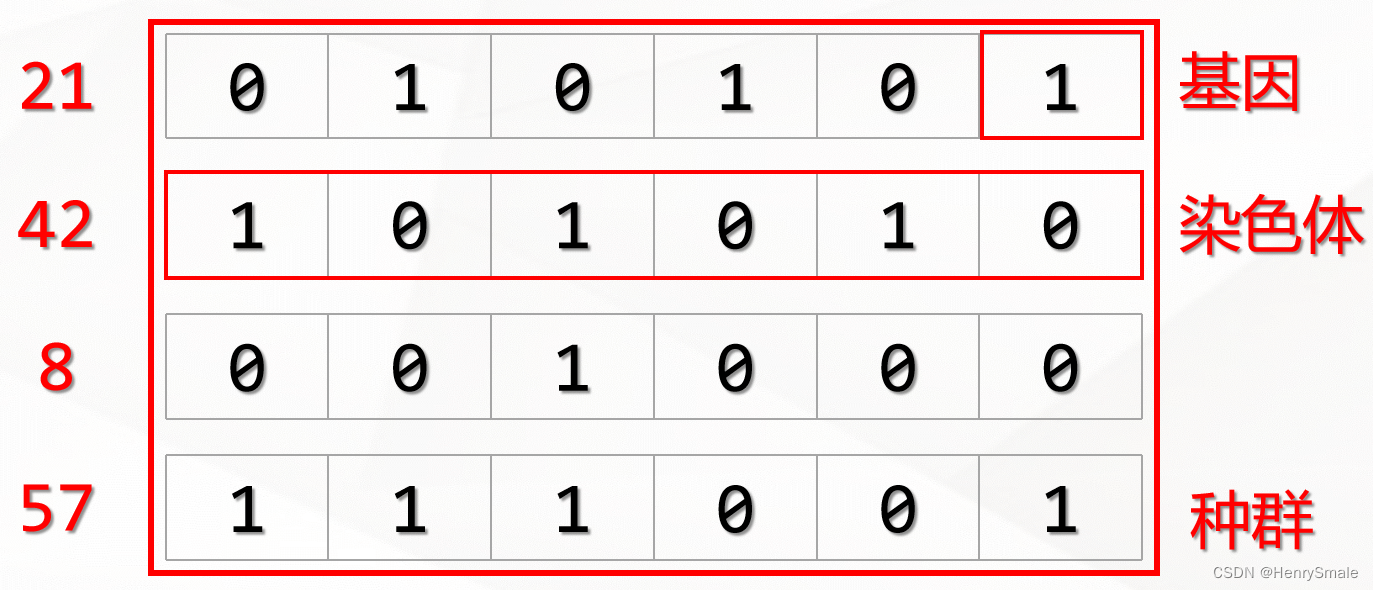
2.1.1 基因和染色体

在遗传算法中,我们首先需要将要解决的问题映射成一个数学问题,也就是所谓的“数学建模”,那么这个问题的一个可行解即被称为一条“染色体”。一个可行解一般由多个元素构成,那么这每一个元素就被称为染色体上的一个“基因”。
比如说,对于如下函数而言,[1,2,3]、[1,3,2]、[3,2,1]均是这个函数的可行解(代进去成立即为可行解),那么这些可行解在遗传算法中均被称为染色体。
3x+4y+5z<1003x+4y+5z<100 3x+4y+5z<100
这些可行解一共有三个元素构成,那么在遗传算法中,每个元素就被称为组成染色体的一个基因。
2.1.2 适应度函数
在自然界中,似乎存在着一个上帝,它能够选择出每一代中比较优良的个体,而淘汰一些环境适应度较差的个人。那么在遗传算法中,如何衡量染色体的优劣呢?这就是由适应度函数完成的。适应度函数在遗传算法中扮演者这个“上帝”的角色。
遗传算法在运行的过程中会进行N次迭代,每次迭代都会生成若干条染色体。适应度函数会给本次迭代中生成的所有染色体打个分,来评判这些染色体的适应度,然后将适应度较低的染色体淘汰掉,只保留适应度较高的染色体,从而经过若干次迭代后染色体的质量将越来越优良。
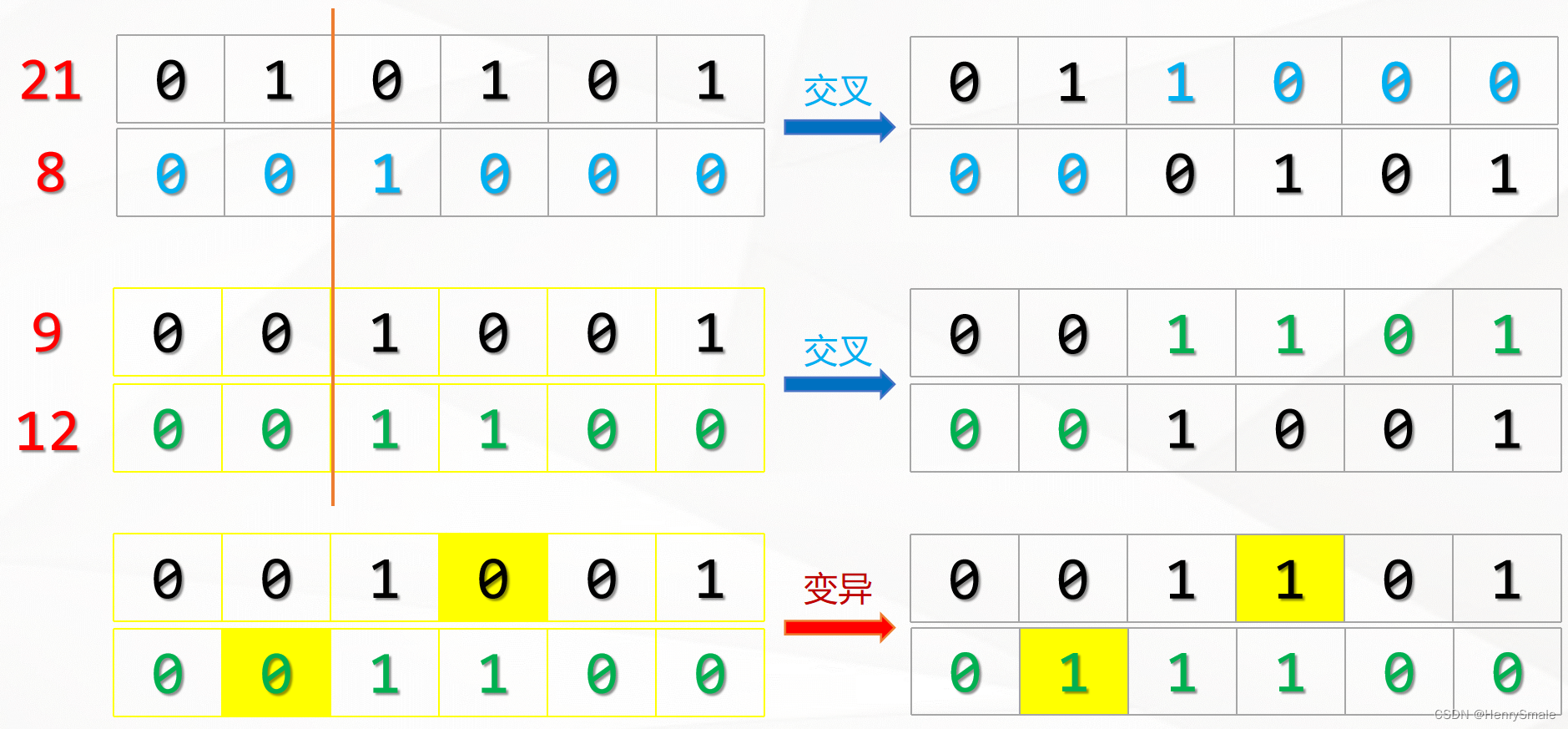
2.1.3 交叉
遗传算法每一次迭代都会生成N条染色体,在遗传算法中,这每一次迭代就被称为一次“进化”。那么,每次进化新生成的染色体是如何而来的呢?——答案就是“交叉”,你可以把它理解为交配。
交叉的过程需要从上一代的染色体中寻找两条染色体,一条是爸爸,一条是妈妈。然后将这两条染色体的某一个位置切断,并拼接在一起,从而生成一条新的染色体。这条新染色体上即包含了一定数量的爸爸的基因,也包含了一定数量的妈妈的基因。
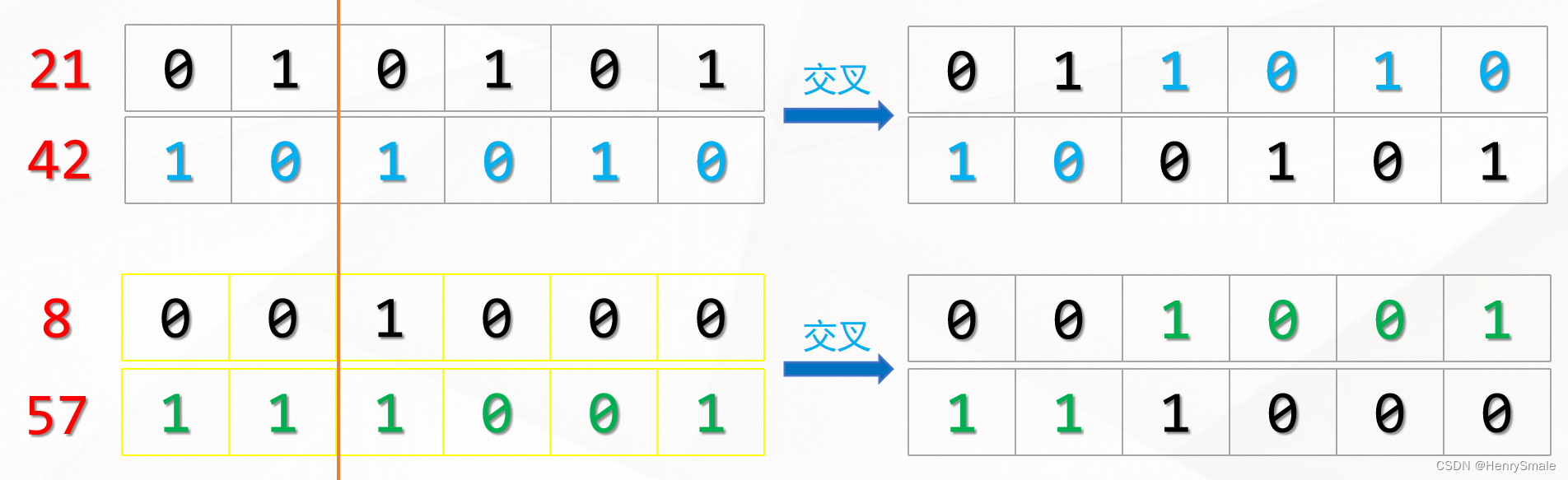
那么,如何从上一代染色体中选出爸爸和妈妈的基因呢?这不是随机选择的,一般是通过轮盘赌算法完成。
在每完成一次进化后,都要计算每一条染色体的适应度,然后采用如下公式计算每一条染色体的适应度概率。那么在进行交叉过程时,就需要根据这个概率来选择父母染色体。适应度比较大的染色体被选中的概率就越高。这也就是为什么遗传算法能保留优良基因的原因。
染色体i被选择的概率 = 染色体i的适应度 / 所有染色体的适应度之和
2.1.4 变异
交叉能保证每次进化留下优良的基因,但它仅仅是对原有的结果集进行选择,基因还是那么几个,只不过交换了他们的组合顺序。这只能保证经过N次进化后,计算结果更接近于局部最优解,而永远没办法达到全局最优解,为了解决这一个问题,我们需要引入变异。
变异很好理解。当我们通过交叉生成了一条新的染色体后,需要在新染色体上随机选择若干个基因,然后随机修改基因的值,从而给现有的染色体引入了新的基因,突破了当前搜索的限制,更有利于算法寻找到全局最优解。

2.1.5 复制
每次进化中,为了保留上一代优良的染色体,需要将上一代中适应度最高的几条染色体直接原封不动地复制给下一代。
假设每次进化都需生成NNN条染色体,那么每次进化中,通过交叉方式需要生成N−MN-MN−M条染色体,剩余的MMM条染色体通过复制上一代适应度最高的M条染色体而来。
2.2 通过例子说明进化过程
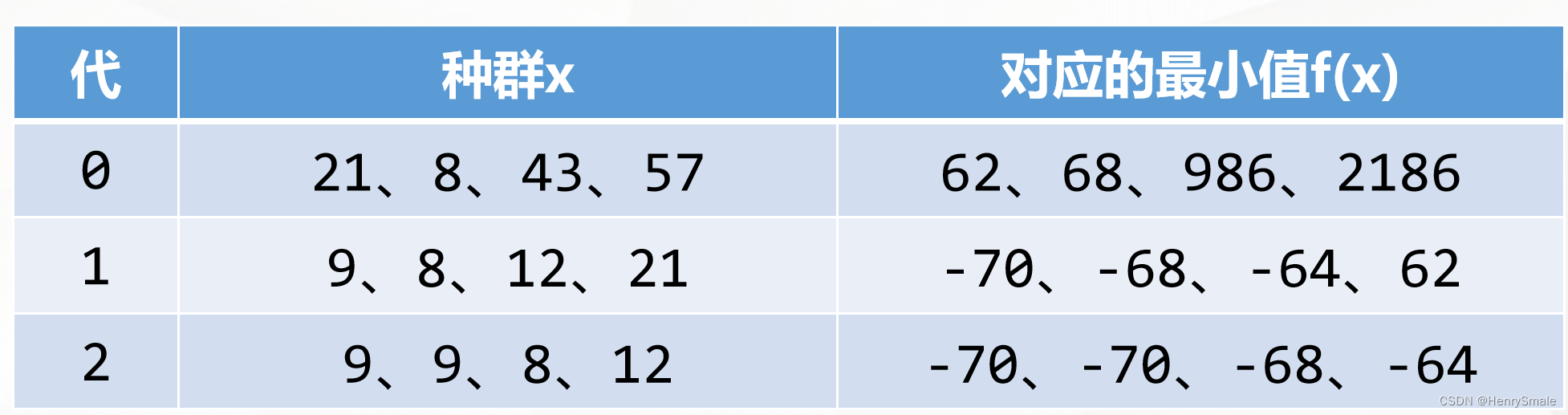
求f(x)=x2−19x+20f(x)=x^2-19x+20f(x)=x2−19x+20的最小值,其中x=1,…,64x=1,…,64x=1,…,64之间的整数。
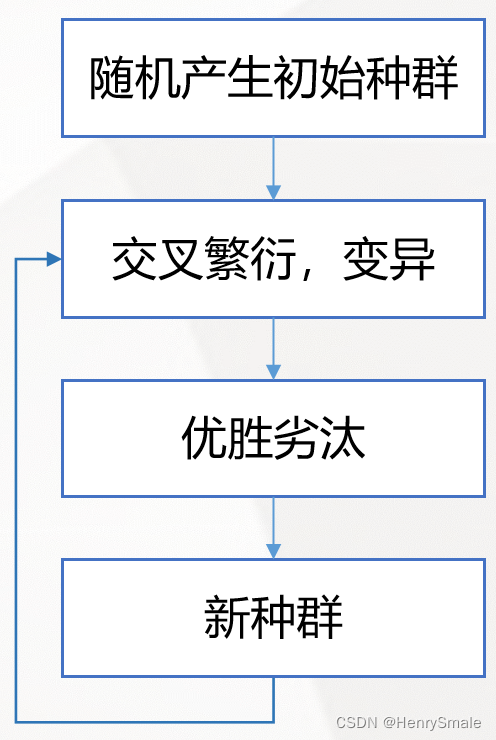
2.2.1 第一轮
随机产生初始种群
交叉繁衍,变异
优胜劣汰

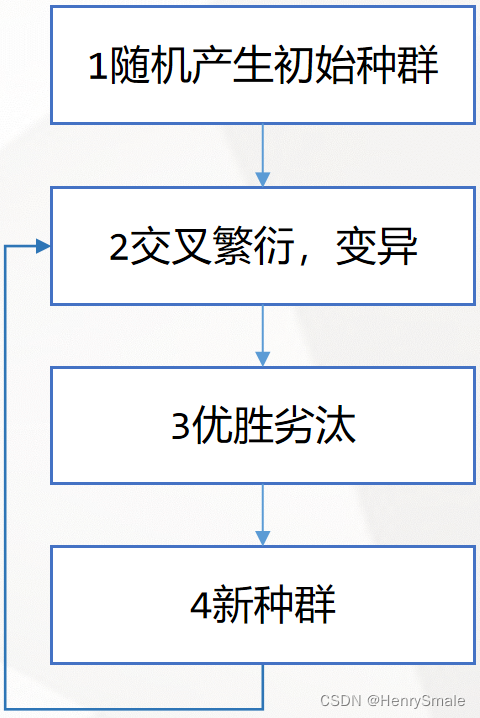
流程图
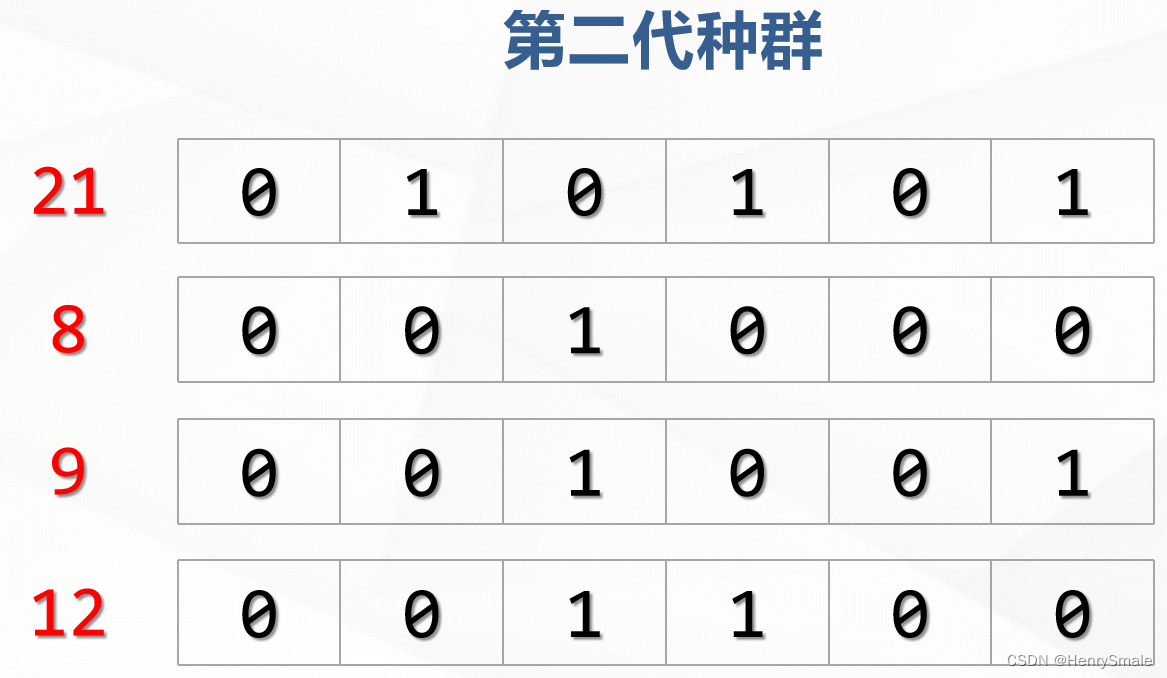
2.2.2 第二轮
交叉繁衍,变异
优胜劣汰

3 如何编写<遗传算法计算最小值>的程序?
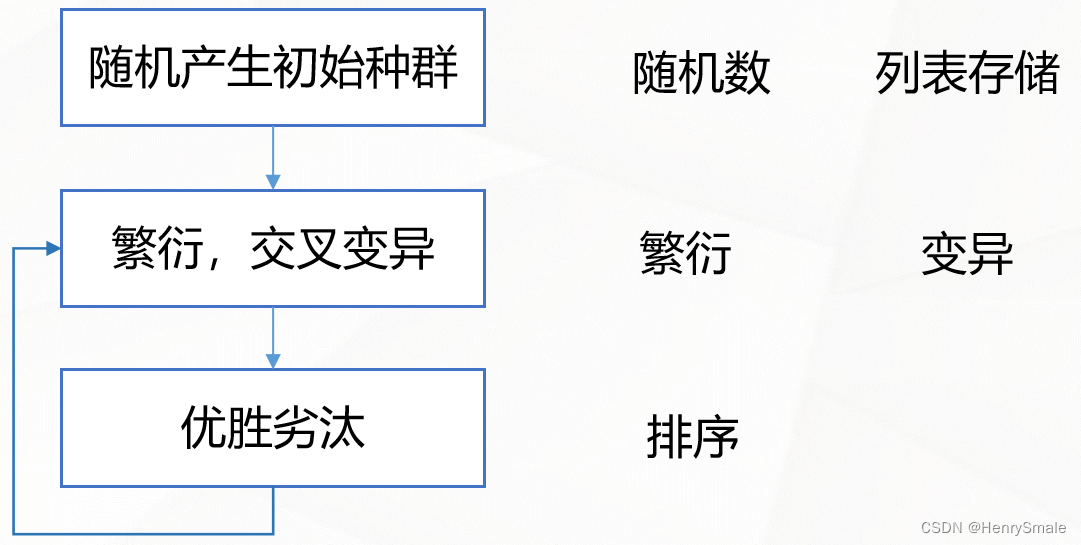
根据流程图写出步骤,每个步骤标号:
细化所有的步骤,直到能和代码对应为止。
如何设计函数?哪些代码应该封装为函数?
3.1 基础知识回顾
- 复习1:函数定义
def fact(n):s = 1for i in range(1, n+1):s*= ireturn s
- 复习2:函数调用
a=fact(5)
print(a)
- 复习3:匿名函数

sum = lambda a,b: a+b
print(sum(1 , 3)) #调用函数打印其返回值
3.2 模块设计
3.3 核心代码
3.3.1 随机产生初始种群
lt=[21,42,8,57]
3.3.2 繁衍,交叉变异

# 繁衍,交换基因,x,y是数据,pos是从第几位开始交换
def exchange(x, y, pos):xstr = '{0:06b}'.format(x) # 转换为6位二进制ystr = '{0:06b}'.format(y) # 转换为6位二进制tempxstr = '0b' + xstr[:pos] + ystr[pos:] # 临时存放tempystr = '0b' + ystr[:pos] + xstr[pos:] # 临时存放return int(tempxstr, 2), int(tempystr, 2) # 再转换为十进制

# 交叉变异
def mutate(x, pos):xstr = '{0:06b}'.format(x) # 转换为6位二进制if xstr[pos] == '0':xstr = xstr[:pos] + '1' + xstr[pos + 1:]else:xstr = xstr[:pos] + '0' + xstr[pos + 1:]return int(xstr, 2)
3.3.3 总体代码
import random# 交叉变异
def mutate(x, pos):xstr = '{0:06b}'.format(x) # 转换为6位二进制if xstr[pos] == '0':xstr = xstr[:pos] + '1' + xstr[pos + 1:]else:xstr = xstr[:pos] + '0' + xstr[pos + 1:]return int(xstr, 2)# 繁衍,交换基因,x,y是数据,pos是从第几位开始交换
def exchange(x, y, pos):xstr = '{0:06b}'.format(x) # 转换为6位二进制ystr = '{0:06b}'.format(y) # 转换为6位二进制tempxstr = '0b' + xstr[:pos] + ystr[pos:] # 临时存放tempystr = '0b' + ystr[:pos] + xstr[pos:] # 临时存放return int(tempxstr, 2), int(tempystr, 2) # 再转换为十进制lt=[21,42,8,57]
#lt=[1,2,3,4]
for gen in range(0,10): #次数为代数son1,son2=exchange(lt[0],lt[1],3) #1、2号繁衍2个后代,加入ltlt.append(son1)lt.append(son2)son3,son4=exchange(lt[2],lt[3],3) #3、4号繁衍2个后代,加入ltlt.append(son3)lt.append(son4)son5=mutate(lt[2],random.randint(0,5)) #根据第3个父数据变异lt.append(son5)son6=mutate(lt[3],random.randint(0,5)) #根据第4个父数据变异lt.append(son6)lt=sorted(lt,key=lambda x:x*x-19*x+20) #根据目标函数排序print("第{}代的种群为{}".format(gen+1,lt))ls=lt[:4]lt=lsx=lt[0]
print("最小的X是{},对应的y值为{}".format(x,x*x-19*x+20))
3.3.4 运行结果
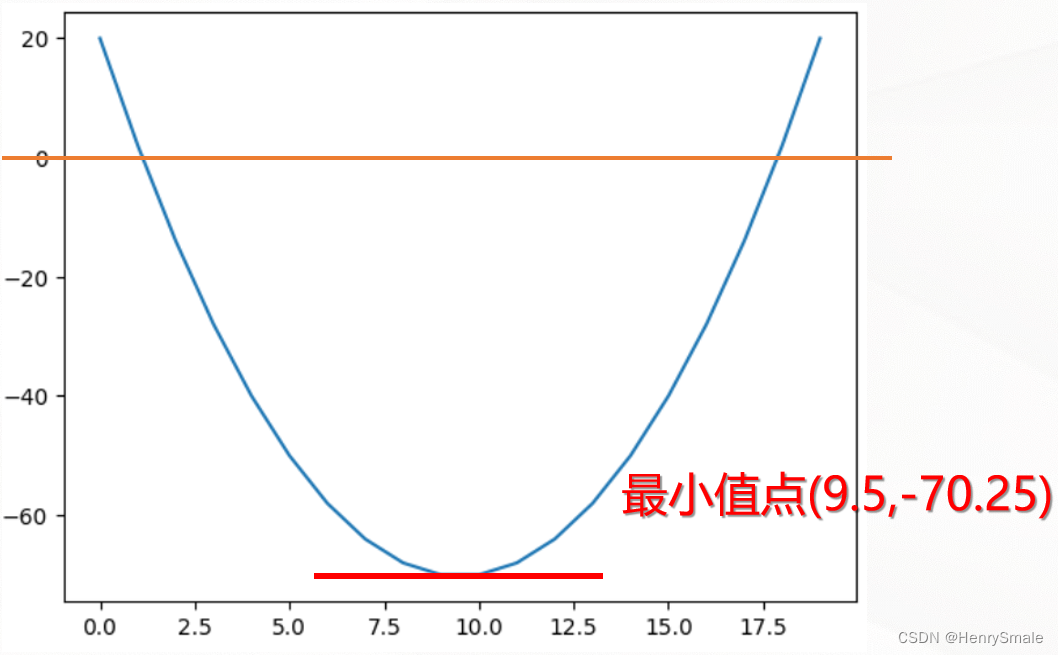
第1代的种群为 [9, 8, 12, 21, 26, 37, 41, 42, 56, 57]
第2代的种群为 [9, 9, 8, 8, 8, 12, 5, 5, 21, 28]
第3代的种群为 [9, 9, 9, 9, 8, 8, 8, 8, 12, 24]
第4代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第5代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第6代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第7代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第8代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第9代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
第10代的种群为 [9, 9, 9, 9, 9, 9, 9, 9, 13, 25]
最小的X是9,对应的y值为-70
3.4 思考与拓展
3.4.1 初始种群的规模与生成规则
初始种群:1,2,3,4
第1代的种群为[7, 4, 4, 3, 3, 2, 2, 1, 1, 20]
第2代的种群为[7, 7, 4, 4, 4, 4, 3, 3, 0, 19]
第3代的种群为[7, 7, 7, 7, 4, 4, 4, 4, 0, 20]
第4代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第5代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第6代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第7代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第8代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第9代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
第10代的种群为[7, 7, 7, 7, 7, 7, 7, 7, 3, 23]
最小的X是7,对应的y值为-64
初始种群:21,42,36,54,1,6421,42,36,54,\color{red}{1,64}21,42,36,54,1,64
第1代的种群为[9, 8, 12, 4, 15, 21, 26, 37, 41, 42, 52, 56, 57, 59, 63]
第2代的种群为[9, 9, 8, 8, 8, 12, 12, 5, 4, 15, 4, 17, 20, 21, 31]
第3代的种群为[9, 9, 9, 9, 8, 8, 8, 8, 8, 8, 8, 12, 12, 12, 24]
第4代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 8, 8, 8, 8, 12, 13, 25]
第5代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第6代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第7代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第8代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第9代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
第10代的种群为[9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 13, 13, 25]
最小的X是9,对应的y值为-70
3.4.2 遗传规则的设计:交叉、变异
采用随机数生成变异基因的位置
s=random.randint(0,5)\color{red}{\mathbf{s=random.randint(0,5)}}s=random.randint(0,5) #随机取0-5中任意数
#变异
def mutate(x):s=random.randint(0,5) #随机取0-5中任意数fb='{0:06b}'.format(x) #转换为6位二进制if fb[pos]=='0':sb=fb[:s] + '1' + fb[s+1:]else:sb=fb[:s] + '0' + fb[s+1:]return int(sb,2)
4 课后延伸
- 启发式算法还包含:蚁群算法、模拟退火算法等,调研这些算法,并撰写报告;
- 请编写遗传算法部分的总结报告,包含:
(1)遗传算法的原理
(2)遗传算法的流程
(3)举一个计算实例说明其原理
(4)如何编写遗传算法的代码
(5)该算法的优缺点及如何改进
相关文章:

遗传算法及Python实现
0 建议学时 4学时 1 人工智能概述 2020中国人工智能产业年会在苏州召开,会上发布的《中国人工智能发展报告2020》显示,过去十年(2011-2020) ,中国人工智能专利申请量达389571件,占全球总量的74.7%,位居世界第一。 报…...

零基础 Ubuntu 20.04.01 下搭建51单片机开发环境[开源编译器SDCC]
原创首发于CSDN,转载请注明出处,谢谢! 文章目录为何会在Linux下开发单片机个人系统环境与所用开发板安装开源编译器 sdccSTC MCU ISP 闪存工具 stcgal 的安装单片机代码的编译与测试|编写主代码 main.c|使用 sdcc 编译…...

手摸手快速入门 正则表达式 (Vue源码中的使用)
vue2源码 在 vue2 源码的 src\compiler\parser\html-parser.js 文件中 里面有大量的正则表达式,如下图 可以看到非常的长,不是我说,就前几行,如果没有相关的 正则表达式 的工具,我可能就被劝退了😭 这里…...

TCP/IP网络协议族分成及其每层作用
1、可以分为应用层、传输层、网络层、链路层 2、各层的作用 应用层(可以想象成是快递打包过程) 决定了向用户提供应用服务时通信的活动,将要进行的操作或者数据进行一个打包。 传输层(可以理解为选择顺丰、圆通等快递公司) 提供数据传输的方…...
)
041、子序列类型问题(labuladong)
子序列类型问题 一、经典动态规划:编辑距离 基于labuladong的算法网站,经典动态规划:编辑距离; 总结: 一般来说涉及到两个字符串的问题,需要依赖上一次的各种操作,一般使用dp tableÿ…...
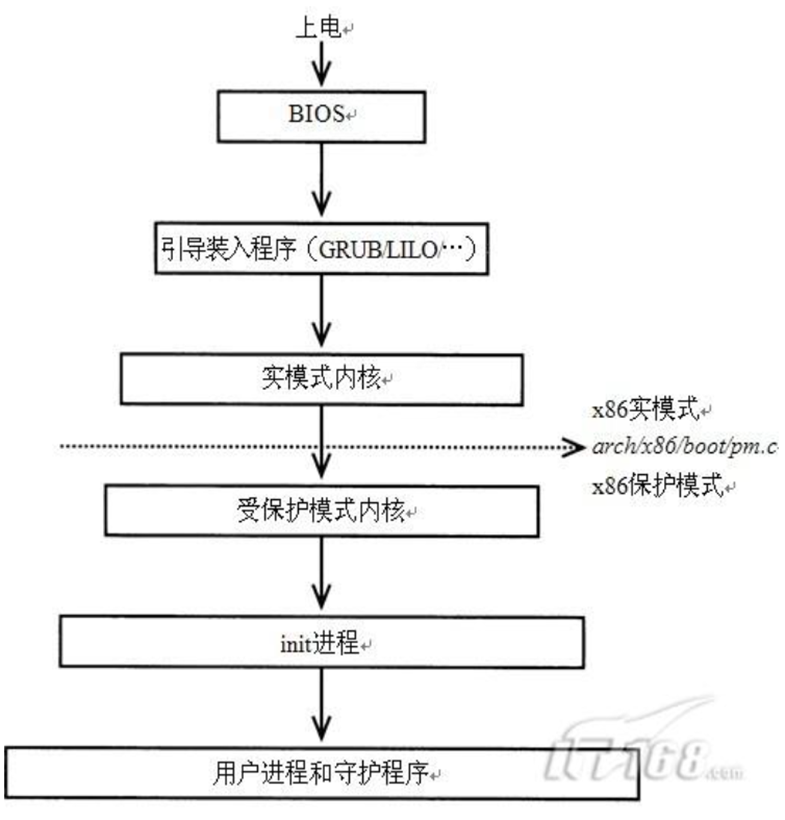
linux系统开机文段释义
第一段Version 2.01.1204. Copyright (C) 2010American Megatrends, Inc.Press <DEL> or <F2> to entersetup. Press <F7> for BBS POPUP Menu.设备上电,提示按DEL键或者F2键进入BIOS设置。按F8可以调出启动设备列表,可以选择性的启动…...

抽奖动画大转盘抽奖思路与做法
抽奖是各类营销活动中最常见的一种形式,本产品需求大致如下:转盘周围跑马灯交替闪烁,点击抽奖,大转盘旋转,调用接口获取抽奖结果,大转盘指针指向对应的奖品。高保如下图12.整体思路本需求要求跑马灯交替闪烁…...

Java实现 - 华为2016研发工程师编程题
文章目录删数字符集合数独删数 题目描述 有一个数组 a[N] 顺序存放 0 ~ N-1 ,要求每隔两个数删掉一个数,到末尾时循环至开头继续进行,求最后一个被删掉的数的原始下标位置。以 8 个数 (N7) 为例 :{ 0,1,2…...

nginx的七层负载均衡
文章目录一、负载均衡介绍二、nginx的配置文件三、实验过程总结一、负载均衡介绍 四层负载均衡 所谓四层负载均衡是指OSI七层模型中的传输层, 那么传输层Nginx已经支持TCP/IP的控制, 所以只需要对客户端的请求进行TCP/IP协议的包转发就可以实现负载, 那么他的好处是性能非常快,…...
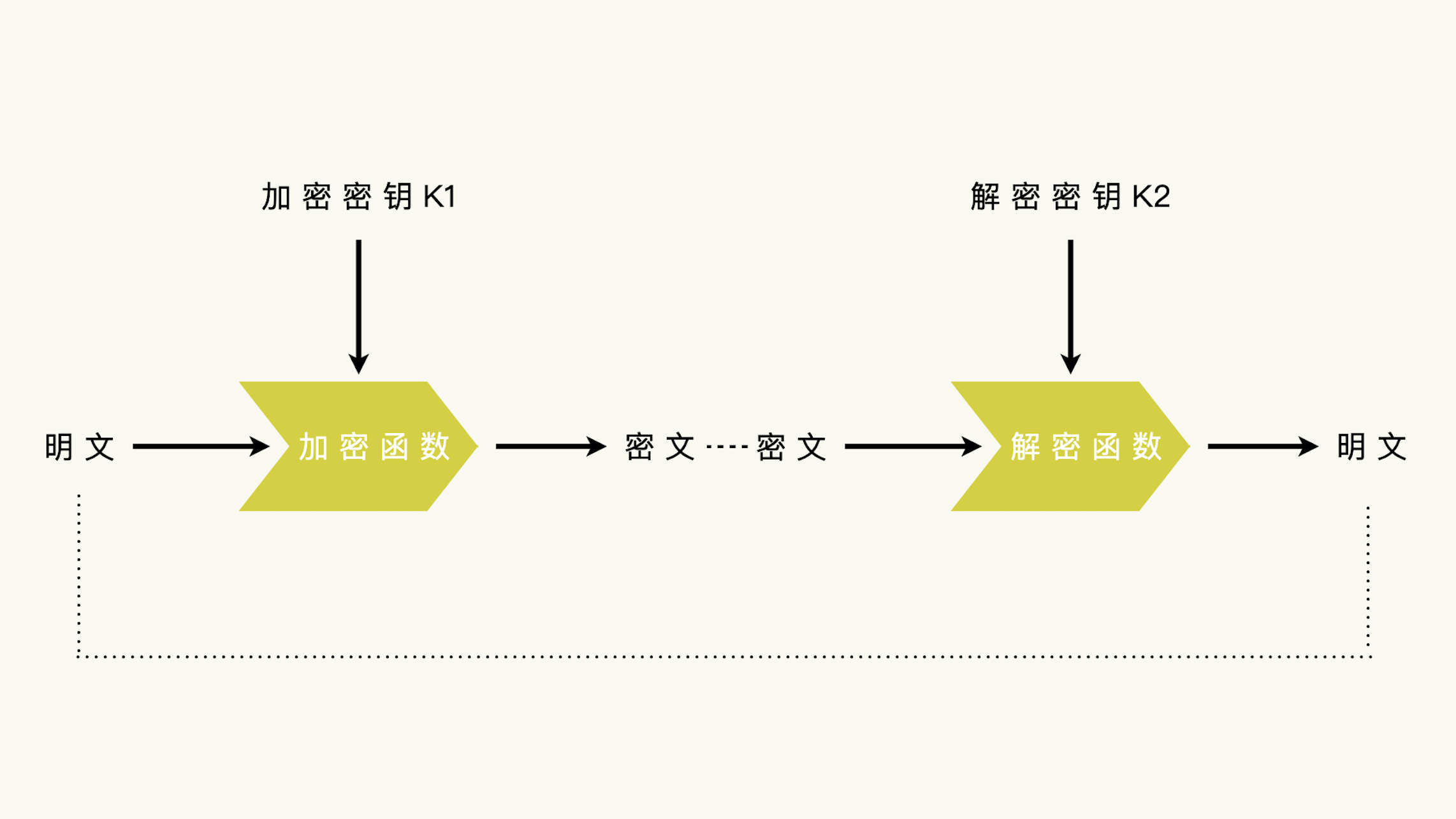
信息加密技术
介绍信息加密 信息加密是实现数据保密性的手段。 信息加密(Encryption)是将明文信息转换为密文信息,使之在缺少特殊信息时不可读的过程。只有拥有解密方法的对象,经由解密过程,才能将密文还原为正常可读的内容。 现…...

RS485通信总线详解
RS485 总线详解 RS-485 是美国电子工业协会(EIA)在 1983 年批准了一个新的平衡传输标准(Balanced Transmission Standard)也称作差分,EIA 刚开始将 RS(Recommended Standard)做为标准的前缀&am…...
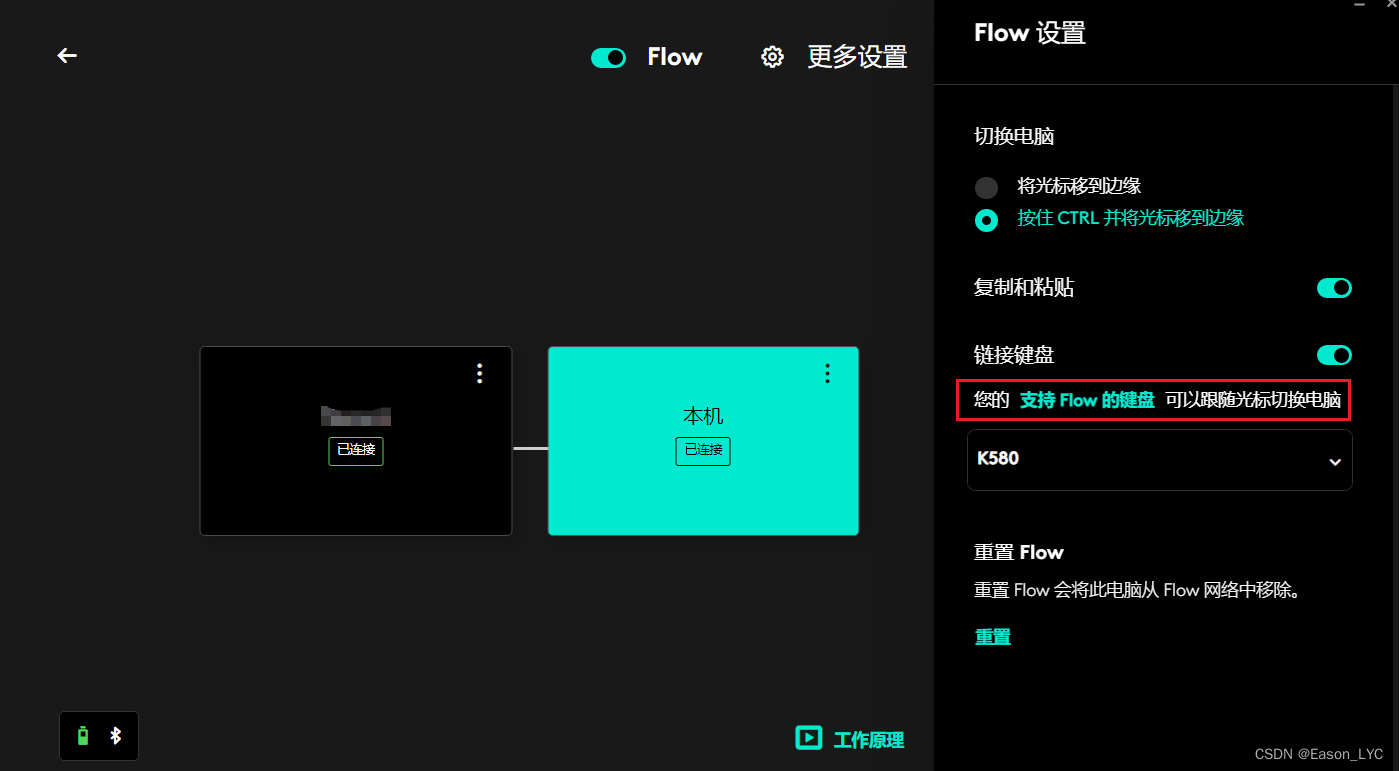
罗技LogitechFlow技术--惊艳的多电脑切换体验
作者:Eason_LYC 悲观者预言失败,十言九中。 乐观者创造奇迹,一次即可。 一个人的价值,在于他所拥有的。所以可以不学无术,但不能一无所有! 技术领域:WEB安全、网络攻防 关注WEB安全、网络攻防。…...
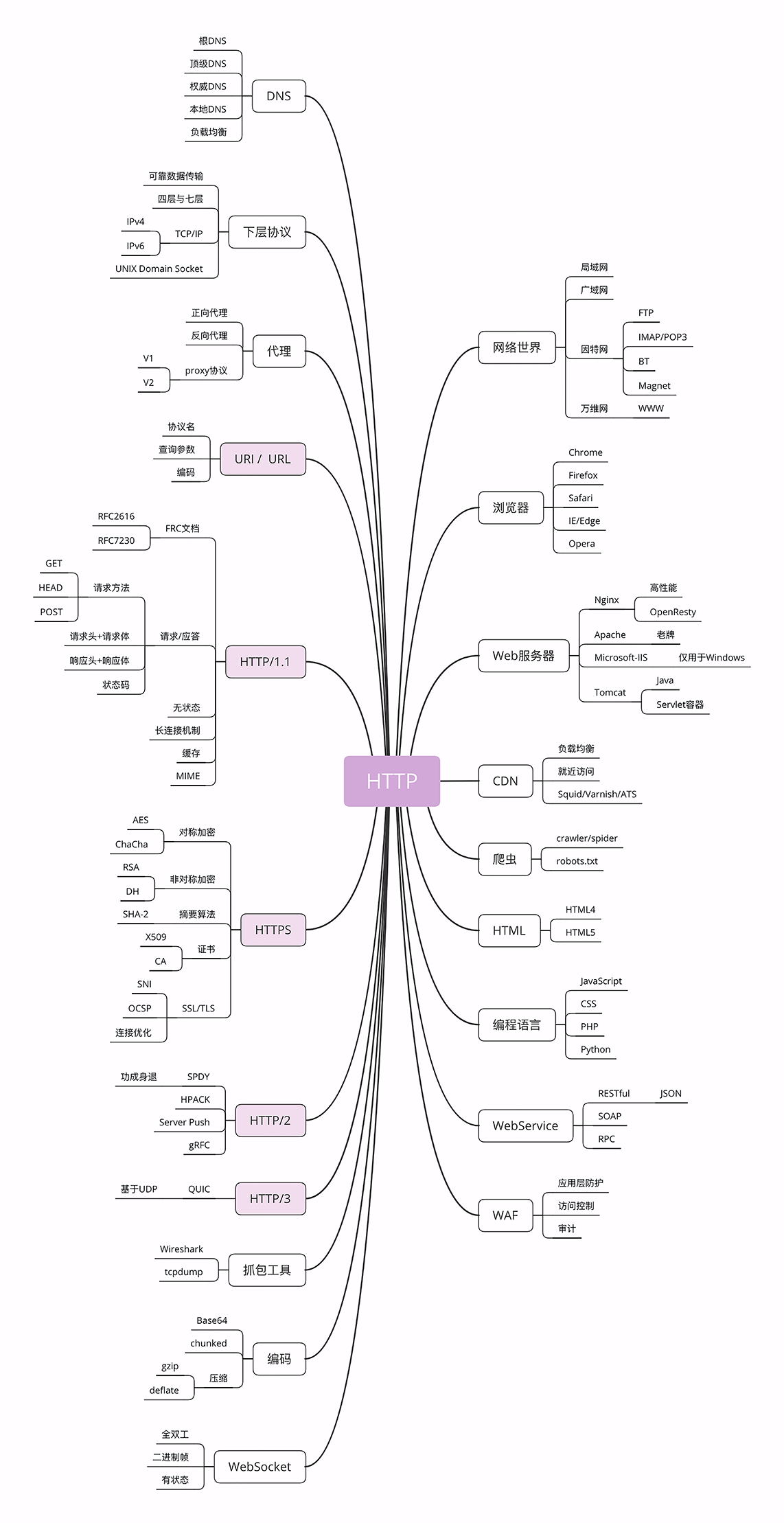
社招中级前端笔试面试题总结
HTTP世界全览 互联网上绝大部分资源都使用 HTTP 协议传输;浏览器是 HTTP 协议里的请求方,即 User Agent;服务器是 HTTP 协议里的应答方,常用的有 Apache 和 Nginx;CDN 位于浏览器和服务器之间,主要起到缓存…...

东南大学研究生上学期英语期末总结
写在前面 作者:夏日 博客地址:https://blog.csdn.net/zss192 本文为东南大学研究生英语上学期期末总结,内容为根据老师所发 PPT 总结得来 相关资料: 点我查看 题型说明 Module 1 International Conference 50% 题型范围&am…...
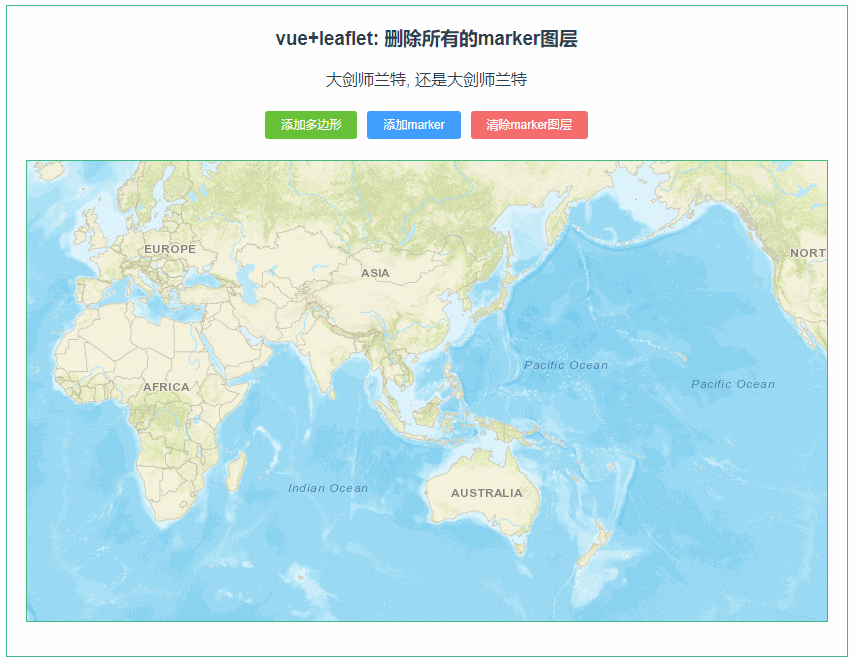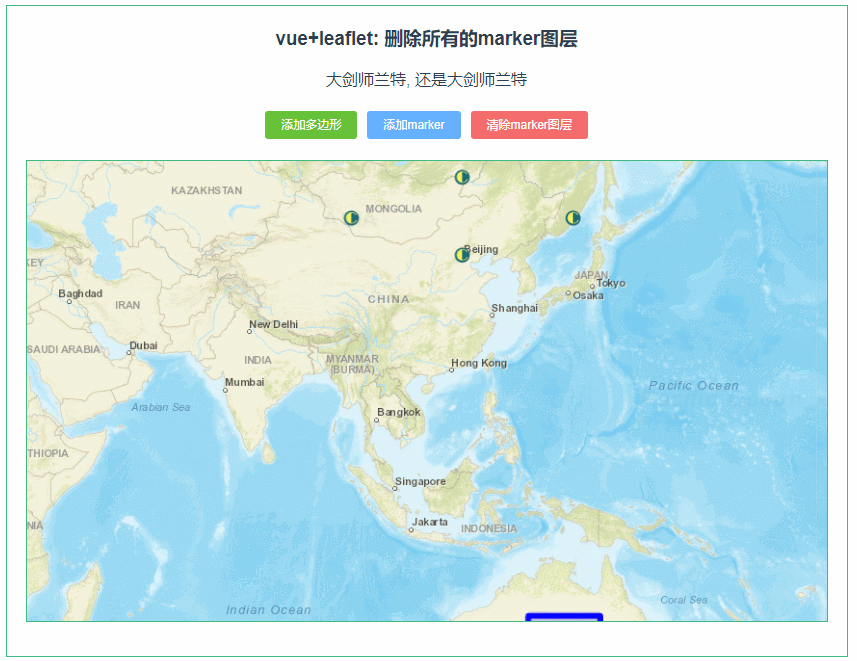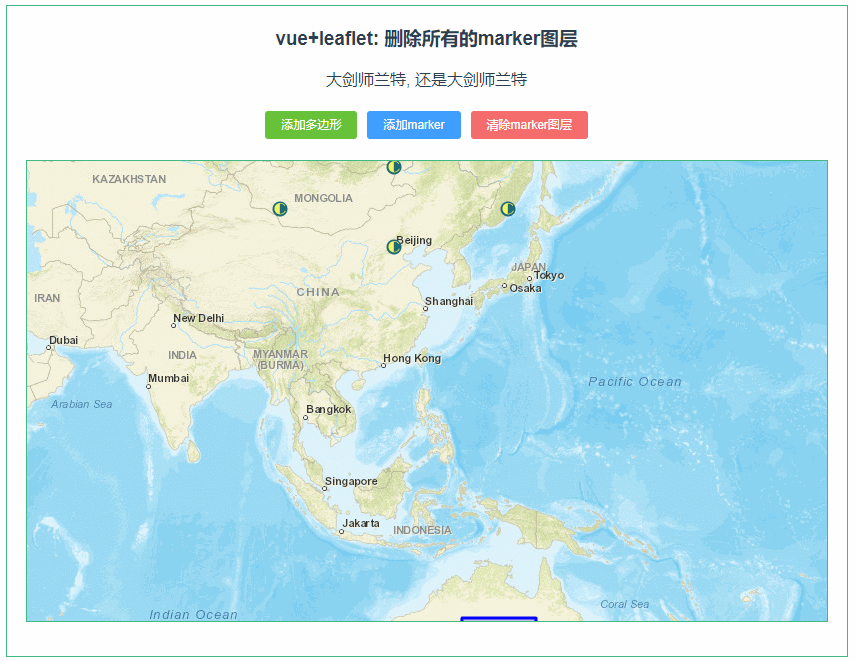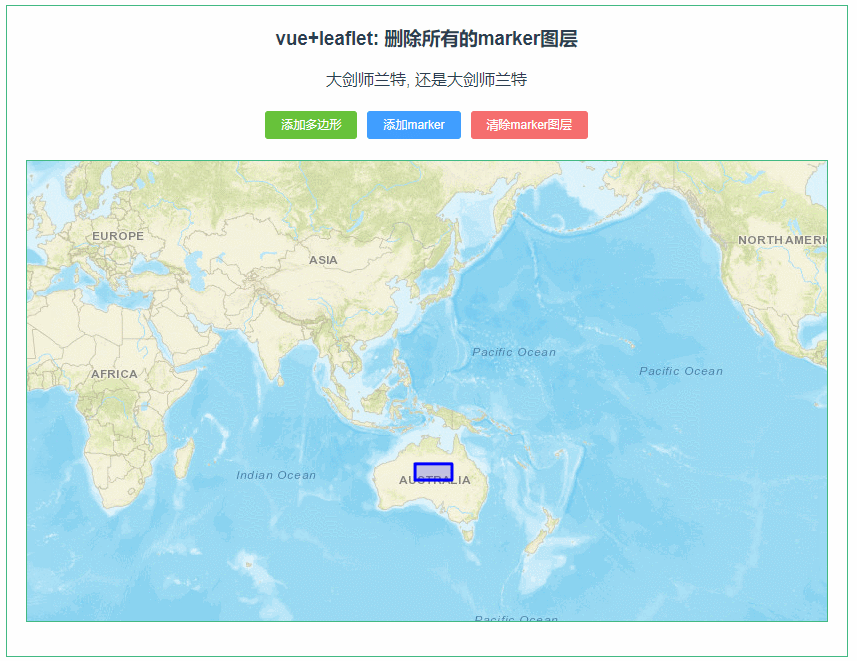
leaflet 删除所有的marker图层,保留其他图层(085)
第085个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet项目中清除所有的marker图层,保留其他图层,详情请参考源代码。这里面主要用到了(layer instanceof L.Marker ,注意 L.Marker中Marker首字母要大写。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行…...
双因素方差分析全流程
上篇文章讲述了“单因素方差分析全流程总结”,单因素方差分析只是考虑了一个自变量(定类)与一个因变量(定量)之间的关系,但是在实际问题研究中可能研究两个或者几个因素与因变量之间的关系,例如…...

微信公众号抽奖怎么做_分享微信抽奖小程序制作的好处
在H5游戏中,抽奖是最受消费者喜爱的模式之一。将H5微信抽奖活动结合到营销中,可以带来意想不到的效果,带流量和曝光率,所以许多企业也会在做活动时添加上不同类型的H5微信抽奖活动。编辑那么,新手怎么搭建微信抽奖活动…...
逻辑回归—分类问题的操作顺序
对于二元分类问题来说,分类的结果和数据的特征之间仍呈现相关关系,但是y的值不再是连续的,是0~1的跃迁。但是在这个过程中,什么仍然是连续的呢?”是概率,概率是逐渐升高的,当达到一个…...

查询服务器tns文件路径,oracle数据库tns配置方法详解
查询服务器tns文件路径,oracle数据库tns配置方法详解 TNS简要介绍与应用 Oracle中TNS的完整定义:transparence Network Substrate透明网络底层, 监听服务是它重要的一部分,不是全部,不要把TNS当作只是监听器。 TNS是Oracle Net…...

【数据结构】链表
目录 数据结构之链表:: SList.h 1.链表的概念及结构 2.链表的分类 SList.c 3.动态申请一个结点 4.单链表打印 5.单链表销毁 6.单链表头插 7.单链表头删 8.单链表尾插 9.单链表尾删 10.单链表查找 11.单链表在pos之前插入…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
