LA@齐次线性方程组解的结构
文章目录
- 齐次线性方程组解的结构🎈
- 解的性质
- 齐次线性方程组的解的线性组合还是方程组的解
- 基础解系
- 通解
- 定理:齐次线性方程组基础解系存在定理
- 齐次线性方程组的基础解系包含的向量个数(秩)👺
- 应用和示例
- 推论1
- 推论2
- 推论3:转置矩阵对的乘积秩的性质
- 非自由未知数的选取方法(最左方法)
- 基础解系和通解形式的不唯一性
- 证明
- 分析
- 证法1
- 齐次线性方程的基础解系构造
- 证明所构造的向量组是基础解系
- 证法2
- 小结
- 基础解系构造提要
- 例
- 补充
- 再给出一组上述基础解系之外的其他基础解系
- 非最左方法选取非自由变量
齐次线性方程组解的结构🎈
解的性质
齐次线性方程组的解的线性组合还是方程组的解
-
设 ξ 1 , ⋯ , ξ r \xi_1,\cdots,\xi_r ξ1,⋯,ξr都是 ( 2 ) (2) (2)的解,则 ∑ i = 1 r = k i ξ i \sum_{i=1}^r=k_i\xi_{i} ∑i=1r=kiξi
-
证明1:
-
对于齐次线性 ( 2 ) (2) (2),如果两向量 ξ 1 , ξ 2 \xi_1,\xi_2 ξ1,ξ2都是该方程组的解向量,那么对于 ξ 1 , ξ 2 \xi_1,\xi_2 ξ1,ξ2的线性组合 ξ 3 = k 1 ξ 1 + k 2 ξ 2 \xi_3=k_1\xi_1+k_2\xi_2 ξ3=k1ξ1+k2ξ2也是该方程组的解向量
- A ξ i = 0 , i = 1 , 2 A\xi_i=0,i=1,2 Aξi=0,i=1,2
- A ξ 3 = A ( ∑ i = 1 2 k i ξ i ) = ∑ i = 1 2 k i A ξ i A\xi_3=A(\sum\limits_{i=1}^{2}k_i\xi_i)=\sum\limits_{i=1}^{2}k_iA\xi_i Aξ3=A(i=1∑2kiξi)=i=1∑2kiAξi
- 而 k i A ξ i = 0 k_iA\xi_i=0 kiAξi=0,所以 A ξ 3 = 0 A\xi_3=0 Aξ3=0
-
类似的,可以得到,齐次线性方程组的解的线性组合还是方程组的解
-
-
证明2:
- 两个解向量的和仍然是解向量,再证明解向量的 k k k倍仍然是解向量,即可证明任意个解向量的常数倍之和(也就任意个解向量的线性组合)仍然是解向量
-
事实上,齐次线性方程组的全部解可以由有限个解向量(的线性组合)表示
基础解系
- 方程 ( 2 ) (2) (2)的所有解向量构成的向量集合(向量组)记为 S S S
- 设 S S S存在一个极大无关组 S 0 : ξ 1 , ⋯ , ξ t S_0:\xi_1,\cdots,\xi_t S0:ξ1,⋯,ξt,那么 S S S中的向量都能由 S 0 S_0 S0线性表示, S 0 S_0 S0称为 ( 2 ) (2) (2)的一个基础解系
通解
-
最大无关组 S 0 S_0 S0的任何线性组合 x = ∑ i = 1 r = k i ξ i \bold{x}=\sum_{i=1}^r=k_i\xi_{i} x=∑i=1r=kiξi,(, k i , i = 1 , 2 ⋯ , t k_i,i=1,2\cdots,t ki,i=1,2⋯,t为任意实数)是 ( 2 ) (2) (2)的解,能够表示 S S S中的任意向量,所有也成为 ( 2 ) (2) (2)的通解
-
把 A x = 0 Ax=0 Ax=0全体解所构成的集合记为 S S S,设 Φ = ξ 1 , ⋯ , ξ s \Phi=\xi_1,\cdots,\xi_s Φ=ξ1,⋯,ξs是S的一个极大无关组, R ( A ) = r , s = n − r R(A)=r,s=n-r R(A)=r,s=n−r
-
-
通解:最大无关组 Φ \Phi Φ的任意向量 x = Φ ( k 1 , ⋯ , k s ) T = ∑ i = 1 s k i ξ i x=\Phi(k_1,\cdots,k_s)^T=\sum\limits_{i=1}^{s}k_i\xi_i x=Φ(k1,⋯,ks)T=i=1∑skiξi性组合都是方程 A x = 0 Ax=0 Ax=0的解
- 通解(是 Φ \Phi Φ的生成子空间)
- 齐次线性方程组的通解可以描述(表出)方程组的任意一个解
-
齐次线性方程组 A x = 0 Ax=0 Ax=0的解集的极大无关组称为该齐次方程组的基础解系,要求齐次线性方程的通解,只需要求它的基础解系
定理:齐次线性方程组基础解系存在定理
- 若 R ( A ) = n R(A)=n R(A)=n,方程 ( 2 ) (2) (2)只有唯一解零解,不存在基础解系
- 若 R ( A ) < n R(A)<n R(A)<n,方程 ( 2 ) (2) (2)存在非零解(无穷多解),一定存在基础解系
齐次线性方程组的基础解系包含的向量个数(秩)👺
- 方程组解集的秩 R ( S ) R(S) R(S),即基础解系的秩的性质是十分有用的性质
- 揭示了方程(2)系数矩阵的秩 R ( A ) R(\bold{A}) R(A),解集的秩 R ( S ) R(S) R(S)与未知数(元)个数 n n n的关系
- 若方程(2)存在基础解系 A 0 A_0 A0,则包含的向量的个数为 n − r n-r n−r,即方程(2)的解集 S S S的秩为 R s = n − r R_s=n-r Rs=n−r,或者作 R ( A ) + R ( S ) = n R(A)+R(S)=n R(A)+R(S)=n
- 另一种描述:设 m × n m\times{n} m×n的矩阵 A \bold{A} A的秩为 R ( A ) = r R(\bold{A})=r R(A)=r,则 n n n元齐次线性方程组 A x = 0 \bold{Ax=0} Ax=0的解集 S S S的秩 R s = n − r R_{s}=n-r Rs=n−r
- 同时 n − r n-r n−r是方程(2)的通解中包含的自由未知数的个数;非自由未知数的个数则是系数矩阵的秩 r = R ( A ) r=R(\bold{A}) r=R(A)
应用和示例
推论1
- 设 A m × n B n × l = O \bold{A}_{m\times{n}}\bold{B}_{n\times{l}}=O Am×nBn×l=O,则 R ( A ) + R ( B ) ⩽ n R(\bold{A})+R(\bold{B})\leqslant{n} R(A)+R(B)⩽n
- 令 A = ( a 1 , ⋯ , a n ) \bold{A}=(\bold{a}_{1},\cdots,\bold{a}_{n}) A=(a1,⋯,an); B = ( b 1 , ⋯ , b l ) \bold{B}=(\bold{b}_{1},\cdots,\bold{b}_{l}) B=(b1,⋯,bl), A , B A,B A,B分别表示 A , B \bold{A,B} A,B列向量组
- 矩阵方程 A B = O \bold{AB=O} AB=O等价于向量方程组: A ( b 1 , ⋯ , b l ) = 0 \bold{A}(\bold{b}_{1},\cdots,\bold{b}_{l})=\bold{0} A(b1,⋯,bl)=0,即
- A b i = 0 \bold{A}\bold{b}_i=\bold{0} Abi=0, i = 1 , ⋯ , l i=1,\cdots,l i=1,⋯,l
- 可以看出 b i \bold{b}_i bi都是方程 A x = 0 \bold{Ax=0} Ax=0的解
- 设 A x = 0 \bold{Ax=0} Ax=0的解集为 S S S,则 b i ∈ S \bold{b}_i\in{S} bi∈S,说明 B B B是 S S S的部分组,所以 R ( B ) ⩽ R ( S ) R(B)\leqslant{R(S)} R(B)⩽R(S)
- 而 R ( S ) = n − R ( A ) R(S)=n-R(A) R(S)=n−R(A),所以 R ( B ) ⩽ n − R ( A ) R(B)\leqslant{n-R(A)} R(B)⩽n−R(A)
- 所以 R ( A ) + R ( B ) ⩽ n R(\bold{A})+R(\bold{B})\leqslant{n} R(A)+R(B)⩽n
推论2
- 设 n n n元齐次线性方程组 A x = 0 \bold{Ax=0} Ax=0与 B x = 0 \bold{Bx=0} Bx=0通解,则 R ( A ) R(\bold{A}) R(A)= R ( B ) R(\bold{B}) R(B)
- 分别设两个方程组的解集为 S 1 , S 2 S_1,S_2 S1,S2,则 S 1 = S 2 S_1=S_2 S1=S2
- 则 R ( A ) = n − R ( S 1 ) R(\bold A)=n-R(S_1) R(A)=n−R(S1); R ( B ) = n − R ( S 2 ) R(\bold B)=n-R(S_2) R(B)=n−R(S2)
- 又 R ( S 1 ) = R ( S 2 ) R(S_1)=R(S_2) R(S1)=R(S2),所以 R ( A ) R(\bold{A}) R(A)= R ( B ) R(\bold{B}) R(B)
- 这表明,当 A , B \bold{A,B} A,B的列数相同,(方程 A x = 0 , B x = 0 \bold{Ax=0},\bold{Bx=0} Ax=0,Bx=0包含数量相同的未知数)时
- 欲证 R ( A ) = R ( B ) R(\bold{A})=R(\bold{B}) R(A)=R(B),可以转换为证若 A x = 0 , B x = 0 \bold{Ax=0},\bold{Bx=0} Ax=0,Bx=0两个方程组同解
推论3:转置矩阵对的乘积秩的性质
- R ( A T A ) R(\bold{A^{T}{A}}) R(ATA)= R ( A ) R(\bold A) R(A)
- 证明:设 A \bold{A} A是 m × n m\times{n} m×n的令 B = A T A \bold{B=A^T{A}} B=ATA,显然 B \bold{B} B是 n × n n\times{n} n×n的
- 由此可见, A , B \bold{A,B} A,B有相同的列数
- 若 x \bold{x} x满足 A x = 0 \bold{Ax=0} Ax=0,则 A T ( A x ) = 0 \bold{A^T{(Ax)=0}} AT(Ax)=0也成立,由结合律: B x = 0 \bold{Bx=0} Bx=0
- 若 x \bold{x} x满足 B x = 0 \bold{Bx=0} Bx=0( n × 1 n\times{1} n×1),对其两边取转置运算, x T B T = 0 \bold{x^{T}B^{T}}=\bold{0} xTBT=0( 1 × n 1\times{n} 1×n),即 x T A T A = 0 \bold{x^{T}A^{T}A=0} xTATA=0( 1 × n 1\times{n} 1×n),再对两边同时右乘以 x \bold{x} x( n × 1 n\times{1} n×1),得 ( x T A T ) ( A x ) = 0 \bold{(x^{T}A^{T})(Ax)=0} (xTAT)(Ax)=0,即 ( A x ) T ( A x ) = 0 \bold{(Ax)^T(Ax)=0} (Ax)T(Ax)=0,由 X T X = O ⇒ X = O \bold{X^T{X}=O}\Rightarrow{\bold{X=O}} XTX=O⇒X=O可知, A x = 0 \bold{Ax=0} Ax=0
- 可见 A x = 0 , B x = 0 \bold{Ax=0},\bold{Bx=0} Ax=0,Bx=0同解,由推论2, R ( A ) = R ( B ) R(\bold{A})=R(\bold{B}) R(A)=R(B),所以结论成立
非自由未知数的选取方法(最左方法)
- 若方程 ( 2 ) (2) (2)的秩 R ( A ) = r < n R(A)=r<n R(A)=r<n,将前 r r r个未知数 x 1 , ⋯ , x r x_1,\cdots,x_r x1,⋯,xr作为非自由变量;其余 n − r n-r n−r个 x r + 1 , ⋯ , x n x_{r+1},\cdots,x_{n} xr+1,⋯,xn作为自由变量
- 种方式选择非自由变量和自由变量的方法是最常用的,称为最左方法
基础解系和通解形式的不唯一性
- 当 R ( A ) = r < n R(A)=r<n R(A)=r<n时,方程 ( 2 ) (2) (2)的基础解系包含 n − r n-r n−r个向量,因此任意 n − r n-r n−r个线性无关解向量都是 ( 2 ) (2) (2)的基础解系
- 即方程 ( 2 ) (2) (2)的基础解系不唯一,其通解形式也不唯一
证明
分析
-
方程 ( 2 ) (2) (2)的系数矩阵 A \bold{A} A通过初等变换(通解初等变换)可以得到如下形式的强化行最简形矩阵
-
B = ( 1 0 ⋯ 0 c 1 , 1 ⋯ c 1 , n − r 0 1 ⋯ 0 c 2 , 1 ⋯ c 2 , n − r ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 1 c r , 1 ⋯ c r , n − r 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 ⋯ 0 0 ⋯ 0 ) = ( E r C O O ) B=\begin{pmatrix} 1 & 0 & \cdots & 0 & c_{1,1} & \cdots & c_{1,n-r} \\ 0 & 1 & \cdots & 0 & c_{2,1} & \cdots & c_{2,n-r} \\ \vdots & \vdots & & \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & 1 & c_{r,1} & \cdots & c_{r,n-r}\\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & & \vdots & \vdots & & \vdots\\ 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \end{pmatrix} =\begin{pmatrix} E_r&C\\ O&O \end{pmatrix} B= 10⋮00⋮001⋮00⋮0⋯⋯⋯⋯⋯00⋮10⋮0c1,1c2,1⋮cr,10⋮0⋯⋯⋯⋯⋯c1,n−rc2,n−r⋮cr,n−r0⋮0 =(ErOCO)
-
按最左方法,其反映的是 x 1 , ⋯ , x r x_1,\cdots,x_r x1,⋯,xr是非自由未知数时, x r + 1 , ⋯ , x n x_{r+1},\cdots,x_{n} xr+1,⋯,xn是自由未知数(共 s = n − r s=n-r s=n−r个)
-
其中 s s s描述了方程组 ( 2 ) (2) (2)的自由度(基础解系包含的线性无关向量的多样性)
-
非自由未知数用自由未知数表示为式(1):
-
x i = − ∑ k = 1 s c i , k × x r + k ; ( i = 1 , 2 , ⋯ , r ) x_i=-\sum\limits_{k=1}^{s} c_{i,k}\times x_{r+k}; (i=1,2,\cdots,r) xi=−k=1∑sci,k×xr+k;(i=1,2,⋯,r)
-
ξ = ( x 1 ⋮ x r x r + 1 ⋮ x n ) = ( − ∑ i = 1 s c 1 , i × x r + i ⋮ − ∑ i = 1 s c r , i × x r + i x r + 1 ⋮ x n ) \xi=\begin{pmatrix} x_{1} \\ \vdots \\ x_{r} \\ x_{r+1} \\ \vdots \\ x_{n} \\ \end{pmatrix} =\begin{pmatrix} -\sum\limits_{i=1}^{s} c_{1,i}\times x_{r+i} \\ \vdots \\ -\sum\limits_{i=1}^{s} c_{r,i}\times x_{r+i} \\ x_{r+1} \\ \vdots \\ x_{n} \\ \end{pmatrix} ξ= x1⋮xrxr+1⋮xn = −i=1∑sc1,i×xr+i⋮−i=1∑scr,i×xr+ixr+1⋮xn
-
-
设方程 ( 2 ) (2) (2)的全部解的集合为 S S S
-
证法1
齐次线性方程的基础解系构造
-
( 2 ) (2) (2)的解是 n n n维向量,分两部分,前 r r r为非自由未知数,后 s s s维为自由未知数
-
设计特解时,先选定后 s s s维
-
为了简单方便起见,通常取解向量的后s维为单位坐标向量(向量中只含有一个0,1两种元素,且只有一个元素是1)
-
q i = ( x r + 1 ⋮ x n ) q 1 = ( 1 0 ⋮ 0 ) ; q 2 = ( 0 1 ⋮ 0 ) ; ⋯ ; q s = ( 0 0 ⋮ 1 ) q_i=\begin{pmatrix} x_{r+1} \\ \vdots \\ x_{n} \\ \end{pmatrix} \\ q_1=\begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \\ \end{pmatrix}; q_2=\begin{pmatrix} 0 \\ 1 \\ \vdots \\ 0 \\ \end{pmatrix}; \cdots; q_s=\begin{pmatrix} 0 \\ 0\\ \vdots \\ 1 \\ \end{pmatrix} qi= xr+1⋮xn q1= 10⋮0 ;q2= 01⋮0 ;⋯;qs= 00⋮1
-
-
计算前 r r r维(将 q i , i = 1 , 2 , ⋯ , s q_i,i=1,2,\cdots,s qi,i=1,2,⋯,s代入式(1))
-
p i = ( x 1 ⋮ x r ) p_i=\begin{pmatrix} x_{1} \\ \vdots \\ x_{r} \\ \end{pmatrix} pi= x1⋮xr
-
p 1 = ( − c 1 , 1 − c 2 , 1 ⋯ − c r , 1 ) ; p 2 = ( − c 1 , 2 − c 2 , 2 ⋯ − c r , 2 ) ; ⋯ ; p s = ( − c 1 , n − r − c 2 , n − r ⋯ − c r , n − r ) p_1=\begin{pmatrix} -c_{1,1}\\ -c_{2,1}\\ \cdots\\ -c_{r,1} \end{pmatrix}; p_2=\begin{pmatrix} -c_{1,2}\\ -c_{2,2}\\ \cdots\\ -c_{r,2} \end{pmatrix}; \cdots; p_s=\begin{pmatrix} -c_{1,n-r}\\ -c_{2,n-r}\\ \cdots\\ -c_{r,n-r} \end{pmatrix} p1= −c1,1−c2,1⋯−cr,1 ;p2= −c1,2−c2,2⋯−cr,2 ;⋯;ps= −c1,n−r−c2,n−r⋯−cr,n−r
-
-
ξ = ( p q ) \xi=\begin{pmatrix} p\\q \end{pmatrix} ξ=(pq)
ξ 1 = ( − c 1 , 1 − c 2 , 1 ⋯ − c r , 1 1 0 ⋮ 0 ) ; ξ 2 = ( − c 1 , 2 − c 2 , 2 ⋯ − c r , 2 0 1 ⋮ 0 ) ; ⋯ ; ξ s = ( − c 1 , n − r − c 2 , n − r ⋯ − c r , n − r 0 0 ⋮ 1 ) ; \xi_1=\begin{pmatrix} -c_{1,1}\\ -c_{2,1}\\ \cdots\\ -c_{r,1}\\ 1 \\ 0 \\ \vdots \\ 0 \\ \end{pmatrix}; \xi_2=\begin{pmatrix} -c_{1,2}\\ -c_{2,2}\\ \cdots\\ -c_{r,2} \\ 0\\ 1 \\ \vdots \\ 0 \\ \end{pmatrix}; \cdots; \xi_s=\begin{pmatrix} -c_{1,n-r}\\ -c_{2,n-r}\\ \cdots\\ -c_{r,n-r}\\ 0 \\ 0 \\ \vdots \\ 1 \\ \end{pmatrix}; ξ1= −c1,1−c2,1⋯−cr,110⋮0 ;ξ2= −c1,2−c2,2⋯−cr,201⋮0 ;⋯;ξs= −c1,n−r−c2,n−r⋯−cr,n−r00⋮1 ;
-
证明所构造的向量组是基础解系
-
线性无关性:
- 方法1:矩阵 D = ( ξ 1 , ⋯ , ξ s ) \bold{D}=(\xi_1,\cdots,\xi_{s}) D=(ξ1,⋯,ξs)中包含 E s \bold{E}_{s} Es,且 ∣ E n − r ∣ = s ≠ 0 |\bold{E}_{n-r}|=s\neq{0} ∣En−r∣=s=0, R ( D ) = s R(\bold{D})=s R(D)=s所以 D : ξ 1 , ⋯ , ξ s {D}:\xi_1,\cdots,\xi_{s} D:ξ1,⋯,ξs线性无关
- 方法2:由 ξ i \xi_i ξi的结构可以看出, ξ i \xi_i ξi的后s维是构成的向量之间是线性无关的,而线性无关组的延伸组依然线性无关
-
S S S的全部向量可以由 D D D线性表示:
- 设向量 ξ = ( k 1 , ⋯ , k r , k r + 1 , ⋯ , k n ) \xi=(k_1,\cdots,k_r,k_{r+1},\cdots,k_n) ξ=(k1,⋯,kr,kr+1,⋯,kn)是 S S S的任意一个向量,
- 构造向量 D D D的线性组合: ξ ∗ = ∑ i = 1 s k r + i ξ i \xi^*=\sum\limits_{i=1}^{s}k_{r+i}\xi_i ξ∗=i=1∑skr+iξi则 ξ ∗ \xi^* ξ∗也是方程 ( 2 ) (2) (2)的通解,并且表出系数来自需要被 D D D线性表示的向量 ξ \xi ξ的第 r + 1 , ⋯ , n r+1,\cdots,n r+1,⋯,n个元
- 容易发现, ξ ∗ \xi^{*} ξ∗和 ξ \xi ξ在第 r + 1 , ⋯ , n r+1,\cdots,n r+1,⋯,n维是相同的
- 又根据前面的分析以及式(1),方程 ( 2 ) (2) (2)的解向量包括非自由变量和自由变量,其中非自由变量取决于自由变量的取值,所以非自由变量完全确定了整个解向量(若两个解向量的非自由未知数一样,则两个解向量相等)
- 所以 ξ ∗ = ξ \xi^*=\xi ξ∗=ξ,即任意解向量都能由 ξ ∗ \xi^* ξ∗(即 D D D的线性组合)表示
- 所以 S S S的全部向量可以由 D D D线性表示
- 设向量 ξ = ( k 1 , ⋯ , k r , k r + 1 , ⋯ , k n ) \xi=(k_1,\cdots,k_r,k_{r+1},\cdots,k_n) ξ=(k1,⋯,kr,kr+1,⋯,kn)是 S S S的任意一个向量,
-
所以 D D D是 S S S的极大无关组,所以 D D D方程 ( 2 ) (2) (2)的基础解系
证法2
-
令自由未知量 x r + i x_{r+i} xr+i分别取 k i k_i ki, i = 1 , 2 , ⋯ , s i=1,2,\cdots,s i=1,2,⋯,s;代入式 ( 1 ) (1) (1);则方程 ( 2 ) (2) (2)的通解表示为
ξ = ( x 1 ⋮ x r x r + 1 ⋮ x n ) = ( x 1 ⋮ x r k 1 ⋮ k s ) = ( − ∑ i = 1 s c 1 , i × k i ⋮ − ∑ i = 1 s c r , i × k i k 1 ⋮ k s ) = k 1 ( − c 1 , 1 ⋮ − c r , 1 1 ⋮ 0 ) + ⋯ + k s ( − c 1 , s ⋮ − c r , s 0 ⋮ 1 ) \xi=\begin{pmatrix} x_{1} \\ \vdots \\ x_{r} \\ x_{r+1} \\ \vdots \\ x_{n} \\ \end{pmatrix} =\begin{pmatrix} x_{1} \\ \vdots \\ x_{r} \\ k_{1} \\ \vdots \\ k_{s} \\ \end{pmatrix} =\begin{pmatrix} -\sum\limits_{i=1}^{s} c_{1,i}\times k_{i} \\ \vdots \\ -\sum\limits_{i=1}^{s} c_{r,i}\times k_{i} \\ k_{1} \\ \vdots \\ k_{s} \\ \end{pmatrix} =k_1\begin{pmatrix} -c_{1,1} \\ \vdots \\ -c_{r,1} \\ 1 \\ \vdots \\ 0 \\ \end{pmatrix} +\cdots +k_s\begin{pmatrix} -c_{1,s} \\ \vdots \\ -c_{r,s} \\ 0 \\ \vdots \\ 1 \\ \end{pmatrix} ξ= x1⋮xrxr+1⋮xn = x1⋮xrk1⋮ks = −i=1∑sc1,i×ki⋮−i=1∑scr,i×kik1⋮ks =k1 −c1,1⋮−cr,11⋮0 +⋯+ks −c1,s⋮−cr,s0⋮1 -
将上述通解记为: ξ = ∑ i = 1 s k i ξ i \xi=\sum_{i=1}^{s}k_i\xi_i ξ=∑i=1skiξi,涉及的向量记为向量组: D = ( ξ 1 , ⋯ , ξ s ) \bold{D}=(\xi_1,\cdots,\xi_{s}) D=(ξ1,⋯,ξs)
-
通解 ξ \xi ξ可以表示 S S S中的任意向量
-
而 D D D中后 s s s行构成一个 s s s阶单位阵,其行列式为1(非0),所以 R ( D ) = s R(D)=s R(D)=s所以 D D D线性无关
-
所以 D D D是方程 ( 2 ) (2) (2)的一个基础解系解系
小结
- 上述两种方法一种是先求基础解系再求通解;另一种是先求通解再求基础解系
基础解系构造提要
-
可以从 A x = 0 Ax=0 Ax=0的系数矩阵A通过初等变换转化为(包含r阶单位子阵,r=R(A))的强化行最简矩阵U,
-
r = R ( A ) , s = n − r r=R(A),s=n-r r=R(A),s=n−r
-
U = ( E r × r T r × s 0 t × r 0 t × s ) r + s = n D = ( − T r × s E s × s ) U=\begin{pmatrix} E_{r\times{r}}&T_{r\times{s}}\\ 0_{t\times{r}}&0_{t\times{s}} \end{pmatrix} \\ r+s=n \\ \bold{D}=\begin{pmatrix} -T_{r\times{s}} \\ E_{s\times{s}} \end{pmatrix} U=(Er×r0t×rTr×s0t×s)r+s=nD=(−Tr×sEs×s)
-
D : ξ 1 , ξ 2 , ⋯ , ξ s D:\xi_1,\xi_2,\cdots,\xi_s D:ξ1,ξ2,⋯,ξs是 D \bold{D} D的列向量组
-
D D D就是 A x = 0 \bold{Ax=0} Ax=0的基础解系
-
-
我们把注意力集中在分块 P r × s = − T r × s P_{r\times{s}}=-T_{r\times{s}} Pr×s=−Tr×s上即可,在此基础上,追加一个s阶的单位阵;
- 最终该矩阵的每个列向量就是基础解系的一个解向量成员
-
-
方法1:不一定要化作强化行最简形矩阵,也可以考虑化为准行最简形矩阵(W)(和强化行最简形矩阵相差若干列交换的调整)
- 从 W W W中读出 r r r个非自由未知数用 n − r n-r n−r个自由未知数的表达式
- 取定合适的 n − r n-r n−r个组值(每组值可以来自 n − r n-r n−r阶单位阵的不同列),得到 n − r n-r n−r个解向量作为基础解系
- 得到通解
-
方法2:将行简化矩阵进一步调整为 U U U的形式可能要做列交换,这会使得解向量中的元素不再和 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn一一对应,需要注意这一点,记录列交换的情况,然后调整顺序使之对应 x 1 , ⋯ , x n x_1,\cdots,x_n x1,⋯,xn
例
-
设 A x = 0 \bold{Ax=0} Ax=0:
-
A = ( 1 1 − 1 − 1 2 − 5 3 2 7 − 7 3 1 ) ∼ r ( 1 0 − 2 7 − 3 7 0 1 − 5 7 − 4 7 0 0 0 0 ) \bold{A} =\begin{pmatrix} 1&1&-1&-1\\ 2&-5&3&2\\ 7&-7&3&1 \end{pmatrix} \overset{r}{\sim} \begin{pmatrix} 1&0&-\frac{2}{7}&-\frac{3}{7}\\ 0&1&-\frac{5}{7}&-\frac{4}{7}\\ 0&0&0&0 \end{pmatrix} A= 1271−5−7−133−121 ∼r 100010−72−750−73−740
-
R ( A ) = 2 < 4 R(A)=2<4 R(A)=2<4方程有无穷多解,其基础解系 S 0 S_0 S0存在且 R ( S 0 ) = n − r = 4 − 2 = 2 R(S_0)=n-r=4-2=2 R(S0)=n−r=4−2=2
-
令 x 1 , x 2 x_1,x_2 x1,x2为非自由未知数, x 3 , x 4 x_3,x_4 x3,x4为自由未知数
-
x 1 = 2 7 x 3 + 3 4 x 4 x 2 = 5 7 x 3 + 4 7 x 4 x_1=\frac{2}{7}x_3+\frac{3}{4}x_4\\ x_2=\frac{5}{7}x_3+\frac{4}{7}x_4 x1=72x3+43x4x2=75x3+74x4
-
-
基础解系
- 令取2组自由未知数的取值: q 1 q_1 q1= ( 1 0 ) \begin{pmatrix}1\\0\end{pmatrix} (10), q 2 q_2 q2= ( 0 1 ) \begin{pmatrix}0\\1\end{pmatrix} (01),则对应的非自由未知数向量: p 1 p_1 p1= ( 2 7 5 7 ) \begin{pmatrix}\frac{2}{7}\\\frac{5}{7}\end{pmatrix} (7275), q 2 q_2 q2= ( 3 7 4 7 ) \begin{pmatrix}\frac{3}{7}\\\frac{4}{7}\end{pmatrix} (7374)
- 即得方程组得解集中的两个线性无关的特解 ξ 1 = ( 2 7 5 7 1 0 ) \xi_1=\begin{pmatrix}\frac{2}{7}\\\frac{5}{7}\\1\\0\end{pmatrix} ξ1= 727510 ; ξ 2 = ( 3 7 4 7 0 1 ) \xi_2=\begin{pmatrix}\frac{3}{7}\\\frac{4}{7}\\0\\1\end{pmatrix} ξ2= 737401
- (Note:如果用构造提要一节中,可以直接得出 ξ 1 , ξ 2 \xi_1,\xi_2 ξ1,ξ2)
-
通解
- ξ = ∑ i = 1 2 k i ξ i \xi=\sum_{i=1}^{2}k_i\xi_i ξ=∑i=12kiξi,其中 k i ∈ R k_i\in\mathbb{R} ki∈R
补充
- 结合上面的例子讨论
再给出一组上述基础解系之外的其他基础解系
- 例如
- q 1 q_1 q1= ( 1 1 ) \begin{pmatrix}1\\1\end{pmatrix} (11), q 2 q_2 q2= ( 1 − 1 ) \begin{pmatrix}1\\-1\end{pmatrix} (1−1), q 1 , q 2 q_1,q_2 q1,q2线性无关(不成比例)
- η 1 = ( 5 7 7 9 1 1 ) \eta_1=\begin{pmatrix}\frac{5}{7}\\\frac{7}{9}\\1\\1\end{pmatrix} η1= 759711 ; η 2 = ( − 1 7 1 7 1 − 1 ) \eta_2=\begin{pmatrix}-\frac{1}{7}\\\frac{1}{7}\\1\\-1\end{pmatrix} η2= −71711−1
- 则 η 1 , η 2 \eta_1,\eta_2 η1,η2与 ξ 1 , ξ 2 \xi_1,\xi_2 ξ1,ξ2同为 S S S的极大无关组,都是方程组的基础解系
非最左方法选取非自由变量
-
非自由变量的选取不按最左方法时,求解基础解系的过程相较于上节讨论的"标准过程"会有所不同
-
例如 x 1 x_1 x1若按最左方法会被归为非自由未知数,但是这假设 x 1 x_1 x1被作为自由未知数
- 相应的,需要有其他未知数 x j , j ≠ 1 x_j,j\neq{1} xj,j=1代替原 x 1 x_1 x1作为非自由未知数
- 在标准过程中,行最简形矩阵的第1列是 e 1 = ( 1 , 0 , ⋯ , 0 ) T \bold{e}_1=(1,0,\cdots,0)^T e1=(1,0,⋯,0)T
- 在这里利用行变换,将 A \bold{A} A的第 j j j列(记为 c j c_j cj,是 x j x_j xj的系数, j ≠ 1 j\neq{1} j=1)变换成 e 1 \bold{e}_1 e1
- 类似的,共可以选出 n − r n-r n−r个自由未知数设为 x j k x_{j_k} xjk, ( k = 1 , ⋯ , n − r ) (k=1,\cdots,n-r) (k=1,⋯,n−r),需要通过初等行变换,将 A \bold{A} A中的其他 r r r个非自由未知数分别转换为 e i \bold{e}_{i} ei( e i \bold{e}_{i} ei表示 n n n维单位坐标向量中第 i i i维是1的列向量, j k j_k jk之间互不相等)
- 此时的矩阵虽然不是行最简形矩阵,(这类矩阵不是唯一的),其具有和行最简形矩阵相同的作用,称其为准行最简形矩阵都能够利用 r r r个 n n n维单位坐标向量读出 n − r n-r n−r个自由未知数表示 r r r个非自由未知数的表出系数
-
本例中,我们打算将 x 1 , x 2 x_1,x_2 x1,x2作为自由未知数来表示非自由未知数 x 3 , x 4 x_3,x_4 x3,x4,
-
A = ( 1 1 − 1 − 1 2 − 5 3 2 7 − 7 3 1 ) ∼ r ( − 5 2 0 1 4 − 3 1 0 0 0 0 0 ) \bold{A} =\begin{pmatrix} 1&1&-1&-1\\ 2&-5&3&2\\ 7&-7&3&1 \end{pmatrix} \overset{r}{\sim} \begin{pmatrix} -5&2&0&1\\ 4&-3&1&0\\ 0&0&0&0 \end{pmatrix} A= 1271−5−7−133−121 ∼r −5402−30010100
-
类似的,可以看出 x 3 = − 4 x 1 + 3 x 2 x_3=-4x_1+3x_2 x3=−4x1+3x2; x 4 = 5 x 1 − 2 x 2 x_4=5x_1-2x_2 x4=5x1−2x2, x 1 , x 2 ∈ R x_1,x_2\in\mathbb{R} x1,x2∈R
-
此时基础解系可以取
-
ξ 1 = ( 1 0 − 4 5 ) ; ξ 2 = ( 0 1 3 − 2 ) \xi_1=\begin{pmatrix} 1\\0\\-4\\5 \end{pmatrix}; \xi_2=\begin{pmatrix} 0\\1\\3\\-2 \end{pmatrix} ξ1= 10−45 ;ξ2= 013−2
-
通解为 ξ = ∑ i = 1 2 k i ξ i \xi=\sum_{i=1}^{2}k_i\xi_i ξ=∑i=12kiξi
-
-
-
相关文章:

LA@齐次线性方程组解的结构
文章目录 齐次线性方程组解的结构🎈解的性质齐次线性方程组的解的线性组合还是方程组的解基础解系通解 定理:齐次线性方程组基础解系存在定理齐次线性方程组的基础解系包含的向量个数(秩)👺应用和示例推论1推论2推论3:转置矩阵对的乘积秩的性质非自由未知…...

Docker修改容器ulimit的全部方案及各方案的详细步骤
要修改Docker容器的ulimit(用户资源限制),有以下三种方案,每个方案的详细步骤如下: 方案一:在Dockerfile中设置ulimit 打开您的Dockerfile。在文件中添加以下命令来修改ulimit:RUN ulimit -n …...
进程间通信-Binder
Binder Binder框架概述服务端Binder驱动客户端 设计服务端和客户端设计服务端客户端设计 Binder与ServiceServiceAIDL 保证包裹内参数顺序IMusicPlayerServiceProxyStub 系统服务中的Binder对象ServiceManger管理的服务理解Manger功能快捷键合理的创建标题,有助于目…...

一个简单的vim例子
一.欢迎来到我的酒馆 在本章节介绍vim工具。 目录 一.欢迎来到我的酒馆二.什么是vim三.开始使用vim 二.什么是vim 2.1什么是vim vim是一种Linux命令行类型的文本编辑器。vim指的是"vi improved",意思是vi工具的升级版。vim是基于vi实现的&#x…...
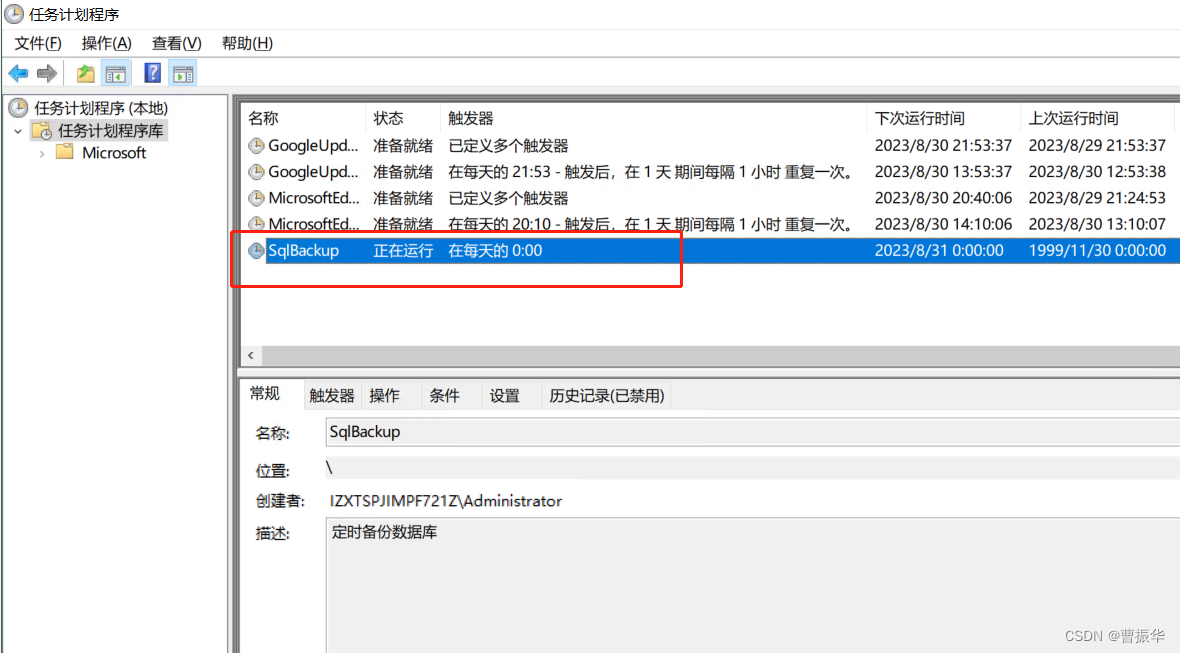
sql server 备份到网络共享
场景:sql server服务器A将数据库备份文件备份到服务器B 1)服务器B创建共享目录 这里我将 D:\ProDbBak 共享,并且Everyone完全控制 2)sql server服务器A能够访问服务器B共享目录,并且能完全控制 3)修改服务…...

程序与进程
一、程序是怎么被执行的 1.在程序中,由引导代码去调用程序中得main函数,而这个过程由链接器完成,链接器将引导代码链接到我们的应用程序构成可执行文件。 2.程序运行需要通过操作系统的加载器来实现,加载器是操作系统中的程序&a…...
-[链与索引:图问答(Graph QA)和带来源的问答(QA with Sources)])
大模型从入门到应用——LangChain:链(Chains)-[链与索引:图问答(Graph QA)和带来源的问答(QA with Sources)]
分类目录:《大模型从入门到应用》总目录 图问答(Graph QA) 创建图 在本节中,我们构建一个示例图。目前,这对于较小的文本片段效果最好,下面的示例中我们只使用一个小片段,因为提取知识三元组对…...

spark sql 数据倾斜--join 同时开窗去重的问题优化
spark sql 数据倾斜–join 同时开窗去重的问题优化 文章目录 spark sql 数据倾斜--join 同时开窗去重的问题优化结论1. 原方案:join步骤时,同时开窗去重数据倾斜 2. 优化2.1 参数调优2.2 SQL优化 背景: 需求:在一张查询日志表中&a…...
lv3 嵌入式开发-linux介绍及环境配置
目录 1 UNIX、Linux和GNU简介 2 环境介绍 3 VMwareTools配置 4 vim配置: 1 UNIX、Linux和GNU简介 什么是UNIX? unix是一个强大的多用户、多任务操作系统,支持多种处理器架构 中文名 尤尼斯 外文名 UNIX 本质 操作系统 类型 分时操作系统 开…...

RabbitMQ工作模式-路由模式
官方文档参考:https://www.rabbitmq.com/tutorials/tutorial-four-python.html 使用direct类型的Exchange,发N条消息并使用不同的routingKey,消费者定义队列并将队列routingKey、Exchange绑定。此时使用direct模式Exchange必须要routingKey完成匹配的情况下消息才…...

StringIO BytesIO
上一篇中我们介绍了文件的基本读写操作,但是很多时候数据的读写并不一定都是在文件中,我们也可以在内存中读写数据,因此引出我们今天的主要内容,即 StringIO 和 BytesIO,让你学会在内存中进行数据的基本读写操作。 1 …...

通讯录管理系统(个人学习笔记黑马学习)
1、系统需求 通讯录是一个可以记录亲人、好友信息的工具。 本教程主要利用C来实现一个通讯录管理系统系统中需要实现的功能如下: 添加联系人:向通讯录中添加新人,信息包括(姓名、性别、年龄、联系电话、家庭住址)最多记录1000人显示联系人:显示通讯录中所有联系人信…...
[SpringBoot3]远程访问@HttpExchange
六、远程访问HttpExchange[SpringBoot3] 远程访问是开发的常用技术,一个应用能够访问其他应用的功能。SpringBoot提供了多种远程访问的技术。基于HTTP协议的远程访问是最广泛的。SpringBoot中定义接口提供HTTP服务。生成的代理对象实现此接口,代理对象实…...

Linux安装ntp并使用阿里云配置ntp服务器
安装 NTP 客户端: 打开终端,以 root 权限执行以下命令来安装 NTP 客户端: sudo zypper install ntp 编辑 NTP 配置文件: 使用文本编辑器打开 NTP 的配置文件 /etc/ntp.conf,例如使用 nano 编辑器: sudo v…...

js常用方法总结
1、slice 和 splice slice表示截取,slice(start,end),不改变原数组,返回新数组。 splice表示删除,splice(start,length,item),会改变原数组,从某个位置开始删除多个元素,并可以插入新的元素。…...

在PHP中安装Composer并管理Vue前端依赖包
系列文章目录 文章目录 系列文章目录前言一、安装Composer二、使用Composer管理PHP依赖包三、使用npm管理Vue前端依赖包总结 前言 在开发Web应用程序时,使用Composer来管理PHP的依赖包和Vue前端的依赖包是一种很常见的做法。Composer是PHP的包管理工具,…...

03-前端基础CSS-第一天
01-CSS层叠样式表导读 目标: 能够说出什么是CSS能够使用CSS基础选择器能够设置字体样式能够设置文本样式能够说出CSS的三种引入方式能够使用Chrome调试工具调试样式 目录: 1.CSS简介2.CSS基础选择器3.CSS字体属性4.CSS文本属性5.CSS引入方式6.综合案…...
多张图片转为pdf怎么弄?
多张图片转为pdf怎么弄?在网络传输过程中,为了避免图片格式文件出现差错,并确保图片的清晰度和色彩不因不同设备而有所改变,常见的做法是将图片转换为PDF格式。然而,当涉及到多张图片时,逐一转换将会变得相…...

jdk新版本特性
JDK8,JDK11,JDK17,JDK21及中间版本主要更新特性_jdk重要版本_ycsdn10的博客-CSDN博客 Java 20 新特性概览 | JavaGuide(Java面试 学习指南)...
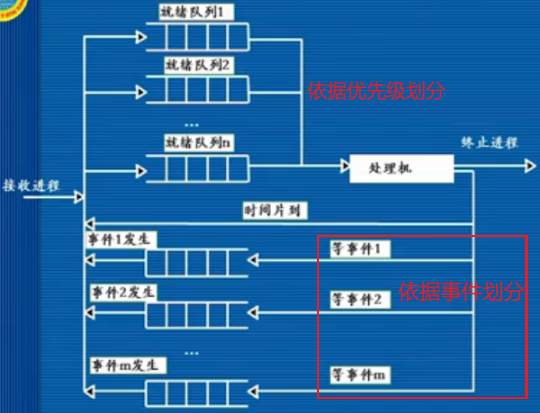
进程Start
Linux中的命令解释器和Windows的程序管理器explorer.exe一样地位,都是在用户态下运行的进程 共享变量发生不同进程间的指令交错,就可能会数据出错 进程只作为除CPU之外系统资源的分配单位 CPU的分配单位是线程 每个进程都有自己的独立用户空间 内核空间是OS内核的…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
