xss基础
目录标题
- 一、XSS的原理
- 二、XSS漏洞分类
- 1、反射型xss
- 2、存储型XSS
- 3、基于DOM的XSS
- 三、XSS漏洞的危害及验证
- 四、XSS漏洞的黑盒测试
- 五、XSS漏洞的白盒测试
一、XSS的原理
跨站脚本攻击XSS(Cross Site Scripting),为了不和层叠样式表(Cascading Style Sheets,CSS)的缩写混淆,故将跨站脚本攻击缩写为XSS。恶意攻击者往Web页面里插入恶意Script代码,当用户浏览该页时,嵌入其中Web里面的Script代码会被执行,从而达到恶意攻击用户的目的。XSS攻击针对的是用户层面的攻击!
二、XSS漏洞分类
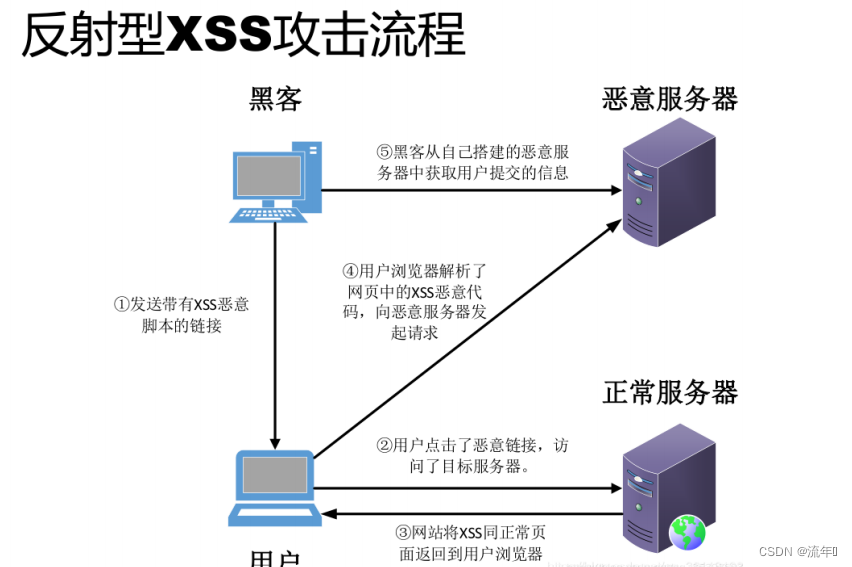
1、反射型xss
反射型XSS是非持久性、参数型的跨站脚本。反射性XSS的JS代码在Web应用的参数(变量)中,如搜索框中,提交PoC[scriptalert(/xss/)/script],单击搜索,即可触发反射型XSS。这时就会注意到,我们提交的poc会出现在search.php页面的keywords参数中。
2、存储型XSS
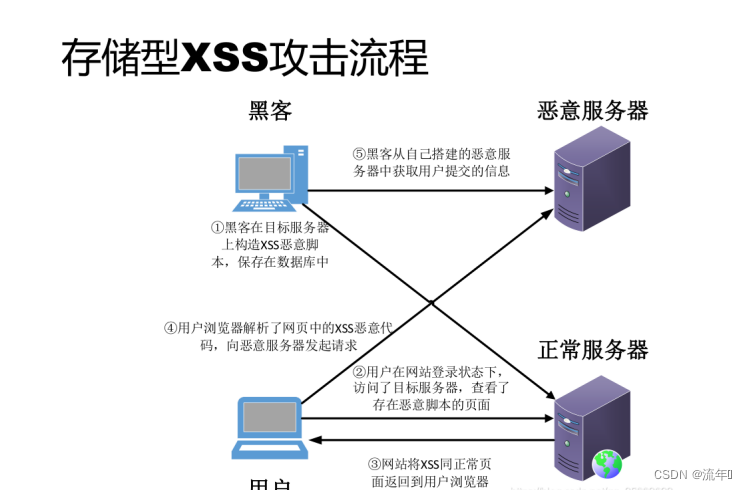
存储型XSS是持久性跨站脚本。持久性体现在XSS代码不是在某个参数(变量)中,而是写进数据库或文件等可以永久保存数据的介质中。存储型XSS通常发生在留言板等地方。我们在留言板位置留言,将恶意代码写进数据中。此时,我们只完成了第一步,将恶意代码写入数据库。因为XSS是的JS代码,JS代码运行的环境是浏览器,所以需要浏览器从服务器载入恶意的XSS代码,才能真正触发XSS。此时,需要我们模拟网站后台管理员的身份,查看留言。
3、基于DOM的XSS
DOM的XSS比较特殊。owasp关于DOM型号XSS的定义是基于DOM的XSS是一种XSS攻击,其中攻击的payload由于修改受害者浏览器页面的DOM树而执行的。其特殊的地方就是payload在浏览器本地修改DOM树而执行,并不会传到服务器上,这也就使得DOM XSS比较难以检测。
三、XSS漏洞的危害及验证
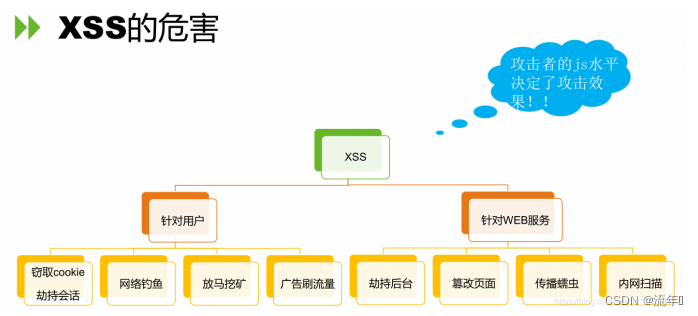
我们可以使用一段简单代码,验证和检测漏洞的存在,这样的代码叫做PoC(Proof of Concept)。验证XSS漏洞存在的PoC如下:
(1)scriptalert(/xss/)/script
(2)scriptconfirm('xss')/script
(3)scriptprompt('xss')/script
四、XSS漏洞的黑盒测试
尽可能找到一切用户可控并且能够输出在页面代码中的地方,比如下面这些:
URL的每一个参数、URL本身、表单、搜索框、常见业务场景
重灾区:评论区、留言区、个人信息、订单信息等
针对性:站内信、网页即时通讯、私信、意见反馈
存在风险:搜索框、当前目录、图片属性等
五、XSS漏洞的白盒测试
关于XSS的代码审计主要就是从接收参数的地方和一些关键词入手。
PHP中常见的接收参数的方式有$GET、$POST、$_REQUEST等等,可以搜索所有接收参数的地方。然后对接收到的数据进行跟踪,看看有没有输出到页面中,然后看输出到页面中的数据是否进行了过滤和html编码等处理。
也可以搜索类似echo这样的输出语句,跟踪输出的变量是从哪里来的,我们是否能控制,如果从数据库中取的,是否能控制存到数据库中的数据,存到数据库之前有没有进行过滤等等。
大多数程序会对接收参数封装在公共文件的函数中统一调用,我们就需要审计这些公共函数看有没有过滤,能否绕过等等
相关文章:

xss基础
目录标题一、XSS的原理二、XSS漏洞分类1、反射型xss2、存储型XSS3、基于DOM的XSS三、XSS漏洞的危害及验证四、XSS漏洞的黑盒测试五、XSS漏洞的白盒测试一、XSS的原理 跨站脚本攻击XSS(Cross Site Scripting),为了不和层叠样式表(…...
移动WEB开发二、流式布局
零、文章目录 文章地址 个人博客-CSDN地址:https://blog.csdn.net/liyou123456789个人博客-GiteePages:https://bluecusliyou.gitee.io/techlearn 代码仓库地址 Gitee:https://gitee.com/bluecusliyou/TechLearnGithub:https:…...

分享在线预约系统制作步骤_在线预约链接怎么做
在微信小程序上进行在线预约,不管是商家还是顾客,都可以自由选择时间,顾客还可以通过预约小程序,了解到所选服务的详情和功能特色,不必等到去店内听介绍,顾客能节省等候时间,商家能解放招待人力…...

【每日一题Day125】LC1326灌溉花园的最少水龙头数目 | 动态规划 贪心
灌溉花园的最少水龙头数目【LC1326】 在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。 花园里总共有 n 1 个水龙头,分别位于 [0, 1, ..., n] 。 给你一个整数 n 和一个长度为 n 1 的整数数组 ranges ,其中 …...
C# FFmpeg推流Vlc.DotNet拉流优化参数
FFmpeg是流媒体开源神器,视频转换、剪裁包括推流,无所不能,很多系统都是基于其开发的。拉流可以用FFplay,但是不利于集成到自己的代码中,因此拉流选择了Vlc.DotNet。 在使用中,仅使用默认参数,…...
)
pnpm v8版本升级变化关注点(前瞻速攻版)
前言 pnpm v8.0.0-alpha.0 版本已经发布,包含少量变化,但其中还是有令人在意的点的。 本文将默认读者拥有大部分 pnpm v7 版本的知识储备,进行 v8 版本的前瞻速攻。 安装方法 目前通过指定 Tag 方式可以安装 v8 alpha 版: npm…...
Python基础-环境安装
Python安装1.下载PythonPython网址:https://www.python.org/进入Python官网,点击Downloads,选择自己对应的操作系统(此处以Windows为例)在左侧的稳定发行版中,选择一个3.5版本以上的,然后点击对…...

重载、重写、重构概念辨析
首先,重载、重写、重构都表现为方法名相同 重载 重载(overload),表示同一类的方法之间的关系,至少有以下其中一种情况 参数个数不同参数类型不同参数顺序不同 注意,返回值类型不同不能作为重载依据 重…...
第九章 - 多表查询(join,left join 等)与合并查询(union union all)
第九章 - 多表查询(join,left join 等)与合并查询(union)交叉链接(笛卡尔积)内连接查询外连接查询左链接: left join右链接:right join组合查询 union & union all使…...
matplotlib学习笔记(持续更新中…)
目录 1. 安装,导入 2. figure,axes(图形,坐标图形) 2.1 figure对象 2.2 axes对象 2.3 代码演示 2.3 subplot() 方法 3. 图表的导出 3.1 savefig() 方法 3.2 代码演示 1. 安装,导入 pip install m…...
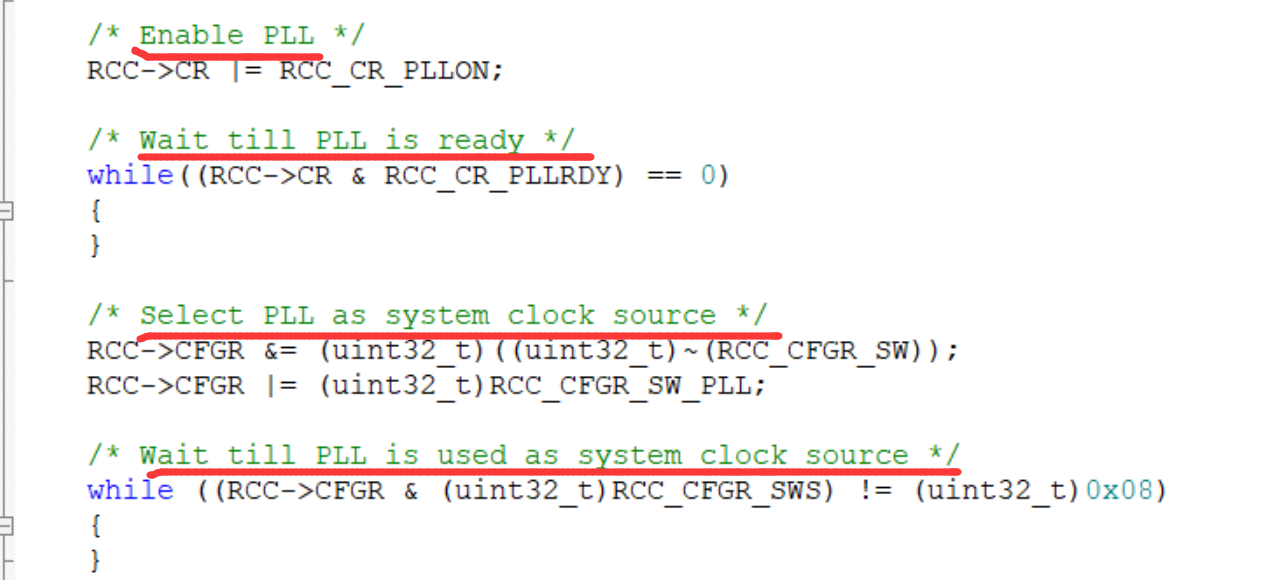
STM32 SystemInit()函数学习总结
拿到程序后如何看系统时钟?User文件夹——system_stm32f4xx程序,先找systemcoreclock(系统时钟)但是这里这么多个系统时钟应该如何选择?点击魔法棒,然后点击C/C可以看到define的是F40_41XXX.USE这一款 ,对应着就找出了…...
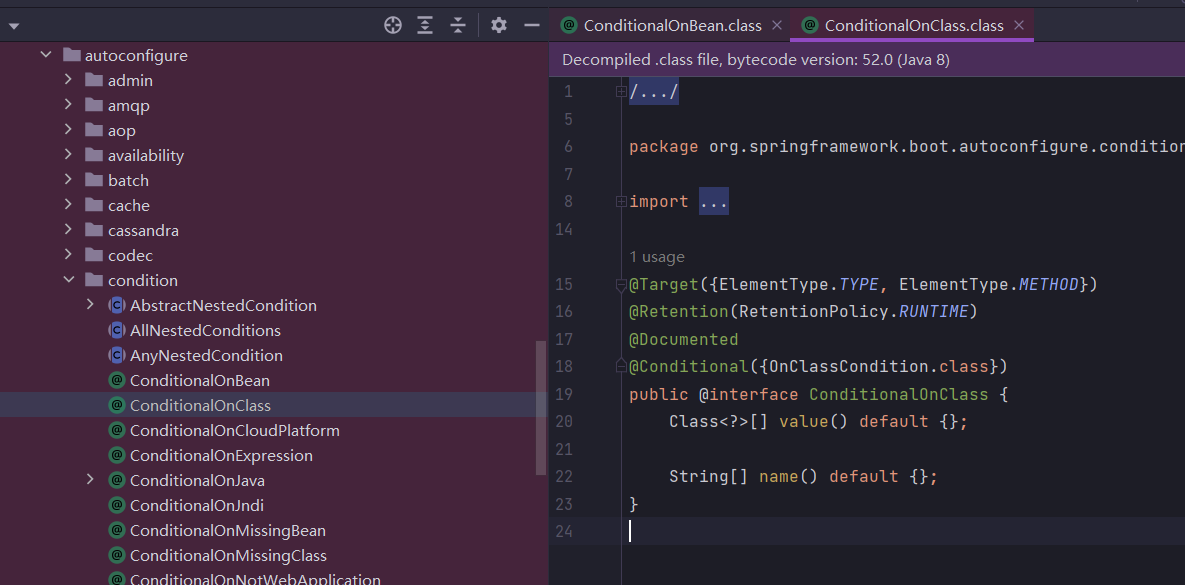
【Spring Boot 原理分析】- 自动配置
【Spring Boot 原理分析】- 自动配置 Condition 注解 Condition 是 Spring 4.0 增加的条件判断功能,通过这个功能可以实现选择的创建 Bean 操作 👑 我们在使用 Spring 的时候,只需导入某个依赖的坐标,就可以直接通过 Autwired 注…...

简明易懂的JVM理解
文章目录简明易懂的JVM和GC理解写在前面Java虚拟机(JVM)的组成基本介绍结构类加载子系统(ClassLoader SubSystem)介绍类加载过程类加载过程小结双亲委派模型(Parent-Delegation Model)简介优点Java9的类加载的委派关系变动双亲委派模型小结运行时数据区(Runtime Data Areas)介绍…...

新考纲下的PMP考试有多难?
PMP考试在6月25号考试结束后,在网上引起一片哗然,新考纲领域与考点的转变使得考试难度加大:PMP考试敏捷和混合内容比重大,考试难度加大很多;考题更加注重考生的知识应用能力,领域更宽; 接下来我…...

朗润国际期货:知名投行/大佬打Call记
知名投行/大佬打Call记 2023年知名投行/大佬看好哪些投资标的 中国股市 高盛(2023年1月):将上涨15% 花旗(2023年1月):上半年会成为投资两点 摩根大通(2022年11月):M…...
遗传算法及Python实现
0 建议学时 4学时 1 人工智能概述 2020中国人工智能产业年会在苏州召开,会上发布的《中国人工智能发展报告2020》显示,过去十年(2011-2020) ,中国人工智能专利申请量达389571件,占全球总量的74.7%,位居世界第一。 报…...

零基础 Ubuntu 20.04.01 下搭建51单片机开发环境[开源编译器SDCC]
原创首发于CSDN,转载请注明出处,谢谢! 文章目录为何会在Linux下开发单片机个人系统环境与所用开发板安装开源编译器 sdccSTC MCU ISP 闪存工具 stcgal 的安装单片机代码的编译与测试|编写主代码 main.c|使用 sdcc 编译…...

手摸手快速入门 正则表达式 (Vue源码中的使用)
vue2源码 在 vue2 源码的 src\compiler\parser\html-parser.js 文件中 里面有大量的正则表达式,如下图 可以看到非常的长,不是我说,就前几行,如果没有相关的 正则表达式 的工具,我可能就被劝退了😭 这里…...

TCP/IP网络协议族分成及其每层作用
1、可以分为应用层、传输层、网络层、链路层 2、各层的作用 应用层(可以想象成是快递打包过程) 决定了向用户提供应用服务时通信的活动,将要进行的操作或者数据进行一个打包。 传输层(可以理解为选择顺丰、圆通等快递公司) 提供数据传输的方…...
)
041、子序列类型问题(labuladong)
子序列类型问题 一、经典动态规划:编辑距离 基于labuladong的算法网站,经典动态规划:编辑距离; 总结: 一般来说涉及到两个字符串的问题,需要依赖上一次的各种操作,一般使用dp tableÿ…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
