第十三届蓝桥杯省赛 C++ A 组 F 题、Java A 组 G题、C组 H 题、Python C 组 I 题——青蛙过河(AC)
目录
- 1.青蛙过河
- 1.题目描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.数据范围
- 7.原题链接
- 2.解题思路
- Ac_code
- 1.C++
- 2.Java
1.青蛙过河
1.题目描述
小青蛙住在一条河边, 它想到河对岸的学校去学习。小青蛙打算经过河里 的石头跳到对岸。
河里的石头排成了一条直线, 小青蛙每次跳跃必须落在一块石头或者岸上。 不过, 每块石头有一个高度, 每次小青蛙从一块石头起跳, 这块石头的高度就 会下降 1 , 当石头的高度下降到 0 时小青蛙不能再跳到这块石头上(某次跳跃 后使石头高度下降到 0 是允许的)。
小青蛙一共需要去学校上 xxx 天课, 所以它需要往返 2x2x2x 次。当小青蛙具有 一个跳跃能力 yyy 时, 它能跳不超过 yyy 的距离。
请问小青蛙的跳跃能力至少是多少才能用这些石头上完 xxx 次课。
2.输入格式
输入的第一行包含两个整数 n,xn,xn,x, 分别表示河的宽度和小青蛙需要去学校 的天数。请注意 2x2x2x 才是实际过河的次数。
第二行包含 n−1n−1n−1 个非负整数 H1,H2,⋯,Hn−1H_1,H_2,⋯,H_{n-1}H1,H2,⋯,Hn−1, 其中 Hi>0H_i>0Hi>0表 示在河中与 小青蛙的家相距 iii 的地方有一块高度为 HiH_iHi 的石头,
Hi=0H_i =0Hi=0 表示这个位置没有石头。
3.输出格式
输出一行, 包含一个整数, 表示小青蛙需要的最低跳跃能力。
4.样例输入
5 1
1 0 1 0
5.样例输出
4
6.数据范围
1≤n≤105,1≤x≤109,1≤Hi≤104。1≤n≤10^5 ,1≤x≤10^9,1≤H i ≤10^ 4 。1≤n≤105,1≤x≤109,1≤Hi≤104。
7.原题链接
青蛙过河
2.解题思路
假设青蛙可以按照某条路线SSS从家跳往对岸,路线SSS上所有的石子高度均减1,这个操作等价于“青蛙从对岸按照路线SSS反向跳回家,路线SSS上所有的石子高度均减1”。
这也说明,判断小青蛙能否往返2x2x2x次,等价于判断小青蛙能否从左往右跳重复2x2x2x次。
由题目可以发现,设小青蛙的跳跃能力为yyy,当小青蛙跳跃能力yyy越大,越容易满足“重复2x次”的约束,即求解的yyy存在单调性:
- 当yyy越大时,小青蛙每次可以跳的范围更大,可以跳更少的步数到达对岸,即更容易重复2x2x2x次,当y=ny=ny=n时,无需经过任何石子就可以跳到对岸。
- 当yyy越小时,小青蛙需要使用更多的步数才能到达对岸,更不容易满足“重复2x2x2x次”的约束。
本题最终需要求解的是:恰好满足约束的最小的yyy 答案存在单调性,显然可以用二分答案的算法进行求解,初始区间[l,r]=[1,n][l,r]=[1,n][l,r]=[1,n]:
- 求出区间[l,r][l,r][l,r]的中点midmidmid,mid=(l+r)//2mid=(l+r)//2mid=(l+r)//2
- 判断当小青蛙跳跃能力等于midmidmid时,能否从左往右跳重复2x2x2x次
- 如果可以,则更新ans=midans=midans=mid,调整搜索区间为[l,mid−1][l,mid-1][l,mid−1](求最小值,因此调整右端点)
- 否则,调整搜索区间为[mid+1,r][mid+1,r][mid+1,r]
- 如果l>rl > rl>r,终止循环,否则回到111
二分答案将求解最值问题转换成判定性问题,问题转变成当跳跃能力等于yyy时,判断小青蛙能否从左往右跳2x2x2x次。
小青蛙最开始位于0处,跳跃能力等于yyy,需要重复跳跃2x2x2x次,则首先要求从1−y1-y1−y的石子高度必须大于等于2x2x2x,不然小青蛙迈出的第一步都无法重复2x2x2x次。
这个结论可以推广——“所有长度为yyy的区间中石子高度之和必须大于等于2x2x2x”。
- 如果所有长度为yyy的区间中,石子高度之和等于2x:2x:2x:则存在Hi=Hi+yH_i=H_{i+y}Hi=Hi+y,则只要保证第一步在[1,y][1,y][1,y]中选择一个可以跳跃的石子iii,则后续跳跃只需从当前位置iii跳到i+yi+yi+y即可。这样可以保证重复2x2x2x次;
- 如果所有长度为yyy的区间中,石子高度之和大于2x2x2x:**则可以考虑去除某些石子的高度,从而构造出情况1,此时也是可以保证重复2x2x2x次的;
- 如果可以重复跳跃2x2x2x次,所有区间长度为yyy的区间中石子高度之和大于等于2x2x2x:对于任意区间[i,i+y][i,i+y][i,i+y],每次跳跃必须在区间中落脚。利用反证法,如果不在区间[i,i+y][i,i+y][i,i+y]中落脚,等价于从iii的左边跳到了i+yi+yi+y的右边,此时跳跃长度超过了能力上限yyy,因此不合法。也就是说,每次跳跃对于任意长度等于yyy的区间都落脚1次,重复2x2x2x次则说明该区间石子之和大于等于2x2x2x。
通过上面三点可以证明:“当跳跃能力等于yyy时重复2x2x2x次”等价于“所有区间长度等于yyy的区间石子高度之和大于等于2x2x2x”,利用这个结论进行二分答案的判定即可。
实现过程中事先预处理前缀和,从而可以O(1)O(1)O(1)求解区间和,时间复杂度O(nlogn)O(n\log n)O(nlogn)。
实际上使用双指针,维护区间和始终大于 2x2x2x,得到的最小区间长度则是答案,这样可做到 O(n)O(n)O(n) 的复杂度。
Ac_code
1.C++
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;LL n, x;
void solve()
{cin >> n >> x;std::vector<LL> s(n + 1);for (int i = 1; i < n; ++i) {cin >> s[i];s[i] += s[i - 1];}//最后一块石头,也就是终点,可以无限跳s[n] = 1e18;int l = 1, r = n;auto check = [&](int g) {for (int i = 0; i + g <= n; ++i) {int r = i + g;if (s[r] - s[i] < 2 * x) return false;}return true;};while (l < r) {int mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}cout << r << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
2.Java
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc=new Scanner(System.in);int n=sc.nextInt();long x=sc.nextLong();long []arr=new long[n+1];for (int i=1;i<n;i++){arr[i]=sc.nextLong()+arr[i-1];}arr[n]=100000000000L;int l=0;int ans=0;for (int r=1;r<=n;r++){if (arr[r]-arr[l]>= 2*x){ans=Math.max(ans,r-l);l+=1;}}System.out.println(ans);}
}
相关文章:
)
第十三届蓝桥杯省赛 C++ A 组 F 题、Java A 组 G题、C组 H 题、Python C 组 I 题——青蛙过河(AC)
目录1.青蛙过河1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路Ac_code1.C2.Java1.青蛙过河 1.题目描述 小青蛙住在一条河边, 它想到河对岸的学校去学习。小青蛙打算经过河里 的石头跳到对岸。 河里的石头排成了一条直线, 小青蛙每次跳跃…...

django项目实战四(django+bootstrap实现增删改查)进阶时间控件
接上一篇《django项目实战三(djangobootstrap实现增删改查)进阶分页》 知识点: 使用bootstrap-datepicker实现时间控件 一、优化layout.html模版 主要新增2个块 {% block css %}{% endblock %}{% block js %}{% endblock %} {% load static…...

Jetpack之ViewModel
The ViewModel class is a business logic or screen level state holder. 上面是官方给的定义,ViewModel 类是业务逻辑或屏幕级状态持有者。 一、业务逻辑持有者 在此之前,无论是MVC模式,还是MVP模式,在视图层,都会…...
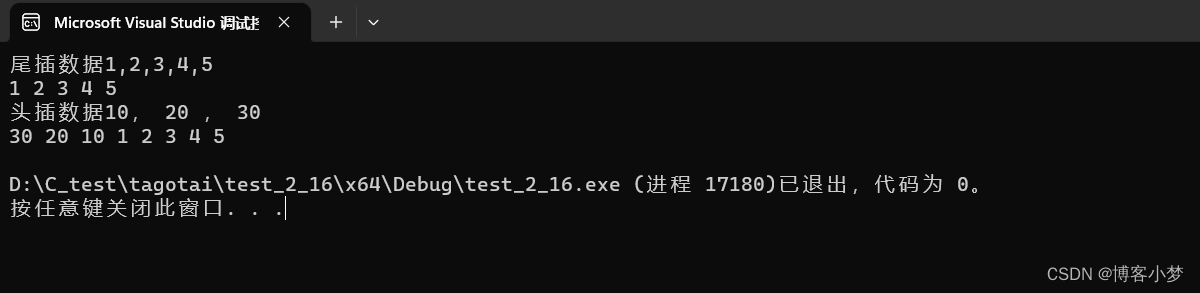
追梦之旅【数据结构篇】——详解C语言动态实现顺序表
详解C语言动态实现顺序表~😎前言🙌顺序表概念及结构🙌功能函数的具体实现分析:🙌尾插函数具体实现:尾删函数具体实现:头插函数具体实现:头删插函数具体实现:任意插函数具…...
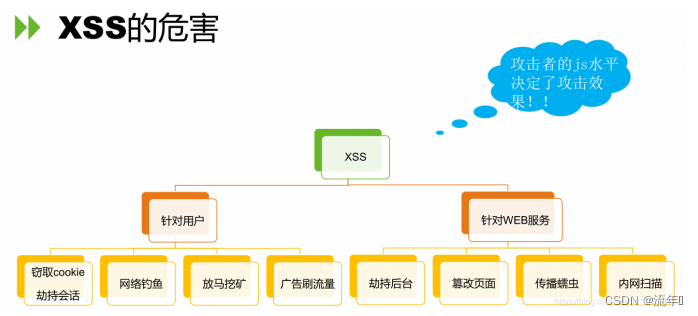
xss基础
目录标题一、XSS的原理二、XSS漏洞分类1、反射型xss2、存储型XSS3、基于DOM的XSS三、XSS漏洞的危害及验证四、XSS漏洞的黑盒测试五、XSS漏洞的白盒测试一、XSS的原理 跨站脚本攻击XSS(Cross Site Scripting),为了不和层叠样式表(…...
移动WEB开发二、流式布局
零、文章目录 文章地址 个人博客-CSDN地址:https://blog.csdn.net/liyou123456789个人博客-GiteePages:https://bluecusliyou.gitee.io/techlearn 代码仓库地址 Gitee:https://gitee.com/bluecusliyou/TechLearnGithub:https:…...

分享在线预约系统制作步骤_在线预约链接怎么做
在微信小程序上进行在线预约,不管是商家还是顾客,都可以自由选择时间,顾客还可以通过预约小程序,了解到所选服务的详情和功能特色,不必等到去店内听介绍,顾客能节省等候时间,商家能解放招待人力…...

【每日一题Day125】LC1326灌溉花园的最少水龙头数目 | 动态规划 贪心
灌溉花园的最少水龙头数目【LC1326】 在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。 花园里总共有 n 1 个水龙头,分别位于 [0, 1, ..., n] 。 给你一个整数 n 和一个长度为 n 1 的整数数组 ranges ,其中 …...
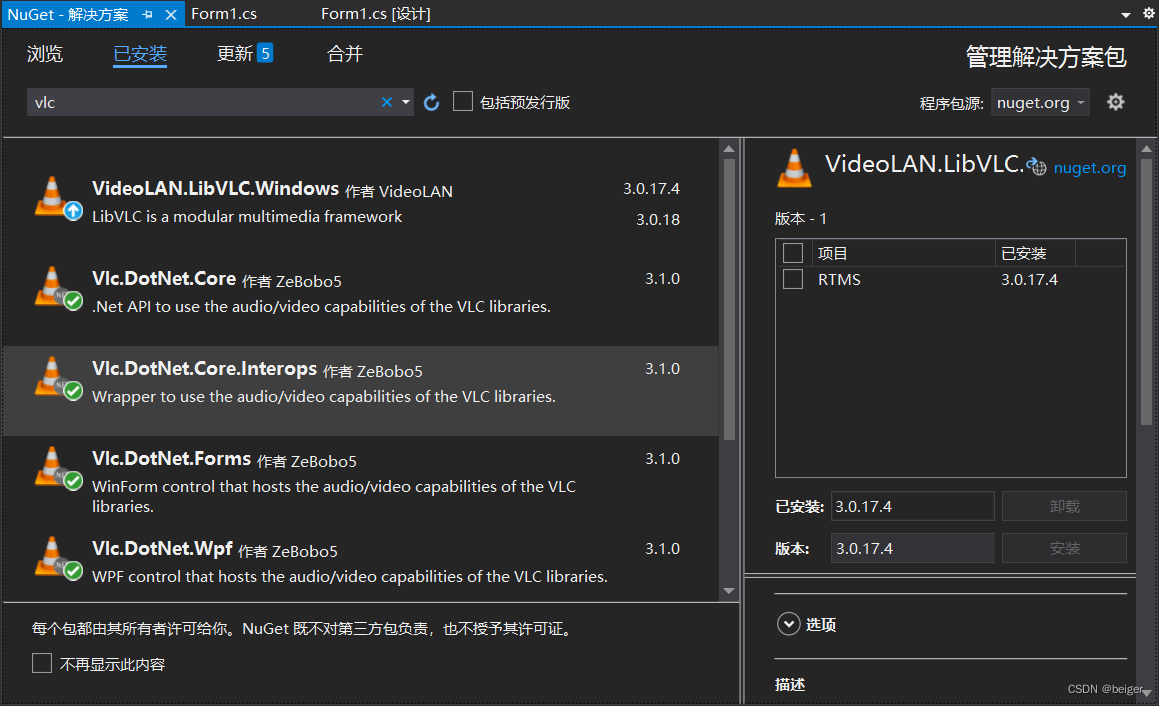
C# FFmpeg推流Vlc.DotNet拉流优化参数
FFmpeg是流媒体开源神器,视频转换、剪裁包括推流,无所不能,很多系统都是基于其开发的。拉流可以用FFplay,但是不利于集成到自己的代码中,因此拉流选择了Vlc.DotNet。 在使用中,仅使用默认参数,…...
)
pnpm v8版本升级变化关注点(前瞻速攻版)
前言 pnpm v8.0.0-alpha.0 版本已经发布,包含少量变化,但其中还是有令人在意的点的。 本文将默认读者拥有大部分 pnpm v7 版本的知识储备,进行 v8 版本的前瞻速攻。 安装方法 目前通过指定 Tag 方式可以安装 v8 alpha 版: npm…...
Python基础-环境安装
Python安装1.下载PythonPython网址:https://www.python.org/进入Python官网,点击Downloads,选择自己对应的操作系统(此处以Windows为例)在左侧的稳定发行版中,选择一个3.5版本以上的,然后点击对…...

重载、重写、重构概念辨析
首先,重载、重写、重构都表现为方法名相同 重载 重载(overload),表示同一类的方法之间的关系,至少有以下其中一种情况 参数个数不同参数类型不同参数顺序不同 注意,返回值类型不同不能作为重载依据 重…...
第九章 - 多表查询(join,left join 等)与合并查询(union union all)
第九章 - 多表查询(join,left join 等)与合并查询(union)交叉链接(笛卡尔积)内连接查询外连接查询左链接: left join右链接:right join组合查询 union & union all使…...
matplotlib学习笔记(持续更新中…)
目录 1. 安装,导入 2. figure,axes(图形,坐标图形) 2.1 figure对象 2.2 axes对象 2.3 代码演示 2.3 subplot() 方法 3. 图表的导出 3.1 savefig() 方法 3.2 代码演示 1. 安装,导入 pip install m…...
STM32 SystemInit()函数学习总结
拿到程序后如何看系统时钟?User文件夹——system_stm32f4xx程序,先找systemcoreclock(系统时钟)但是这里这么多个系统时钟应该如何选择?点击魔法棒,然后点击C/C可以看到define的是F40_41XXX.USE这一款 ,对应着就找出了…...
【Spring Boot 原理分析】- 自动配置
【Spring Boot 原理分析】- 自动配置 Condition 注解 Condition 是 Spring 4.0 增加的条件判断功能,通过这个功能可以实现选择的创建 Bean 操作 👑 我们在使用 Spring 的时候,只需导入某个依赖的坐标,就可以直接通过 Autwired 注…...

简明易懂的JVM理解
文章目录简明易懂的JVM和GC理解写在前面Java虚拟机(JVM)的组成基本介绍结构类加载子系统(ClassLoader SubSystem)介绍类加载过程类加载过程小结双亲委派模型(Parent-Delegation Model)简介优点Java9的类加载的委派关系变动双亲委派模型小结运行时数据区(Runtime Data Areas)介绍…...

新考纲下的PMP考试有多难?
PMP考试在6月25号考试结束后,在网上引起一片哗然,新考纲领域与考点的转变使得考试难度加大:PMP考试敏捷和混合内容比重大,考试难度加大很多;考题更加注重考生的知识应用能力,领域更宽; 接下来我…...

朗润国际期货:知名投行/大佬打Call记
知名投行/大佬打Call记 2023年知名投行/大佬看好哪些投资标的 中国股市 高盛(2023年1月):将上涨15% 花旗(2023年1月):上半年会成为投资两点 摩根大通(2022年11月):M…...
遗传算法及Python实现
0 建议学时 4学时 1 人工智能概述 2020中国人工智能产业年会在苏州召开,会上发布的《中国人工智能发展报告2020》显示,过去十年(2011-2020) ,中国人工智能专利申请量达389571件,占全球总量的74.7%,位居世界第一。 报…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
