排序之插入排序
文章目录
- 前言
- 一、直接插入排序
- 1、基本思想
- 2、直接插入排序的代码实现
- 3、直接插入排序总结
- 二、希尔排序
- 1、希尔排序基本思想
- 2、希尔排序的代码实现
- 3、希尔排序时间复杂度
前言
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
一、直接插入排序
1、基本思想
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
例如当有如下一组有序的数组。当分别将10、5、0按照插入排序的思想插入到数组中时,
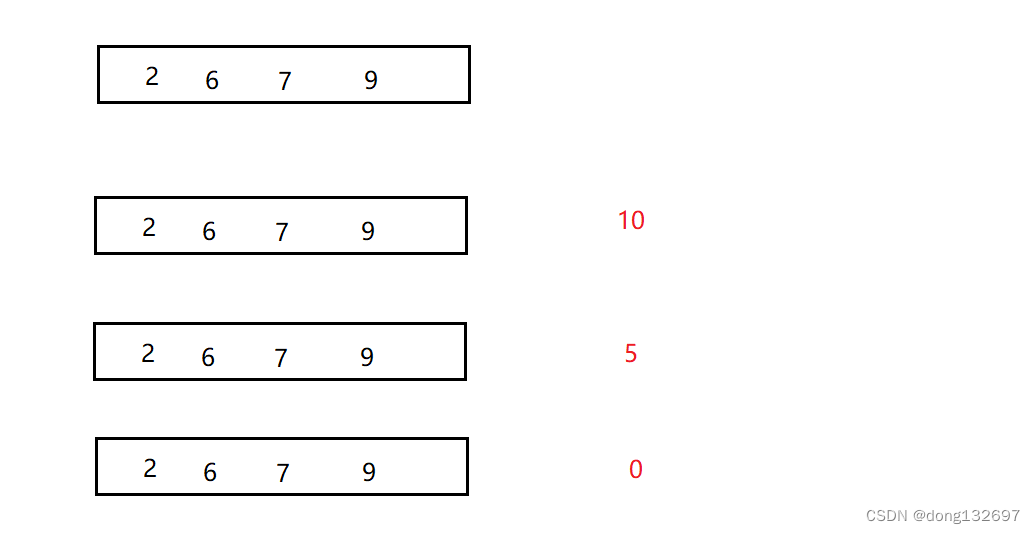
此时插入的数据要与数组最后一位进行比较,如果比最后一位大,就插入到数组最后一位的后面;
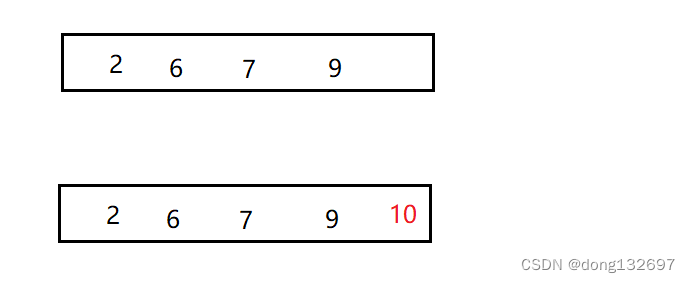
如果比数组中最后一位小,就将数组中最后一位元素向后移一位,然后插入的数据与倒数第二个数据进行比较,就这样依次循环下去 。
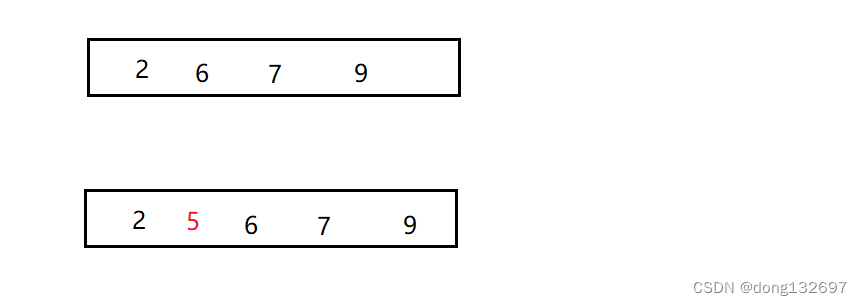
如果插入的数据比数组中所有数据都小,此时插入的数据会被插入到数组下标为0的位置,即作为数组的第一个元素。
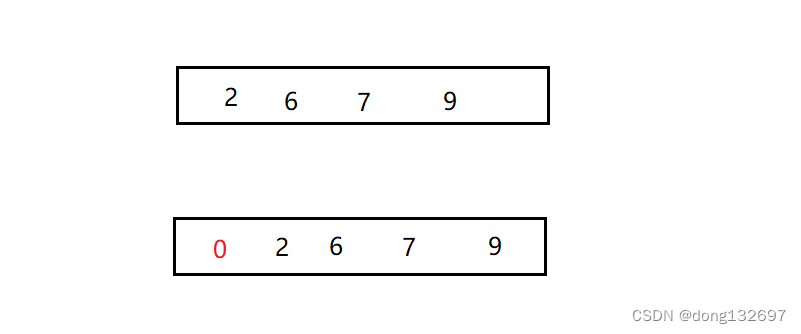
上述的操作就是插入排序的单趟排序,即在有序区间,插入一个数使这个区间继续有序。
2、直接插入排序的代码实现
直接写出来插入排序来将数组排序比较困难,我们可以先写出来单趟排序,即当有一个数组的[0,end]有序,把end+1位置的值插入数组中,然后保持数组的[0,end+1]有序。
例如有如下数组。
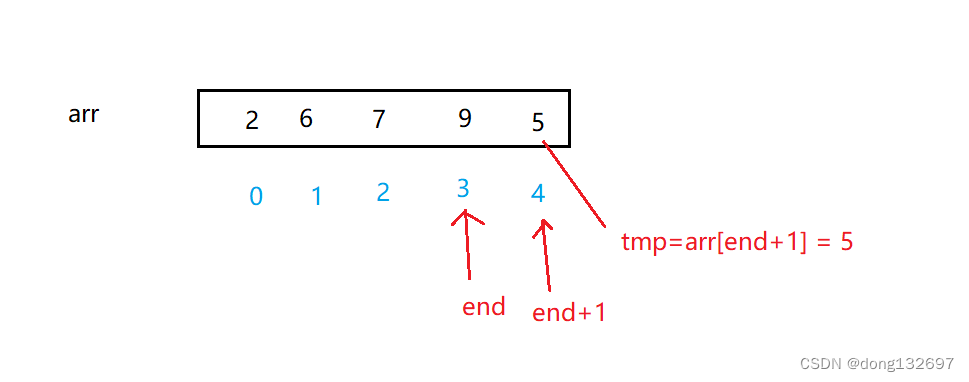
此时数组中end+1的值为5,该值小于数组中end位置的值,此时就用tmp记录end+1位置的值,然后将end的值向后移一位,移到end+1位置。然后将end–,此时再将end位置的值与tmp比较。
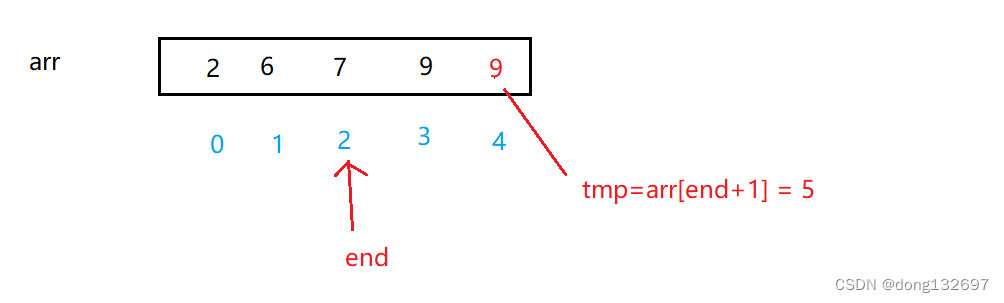
此时end位置的值比tmp小,则说明tmp的值就应该插入到end位置之后,此时直接将end+1位置赋值为tmp即可。然后数组中[0,end+1]有序。
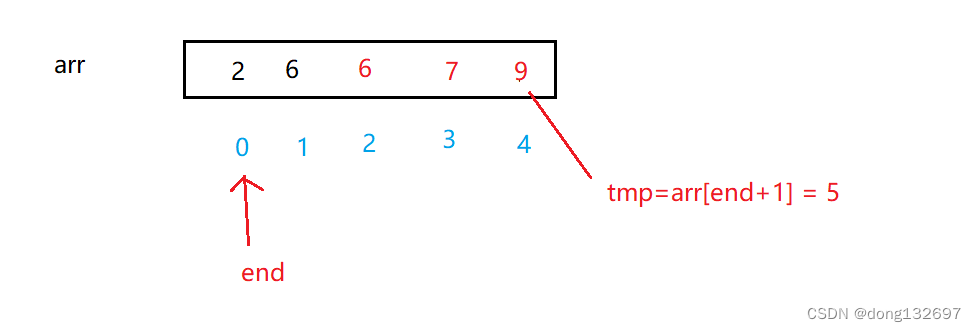
上述就是单趟排序。
void InsertSort(int* arr, int n)
{//[0,end]有序,把end+1位置的值插入,保持有序int end;//将tmp赋值为数组中下标为end+1位置的值int tmp = arr[end + 1];//如果end没有到数组头部,就继续比较while (end >= 0){//如果tmp小于arr[end],就将此时end的数据向后移,然后将end--,使tmp与新的end位置的值比较if (tmp < arr[end]){arr[end + 1] = arr[end];end--;}else{//如果满足条件就跳出循环break;}}//此时end为数组中第一个小于tmp的位置,此时将end+1位置赋值为tmp。//如果当end为-1时,即插入的数据tmp比数组头元素还小,此时end+1刚好为0,即让插入的数据tmp作为新的数组头部。arr[end + 1] = tmp;
}
通过上述的操作我们明白了插入排序排序数组时的单趟操作,当我们有一个长度为n的数组arr时,我们先将end置为0,然后依次将数组首元素之后的元素依次进行插入,当end为n-2时,此时end+1为n-1,即为数组最后一个元素的插入。我们就可以再写一个循环将上面的代码套入其中,并且控制end的值从0到n-2。
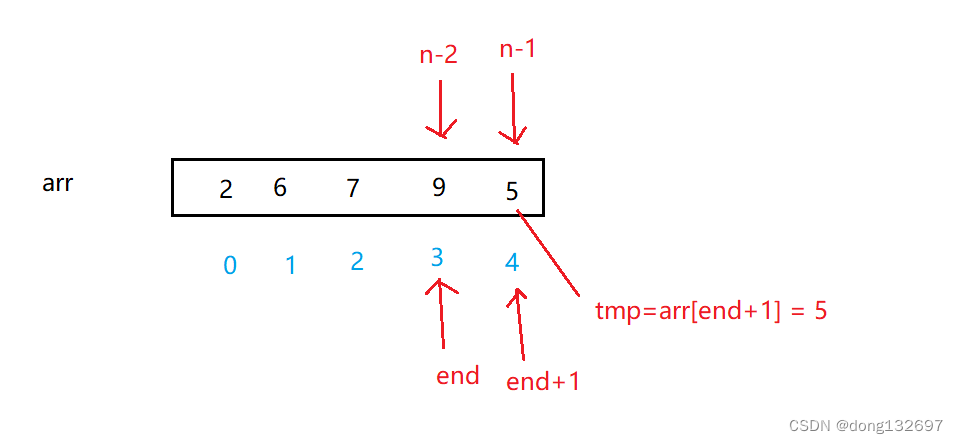
void InsertSort(int* arr, int n)
{int i = 0;//控制end的值,将数组中的元素从首元素后面开始依次进行插入。for (i = 0; i < n-1; i++){//[0,end]有序,把end+1位置的值插入,保持有序int end=i;//将tmp赋值为数组中下标为end+1位置的值int tmp = arr[end + 1];while (end >= 0){//如果tmp小于arr[end],就将此时end的数据向后移,然后将end--,使tmp与新的end位置的值比较if (tmp < arr[end]){arr[end + 1] = arr[end];end--;}else{break;}}//此时end为数组中第一个小于tmp的位置,此时将end+1位置赋值为tmp。//如果当end为-1时,即插入的数据tmp比数组头元素还小,此时end+1刚好为0,即让插入的数据tmp作为新的数组头部。arr[end + 1] = tmp;}}
3、直接插入排序总结
直接插入排序的特性总结:
1.元素集合越接近有序,直接插入排序算法的时间效率越高
2.时间复杂度:O(N^2)
3.空间复杂度:O(1),它是一种稳定的排序算法
4.稳定性:稳定
直接插入排序的最坏时间复杂度为O(N^2),即当数组为逆序时。
最优时间复杂度为O(N),即当数组为顺序有序/接近顺序有序。
二、希尔排序
由上面总结的直接插入排序的最优时间复杂度可知,当数组的顺序接近有序时,直接插入排序的性能可以得到提高,并且能达到O(N)的级别,而希尔排序就是利用了这一点。
1、希尔排序基本思想
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成gap个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后gap=gap/gap,取gap,重复上述分组和排序的工作。当到达gap=1时,所有记录在统一组内排好序。
希尔排序分为两步。
1、预排序(接近顺序有序)
2、直接插入排序(有序)
例如有如下的一组逆序的数据。
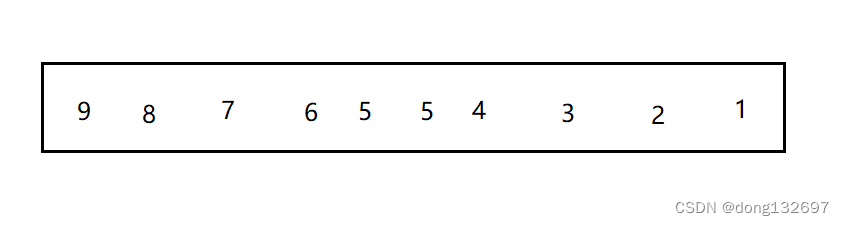
假设gap为3,即将该组数据分为如图所示的三组数据,
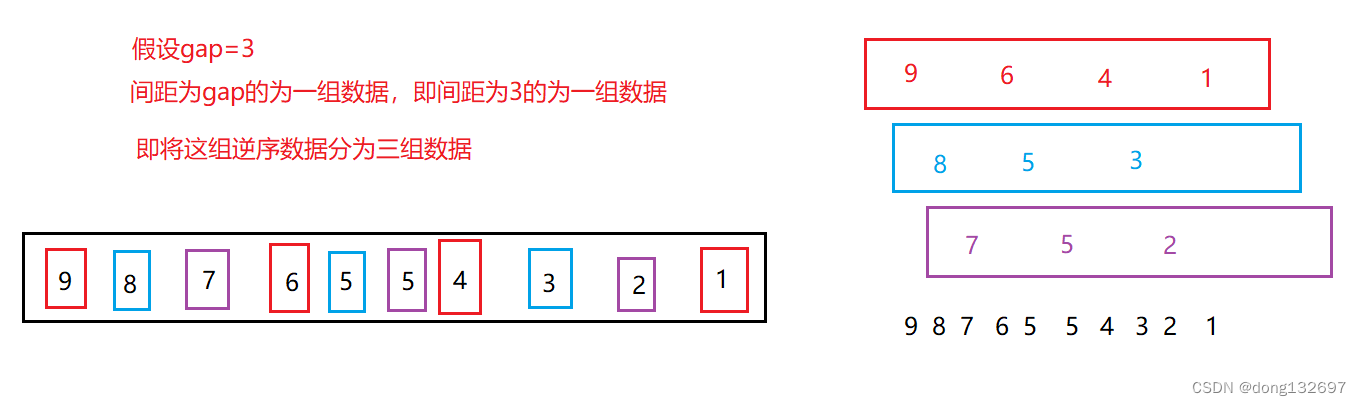
然后将这三组数据分别进行直接插入排序,此时该组数据的排序虽然没有达到顺序有序,但是相比于原来的逆序,此时该组数据已经接近顺序有序。
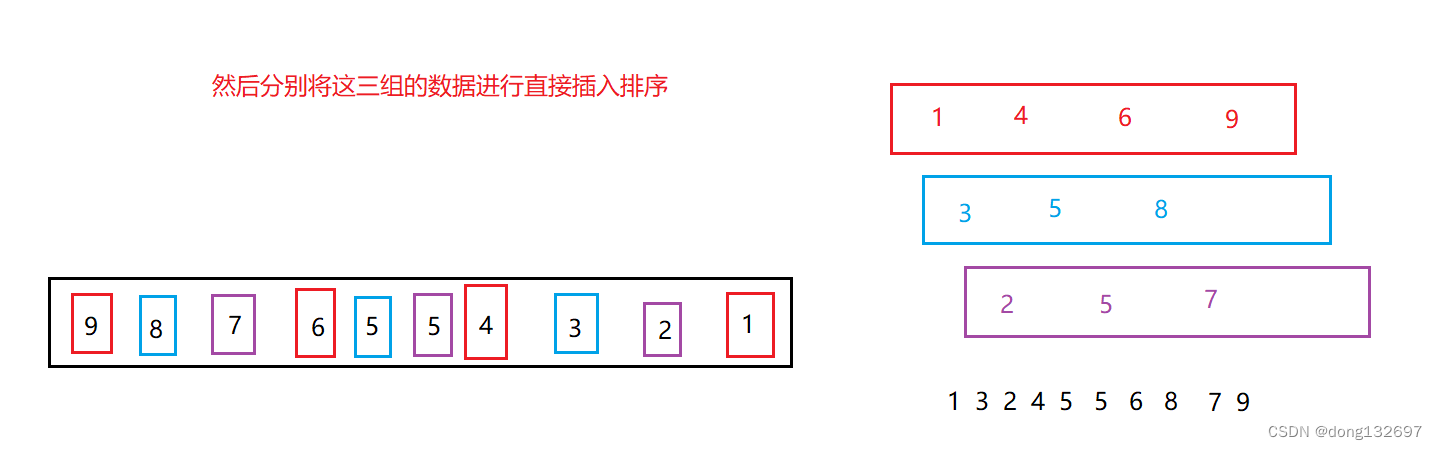
此时将该组数据总体进行直接插入排序,这样相比于原来逆序时就直接进行直接插入排序,效率提高了很多。并且我们可以看出当gap=1时,此时就是进行直接插入排序。
2、希尔排序的代码实现
我们可以像实现直接插入排序一样,先了解希尔排序的一组数据中的单趟排序。
即将分成的3组数据的红色组数据先进行直接插入排序。
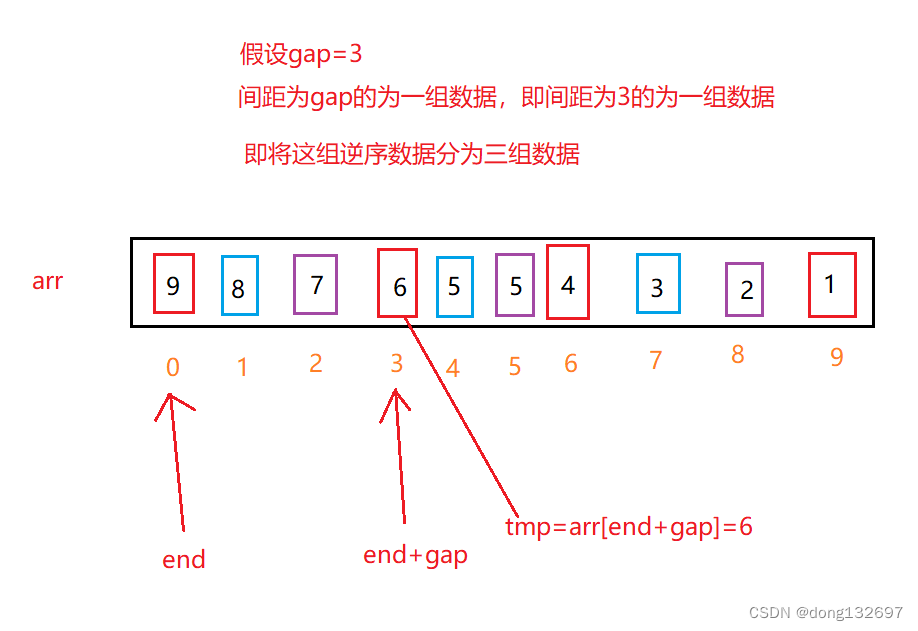
此时将end+gap位置的值赋值为end位置的值。
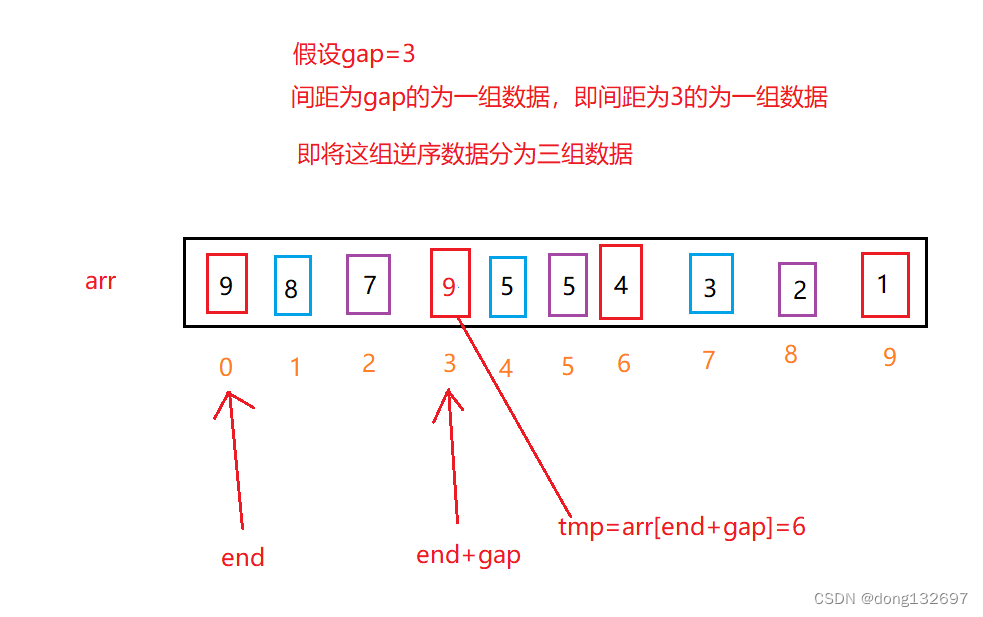
然后end = end - gap,此时end已经为负数,但是end+gap为0,刚好为数组的首位,所以将arr[end+gap]的位置存入tmp,即将tmp插入到数组的首位。
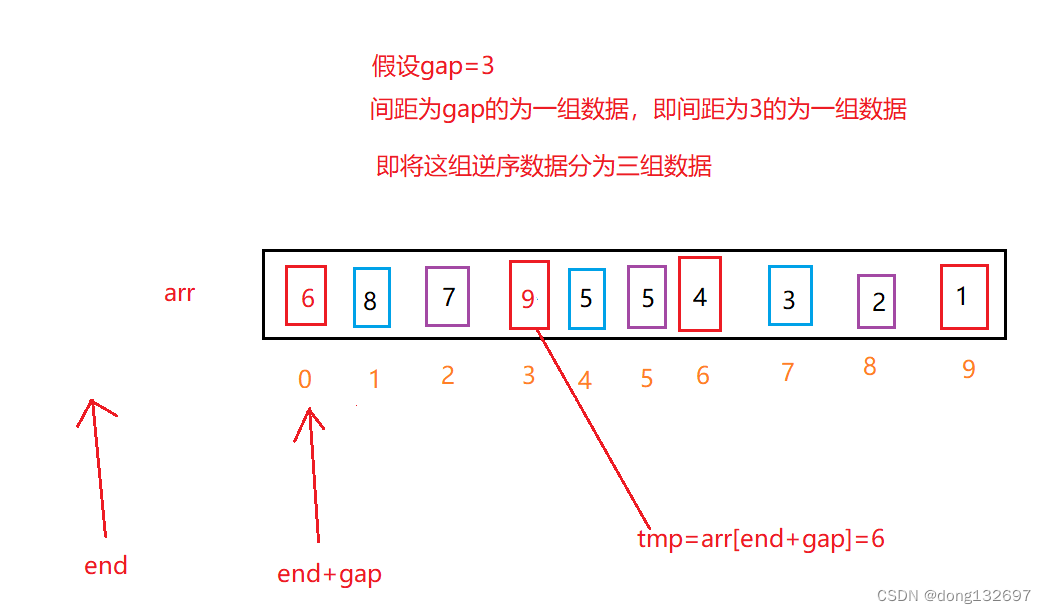
下列代码就实现了上述的操作。
void ShellSort(int* arr, int n)
{int gap = 3;int end = 0;//将tmp赋值为数组中end位置后gap位置的值int tmp = arr[end + gap];while (end >= 0){//如果tmp的值小于此时end位置的值if (tmp < arr[end]){//就将end+gap位置的值赋值为end位置的值,arr[end + gap] = arr[end];//然后将end向后移gap个距离,继续和tmp比较end -= gap;}else{break;}}//此时end位置的值是小于tmp的,将end+gap位置的值赋值为tmparr[end + gap] = tmp;
}
但是上述代码只是将红色数组中的一个数据完成了直接插入排序,下面我们要将红色数组的数据都进行直接插入排序,则需要加一个循环,然后使end的值每次都向后改变。
void ShellSort(int* arr, int n)
{int gap = 3;int i = 0;for (i = 0; i < n - gap; i += gap){int end = i;//将tmp赋值为数组中end位置后gap位置的值int tmp = arr[end + gap];while (end >= 0){//如果tmp的值小于此时end位置的值if (tmp < arr[end]){//就将end+gap位置的值赋值为end位置的值,arr[end + gap] = arr[end];//然后将end向后移gap个距离,继续和tmp比较end -= gap;}else{break;}}//此时end位置的值是小于tmp的,将end+gap位置的值赋值为tmparr[end + gap] = tmp;}}
上述代码只是将红色数组完成了直接插入排序,但是蓝色数组和紫色数组还没有完成直接插入排序,所以需要再次套入一个循环,将蓝色数组和紫色数组也完成直接插入排序操作。此时才算将gap组数都分别在各自组内进行了直接插入排序,此时数组arr中的数据接近顺序有序。
void ShellSort(int* arr, int n)
{int gap = 3;int i = 0;for (i = 0; i < gap; i++){int j = 0;for (j = i; j < n - gap; j += gap){int end = j;//将tmp赋值为数组中end位置后gap位置的值int tmp = arr[end + gap];while (end >= 0){//如果tmp的值小于此时end位置的值if (tmp < arr[end]){//就将end+gap位置的值赋值为end位置的值,arr[end + gap] = arr[end];//然后将end向后移gap个距离,继续和tmp比较end -= gap;}else{break;}}//此时end位置的值是小于tmp的,将end+gap位置的值赋值为tmparr[end + gap] = tmp;}}
}
上述代码嵌套了三层循环,会让人觉得循环太多,其实可以将外面的循环去掉,然后将第二层循环的i += gap变为i++。达到的效果和上面的代码一致,上面代码是将gap组数依次进行直接插入排序,而这个代码是将第一组数的一个进行直接插入排序后,然后将第二组数进行直接插入排序,然后将第三组数进行直接插入排序。这样两个代码达到的效果是一样的。
void ShellSort(int* arr, int n)
{int gap = 3;int j = 0;for (j = 0; j < n - gap; j ++){int end = j;//将tmp赋值为数组中end位置后gap位置的值int tmp = arr[end + gap];while (end >= 0){//如果tmp的值小于此时end位置的值if (tmp < arr[end]){//就将end+gap位置的值赋值为end位置的值,arr[end + gap] = arr[end];//然后将end向后移gap个距离,继续和tmp比较end -= gap;}else{break;}}//此时end位置的值是小于tmp的,将end+gap位置的值赋值为tmparr[end + gap] = tmp;}
}
到这里只完成了希尔排序的第一个步骤,即预排序,而想要将数组中的数据都有顺序,还需要将数组进行直接插入排序。预排序的目的是让数组中的数据达到基本顺序有序,这样使用直接插入排序对数组排序时效率就会提高。
希尔排序的gap该怎么选择呢?
由上面我们可以直到当排升序时,gap越大,大的数更快到后面,小的数可以更快到前面,但是越不接近有序。
排升序时,gap越小,越接近有序,当gap==1时,就是直接插入排序。
当数组中数据为10000个时,此时如果选择gap=3,则预排序和进行直接排序插入的复杂度差不多。当数组中数据为100个时,此时将gap=30,则经过预排序后数组中的数据还是没有达到基本顺序有序。
此时我们可以将gap设置为一个变化的值。
void ShellSort(int* arr, int n)
{int gap = n;int j = 0;//gap>1时都为预排序,并且随着gap越来越小,数组越来越接近有序while (gap > 1){//随着gap越来越小,数组中的数据越接近有序,当gap==1时,就是直接插入排序gap = gap / 3 + 1; // gap / 3 + 1保证了最后一次gap=1,即最后一次为直接插入排序for (j = 0; j < n - gap; j++){int end = j;//将tmp赋值为数组中end位置后gap位置的值int tmp = arr[end + gap];while (end >= 0){//如果tmp的值小于此时end位置的值if (tmp < arr[end]){//就将end+gap位置的值赋值为end位置的值,arr[end + gap] = arr[end];//然后将end向后移gap个距离,继续和tmp比较end -= gap;}else{break;}}//此时end位置的值是小于tmp的,将end+gap位置的值赋值为tmparr[end + gap] = tmp;}}}
3、希尔排序时间复杂度
希尔排序的时间复杂度很难求,我们只需记住它的时间复杂度接近于O(N^1.3)。
《数据结构(C语言版)》— 严蔚敏

相关文章:

排序之插入排序
文章目录 前言一、直接插入排序1、基本思想2、直接插入排序的代码实现3、直接插入排序总结 二、希尔排序1、希尔排序基本思想2、希尔排序的代码实现3、希尔排序时间复杂度 前言 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大…...
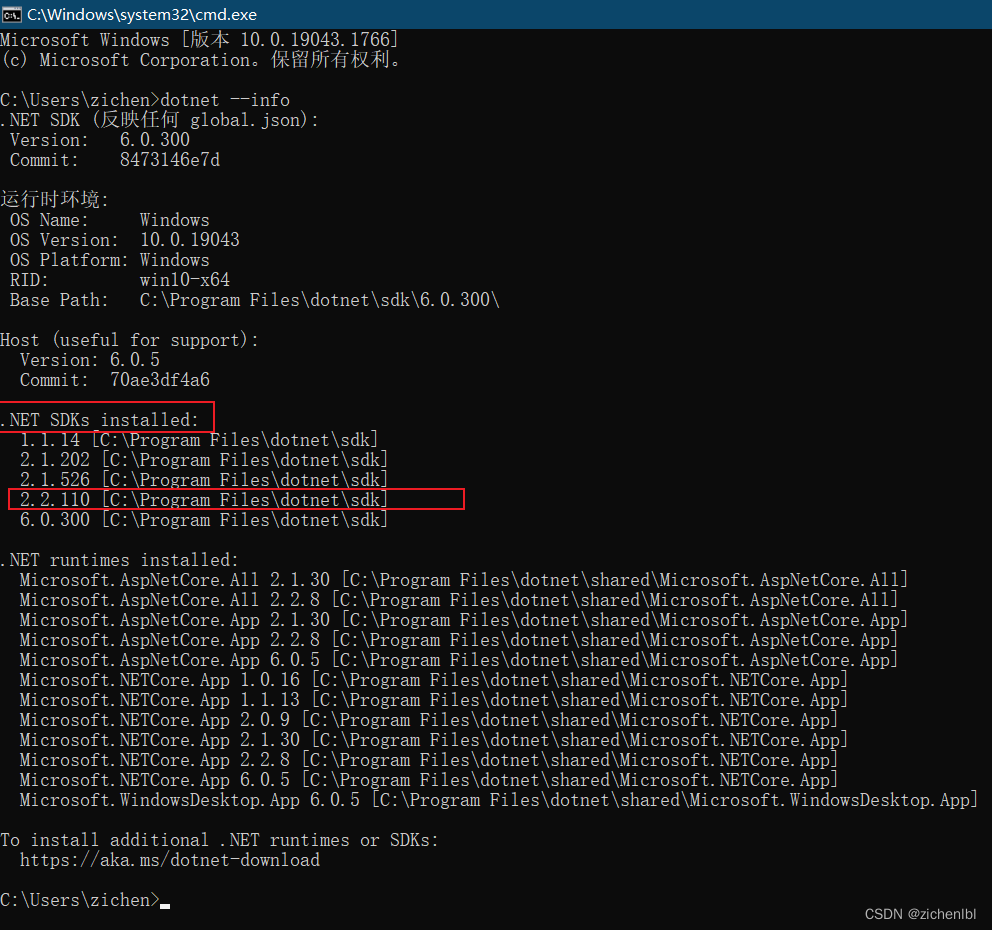
c# - - - 安装.net core sdk
如图,安装的是.Net Core 2.2版本 查看安装成功...
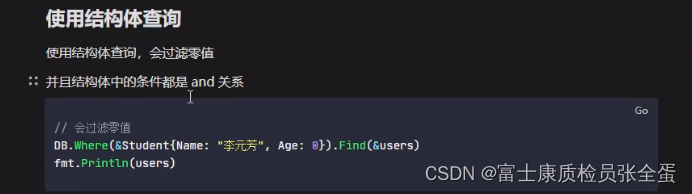
Golang Gorm 高级查询之where + find
插入测试数据 package mainimport ("fmt""gorm.io/driver/mysql""gorm.io/gorm" )type Student struct {ID int64Name string gorm:"size:6"Age intEmail *string }func (*Student) TableName() string {return "student&q…...

【LeetCode】30 天 Pandas 挑战
一、笔记 1.对某列进行筛选 df[(df[column1]条件1) | (df[column2]条件2) & (df[column3]条件3)][[columns]]真题: (一)条件筛选——1.大的国家(一)条件筛选——2.可回收且低脂的产品(一)…...

头歌MYSQL——课后作业2 数据表中数据的插入、修改和删除
第1关:数据表中插入一条记录,对指定字段赋值 任务描述 本关任务:在library数据库的reader数据表中插入一条数据 姓名xm为林团团,电话号码dhhm为13507311234,其余字段取默认值 显示数据表的所有数据 为了完成本关任务,…...

Maven的profiles多环境配置
一个项目通常都会有多个不同的运行环境,例如开发环境,测试环境、生产环境等。而不同环境的构建过程很可能是不同的,例如数据源配置、插件、以及依赖的版本等。每次将项目部署到不同的环境时,都需要修改相应的配置,这样…...

go 协程
golang中的并发是函数相互独立运行的能力。Goroutines是并发运行的函数。Golang提供了 如何实现go协程 只需要在函数前面加上go即可 go task()package mainimport ("fmt""time" )func show(msg string) {for i : 0; i < 5; i {fmt.Printf("msg: …...
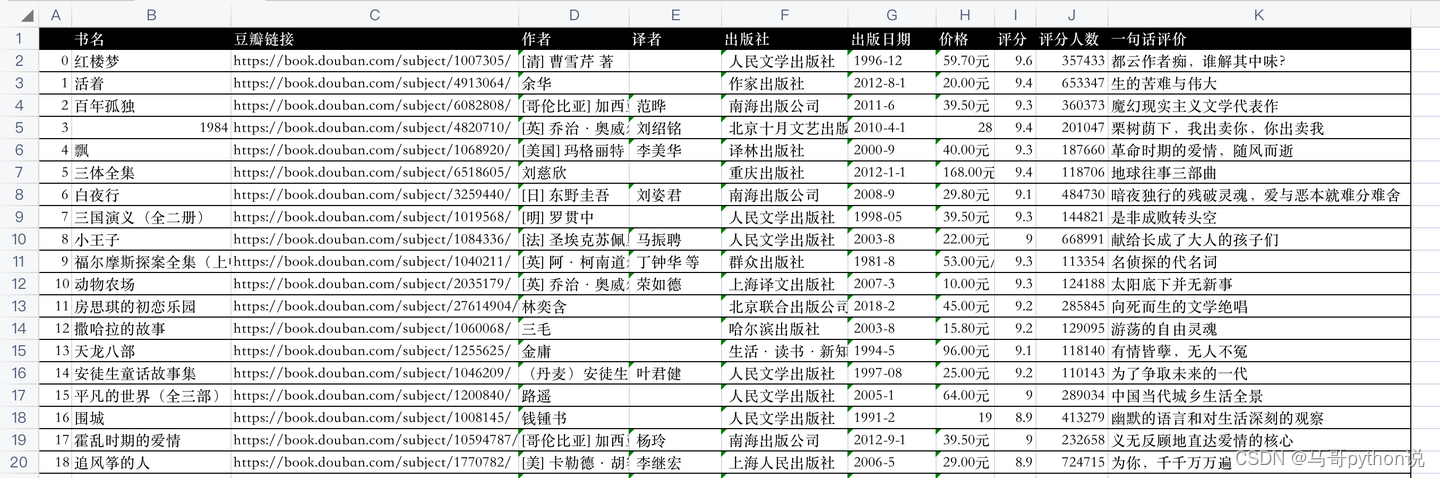
【python爬虫案例】用python爬豆瓣读书TOP250排行榜!
文章目录 一、爬虫对象-豆瓣读书TOP250二、python爬虫代码讲解三、讲解视频四、完整源码 一、爬虫对象-豆瓣读书TOP250 您好,我是 马哥python说 ,一名10年程序猿。 今天我们分享一期python爬虫案例讲解。爬取对象是,豆瓣读书TOP250排行榜数…...

Qt中 gui 模块和 widgets 模块的区别
1. gui 模块提供了基本的图形系统抽象层,包括QPaintDevice、QPainter等类,这些类构成了Qt的绘图基础。 2. widgets 模块在 gui 模块的基础上,提供了完整的桌面级用户界面控件,如按钮、列表、滑块等。这些控件继承自更基础的图形类。 3. gui 模块是更底层的图形功能,widgets模…...
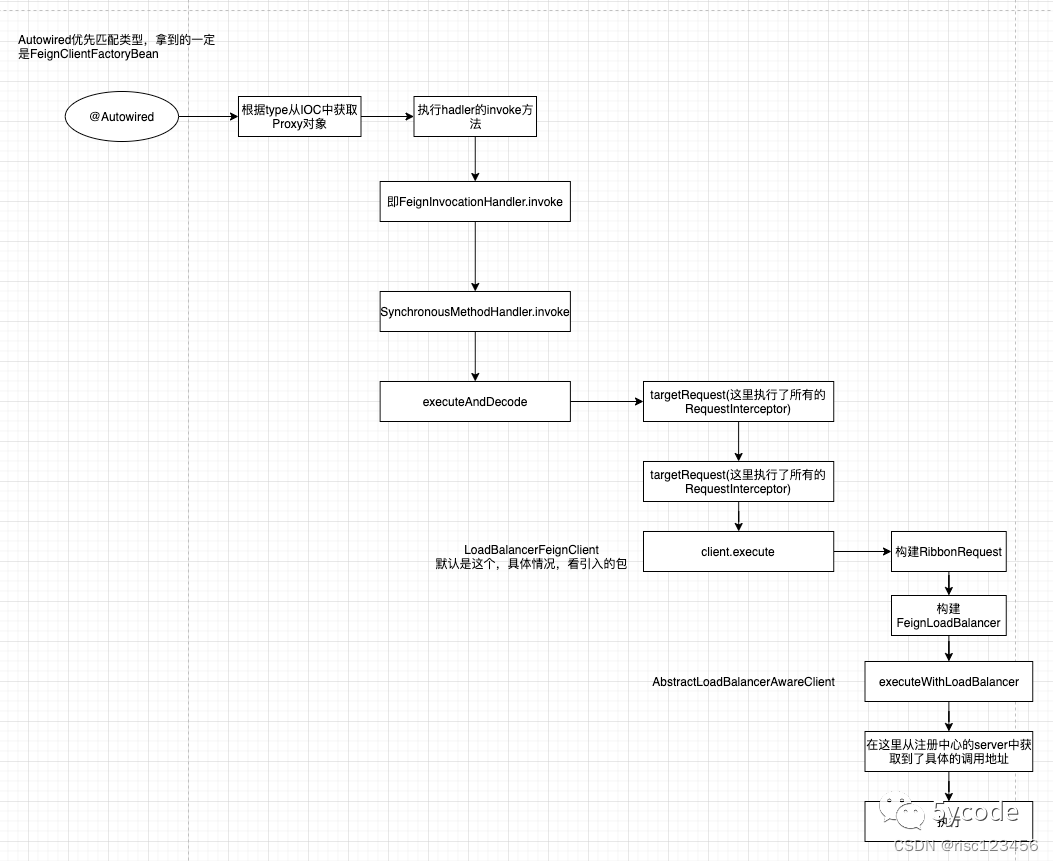
feign调用流程
...
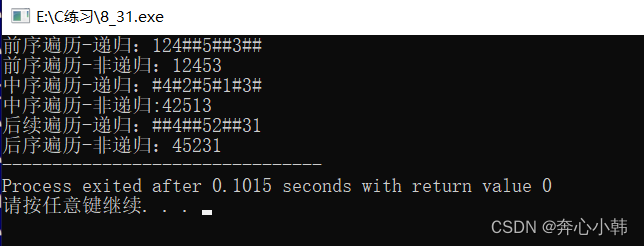
15-数据结构-二叉树的遍历,递归和非递归
简介: 本文主要是代码实现,二叉树遍历,递归和非递归(用栈)。主要为了好理解,直接在代码处,加了详细注释,方便复习和后期默写。主要了解其基本思想,为后期熟练应用…...
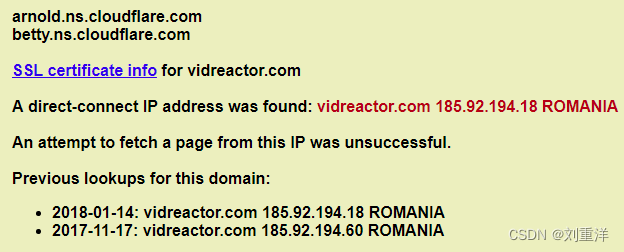
最新绕过目标域名CDN进行信息收集技术
绕过目标域名CDN进行信息收集 1.CDN简介及工作流程 CDN(Content Delivery Network,内容分发网络)的目的是通过在现有的网络架构中增加一层新的Cache(缓存)层,将网站的内容发布到最接近用户的网…...

overlayfs
参考:How containers work: overlayfs how overlays work Overlay filesystems, also known as “union filesystems” or “union mounts” let you mount a filesystem using 2 directories: a “lower” directory, and an “upper” directory. Basically: t…...

Mysql中九种索引失效场景分析
表数据: 索引情况: 其中a是主键,对应主键索引,bcd三个字段组成联合索引,e字段为一个索引 情况一:不符合最左匹配原则 去掉b1的条件后就不符合最左匹配原则了,导致索引失效 情况二ÿ…...

Android RecyclerView 之 列表宫格布局的切换
前言 RecyclerView 的使用我就不再多说,接下来的几篇文章主要说一下 RecyclerView 的实用小功能,包括 列表宫格的切换,吸顶效果,多布局效果等,今天这篇文章就来实现一下列表宫格的切换,效果如下 一、数据来…...

妈妈的爱依然深沉
村里的孩子为了买化肥,跟城里官老爷们借了好多钱。 那几年庄稼转手很快,不是用来吃的,因此借钱成本很高,大概LPR加100bp。 后来村里孩子终于发现庄稼终究只能用来吃,不再热衷买卖化肥。可是官老爷们的金融生意还要继续…...
)
net.ResolveTCPAddr(“tcp6“, address)
尝试解析 "www.google.com" 的IPv6地址。如果解析成功,程序将打印出解析后的IP地址、端口以及区域信息。如果解析失败,程序将打印出错误信息。 需要注意的是,如果 "www.google.com" 没有IPv6地址,或者本地网络…...
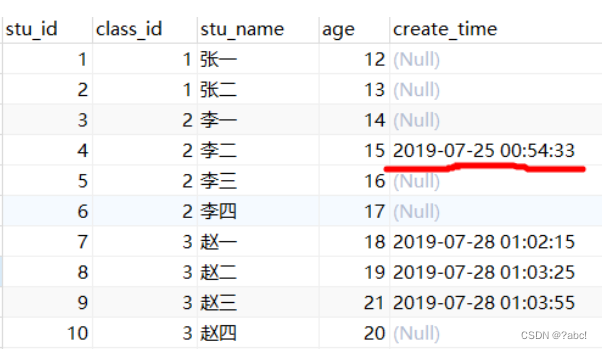
mysql和mybatisPlus实现:datetime类型的字段范围查询
前提说明 数据库在存储数据时,我们为了精确一下时间,便会把改时间类型的字段设置为datetime类型; 在过滤数据库数据时,我们又需要对该字段进行一个范围的过滤 由此,便出现了这篇博客 datetime数据类型 在MySQL中,datetime数据类型用于保存日期和时间的值。它的格式为Y…...

学习笔记:用ROS接收rosbag发布的topic
用ROS接收 bag.open发布的topic python语言 要使用ROS接收保存在rosbag文件中的话题消息,可以按照以下步骤进行操作: 1.首先,请确保你已经安装了ROS和相关的依赖。 2.创建一个ROS功能包(或使用现有的功能包)来处理…...
LAMP架构介绍配置命令讲解
LAMP架构介绍配置命令讲解 一、LAMP架构介绍1.1概述1.2LAMP各组件的主要作用1.3各组件的安装顺序 二、编译安装Apache httpd服务---命令讲解1、关闭防火墙,将安装Apache所需的软件包传到/opt/目录下2、安装环境依赖包3、配置软件模块4、编译安装5、优化配置文件路径…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
