15-数据结构-二叉树的遍历,递归和非递归
简介:
本文主要是代码实现,二叉树遍历,递归和非递归(用栈)。主要为了好理解,直接在代码处,加了详细注释,方便复习和后期默写。主要了解其基本思想,为后期熟练应用打基础。
遍历的意义,就是为了实现在二叉树上,进行各种操作,给每个结点都光顾到位,到根节点时,进行当前节点的操作。
目录:
目录
一、前序遍历。
1.1前序遍历—递归
1.2前序遍历—非递归
二、中序遍历
2.1中序遍历—递归
2.2中序遍历—非递归
三、后序遍历
3.1后序遍历—递归
3.2后序遍历—非递归
五、总代码
5.1代码
5.2运行结果图
一、前序遍历。
1.1前序遍历—递归
简介:前序为:先访问根结点,再访问其左孩子,再访问右孩子(根左右)。
//前序遍历,递归
void PreOrder(BTNode *node)
{if(node==NULL)//当前结点为空时,返回上一层递归空间 {printf("#");return;}//结点非空时 visit(node);PreOrder(node->lchild);PreOrder(node->rchild);
}1.2前序遍历—非递归
简介:非递归,就是利用栈(就是一个存放树结点指针的数组,再加一个栈顶标记top),存放树节点的指针。树不为空的时候先入栈,随后,栈不为空时,再进行出栈操作。前序遍历出栈时,先出栈后,先访问该节点信息,随后再判断该节点是否有右孩子,有则,右孩子的指针存进栈中。再判断是否有左孩子,有则左孩子指针存进栈,
//前序遍历,非递归
void Stack_PreOrder(BTNode *node)
{if(node==NULL)//树为空,不处理return;//创建一个栈,存放树结点类型的地址 BTNode* Stack[10];int top=-1;//工作指针,随着p指针,记录树的当前结点位置 BTNode *p=NULL;//当树非空时,进行操作 if(node !=NULL){//入栈 top++;Stack[top]=node;//随后进行出栈操作,只有栈非空时,才可出栈 while(top != -1){//取出此时栈顶元素 p=Stack[top];top--;//然后进行访问当前结点的相关操作 visit(p);//访问完根,在看该根的右孩子,入栈 ,因为是栈,先进后出,而前序为根左右,根出来后,右入栈,之后左入栈,最后出栈是栈顶出 if(p->rchild!=NULL){top++;Stack[top]=p->rchild;}//访问完右孩子,在看该根的左孩子,入栈 if(p->lchild!=NULL){top++;Stack[top]=p->lchild;} } }
}二、中序遍历
2.1中序遍历—递归
简介:左根右。不理解为啥的,可以画图,每进入一个新的函数,便是一个新的空间。
//中序遍历-递归
void InOrder(BTNode *node)
{if(node==NULL){printf("#");return;}InOrder(node->lchild);visit(node);InOrder(node->rchild);
}2.2中序遍历—非递归
简介:其实,栈也好,递归也罢,需要操作的,仅为两步,第一步为进入新树的一些列操作。操作完,进入第二步,进到另一方向孩子树中,该树中的操作,还是先进性第一步,再进行第二部,
思想:中序遍历非递归操作,最外圈来个do-while循环,先执行,再判断。如果栈内非空,或者该结点不为空,都进行中序遍历操作。
do-while里面的操作:先左子树操作:一直遍历,入栈元素,随后给指针地址换成该节点的左孩子,就是一直遍历到左孩子为空,才停止。至此,左根右中的左操作完毕。随后出栈元素,进行左根右中的根操作,访问根节点。至此,为第一步的操作。随后第二部,进入方向的树中,即结点指针换为右孩子地址,
//中序遍历-非递归
void StackInOrder(BTNode *node)
{if(node==NULL)//树为空,则不处理return;printf("中序遍历-非递归:");BTNode* p=node;BTNode* Stack[10];int top=-1;do{//当结点不为空时,入栈,并进入左孩子。 ——访问左孩子 while(p!=NULL){top++;Stack[top]=p;p=p->lchild;}//一直遍历左,遍历到空,此时,出栈p=Stack[top];top--;visit(p);//访问根 p=p->rchild;//根访问完,随后,访问右孩子。随后,右孩子中,又是新的树,然后再进行左根右操作,形成循环,从上面再来一圈。 }while(top!=-1 || p!=NULL);//只要树不为空,或者栈内有元素,就一直进行操作。 } 三、后序遍历
3.1后序遍历—递归
简介:左右根。
// 后序遍历-递归
void PostOrder(BTNode *node)
{if(node==NULL){printf("#");return;}PostOrder(node->lchild);PostOrder(node->rchild);visit(node);
}3.2后序遍历—非递归
简介:这个比较麻烦,不过还是利用描边法去做,根据描边法,根节点被访问两次,第一次时入栈时,第二次时判断是否出栈时,就看从那一层返回到根节点的,如果从右孩子返回的,则进行出栈操作,先记录当前结点,再出栈。否则,则进行右子树结点的出栈,
这里面,跟中序,略有不同,入栈和出栈的情况需要判断,所以需要用栈顶指针时刻对比。
先跟根结点入栈,随后当栈内不为空时,一直进行遍历操作。先进性第一步的入栈操作(当上层遍历,即不是栈顶指针的左孩子又不是右孩子时,更新工作指针为左孩子,随后进行一直左孩子入栈操作)第二步,左孩子到底了,此时需要面临出栈,因此给当前栈顶元素取出来,如果该树没有左孩子,或者pre与右孩子地址相同,则进行出栈操作,并记录出栈前的指针p,否则则给右孩子入栈。
void StackPostOrder(BTNode *node)
{printf("后序遍历-非递归:");if(node==NULL)return; BTNode *p=node;//工作指针 BTNode *pre=NULL;//表示上层结点位置 //栈 BTNode *Stack[10];int top=-1;//先跟根节点入栈,为了方便第一次判断top++;Stack[top]=p;do{//先判断上层结点是否遍历过,没有,则进行左子树都入栈,入到底if(pre!=Stack[top]->lchild && pre!=Stack[top]->rchild){p=Stack[top]->lchild;//上次没有遍历过左右孩子,那么开始栈顶元素的左孩子入栈操作。while(p!=NULL){top++;Stack[top]=p;p=p->lchild; } }//左孩子方向弄到底后,开始判断,是否需要出栈输出。p=Stack[top];//记录此时的栈顶元素if(p->rchild==NULL || pre==p->rchild)//如果右孩子为空,或者上一层和当前结点的右孩子相等,则输出 {pre=p;//记录当前结点地址 visit(p);//输出 top--;//输出了,栈内指针减少 }else{top++;Stack[top]=p->rchild;//右孩子入栈 } }while(top!=-1);
}五、总代码
5.1代码
#include <stdio.h>
#include <stdlib.h>
//创建树,孩子链表
typedef struct BTNode
{int data;struct BTNode *rchild,*lchild;}BTNode;
//创建树结点,并初始化
BTNode* BuyNode(int x)
{BTNode* node=(BTNode*)malloc(sizeof(BTNode));node->data=x;node->lchild=NULL;node->rchild=NULL;return node;
}
//手动创建树
BTNode* CreatTree()
{BTNode* node1=BuyNode(1);BTNode* node2=BuyNode(2);BTNode* node3=BuyNode(3);BTNode* node4=BuyNode(4);BTNode* node5=BuyNode(5);node1->lchild=node2;node1->rchild=node3;node2->lchild=node4;node2->rchild=node5;return node1;
}
//访问当前结点时的操作
void visit(BTNode *node)
{printf("%d",node->data);
}
//前序遍历,递归
void PreOrder(BTNode *node)
{if(node==NULL)//当前结点为空时,返回上一层递归空间 {printf("#");return;}//结点非空时 visit(node);PreOrder(node->lchild);PreOrder(node->rchild);
}
//前序遍历,非递归
void Stack_PreOrder(BTNode *node)
{if(node==NULL)return;printf("前序遍历-非递归:");//创建一个栈,存放树结点类型的地址 BTNode* Stack[10];int top=-1;//工作指针,随着p指针,记录树的当前结点位置 BTNode *p=NULL;//当树非空时,进行操作 if(node !=NULL){//入栈 top++;Stack[top]=node;//随后进行出栈操作,只有栈非空时,才可出栈 while(top != -1){//取出此时栈顶元素 p=Stack[top];top--;//然后进行访问当前结点的相关操作 visit(p);//访问完根,在看该根的右孩子,入栈 ,因为是栈,先进后出,而前序为根左右,根出来后,右入栈,之后左入栈,最后出栈是栈顶出 if(p->rchild!=NULL){top++;Stack[top]=p->rchild;}//访问完右孩子,在看该根的左孩子,入栈 if(p->lchild!=NULL){top++;Stack[top]=p->lchild;} } }
}
//中序遍历-递归
void InOrder(BTNode *node)
{if(node==NULL){printf("#");return;}InOrder(node->lchild);visit(node);InOrder(node->rchild);
}
//中序遍历-非递归
void StackInOrder(BTNode *node)
{if(node==NULL)return;printf("中序遍历-非递归:");BTNode* p=node;BTNode* Stack[10];int top=-1;do{//当结点不为空时,入栈,并进入左孩子。 ——访问左孩子 while(p!=NULL){top++;Stack[top]=p;p=p->lchild;}//一直遍历左,遍历到空,此时,出栈p=Stack[top];top--;visit(p);//访问根 p=p->rchild;//根访问完,随后,访问右孩子。随后,右孩子中,又是新的树,然后再进行左根右操作,形成循环,从上面再来一圈。 }while(top!=-1 || p!=NULL);//只要树不为空,或者栈内有元素,就一直进行操作。 }
// 后序遍历-递归
void PostOrder(BTNode *node)
{if(node==NULL){printf("#");return;}PostOrder(node->lchild);PostOrder(node->rchild);visit(node);
}
//后序遍历-非递归
void StackPostOrder(BTNode *node)
{printf("后序遍历-非递归:");if(node==NULL)return; BTNode *p=node;//工作指针 BTNode *pre=NULL;//表示上层结点位置 //栈 BTNode *Stack[10];int top=-1;//先跟根节点入栈,为了方便第一次判断top++;Stack[top]=p;do{//先判断上层结点是否遍历过,没有,则进行左子树都入栈,入到底if(pre!=Stack[top]->lchild && pre!=Stack[top]->rchild){p=Stack[top]->lchild;//上次没有遍历过左右孩子,那么开始栈顶元素的左孩子入栈操作。while(p!=NULL){top++;Stack[top]=p;p=p->lchild; } }//左孩子方向弄到底后,开始判断,是否需要出栈输出。p=Stack[top];//记录此时的栈顶元素if(p->rchild==NULL || pre==p->rchild)//如果右孩子为空,或者上一层和当前结点的右孩子相等,则输出 {pre=p;//记录当前结点地址 visit(p);//输出 top--;//输出了,栈内指针减少 }else{top++;Stack[top]=p->rchild;//右孩子入栈 } }while(top!=-1);
}
int main()
{BTNode* root=CreatTree();//前序遍历打印printf("前序遍历-递归:"); PreOrder(root);//递归 printf("\n"); Stack_PreOrder(root);//非递归,栈来做 printf("\n"); printf("中序遍历-递归:");InOrder(root); printf("\n"); StackInOrder(root); printf("\n"); printf("后续遍历-递归:");PostOrder(root);printf("\n"); StackPostOrder(root);return 0;} 5.2运行结果图
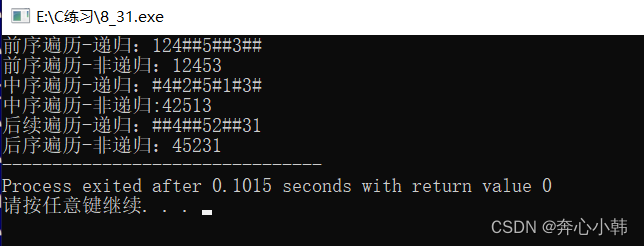
相关文章:

15-数据结构-二叉树的遍历,递归和非递归
简介: 本文主要是代码实现,二叉树遍历,递归和非递归(用栈)。主要为了好理解,直接在代码处,加了详细注释,方便复习和后期默写。主要了解其基本思想,为后期熟练应用…...
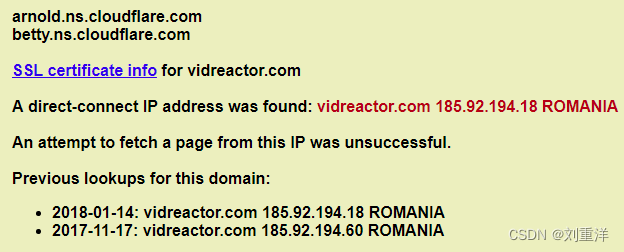
最新绕过目标域名CDN进行信息收集技术
绕过目标域名CDN进行信息收集 1.CDN简介及工作流程 CDN(Content Delivery Network,内容分发网络)的目的是通过在现有的网络架构中增加一层新的Cache(缓存)层,将网站的内容发布到最接近用户的网…...

overlayfs
参考:How containers work: overlayfs how overlays work Overlay filesystems, also known as “union filesystems” or “union mounts” let you mount a filesystem using 2 directories: a “lower” directory, and an “upper” directory. Basically: t…...

Mysql中九种索引失效场景分析
表数据: 索引情况: 其中a是主键,对应主键索引,bcd三个字段组成联合索引,e字段为一个索引 情况一:不符合最左匹配原则 去掉b1的条件后就不符合最左匹配原则了,导致索引失效 情况二ÿ…...

Android RecyclerView 之 列表宫格布局的切换
前言 RecyclerView 的使用我就不再多说,接下来的几篇文章主要说一下 RecyclerView 的实用小功能,包括 列表宫格的切换,吸顶效果,多布局效果等,今天这篇文章就来实现一下列表宫格的切换,效果如下 一、数据来…...

妈妈的爱依然深沉
村里的孩子为了买化肥,跟城里官老爷们借了好多钱。 那几年庄稼转手很快,不是用来吃的,因此借钱成本很高,大概LPR加100bp。 后来村里孩子终于发现庄稼终究只能用来吃,不再热衷买卖化肥。可是官老爷们的金融生意还要继续…...
)
net.ResolveTCPAddr(“tcp6“, address)
尝试解析 "www.google.com" 的IPv6地址。如果解析成功,程序将打印出解析后的IP地址、端口以及区域信息。如果解析失败,程序将打印出错误信息。 需要注意的是,如果 "www.google.com" 没有IPv6地址,或者本地网络…...
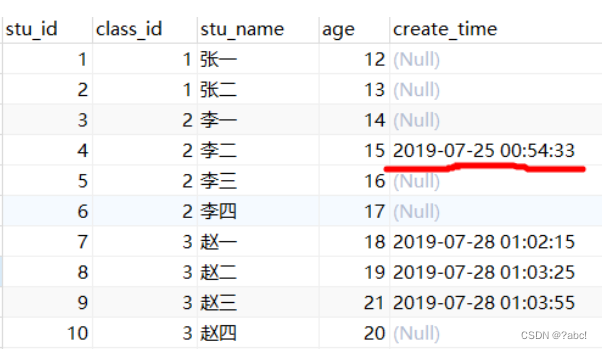
mysql和mybatisPlus实现:datetime类型的字段范围查询
前提说明 数据库在存储数据时,我们为了精确一下时间,便会把改时间类型的字段设置为datetime类型; 在过滤数据库数据时,我们又需要对该字段进行一个范围的过滤 由此,便出现了这篇博客 datetime数据类型 在MySQL中,datetime数据类型用于保存日期和时间的值。它的格式为Y…...

学习笔记:用ROS接收rosbag发布的topic
用ROS接收 bag.open发布的topic python语言 要使用ROS接收保存在rosbag文件中的话题消息,可以按照以下步骤进行操作: 1.首先,请确保你已经安装了ROS和相关的依赖。 2.创建一个ROS功能包(或使用现有的功能包)来处理…...
LAMP架构介绍配置命令讲解
LAMP架构介绍配置命令讲解 一、LAMP架构介绍1.1概述1.2LAMP各组件的主要作用1.3各组件的安装顺序 二、编译安装Apache httpd服务---命令讲解1、关闭防火墙,将安装Apache所需的软件包传到/opt/目录下2、安装环境依赖包3、配置软件模块4、编译安装5、优化配置文件路径…...
C语言之函数题
目录 1.乘法口诀表 2.交换两个整数 3.函数判断闰年 4.函数判断素数 5.计算斐波那契数 6.递归实现n的k次方 7.计算一个数的每位之和(递归) 8.字符串逆序(递归实现) 9.strlen的模拟(递归实现) 10.求…...
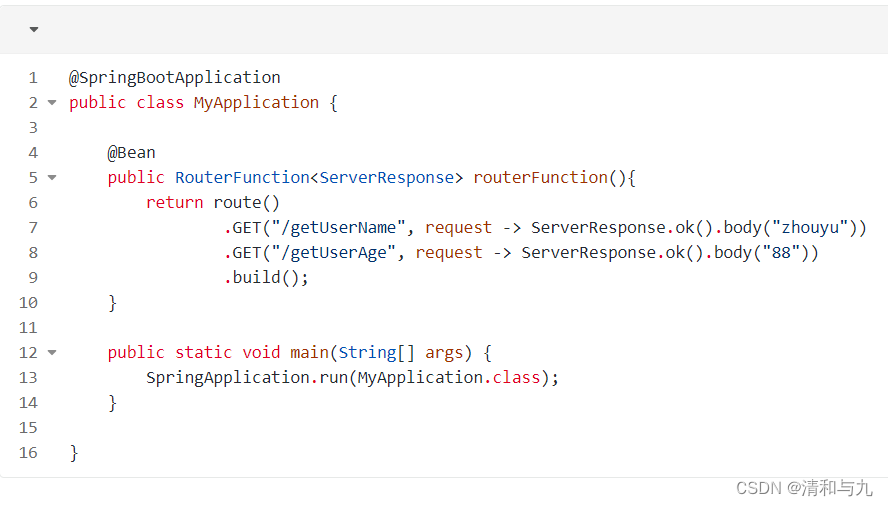
SpringBoot的四种handler类型
Controller ReuestMapping 实现Controller接口 使用Component将该类封装成一个Bean 实现HttpRequestHandler 实现RouterFunction...
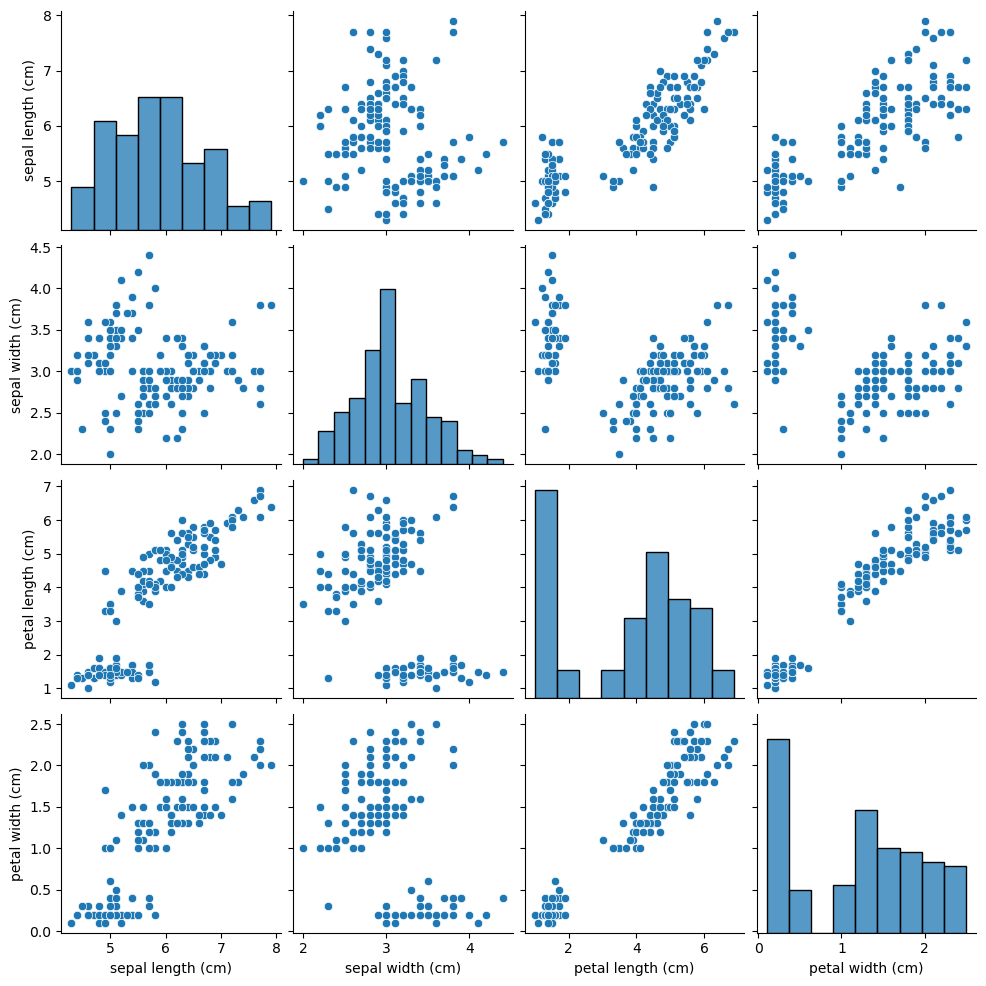
基于KNN算法的鸢尾花种类预测
导入数据 iris_data load_iris() iris_data.data[0:5, :]array([[5.1, 3.5, 1.4, 0.2],[4.9, 3. , 1.4, 0.2],[4.7, 3.2, 1.3, 0.2],[4.6, 3.1, 1.5, 0.2],[5. , 3.6, 1.4, 0.2]])# 特征值名称 iris_data.feature_names[sepal length (cm),sepal width (cm),petal length (cm…...

英语-面试
自我介绍 hi,my name is tzh,26 years old.I major in software engineering. I participate in the design and development of the social project and e-commerce project. I master java and algorithm. Im familiar with gateway,spring,springboot,springcloud,redis…...
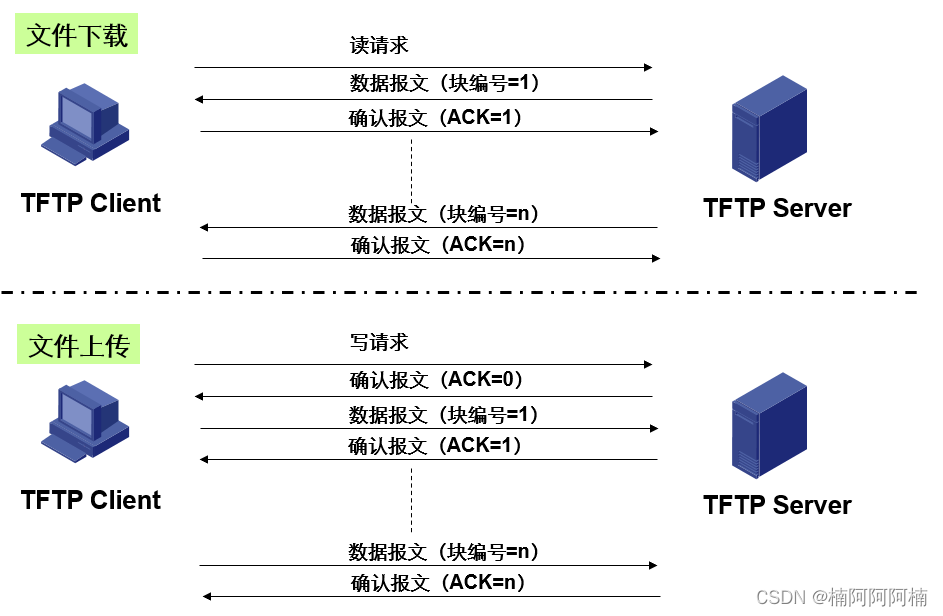
文件传输协议
文章目录 一、FTP1. 定义2. 端口3. 数据传输方式主动方式被动方式 二、TFTP三、常用命令 首先可以看下思维导图,以便更好的理解接下来的内容。 一、FTP 1. 定义 文件传输协议(FTP)是一种用于在客户端和服务器之间进行文件传输的标准网络协…...

Llama-2大模型本地部署研究与应用测试
最近在研究自然语言处理过程中,正好接触到大模型,特别是在年初chatgpt引来的一大波AIGC热潮以来,一直都想着如何利用大模型帮助企业的各项业务工作,比如智能检索、方案设计、智能推荐、智能客服、代码设计等等,总得感觉…...

白嫖idea
白嫖idea 地址 https://www.jetbrains.com/toolbox-app/...
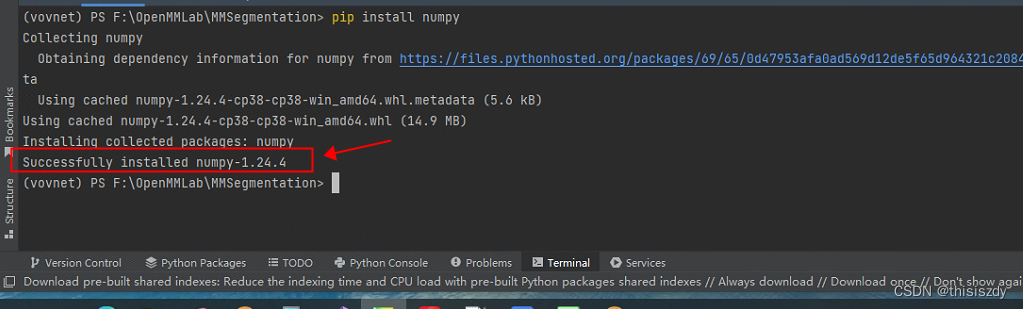
PyCharm切换虚拟环境
PyCharm切换虚拟环境 为了满足不同任务需要不同版本的包,可以在Anaconda或者Miniconda创建多个虚拟环境文件夹,并在PyCharm下切换虚拟环境。 解决方案 1、打开Ananconda Prompt 2、创建自己的虚拟环境 格式:conda create -n 虚拟环境名字…...
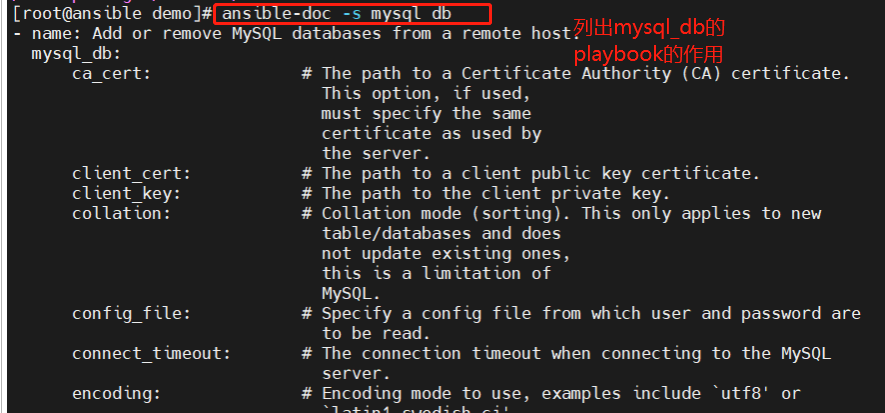
自动化运维工具-----Ansible入门详解
目录 一.Ansible简介 什么是Ansible? Ansible的特点 Ansible的架构 二.Ansible任务执行解析 ansible任务执行模式 ansible执行流程 ansible命令执行过程 三.Ansible配置解析 ansible的安装方式 ansible的程序结构(yum安装为例) ansibl…...
一、Mycat2介绍与下载安装
第一章 入门概述 1.1 是什么 Mycat 是数据库中间件。 1、数据库中间件 中间件:是一类连接软件组件和应用的计算机软件,以便于软件各部件之间的沟 通。 例子:Tomcat,web中间件。 数据库中间件:连接java应用程序和数据库…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
