【C语言】探讨蕴藏在表达式求解中的因素
🚩纸上得来终觉浅, 绝知此事要躬行。
🌟主页:June-Frost
🚀专栏:C语言
🔥该篇将探讨 操作符 和 类型转换 对表达式求解的影响。
目录:
- 隐式类型转换
- 算术转换
- 操作符的属性
- ❤️ 结语
隐式类型转换
C的整型算术运算总是至少以缺省(默认)整型类型的精度来进行的。为了获得这个精度,表达式中的字符和短整型操作数在使用之前被转换为普通整型,这种转换称为整型提升。
整型提升规则:
整形提升是按照变量的数据类型的符号位来提升的。
如果是无符号的整形提升,那么高位补0。
为了更好的理解这样的概念,将举一个例子来解释:
#include<stdio.h>
int main()
{char a = 5;char b = 127;char c = a + b;printf("%d\n", c);return 0;
}
-
char a = 5;
5是整型类型,32个bit,补码是00000000 00000000 00000000 00000101,将5存储到a中,a是有符号char类型,只有8个bit,所以要发生截断,将低位的 00000101 存储到a中。 -
char b = 127
同理,127的补码是 00000000 00000000 00000000 01111111 ,存储b时发生截断,所以将低位的 01111111 存储到b中。 -
char c = a + b;
这里的操作数 a 和 b 是字符类型,所以要发生整型提升。

-
printf("%d\n", c);
%d - 10进制的形式打印有符号的整数 , 而c是字符类型,所以再次发生整型提升。

由于这种转换是隐式的,也无法监控到,那如何证明确实有这样的转换呢?
1.
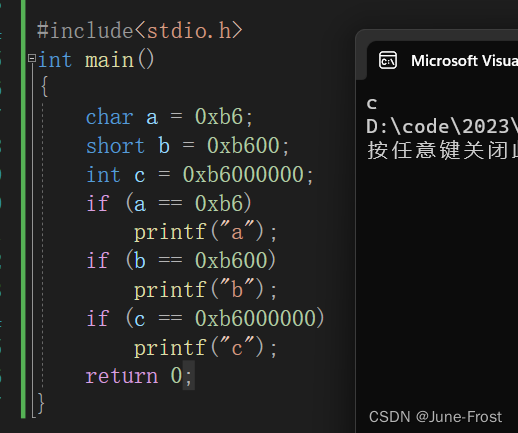
当判断 a == 0xb6 时,a会发生整型提升,由 10110110 变为 11111111 11111111 11111111 10110110 , 本质上 0xb6 是个数值 ,可以看作 00000000 00000000 00000000 10110110 ,这自然是不同的,所以结果是假,b同理,但是c是整型,不需要整型提升,所以表达式 c==0xb6000000 的结果是真 。
2.
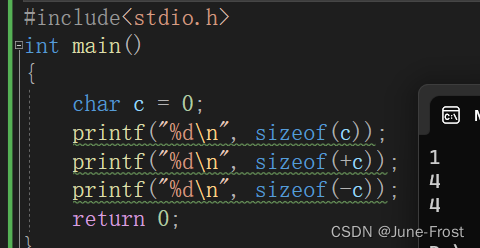
+c 和 -c 参与了表达式运算,发生了整型提升,转化为了普通整型。
通过以上两个例子可以看出,在表达式求解过程中,有着整型提升的参与。
整型提升有两个意义:
1.表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度,同时也是CPU的通用寄存器的长度。因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
2.通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int,然后才能送入CPU去执行算。
当表达式中有char 和 short 时,需要整型提升,当表达式中没有这两个类型,只剩下别的类型时,就会有算术转换的参与。
算术转换
如果某个操作符的各个操作数属于不同的类型,那么除非其中一个操作数的转换为另一个操作数的类型,否则操作就无法进行。下面的层次体系称为寻常算术转换。

例如 :int a = 0; float b = 5.5; 如果要执行 a + b , a 会在计算的时候临时转化为float类型,与 b 相加后得到一个 float 类型的结果。
操作符的属性
复杂表达式的求值有3个影响因素:
1.操作符的优先级;
2.操作符的结合性;
3.是否控制求值顺序;
两个相邻的操作符先执行哪个?取决于他们的优先级。如果两者的优先级相同,取决于他们的结合性。
📙操作符属性表(优先级从上至下)
| 操作符 | 描述 | 用法示例 | 结果类型 | 结合性 | 是否控制求值顺序 |
|---|---|---|---|---|---|
| ( | 聚组 | (表达式) | 与表达式同 | N/A | 否 |
| () | 函数调用 | rexp(rexp,…,rexp) | rexp | L-R | 否 |
| [ ] | 下标引用 | rexp[rexp] | lexp | L-R | 否 |
| . | 访问结构成员 | lexp.member_name | lexp | L-R | 否 |
| -> | 访问结构指针成员 | rexp->member_name | lexp | L-R | 否 |
| ++ | 后缀自增 | lexp ++ | rexp | L-R | 否 |
| – | 后缀自减 | lexp – | rexp | L-R | 否 |
| ! | 逻辑反 | ! rexp | rexp | R-L | 否 |
| + | 单目,表示正值 | + rexp | rexp | R-L | 否 |
| - | 单目 ,表示负值 | - rexp | rexp | R-L | 否 |
| ++ | 前缀自增 | ++ lexp | rexp | R-L | 否 |
| – | 前缀自减 | – lexp | rexp | R-L | 否 |
| * | 间接访问 | * rexp | lexp | R-L | 否 |
| & | 取地址 | & lexp | rexp | R-L | 否 |
| sizeof | 取其长度 , 以字节表示 | sizeof rexp sizeof(类型) | rexp | R-L | 否 |
| (类型) | 类型转换 | (类型) rexp | rexp | R-L | 否 |
| * | 乘法 | rexp * rexp | rexp | L-R | 否 |
| / | 除法 | rexp / rexp | rexp | L-R | 否 |
| % | 整数取余 | rexp % rexp | rexp | L-R | 否 |
| + | 加法 | rexp + rexp | rexp | L-R | 否 |
| - | 减法 | rexp - rexp | rexp | L-R | 否 |
| << | 左移位 | rexp << rexp | rexp | L-R | 否 |
| >> | 右移位 | rexp >> rexp | rexp | L-R | 否 |
| > | 大于 | rexp > rexp | rexp | L-R | 否 |
| >= | 大于等于 | rexp >= rexp | rexp | rexp | 否 |
| < | 小于 | rexp < rexp | rexp | L-R | 否 |
| <= | 小于等于 | rexp <= rexp | rexp | L-R | 否 |
| == | 等于 | rexp == rexp | rexp | L-R | 否 |
| != | 不等于 | rexp != rexp | rexp | L-R | 否 |
| & | 位与 | rexp & rexp | rexp | L-R | 否 |
| ^ | 位异或 | rexp ^ rexp | rexp | L-R | 否 |
| I | 位或 | rexp | rexp | rexp | L-R |
| && | 逻辑与 | rexp && rexp | rexp | L-R | 是 |
| II | 逻辑或 | rexp | rexp | rexp | |
| ? : | 条件操作符 | rexp? rexp : rexp | rexp | N/A | 是 |
| = | 赋值 | lexp = rexp | rexp | R-L | 否 |
| += | 以…加 | lexp += rexp | rexp | R-L | 否 |
| -= | 以…减 | lexp -= rexp | rexp | R-L | 否 |
| *= | 以…乘 | lexp *= rexp | rexp | R-L | 否 |
| /= | 以…除 | lexp /= rexp | rexp | R-L | 否 |
| %= | 以…取模 | lexp %= rexp | rexp | R-L | 否 |
| <<= | 以…左移 | lexp <<= rexp | rexp | R-L | 否 |
| >>= | 以…右移 | lexp >>= rexp | rexp | R-L | 否 |
| &= | 以…与 | lexp &= rexp | rexp | R-L | 否 |
| ^= | 以…异或 | lexp ^= rexp | rexp | R-L | 否 |
| I= | 以…或 | lexp I= rexp | rexp | R-L | 否 |
| , | 逗号 | rexp , rexp | rexp | L-R | 是 |
❗️但是就算操作符有这些属性,也不一定会使得表达式有着唯一的求解路径,例如:
例1:
a* b + c * d + e * f;
两种求解路径:

例2:
int c = 3;
c + --c;
这样的表达式有两种路径:

操作符的优先级只能决定自减–的运算在+的运算的前面,但是我们并没有办法得知,+操作符的左操作数的获取在右操作数之前还是之后,所以结果是不可预测的,是有歧义的。
⚠警告:
表达式如果不能通过操作符的属性确定唯一的计算路径,那这个表达式就是存在问题的。
❤️ 结语
文章到这里就结束了,如果对你有帮助,你的点赞将会是我的最大动力,如果大家有什么问题或者不同的见解,欢迎大家的留言~
相关文章:

【C语言】探讨蕴藏在表达式求解中的因素
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:C语言 🔥该篇将探讨 操作符 和 类型转换 对表达式求解的影响。 目录: 隐式类型转换算术转换操作符的属性❤️ 结语 隐…...

【Flutter】Flutter 使用 video_player 播放视频
【Flutter】Flutter 使用 video_player 播放视频 文章目录 一、前言二、video_player 简介三、安装和配置四、基本使用五、完整示例 六、高级功能七、总结 一、前言 大家好,我是小雨青年,今天我要和大家分享一款非常实用的 Flutter 包——video_player。…...

如何使用 ChatGPT 快速制作播客和其他长篇内容
使用ChatGPT快速制作播客和其他长篇内容是一个高效且具有一定创造性的过程。以下是一些详细的步骤和技巧,以帮助你充分利用ChatGPT来制作高质量的内容。 一、准备阶段 确定主题或话题:在开始制作之前,你需要明确你的播客或长篇内容将聚焦的主…...

JavaScript基础语法02——JS书写位置
哈喽,大家好,我是雷工! 今天继续学习JavaScript基础语法,JS的书写位置,俗话说:好记性不如烂笔头,边学边记,方便回顾。 1、行内JavaScript 代码写在标签内部 示例: <…...

LInux快捷命令
切换到行头:ctrla 或者 ctrlhome 切换到行尾:ctrale 或者 ctrlend 光标向左切换一个单词:ctrl← 光标向右切换一个单词:ctrl→ 历史命令搜索:history 历史命令匹配第一条执行:!x (x表示历史命令…...
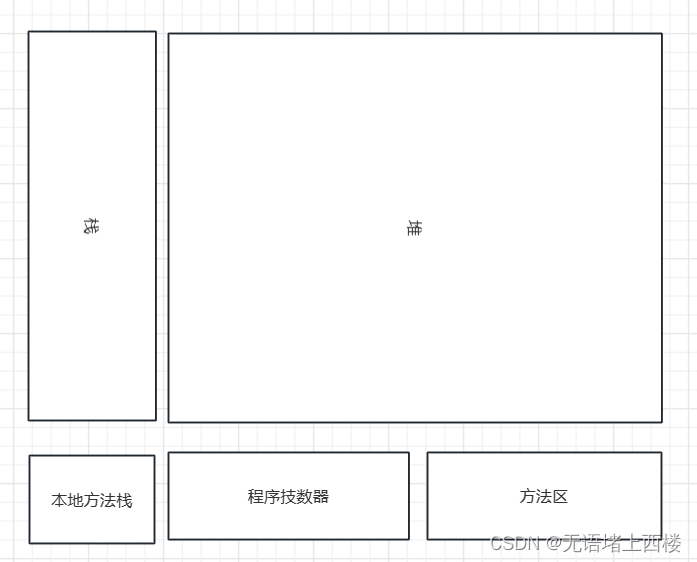
jvm的内存划分区域
jvm划分5个区域: java虚拟机栈、本地方法栈、堆、程序计数器、方法区。 各个区各自的作用: 1.本地方法栈:用于管理本地方法的调用,里面并没有我们写的代码逻辑,其由native修饰,由 C 语言实现。 2.程序计数…...

什么是数据中心IP,优缺点是什么?
如果根据拥有者或者说发送地址来分类的话,可以将代理分为三类:数据中心ip,住宅ip,移动ip 本文我们来了解数据中心ip的原理以及他们的优势劣势,才能选择适合自己的代理。 一、什么是数据中心ip代理? 数据中心ip是由数据中心拥有…...

模块化与组件化:开发中的双剑合璧
引言:模块化与组件化的重要性 在现代软件开发中,随着项目规模的增长和技术的复杂性增加,如何有效地组织和管理代码变得越来越重要。模块化与组件化作为两种主要的代码组织方法,为开发者提供了有效的工具,帮助他们创建…...
【C++初阶】list的常见使用操作
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:C航路 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞…...

排序之插入排序
文章目录 前言一、直接插入排序1、基本思想2、直接插入排序的代码实现3、直接插入排序总结 二、希尔排序1、希尔排序基本思想2、希尔排序的代码实现3、希尔排序时间复杂度 前言 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大…...
c# - - - 安装.net core sdk
如图,安装的是.Net Core 2.2版本 查看安装成功...
Golang Gorm 高级查询之where + find
插入测试数据 package mainimport ("fmt""gorm.io/driver/mysql""gorm.io/gorm" )type Student struct {ID int64Name string gorm:"size:6"Age intEmail *string }func (*Student) TableName() string {return "student&q…...

【LeetCode】30 天 Pandas 挑战
一、笔记 1.对某列进行筛选 df[(df[column1]条件1) | (df[column2]条件2) & (df[column3]条件3)][[columns]]真题: (一)条件筛选——1.大的国家(一)条件筛选——2.可回收且低脂的产品(一)…...

头歌MYSQL——课后作业2 数据表中数据的插入、修改和删除
第1关:数据表中插入一条记录,对指定字段赋值 任务描述 本关任务:在library数据库的reader数据表中插入一条数据 姓名xm为林团团,电话号码dhhm为13507311234,其余字段取默认值 显示数据表的所有数据 为了完成本关任务,…...

Maven的profiles多环境配置
一个项目通常都会有多个不同的运行环境,例如开发环境,测试环境、生产环境等。而不同环境的构建过程很可能是不同的,例如数据源配置、插件、以及依赖的版本等。每次将项目部署到不同的环境时,都需要修改相应的配置,这样…...

go 协程
golang中的并发是函数相互独立运行的能力。Goroutines是并发运行的函数。Golang提供了 如何实现go协程 只需要在函数前面加上go即可 go task()package mainimport ("fmt""time" )func show(msg string) {for i : 0; i < 5; i {fmt.Printf("msg: …...
【python爬虫案例】用python爬豆瓣读书TOP250排行榜!
文章目录 一、爬虫对象-豆瓣读书TOP250二、python爬虫代码讲解三、讲解视频四、完整源码 一、爬虫对象-豆瓣读书TOP250 您好,我是 马哥python说 ,一名10年程序猿。 今天我们分享一期python爬虫案例讲解。爬取对象是,豆瓣读书TOP250排行榜数…...

Qt中 gui 模块和 widgets 模块的区别
1. gui 模块提供了基本的图形系统抽象层,包括QPaintDevice、QPainter等类,这些类构成了Qt的绘图基础。 2. widgets 模块在 gui 模块的基础上,提供了完整的桌面级用户界面控件,如按钮、列表、滑块等。这些控件继承自更基础的图形类。 3. gui 模块是更底层的图形功能,widgets模…...
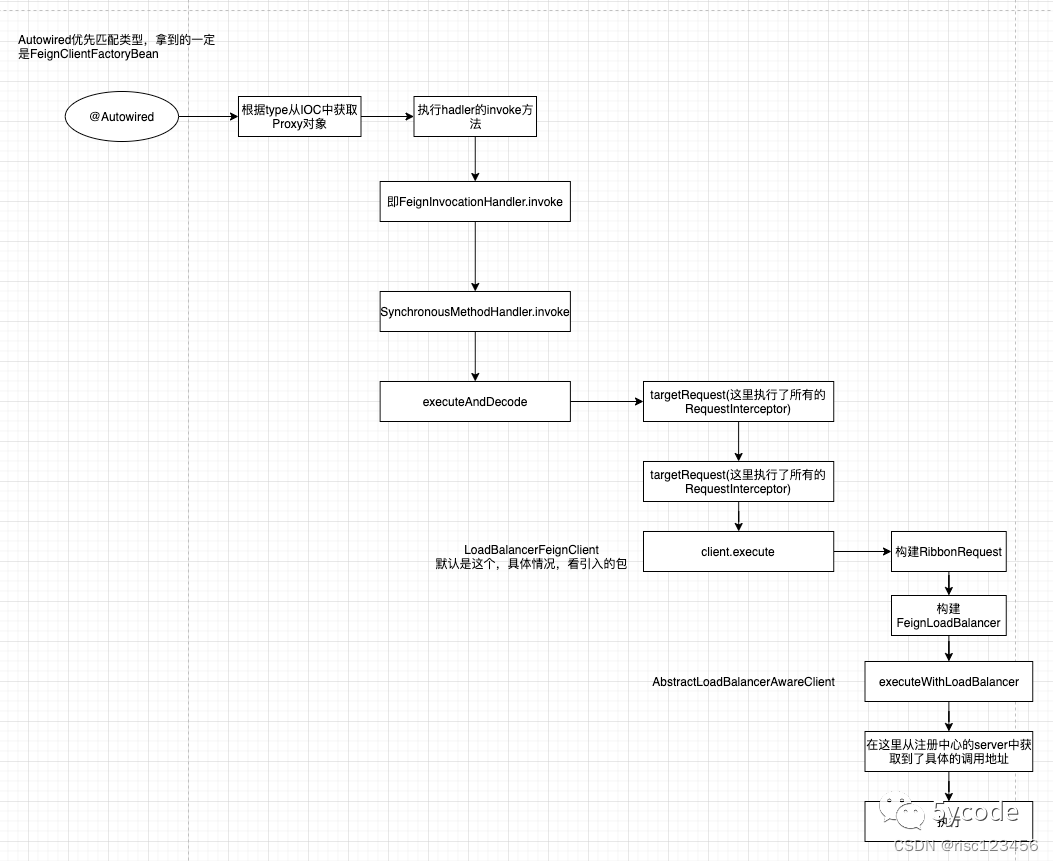
feign调用流程
...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

