代码随想录打卡—day52—【子序列问题】— 8.31 最大子序列
共性
做完下面三题,发现三个的dp数组中i都是以 i 为结束的字串。
1 300. 最长递增子序列
300. 最长递增子序列
AC:
class Solution {
public:int dp[10010]; // 表示以i结束的子序列最大的长度/*if(nums[j] > nums[i])dp[j] = max(dp[j],dp[i] + 1);dp[0..nums.size()-1] = 1;每个i结束i++ , j = 0...n-1 j++模拟——*/int lengthOfLIS(vector<int>& nums) {for(int i = 0; i < nums.size();i++)dp[i] = 1;int ans = 0;for(int i = 0; i < nums.size();i++){for(int j = 0; j < i; j++){if(nums[j] < nums[i])dp[i] = max(dp[i],dp[j] + 1);}ans = max(ans,dp[i]);}return ans;}
};2 674. 最长连续递增序列
674. 最长连续递增序列
和上一题差不多,就是 j 直接为 i - 1 即可。AC代码:
class Solution {
public:int dp[10010]; // 以i结束的子序列最长的连续递增的长度/*j = i-1if(nums[i] > nums[j])dp[i] = max(dp[i],dp[j])dp[0...n-1] = 1i++ j模拟——*/int findLengthOfLCIS(vector<int>& nums) {for(int i = 0; i < nums.size();i++)dp[i] = 1;int ans = 1;for(int i = 1; i < nums.size();i++){int j = i-1;if(nums[i] > nums[j])dp[i] = max(dp[i],dp[j]+1);ans = max(ans,dp[i]);cout << dp[i] << ' ';}return ans;}
};前两题概括来说:
不连续递增子序列的跟前0-i 个状态有关,连续递增的子序列只跟前一个状态有关
3 718. 最长重复子数组
718. 最长重复子数组
重点:
1.
注意题目中说的子数组,暗指的是连续子序列。
2.
int dp[1010][1010]; // nums1以i结尾! nums2的以j结尾! 最长公共子串的长度
以x结尾两个字串才可比较。
3.
需要重点理解dp[i][j] 只能从dp[i-1][j-1]推导出来 不能从dp[i-1][j] 或是dp[i][j-1]
carl一共在实现细节上给了三种方式,我使用了dp数组含义更加直观但是多写几行的第三种写法(在拓展部分)AC代码:
class Solution {
public:int dp[1010][1010]; // nums1以i结尾! nums2的以j结尾! 最长公共子串的长度/*需要重点理解dp[i][j] 只能从dp[i-1][j-1]推导出来 不能从dp[i-1][j] 或是dp[i][j-1]if(nums[i] == nums[j])dp[i][j] = dp[i - 1][j - 1] + 1else dp[i][j] = 0for(int j = 0; j < nums1.size();j++)if(nums2[0] == nums1[i]) dp[0][j] = 1else dp[0][j] = 0for(int i = 0; i < nums2.size();i++)if(nums1[0] == nums2[i]) dp[i][0] = 1else dp[i][0] = 0;i++ j++*/int findLength(vector<int>& nums1, vector<int>& nums2) {int ans = 0;for(int j = 0; j < nums1.size();j++){if(nums2[0] == nums1[j]) dp[0][j] = 1;else dp[0][j] = 0;ans = max(ans,dp[0][j]);}for(int i = 0; i < nums2.size();i++){if(nums1[0] == nums2[i]) dp[i][0] = 1;else dp[i][0] = 0;ans = max(ans,dp[i][0]);}for(int i = 1; i < nums2.size();i++){for(int j = 1; j < nums1.size();j++){if(nums2[i] == nums1[j])dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = 0;ans = max(ans,dp[i][j]);}}// for(int i = 0; i < nums2.size();i++)// {// for(int j = 0; j < nums1.size();j++)// cout << dp[i][j] << ' ';// cout << endl;// }return ans;}
};相关文章:

代码随想录打卡—day52—【子序列问题】— 8.31 最大子序列
共性 做完下面三题,发现三个的dp数组中i都是以 i 为结束的字串。 1 300. 最长递增子序列 300. 最长递增子序列 AC: class Solution { public:int dp[10010]; // 表示以i结束的子序列最大的长度/*if(nums[j] > nums[i])dp[j] max(dp[j],dp[i] …...

gcc4.8.5升级到gcc4.9.2
第1步:获取repo [rootlocalhost SPECS]# wget --no-check-certificate https://copr.fedoraproject.org/coprs/rhscl/devtoolset-3/repo/epel-6/rhscl-devtoolset-3-epel-6.repo -O /etc/yum.repos.d/devtoolset-3.repo --2021-12-07 20:53:26-- https://copr.fedo…...
:常用函数)
Golang 中的 archive/zip 包详解(三):常用函数
Golang 中的 archive/zip 包用于处理 ZIP 格式的压缩文件,提供了一系列用于创建、读取和解压缩 ZIP 格式文件的函数和类型,使用起来非常方便,本文讲解下常用函数。 zip.OpenReader 定义如下: func OpenReader(name string) (*R…...

微服务架构七种模式
微服务架构七种模式 目录概述需求: 设计思路实现思路分析 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,challenge Survive.…...
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm...
关于CICD流水线的前端项目运行错误,npm项目环境配置时出现报错:Not Found - GET https://registry.npm… 原因应该是某些jar包缓存中没有需要改变镜像将包拉下来 npm config set registry http://registry.npm.taobao.org npm install npm run build...

element-plus的周选择器 一周从周一开始
1、代码 1)、template中 <el-date-picker v-model"value1" type"week" format"[Week] ww" placeholder"巡访周" change"change"value-format"YYYY-MM-DD" /> 2)、方法中 import…...

Android 9.0 pms获取应用列表时过滤掉某些app功能实现
1.前言 在9.0的系统rom定制化开发中,对系统定制的功能也是很多的,在一次产品开发中,要求在第三方app获取应用列表的时候,需要过滤掉某些app,就是不显示在app应用列表中,这就需要在pms查询app列表时过滤掉这些app就可以了,接下来就实现这些功能 2.pms获取应用列表时过滤掉…...

HTML <thead> 标签
实例 带有 thead、tbody 以及 tfoot 元素的 HTML 表格: <table border="1"><thead><tr><th>Month</th><th>Savings</th></tr></thead><tfoot><tr><td>Sum</td><td>$180<…...

谷歌发布Gemini以5倍速击败GPT-4
在Covid疫情爆发之前,谷歌发布了MEENA模型,短时间内成为世界上最好的大型语言模型。谷歌发布的博客和论文非常可爱,因为它特别与OpenAI进行了比较。 相比于现有的最先进生成模型OpenAI GPT-2,MEENA的模型容量增加了1.7倍…...
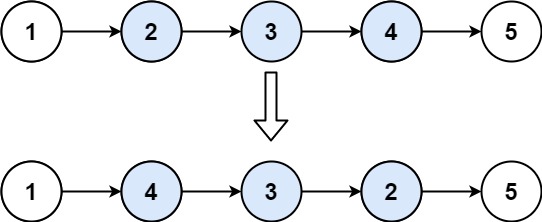
力扣92. 局部反转链表
92. 反转链表 II 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。 示例 1: 输入:head [1,2,3,4,5], left 2, right 4 输出&am…...

九、适配器模式
一、什么是适配器模式 适配器模式(Adapter)的定义如下:将一个类的接口转换成客户希望的另外一个接口,使得原本由于接口不兼容而不能一起工作的那些类能一起工作。 适配器模式(Adapter)包含以下主要角色&…...
使用spring自带的发布订阅来实现发布订阅
背景 公司的项目以前代码里面有存在使用spring自带发布订阅的代码,因此稍微学习一下如何使用,并了解一下这种实现方式的优缺点。 优点 实现方便,代码方面基本只需要定义消息体和消费者,适用于小型应用程序。不依赖外部中间件&a…...
Walmart电商促销活动即将开始,如何做促销活动?需要注意什么?
近日,沃尔玛官宣Baby Days优惠活动将于9月1日正式开始!卖家可以把握机会,通过设置促销定价,以最优惠的婴儿相关产品价格吸引消费者,包括汽车座椅、婴儿车、尿布袋、家具、床上用品、消耗品、婴儿服装、孕妇装等。注意本…...
Matlab(画图进阶)
目录 大纲 1.特殊的Plots 1.1 loglog(双对数刻度图) 1.3 plotyy(创建具有两个y轴的图形) 1.4yyaxis(创建具有两个y轴的图) 1.5 bar 3D条形图(bar3) 1.6 pie(饼图) 3D饼图 1.7 polar 2.Stairs And Ste阶梯图 3.Boxplot 箱型图和Error Bar误差条形图 3.1 boxplot 3.2 …...

人生的回忆
回忆是人类宝贵的精神财富,它们像一串串珍珠,串联起我们生活中的每一个片段。 回忆是时间的见证者,它们承载着我们成长、经历、悲欢离合的点点滴滴。 回忆让我们重温过去的欢笑与眼泪,感受那些已经逝去的时光。它们就像一本翻开的…...

Spring之依赖注入源码解析
Spring之依赖注入源码解析 Spring依赖注入的方式 手动注入 在XML中定义Bean时,即为手动注入,因为是程序员手动给某个属性指定了值。 通过set方式进行注入 <bean name"userService" class"com.luban.service.UserService">…...
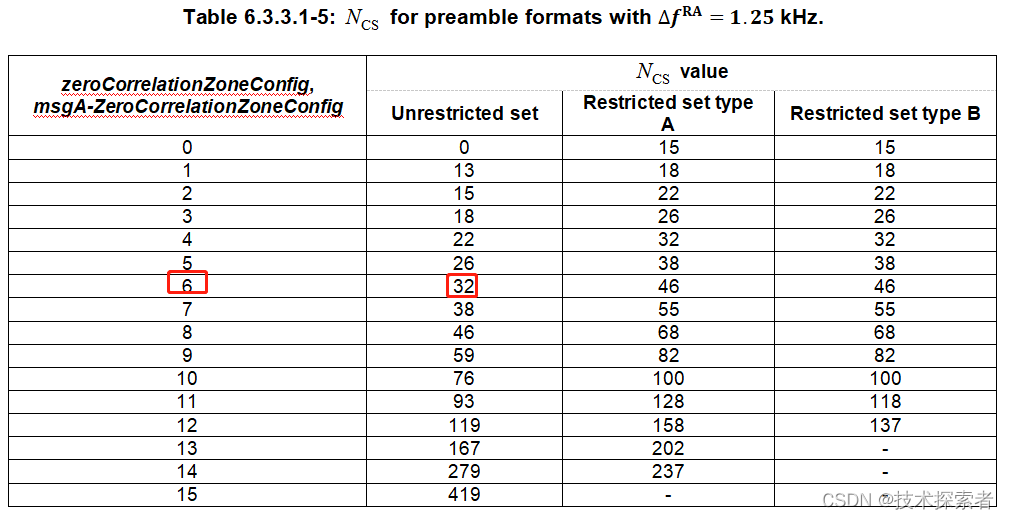
5G NR:RACH流程-- Msg1之生成PRACH Preamble
随机接入流程中的Msg1,即在PRACH信道上发送random access preamble。涉及到两个问题: 一个是如何产生preamble?一个是如何选择正确的PRACH时频资源发送所选的preamble? 一、PRACH Preamble是什么 PRACH Preamble从数学上来讲是一个长度为…...
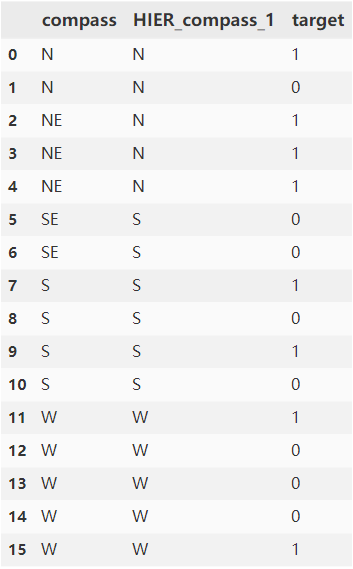
高基数类别特征预处理:平均数编码 | 京东云技术团队
一 前言 对于一个类别特征,如果这个特征的取值非常多,则称它为高基数(high-cardinality)类别特征。在深度学习场景中,对于类别特征我们一般采用Embedding的方式,通过预训练或直接训练的方式将类别特征值编…...

高效利用隧道代理实现无阻塞数据采集
在当今信息时代,大量的有价值数据分散于各个网站和平台。然而,许多网站对爬虫程序进行限制或封禁,使得传统方式下的数据采集变得困难重重。本文将向您介绍如何通过使用隧道代理来解决这一问题,并帮助您成为一名高效、顺畅的数据采…...

图论岛屿问题DFS+BFS
leetcode 200 岛屿问题 class Solution {//定义对应的方向boolean [][] visited;int dir[][]{{0,1},{1,0},{-1,0},{0,-1}};public int numIslands(char[][] grid) {//对应的二维数组int count0;visitednew boolean[grid.length][grid[0].length];for (int i 0; i < grid.l…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
