面试必备:揭秘ArrayList和LinkedList,区别、优缺点与使用场景
大家好,我是你们的小米!今天我要跟大家聊一个在面试中经常被问到的热门话题——ArrayList和LinkedList的区别、优缺点以及它们的使用场景。作为程序员,掌握这些知识点不仅可以在面试中脱颖而出,还能帮助我们更好地在项目中选择合适的数据结构,提升代码效率和性能。废话不多说,让我们开始吧!
ArrayList和LinkedList是什么?
在介绍它们的区别之前,我们先来了解一下ArrayList和LinkedList分别是什么。
- ArrayList: ArrayList是Java集合框架中的一个类,它实现了List接口,底层基于数组实现。ArrayList的特点是支持动态数组,可以自动扩容,适合顺序访问和随机访问。
- LinkedList: LinkedList也是Java集合框架中的一个类,同样实现了List接口,但底层基于链表实现。LinkedList的特点是支持高效的插入和删除操作,但随机访问的性能相对较差。
区别与优缺点对比
- 存储结构:ArrayList使用数组作为底层数据结构,数据在内存中是连续存储的,因此支持随机访问非常快速。LinkedList则使用链表作为底层数据结构,每个元素都包含指向前后元素的指针,插入和删除操作非常高效。
- 插入与删除操作:在ArrayList中,如果插入或删除元素,可能会导致数组元素的移动,从而影响性能。而LinkedList在插入和删除操作上具有明显优势,因为只需修改指针的指向,不需要移动大量元素。
- 随机访问性能:由于ArrayList的数组连续存储特性,它在随机访问上具有很好的性能。通过索引即可直接访问元素。而LinkedList需要从头或尾开始遍历链表,随机访问性能较差。
- 内存占用:由于LinkedList每个元素都需要存储前后指针,相对于ArrayList会占用更多的内存空间。如果需要存储大量数据,考虑内存占用也是一个重要因素。
- 迭代性能:在迭代(遍历)操作上,ArrayList由于连续存储的特性,性能通常较好。而LinkedList在迭代操作上由于需要通过指针跳转,性能相对较差。
如何选择?
那么在实际开发中,我们如何选择ArrayList还是LinkedList呢?下面我会为大家总结一些使用场景,帮助大家更好地做出决策。
使用ArrayList的场景:
- 需要频繁进行随机访问,例如根据索引获取元素。
- 数据集合相对固定,不需要频繁的插入和删除操作。
- 内存占用相对较少,不会造成严重的资源浪费。
使用LinkedList的场景:
- 需要频繁进行插入和删除操作,尤其是在中间位置。
- 不关心随机访问性能,而更关注插入和删除的效率。
- 可能需要更少的内存占用,尤其是在元素数量较少的情况下。
END
通过本文,我们了解了ArrayList和LinkedList的区别、优缺点以及使用场景。在面试中,当被问到这个问题时,我们可以根据实际情况进行分析,选择更合适的数据结构来解决问题。同时,也要根据项目的实际需求来权衡性能和资源占用,做出明智的选择。
希望本文对大家理解ArrayList和LinkedList有所帮助!如果你觉得这篇文章不错,记得点赞和分享给更多的小伙伴哦!感谢大家的支持,我们下期再见~
如有疑问或者更多的技术分享,欢迎关注我的微信公众号“知其然亦知其所以然”!

相关文章:

面试必备:揭秘ArrayList和LinkedList,区别、优缺点与使用场景
大家好,我是你们的小米!今天我要跟大家聊一个在面试中经常被问到的热门话题——ArrayList和LinkedList的区别、优缺点以及它们的使用场景。作为程序员,掌握这些知识点不仅可以在面试中脱颖而出,还能帮助我们更好地在项目中选择合适…...
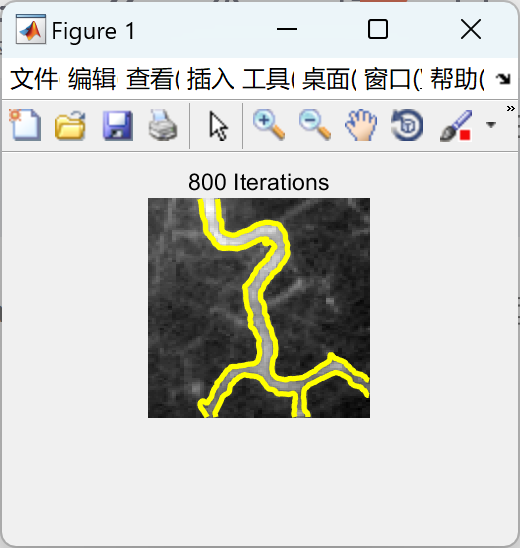
【局部活动轮廓】使用水平集方法实现局部活动轮廓方法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Git 同步远程新的同名分支
背景 因为远程分支的提交记录过多,导致本地的commit内容过大,会产生一些问题: 第一次拉取时间较长占用本地和远程的存储 原因 因为项目已有一些年头,若是每次文件提交比较大,那么占用空间就更大 解决方案 该方案…...

PingCode DevOps 团队:企业CICD流水线可能会遇到的问题及解法
CICD 流水线是指一系列自动化的构建、测试和部署步骤,用于将应用程序从开发到生产环境的过程。在 CICD 流水线中,每个步骤都是自动化的,并且在完成后会触发下一个步骤的执行。 CICD 的价值 CICD 流水线可以帮助团队更快地交付产品ÿ…...
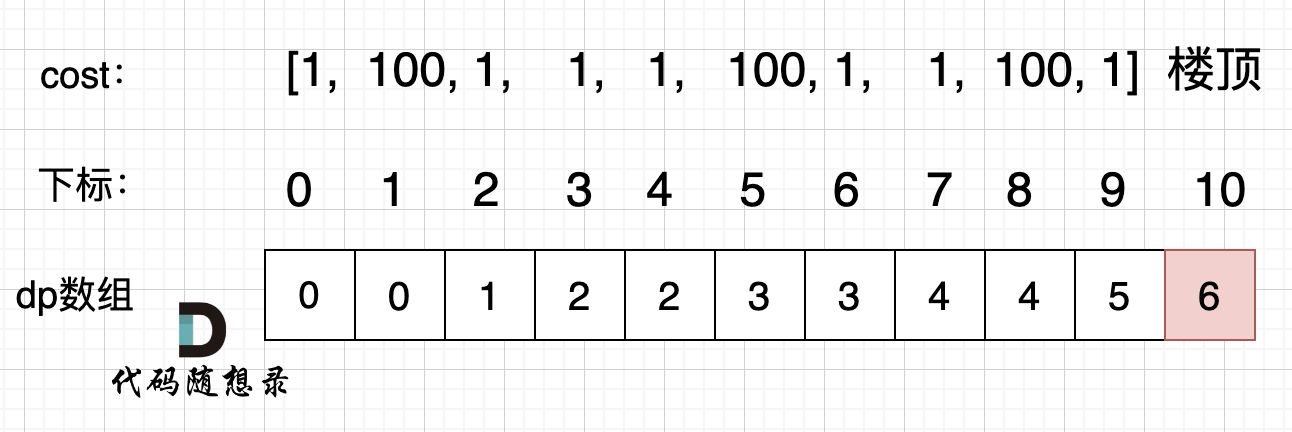
【LeetCode题目详解】第九章 动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯 (day38补)
本文章代码以c为例! 一、力扣第509题:斐波那契数 题目: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:…...
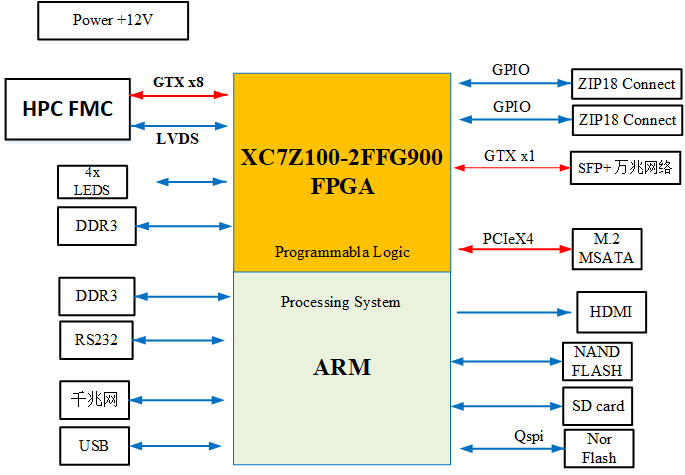
图像处理 信号处理板 设计原理图:367-基于zynq XC7Z100 FMC接口通用计算平台
基于zynq XC7Z100 FMC接口通用计算平台 一、板卡概述 板卡由SoC XC7Z100-2FFG900I芯片来完成卡主控及数字信号处理,XC7Z100内部集成了两个ARM Cortex-A9核和一个kintex 7的FPGA,通过PL端FPGA扩展FMC、光纤、IO等接口,PS端ARM扩展网络、USB、R…...
的七种用法)
PHP中header()的七种用法
我们在实际开发中经常使用header()实现一些功能,这篇文章介绍关于header()的7中用法,需要的伙伴的开参考一下。 PHP header()的7中用法: 1、跳转页面 可以使用header()实现跳转页面功能。 header(Location:.$url); // $url 跳转页面的地址…...

臻图信息以数字孪生技术推动智慧小区数字化建设
伴随着智慧城市建设进程的加速发展,加速传统小区的管理与服务向智能化升级转型。运用智慧化的管理和服务,利用信息技术和物联网等技术手段,将传统的居住区域与智能设备相结合,实现楼宇、社区设施、服务管理的数字化、网络化、智能…...

15.CSS发光按钮的悬停特效
效果 源码 <!DOCTYPE html> <html> <head><title>CSS Modern Button</title><link rel="stylesheet" type="text/css" href="style.css"> </head> <body><a href="#" style=&quo…...

MyBatis —— 动态SQL和缓存
前言 在上一篇文章中荔枝梳理了一些特殊的SQL查询和一对多、多对一的映射关系,而在这篇文章中荔枝将会梳理有关MyBatis动态SQL和MyBatis缓存的相关知识,同时也稍微了解了有关MyBatis中借助MAVEN中的插件管理来实现逆向工程。希望对需要的小伙伴有帮助哈哈…...
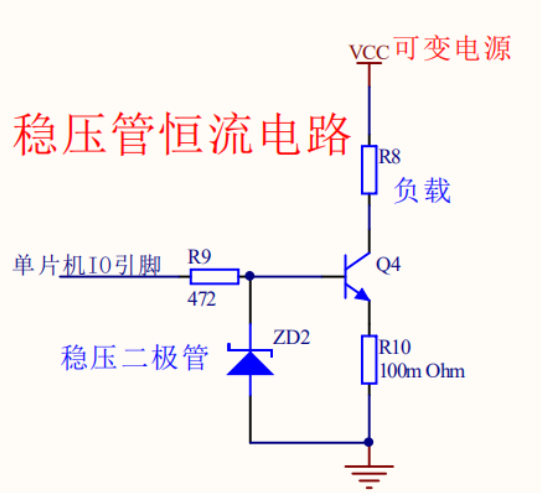
恒流电路的三种设计方案
作为硬件研发工程师相信对恒流电路不会陌生,本文介绍下三种恒流电路的原理图。 三极管恒流电路 三极管恒流电路 三极管的恒流电路,主要是利用Q2三极管的基级导通电压为0.6~0.7V这个特性;当Q2三极管导通,Q1三极管基级电压被拉低而…...

QT基础 关于QT延迟
目录 QT提供延时 1.自定义延时 2.使用QElapsedTimer 3.使用事件循环 4.跨平台延时 QT提供延时 这里提供四种方法: 1、多线程程序使用QThread::sleep()或者QThread::msleep()或QThread::usleep()或QThread::wait()进行延时处理。 Sleep不会释放对象锁&#x…...

LLM - LLaMA-2 获取文本向量并计算 Cos 相似度
目录 一.引言 二.获取文本向量 1.hidden_states 与 last_hidden_states ◆ hidden_states ◆ last_hidden_states 2.LLaMA-2 获取 hidden_states ◆ model config ◆ get Embedding 三.获取向量 Cos 相似度 1.向量选择 2.Cos 相似度 3.BERT-whitening 特征白化 …...

【创建型设计模式】C#设计模式之工厂模式,以及通过反射实现动态工厂。
题目如下: 假设你正在为一家汽车制造公司编写软件。公司生产多种类型的汽车,包括轿车、SUV和卡车。每种汽车都有不同的特点和功能。请设计一个工厂模式,用于创建不同类型的汽车对象。该工厂模式应具有以下要求:工厂类名为 CarFac…...
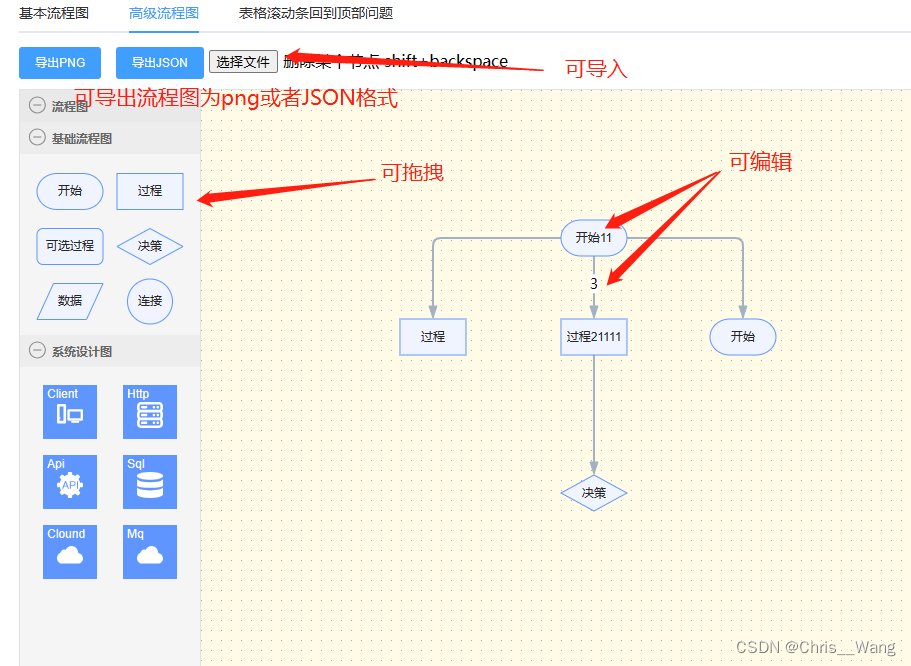
可拖拽编辑的流程图X6
先上图 //index.html,有时候可能加载失败,那就再找一个别的cdn 或者npm下载,如果npm下载, //那么需要全局引入或者局部引入,代码里面写法也会不同,详细的可以看示例<script src"https://cdn.jsdeli…...

神经网络与卷积神经网络
全连接神经网络 概念及应用场景 全连接神经网络是一种深度学习模型,也被称为多层感知机(MLP)。它由多个神经元组成的层级结构,每个神经元都与前一层的所有神经元相连,它们之间的连接权重是可训练的。每个神经元都计算…...

《Java极简设计模式》第05章:原型模式(Prototype)
作者:冰河 星球:http://m6z.cn/6aeFbs 博客:https://binghe.gitcode.host 文章汇总:https://binghe.gitcode.host/md/all/all.html 源码地址:https://github.com/binghe001/java-simple-design-patterns/tree/master/j…...

OceanBase 4.1解读:读写兼备的DBLink让数据共享“零距离”
梁长青,OceanBase 高级研发工程师,从事 SQL 执行引擎相关工作,目前主要负责 DBLink、单机引擎优化等方面工作。 沈大川,OceanBase 高级研发工程师,从事 SQL 执行引擎相关工作,曾参与 TPC-H 项目攻坚&#x…...
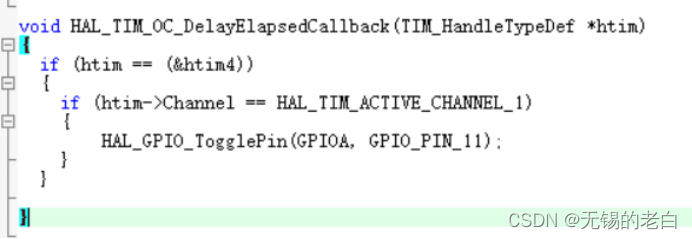
STM32的HAL库的定时器使用
用HAL库老是忘记了定时器中断怎么配置,该调用哪个回调函数。今天记录一下,下次再忘了就来翻一下。 系统的时钟配置,定时器的时钟是84MHz 这里定时器时钟是84M,分频是8400后,时基就是1/10000s,即0.1ms。Per…...
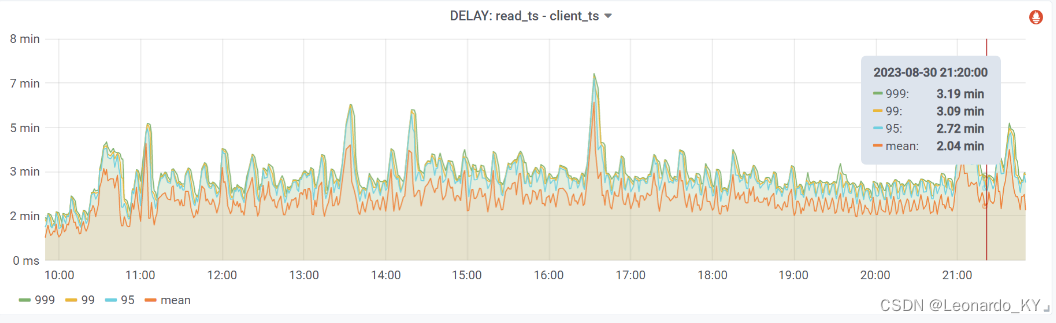
Flink+Paimon多流拼接性能优化实战
目录 (零)本文简介 (一)背景 (二)探索梳理过程 (三)源码改造 (四)修改效果 1、JOB状态 2、Level5的dataFile总大小 3、数据延迟 (五&…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
