Unity中的数学基础——贝塞尔曲线
一:前言
一条贝塞尔曲线是由一组定义的控制点P0到 Pn,n=1为线性,n=2为二次......第一个和最后一个控制点称为起点和终点,中间的控制点一般不会位于曲线上
获取两个点之间的点就是通过线性插值( Mathf.Lerp),0 <= t <= 1
二:贝塞尔曲线公式
——线性公式:给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。这条线由下式给出
![]()
——二阶贝塞尔曲线:二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B(t)公式推导:由(P0,P1),(P1,P2)分别求线性公式所得的结果P0‘ 和 P1‘再带入线性公式,整理所得即为二次公式
P0,P1所求:![]()
P1,P2所求:![]()
P0,P1,P2二次方公式: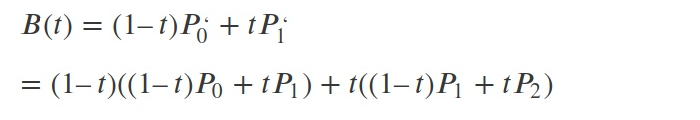
简化所得![]()
——三阶贝塞尔曲线:P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
其公式为![]()
三:公式转换为代码
using UnityEngine;/// <summary>
/// 贝塞尔工具类
/// </summary>
public static class BezierUtils
{/// <summary>/// 线性贝塞尔曲线/// </summary>public static Vector3 BezierCurve(Vector3 p0, Vector3 p1, float t){Vector3 B = Vector3.zero;B = (1 - t) * p0 + t * p1;return B;}/// <summary>/// 二阶贝塞尔曲线/// </summary>public static Vector3 BezierCurve(Vector3 p0, Vector3 p1, Vector3 p2, float t){Vector3 B = Vector3.zero;float t1 = (1 - t) * (1 - t);float t2 = 2 * t * (1 - t);float t3 = t * t;B = t1 * p0 + t2 * p1 + t3 * p2;return B;}/// <summary>/// 三阶贝塞尔曲线/// </summary>public static Vector3 BezierCurve(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t){Vector3 B = Vector3.zero;float t1 = (1 - t) * (1 - t) * (1 - t);float t2 = 3 * t * (1 - t) * (1 - t);float t3 = 3 * t * t * (1 - t);float t4 = t * t * t;B = t1 * p0 + t2 * p1 + t3 * p2 + t4 * p3;return B;}
}四:绘制出曲线
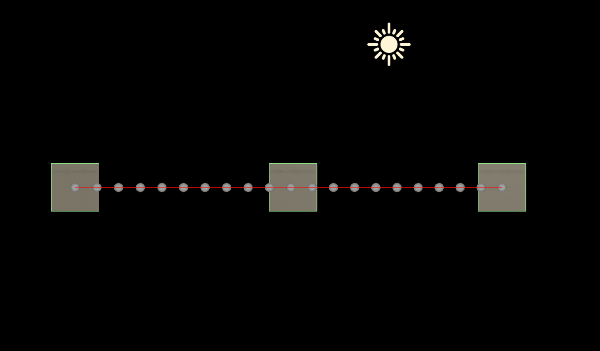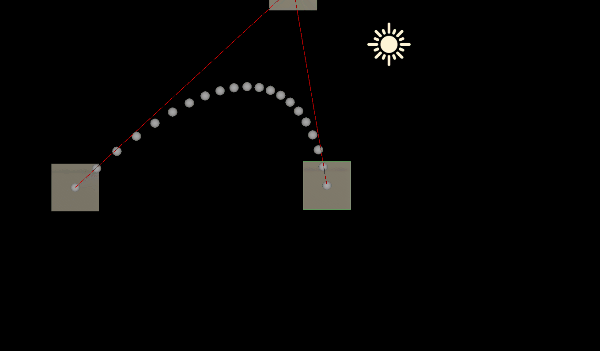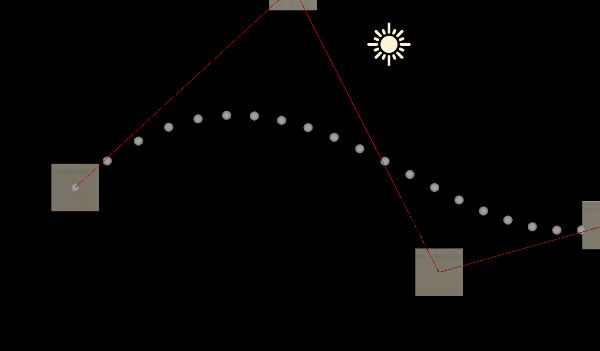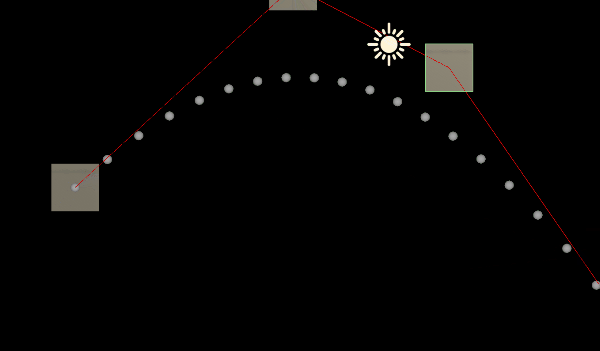
using System.Collections.Generic;
using UnityEngine;public class BezierTest : MonoBehaviour
{public int m_CurveDensity;//曲线密度public bool m_IsSecondOrderBezier;//是否为二阶贝塞尔曲线,否则为三阶贝塞尔曲线private List<Transform> m_ControlPointList = new List<Transform>();//所有的控制点(控制点作为挂载此脚本的游戏物体的子物体)public void OnDrawGizmos(){//添加控制点m_ControlPointList.Clear();foreach (Transform trans in transform){m_ControlPointList.Add(trans);}List<Vector3> pointList = new List<Vector3>();//曲线上的所有点if (m_IsSecondOrderBezier){if (m_ControlPointList.Count < 3){return;}//获取曲线上的所有点for (int i = 0; i < m_ControlPointList.Count - 2; i += 2){Vector3 p0 = m_ControlPointList[i].position;Vector3 p1 = m_ControlPointList[i + 1].position;Vector3 p2 = m_ControlPointList[i + 2].position;for (int j = 0; j <= m_CurveDensity; j++){float t = j * 1f / m_CurveDensity;Vector3 point = BezierUtils.BezierCurve(p0, p1, p2, t);pointList.Add(point);}}}else{if (m_ControlPointList.Count < 4){return;}//获取曲线上的所有点for (int i = 0; i < m_ControlPointList.Count - 3; i += 3){Vector3 p0 = m_ControlPointList[i].position;Vector3 p1 = m_ControlPointList[i + 1].position;Vector3 p2 = m_ControlPointList[i + 2].position;Vector3 p3 = m_ControlPointList[i + 3].position;for (int j = 0; j <= m_CurveDensity; j++){float t = j * 1f / m_CurveDensity;Vector3 point = BezierUtils.BezierCurve(p0, p1, p2, p3, t);pointList.Add(point);}}}//绘制所有点foreach (var point in pointList){Gizmos.DrawSphere(point, 0.1f);}//绘制控制点连线Gizmos.color = Color.red;for (int i = 0; i < m_ControlPointList.Count - 1; i++){Gizmos.DrawLine(m_ControlPointList[i].position, m_ControlPointList[i + 1].position);}}
}相关文章:

Unity中的数学基础——贝塞尔曲线
一:前言 一条贝塞尔曲线是由一组定义的控制点P0到 Pn,n1为线性,n2为二次......第一个和最后一个控制点称为起点和终点,中间的控制点一般不会位于曲线上 获取两个点之间的点就是通过线性插值( Mathf.Lerp)…...

大数据平台安全主要是指什么安全?如何保障?
大数据时代已经来临,各种数据充斥着我们的生活与工作。随着数据的多样性以及复杂性以及大量性,大数据平台诞生了。但对于大数据平台大家都不是很了解,有人问大数据平台安全主要是指什么安全?如何保障? 大数据平台安全…...
Flutter的未来与趋势,23年还学吗?
随着移动应用市场的不断扩大,跨平台开发框架的需求也越来越大。Flutter框架可以帮助开发者在不同平台上快速开发高质量的移动应用程序,这种趋势将进一步推动Flutter的发展和普及。 作为一名前端开发工程师,学习Flutter框架是非常有必要的。因…...
RHCE——十三、Shell自动化运维编程基础
Shell 一、为什么学习和使用Shell编程二、Shell是什么1、shell起源2、查看当前系统支持的shell3、查看当前系统默认shell4、Shell 概念 三、Shell 程序设计语言1、Shell 也是一种脚本语言2、用途 四、如何学好shell1、熟练掌握shell编程基础知识2、建议 五、Shell脚本的基本元素…...

深入理解AMBA总线协议(AXI总结篇)
AXI总线已经是AMBA总线中最常见,使用最频繁的总线,并且没有之一。 可以说AXI总线已经成为了片上总线中最重要的协议,本篇文章打算花一些篇幅,帮大家总结一下AXI总线的学习重点、学习难点,以帮助大家更好更快的掌握AXI…...
)
建立无需build的react单页面应用SPA框架(2)
react-18.1.0,rc-easyui-1.2.9,babel-7.17.11 SPA还要处理的问题: (一)tabs切换事件通知 tabs切换时,自己的框架需要处理组件的生命周期,要有active/deactive,让组件能知道何时创…...
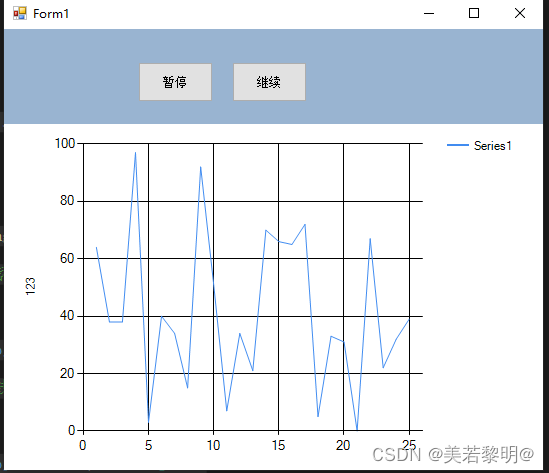
C# char曲线控件
一、char曲线显示随机数数据 using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Runtime.InteropServices; using System.Text; using System.Threading; using Syst…...

远程访问本地jupyter notebook服务 - 无公网IP端口映射
文章目录 前言1. Python环境安装2. Jupyter 安装3. 启动Jupyter Notebook4. 远程访问4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5. 固定公网地址 前言 Jupyter Notebook,它是一个交互式的数据科学和计算环境,支持多种编程语言,如…...

flume系列之:记录一次消费大量Debezium数据,数据包含dml语句比较大,造成数据堆积在channel的解决方法
flume系列之:记录一次消费大量Debezium数据,数据包含dml语句比较大,造成数据堆积在channel的解决方法 一、背景二、相关技术博客三、flume层面解决方法四、debezium数据采集层面解决方法一、背景 Debezium采集了大量的数据,数据包含DMl语句,数据本身比较大。flume消费了大…...

Could not find artifact com.pageOffice:pageOffice:pom:4.3.0.2 in aliyunmaven
Could not find artifact com.pageOffice:pageOffice:pom:4.3.0.2 in aliyunmaven (https://maven.aliyun.com/repository/public) 仓库服务 阿里云云效 Maven 是什么 阿里云Maven中央仓库为 阿里云云效 提供的公共代理仓库,帮助研发人员提高研发生产效率&#x…...

2023年9月数据治理/项目管理/产品管理/商务礼仪企业内训定制
在节奏飞驰、风起云涌的企业世界中,为了企业的蓬勃发展,可以在内部或者外部挑选有经验的老师进行培训和学习。简而言之,任何一个企业想要发展,都少不了进行内训。 企业内训的好处 提高员工的技能和知识水平 通过不断地学习和培训…...

后端面试话术集锦第 九 篇:Activiti工作流面试话术
这是后端面试集锦第九篇博文——Activiti工作流面试话术❗❗❗ 1. 工作流话术 工作流这块儿,实际在工作中使用的时候,Activiti用的居多,当然还有一些其他的工作流引擎。 在网上看了也大概看了一下,其他的像JBPM以及workflow等用的情况来讲不是很多。 所以说Activiti目前…...

JS中方法、函数、属性是一个东西吗
在 JavaScript 中,方法、函数和属性是相关但不完全相同的概念。 方法(Method):在对象中,方法是对象的属性,但它的值是一个函数。方法可以通过对象来调用,并且可以访问对象的属性和其他方法。 …...
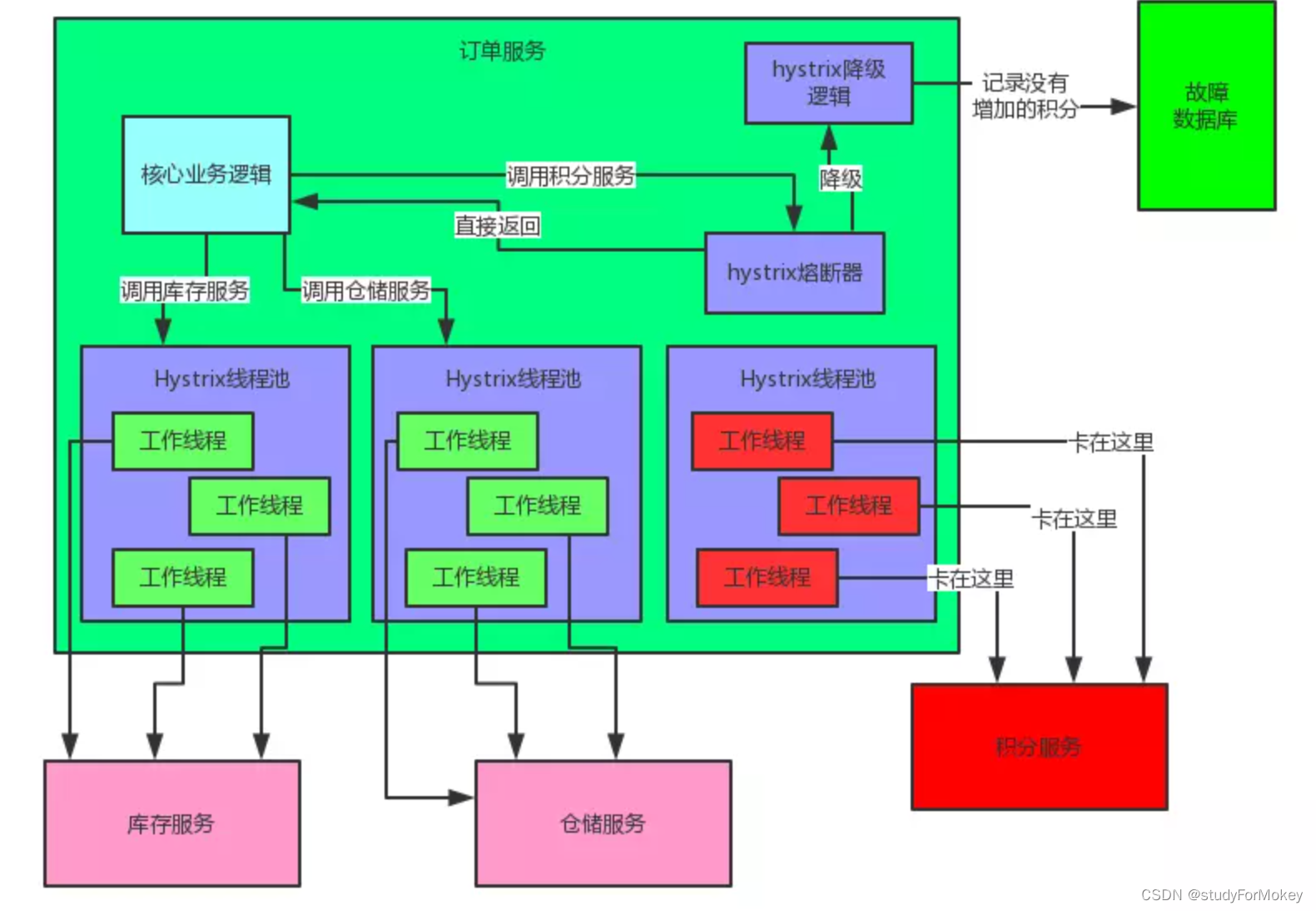
面经:微服务
文章目录 参考资料一. 微服务概述1. CAP理论2. BASE理论3. SpringBoot 与 SpringCloud对比 二. 服务注册:Zookeeper,Eureka,Nacos,Consul1. Nacos两种健康检查方式?2. nacos中负责负载均衡底层是如何实现的3. Nacos原理4. 临时实例和持久化(非临时)实例 …...

K8s 持久化存储有几种方式?一文了解本地盘/CSI 外接存储/K8s 原生存储的优缺点
当今云原生环境中,Kubernetes(K8s)已成为既定的容器编排工具。随着 K8s 的普及,存储也成为 K8s 用户关注的一个重要问题:为了满足不同的场景需求,K8s 可以支持基于不同架构的多种存储方案。这些方案间有什么…...

【MySQL】3、MySQL的索引、事务、存储引擎
create table class (id int not null,name char(10),score decimal(5,2)); insert into class values (1,zhangsan,80.5); update class set namewangwu,passwd123 where id2; select * from class where id2; drop 索引的概念 是一种帮助系统,能够更快速的查询信…...

【Hello Algorithm】链表相关算法题
本篇博客介绍: 介绍下链表相关的算法题 链表相关算法题 快慢指针回文结构链表将单向链表按某值划分为左边小,中间相等,右边大的形式复制带随机指针的链表 链表相关的算法题其实都算不上难 我们真正要考虑的是一些边界问题 事实上链表题就是在…...
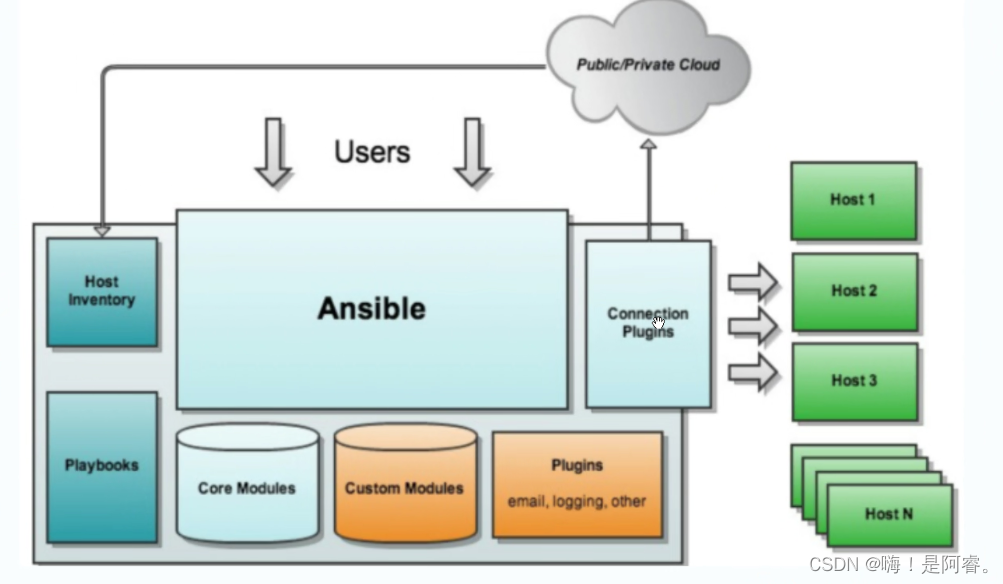
自动化管理管理工具----Ansible
目录 编辑 一、Ansible概念 1.1特点 二、工作机制(日常模块) 2.1 核心程序 三、Ansible 环境安装部署 四、ansible 命令行模块 4.1command 模块 4.2shell 模块 4.3cron 模块 4.4user 模块 4.5group 模块 4.6copy模块 4.7file模块 4.8ho…...

深入理解css3背景图边框
border-image知识点 重点理解 border-image-slice 设置的值将边框背景图分为9份,图像中间的舍弃,其他部分图像对应边框的相应区域放置,上右下左四角固定,border-image-repeat设置的是除四角外其他部分的显示方式。 截图来自菜鸟教…...

【rust/egui】(六)看看template的app.rs:TextEdit
说在前面 rust新手,egui没啥找到啥教程,这里自己记录下学习过程环境:windows11 22H2rust版本:rustc 1.71.1egui版本:0.22.0eframe版本:0.22.0上一篇:这里 TextEdit 文本编辑框 其定义为&#…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
