视觉SLAM14讲笔记-第4讲-李群与李代数
李代数的引出:
在优化问题中去解一个旋转矩阵,可能会有一些阻碍,因为它对加法导数不是很友好(旋转矩阵加上一个微小偏移量可能就不是一个旋转矩阵),因为旋转矩阵本身还有一些约束条件,那样再求导的过程中可能会破坏要优化的矩阵是旋转矩阵的本质条件,所以这里引入了一个乘法导数,即本章提到的左扰动或右扰动。
参考文献:https://www.cnblogs.com/dzyBK/p上/13961868.html
上一章我们知道旋转矩阵构成了特殊正交群 S O ( 3 ) SO(3) SO(3),变换矩阵构成了特殊欧式群 S E ( 3 ) SE(3) SE(3)。
群的引出:
这里我们简单叙述不做深入讨论。群是一种集合加上一种运算的代数结构。而李群是一种群,李群是指具有连续(光滑)性质的群,例如特殊正交群 S O ( 3 ) SO(3) SO(3)和特殊欧式群 S E ( 3 ) SE(3) SE(3),每个李群都有对应的李代数。
李代数的引出:
这里我们简单叙述不做深入讨论。李代数反应了李群的导数(局部)性质,在李群的正切空间上。而李群通过对数映射到李代数,李代数通过指数映射到李群。
经过推导,旋转矩阵对应的李代数就是旋转向量(3维)。变换矩阵对应的李代数是6维向量,平移在前,旋转在后。
使用李代数的一大动机是进行优化,而在优化过程中导数是非常必要的信息。
Baker-Campbell-Hausdorff公式的引出
l n ( e x p ( ϕ 1 ∧ ) e x p ( ϕ 2 ∧ ) ) ≈ { J l ( ϕ 2 ) − 1 ϕ 1 + ϕ 2 , if ϕ 1 is small J r ( ϕ 1 ) − 1 ϕ 2 + ϕ 1 , if ϕ 2 is small ln(exp(\phi_1^{\wedge})exp(\phi_2^{\wedge})) \approx \begin{cases} J_l(\phi_2)^{-1}\phi_1+\phi_2, & \text{if $\phi_1$ is small} \\[2ex] J_r(\phi_1)^{-1}\phi_2+\phi_1, & \text{if $\phi_2$ is small} \end{cases} ln(exp(ϕ1∧)exp(ϕ2∧))≈⎩ ⎨ ⎧Jl(ϕ2)−1ϕ1+ϕ2,Jr(ϕ1)−1ϕ2+ϕ1,if ϕ1 is smallif ϕ2 is small
BCH公式可以告诉我们当李代数发生了小量变化,旋转矩阵对应的变化,有利于计算出李代数导数,然而这个公式并不是万能的,用BCH线性近似来对李代数求导仍然有比较复杂的 J r J_r Jr,
所以下面我们使用扰动模型来对李代数求导,推导如下:
∂ ( R p ) ∂ φ = lim φ → 0 e x p ( φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ ≈ lim φ → 0 ( 1 + φ ∧ ) e x p ( ϕ ∧ ) p − e x p ( ϕ ∧ ) p φ = lim φ → 0 φ ∧ R p φ = lim φ → 0 − ( R p ) ∧ φ φ = − ( R p ) ∧ \dfrac{\partial(Rp)}{\partial\varphi} = \lim_{\varphi \to 0} \frac{exp(\varphi^{\wedge})exp(\phi^{\wedge})p-exp(\phi^{\wedge})p}{\varphi} \\ \approx \lim_{\varphi \to 0} \frac{(1+\varphi^{\wedge})exp(\phi^{\wedge})p-exp(\phi^{\wedge})p}{\varphi} \\ = \lim_{\varphi \to 0} \frac{\varphi^{\wedge}Rp}{\varphi} = \lim_{\varphi \to 0} \frac{-(Rp)^{\wedge}\varphi}{\varphi}=-(Rp)^{\wedge} ∂φ∂(Rp)=φ→0limφexp(φ∧)exp(ϕ∧)p−exp(ϕ∧)p≈φ→0limφ(1+φ∧)exp(ϕ∧)p−exp(ϕ∧)p=φ→0limφφ∧Rp=φ→0limφ−(Rp)∧φ=−(Rp)∧
第2行使用到 e x e^x ex的泰勒展开公式。
第3行使用到了公式 a ∧ b = − b ∧ a a^{\wedge}b=-b^{\wedge}a a∧b=−b∧a
同理, S E ( 3 ) SE(3) SE(3)上也有对应的扰动求导公式,这里不展开叙述了。
相似变换群与李代数(单目视觉)
由于单目的尺度不确定性,如果在单目SLAM中使用SE(3)表示位姿,那么由于尺度不确定性与尺度漂移,整个SLAM过程中的尺度会发生变化,这在 S E ( 3 ) SE(3) SE(3)中未能体现出来。因此,在单目情况下一般会显示地把尺度因子表达出来。用数学语言来说,对于位于空间的点p,在相机坐标系下要经过一个相似变换,而非欧式变换。
与SO(3)与SE(3)相似,相似变换亦对矩阵乘法构成群,称为相似变换群Sim(3)。
Sim(3)也有对应的李代数sim(3),他是一个7维向量 ζ \zeta ζ,它的前6维与se(3)相同,最后多了一项 σ \sigma σ。
写到最后,这一章偏理论,实际在写代码的时候我们会用ceses、g2o等库很方便直接计算出优化后的位姿。所以并不需要自己手动给出李代数的导数。有的话后续再分解。
相关文章:

视觉SLAM14讲笔记-第4讲-李群与李代数
李代数的引出: 在优化问题中去解一个旋转矩阵,可能会有一些阻碍,因为它对加法导数不是很友好(旋转矩阵加上一个微小偏移量可能就不是一个旋转矩阵),因为旋转矩阵本身还有一些约束条件,那样再求…...
浅析Redis(1)
一.Redis的含义 Redis可以用来作数据库,缓存,流引擎,消息队列。redis只有在分布式系统中才能充分的发挥作用,如果是单机程序,直接通过变量来存储数据是更优的选择。那我们知道进程之间是有隔离性的,那么re…...

【每日一题】2337. 移动片段得到字符串
【每日一题】2337. 移动片段得到字符串 2337. 移动片段得到字符串题目描述解题思路 2337. 移动片段得到字符串 题目描述 给你两个字符串 start 和 target ,长度均为 n 。每个字符串 仅 由字符 ‘L’、‘R’ 和 ‘_’ 组成,其中: 字符 ‘L’…...
MySQL 数据库常用命令大全(详细)
文章目录 1. MySQL命令2. MySQL基础命令3. MySQL命令简介4. MySQL常用命令4.1 MySQL准备篇4.1.1 启动和停止MySQL服务4.1.2 修改MySQL账户密码4.1.3 MySQL的登陆和退出4.1.4 查看MySQL版本 4.2 DDL篇(数据定义)4.2.1 查询数据库4.2.2 创建数据库4.2.3 使…...

中国移动加大布局长三角,打造算力产业新高地
8月27日,以“数实融合算启未来”为主题的2023长三角算力发展大会在苏州举办,大会启动了长三角算力调度枢纽,携手各界推动算力产业高质量发展。 会上,移动云作为第一批算力资源提供方,与苏州市公共算力服务平台签订算力…...

话费、加油卡、视频会员等充值接口如何对接?
现在很多商家企业等发现与用户保持粘性是越来越难了,大多数的用户活跃度都很差,到底该怎么做才能改善这种情况呢? 那么我们需要做的就是投其所好,在与用户保持粘性的app或者积分商城中投入大家感兴趣的物品或者虚拟产品ÿ…...

服务器重启MongoDB无法启动
文章目录 服务器重启MongoDB无法启动背景规划实施 总结 服务器重启MongoDB无法启动 背景 数据库服务器的CPU接近告警值了,需要添加CPU资源,于是乎就在恰当的时间对服务器进行关机,待添加完资源后开机,这样就完成了CPU资源的添加…...

深度刨析数据在内存中的存储
✨博客主页:小钱编程成长记 🎈博客专栏:进阶C语言 深度刨析数据在内存中的存储 1.数据类型介绍1.1 类型的基本归类 2.整形在内存中的存储2.1 原码、反码、补码2.2 大小端介绍 3.浮点型在内存中的存储3.1 一个例子3.2 浮点数的存储规则3.3指数…...
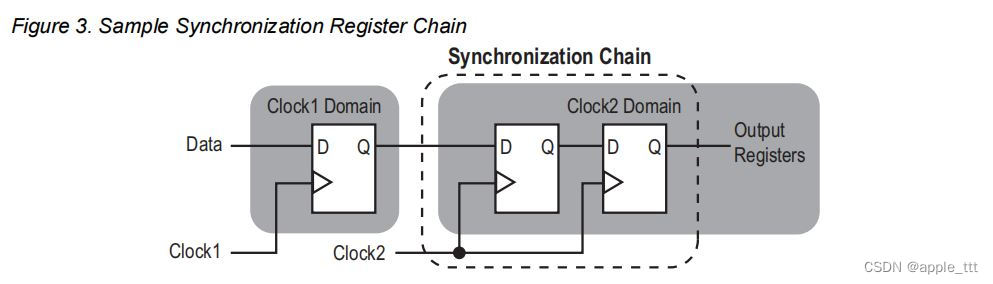
理解FPGA中的亚稳态
一、前言 大家应该经常能听说到亚稳态这个词,亚稳态主要是指触发器的输出在一段时间内不能达到一个确定的状态,过了这段时间触发器的输出随机选择输出0/1,这是我们在设计时需要避免的。本文主要讲述了FPGA中的亚稳态问题,可以帮助…...

Leetcode86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。 你应当 保留 两个分区中每个节点的初始相对位置。 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台…...

如何处理 Flink 作业中的数据倾斜问题?
分析&回答 什么是数据倾斜? 由于数据分布不均匀,造成数据大量的集中到一点,造成数据热点。 举例:一个 Flink 作业包含 200 个 Task 节点,其中有 199 个节点可以在很短的时间内完成计算。但是有一个节点执行时间…...
cobbler自动化安装CentOS、windows和ubuntu
环境介绍 同时玩cobbler3.3和cobbler2.8.5 cobbler3.3 系统CentOS8.3 VMware虚拟机 桥接到物理网络 IP: 192.168.1.33 cobbler2.8.5 系统CentOS7.9 VMWare虚拟机 桥接到物理网络 IP:192.168.1.33 安装cobbler3.3 yum源修改 cat /etc/yum.repo.d/Cento…...

springcloud3 GateWay章节-Nacos+gateway动态路由负载均衡4
一 工程结构 1.1 工程 1.2 搭建gatewayapi工程 1.pom文件 <dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>4.13</version><scope>test</scope></dependency><!--gateway--&g…...

RESTful API 面试必问
RESTful API是一种基于 HTTP 协议的 API 设计风格,它提供了一组规范和约束,使得客户端(如 Web 应用程序、移动应用等)和服务端之间的通信更加清晰、简洁和易于理解。 RESTful API 的设计原则 使用 HTTP 协议:RESTful …...

软件机器人助力行政审批局优化网约车业务流程,推动审批业务数字化转型
随着社会的进步和发展,行政审批业务逐渐趋向于智能化和自动化。近日,某市行政审批局在市场准入窗口引入博为小帮软件机器人大幅度提升了网约车办理业务的效率,创新了原有的业务模式。 软件机器人以其自动化、智能化的特性,优化了网…...
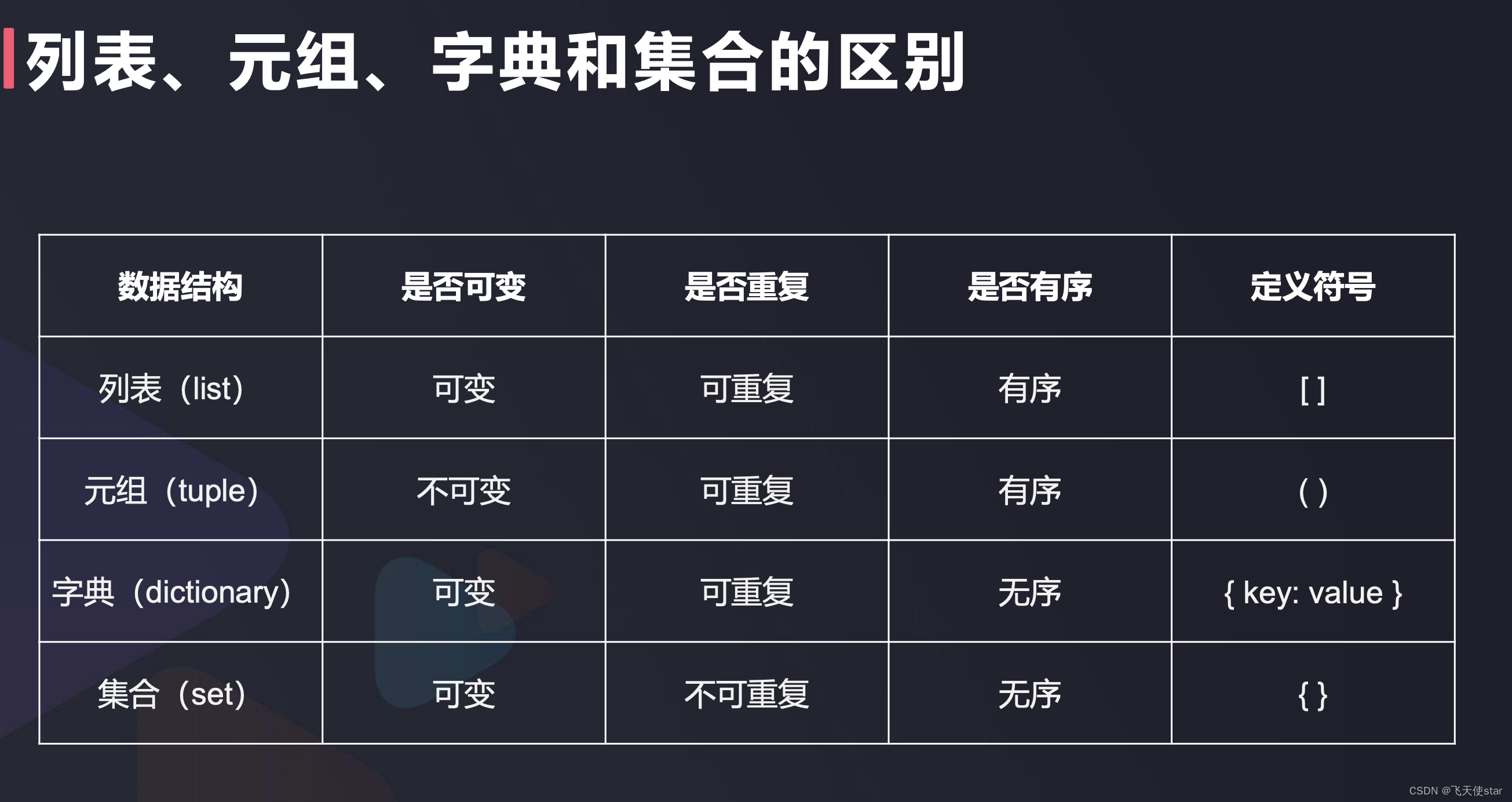
飞天使-python的字符串转义字符元组字典等
文章目录 基础语法数据类型python的字符串运算符输入和输出 数据结构列表与元组字典与集合 参考文档 基础语法 数据类型 数值型 ,整数 浮点型 布尔型, 真假, 假范围 字符型 类型转换python的字符串 了解转义字符一些基本的运算 \ 比如一行…...

stm32 uart dma方式接收不定长度字符
一般处理: stm32 uart使用dma接收时,会有自己的数据流中断,数据流中断会调用HAL_UART_RxCpltCallback。但是数据流中断只会在HAL_UART_Receive_DMA函数指定的buffer满时才会触发。 接收不定长度字符,需要和uart的UART_IT_IDLE结…...

SciencePub学术 | Elsevier出版社SCIEEI征稿中
SciencePub学术刊源推荐:Elsevier出版社SCIE&EI征稿中!信息如下,录满为止: 一、期刊概况: 计算机科学类SCI-01 【期刊简介】6.5-7.0,JCR1区,中科院2区; 【检索情况】正刊,SC…...
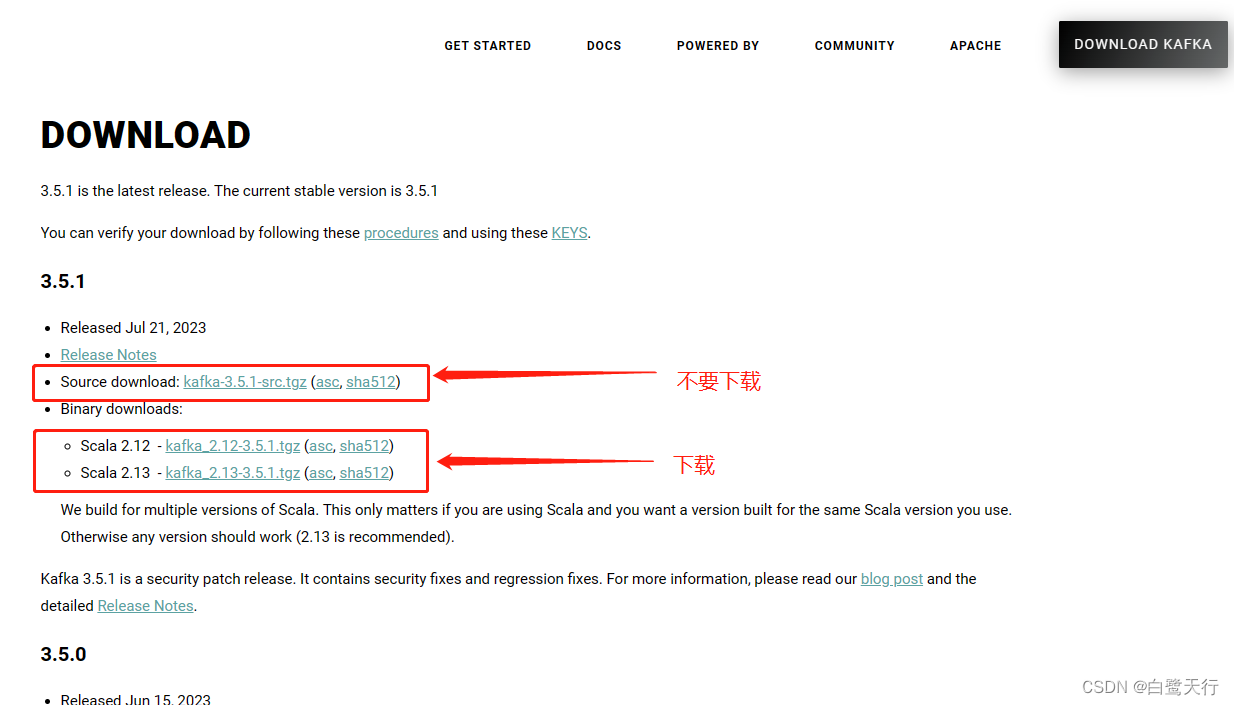
PHP小白搭建Kafka环境以及初步使用rdkafka
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、安装java(Kafka必须安装java,因为kafka依赖java核心)二、安装以及配置Kafka、zookeeper1.下载Kafka(无需下载…...

【Java Web】敏感词过滤
一、前缀树 假设有敏感词:b,abc,abd,bcd,abcd,efg,hii 那么前缀树可以构造为: 二、敏感词过滤器 package com.nowcoder.community.util;import org.apache.commons.lang3.CharUt…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
