数据结构:排序解析
文章目录
- 前言
- 一、常见排序算法的实现
- 1.插入排序
- 1.直接插入排序
- 2.希尔排序
- 2.交换排序
- 1.冒泡排序
- 2.快速排序
- 1.hoare版
- 2.挖坑版
- 3.前后指针版
- 4.改进版
- 5.非递归版
- 3.选择排序
- 1.直接选择排序
- 2.堆排序
- 4.归并排序
- 1.归并排序递归实现
- 2.归并排序非递归实现
- 5.计数排序
- 二、排序算法复杂度及稳定性
- 排序测试
前言
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。排序在我们生活中非常常见,比如买东西看的销量,价格的对比等。排序也分为内部排序和外部排序。内部排序是数据元素全部放在内存中的排序,外部排序则是数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。下面让我们正式认识排序吧。
一、常见排序算法的实现
1.插入排序
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
1.直接插入排序
void InsertSort(int* nums, int numsSize)
{int i = 0;//i变量控制的是整个比较元素的数量for (i = 0; i < numsSize; i++){int num = nums[i];//从后面一次和前面的元素进行比较,前面的元素大于后面的数据,则前面的元素向后移动int j = i - 1;while (j > -1){if (nums[j] > num){//要交换的元素小于前一个元素nums[j + 1] = nums[j];j--;}else{break;}}//把该元素填到正确的位置nums[j + 1] = num;}
}
测试用例:
void sortArray(int* nums, int numsSize)
{InsertSort(nums, numsSize);//插入排序
}
void print(int* nums, int numsSize)
{int i = 0;for (i = 0; i < numsSize; i++){printf("%d ", nums[i]);}
}
int main()
{int nums[] = { 3,9,0,-2,1 };int numsSize = sizeof(nums) / sizeof(nums[0]);//计算数组大小sortArray(nums, numsSize);//调用排序算法print(nums, numsSize);//打印排序结果return 0;
}

直接插入排序的优点:元素集合越接近有序,直接插入排序算法的时间效率越高。
时间复杂度:O(N ^2)
空间复杂度O(1)
直接插入排序是一种稳定的排序算法。
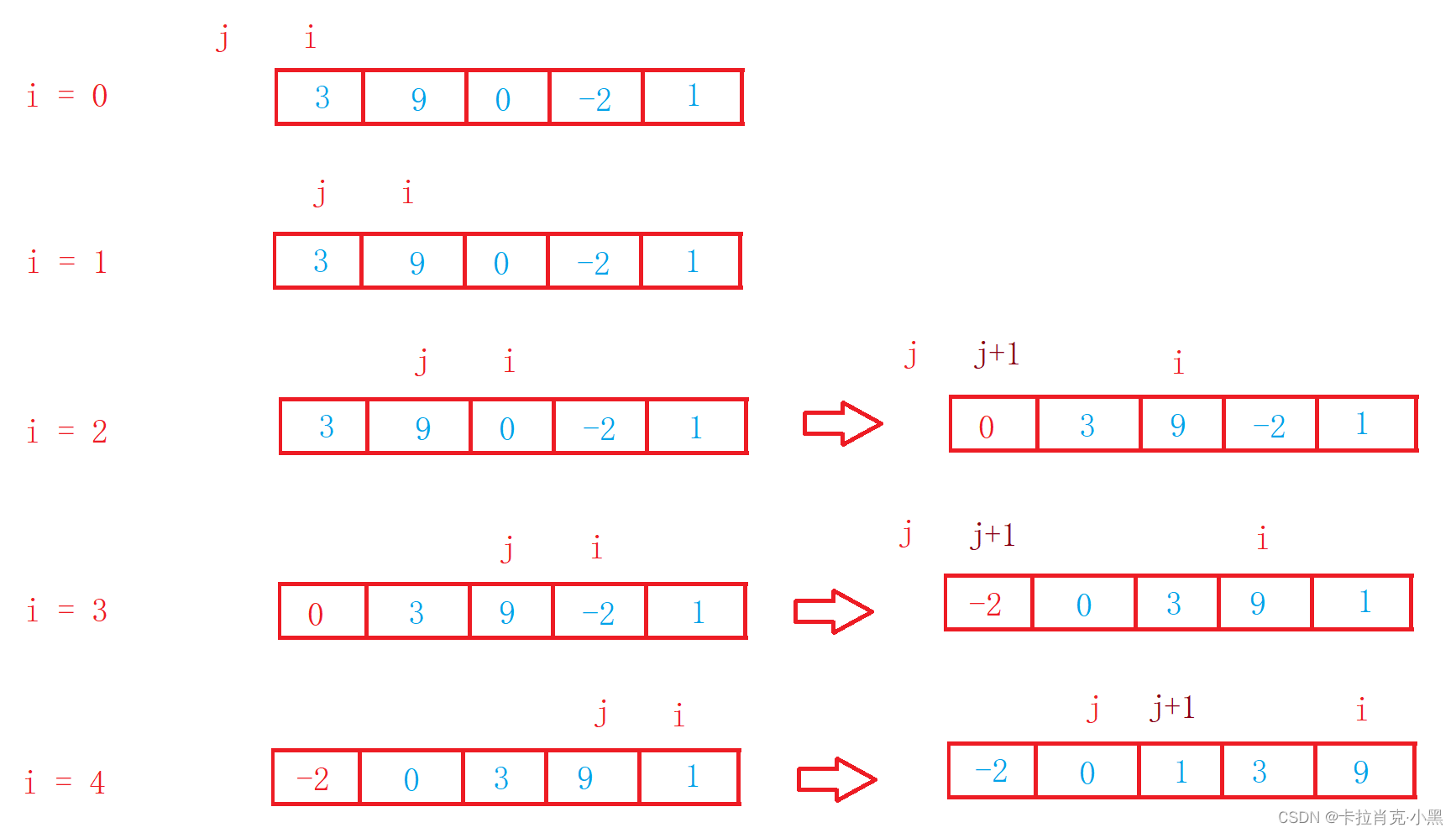
2.希尔排序
将待排序的序列分成若干个子序列,对每个子序列进行插入排序,使得整个序列基本有序,然后再对整个序列进行插入排序。是插入排序的改进
void ShellSort(int* nums, int numsSize)
{int group = numsSize;while (group > 1){//进行分组//加1为了保证最后一次分组为1,组后一次必须要进行正常的插入排序group = group / 3 + 1;int i = 0;//每次对分的组进行排序//和插入排序思路相同for (i = 0; i < numsSize; i++){int num = nums[i];int j = i - group;while (j >= 0){if (nums[j] > num){nums[j + group] = nums[j];j -= group;}else{break;}}nums[j + group] = num;}}
}
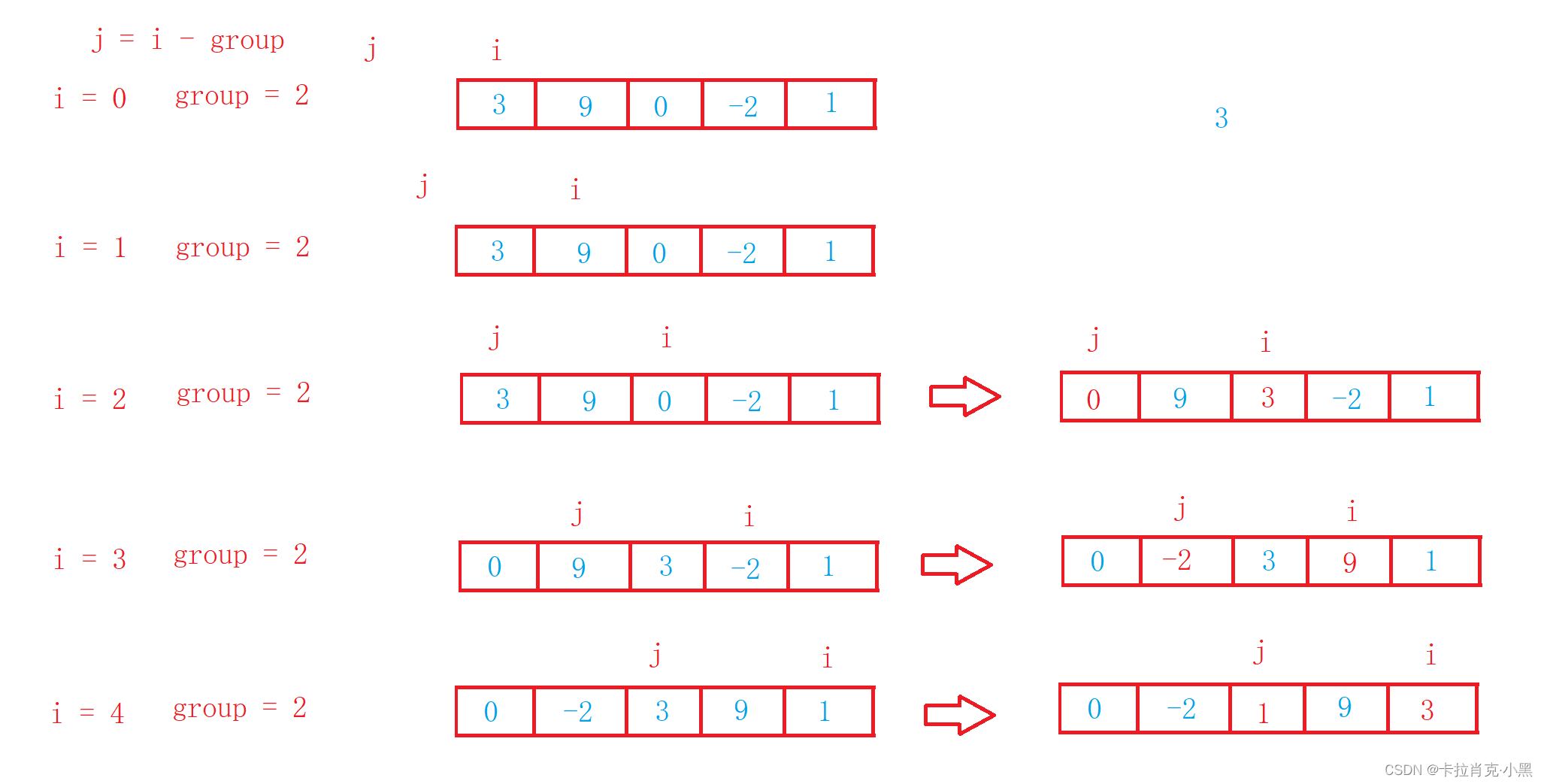
group为1时为插入排序,必须要保证最后一次group为1,这样排序才能正确。希尔排序法也称缩小增量法
希尔排序是对直接插入排序的优化。
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
当group > 1时都是预排序,目的是让数组更接近于有序,让大的数能更快到达后面,小的数可以更快到达前面。当group = 1时,数组已经接近有序的了,这时间使用插入可以让插入排序时间复杂度接近O(N)。从而达到优化效果。希尔排序的时间复杂度大约为O(N^1.3)。
测试用例:
void sortArray(int* nums, int numsSize)
{//InsertSort(nums, numsSize);//插入排序ShellSort(nums, numsSize);//希尔排序
}
int main()
{int nums[] = { 3,9,0,-2,1 };int numsSize = sizeof(nums) / sizeof(nums[0]);//计算数组大小sortArray(nums, numsSize);//调用排序算法print(nums, numsSize);//打印排序结果return 0;
}

2.交换排序
1.冒泡排序
void BubbleSort(int* nums, int numsSize)
{int i = 0;//控制循环次数for (i = 0; i < numsSize; i++){int j = 0;//用记录该数组是否有序可以提前退出循环int flag = 0;//用来控制比较次数for (j = 0; j < numsSize - i - 1; j++){if (nums[j + 1] < nums[j]){swap(&nums[j], &nums[j + 1]);flag = 1;}}//当该此循环不在进行交换则证明数组已经有序,可以提前退出循环if (flag == 0){break;}}
}
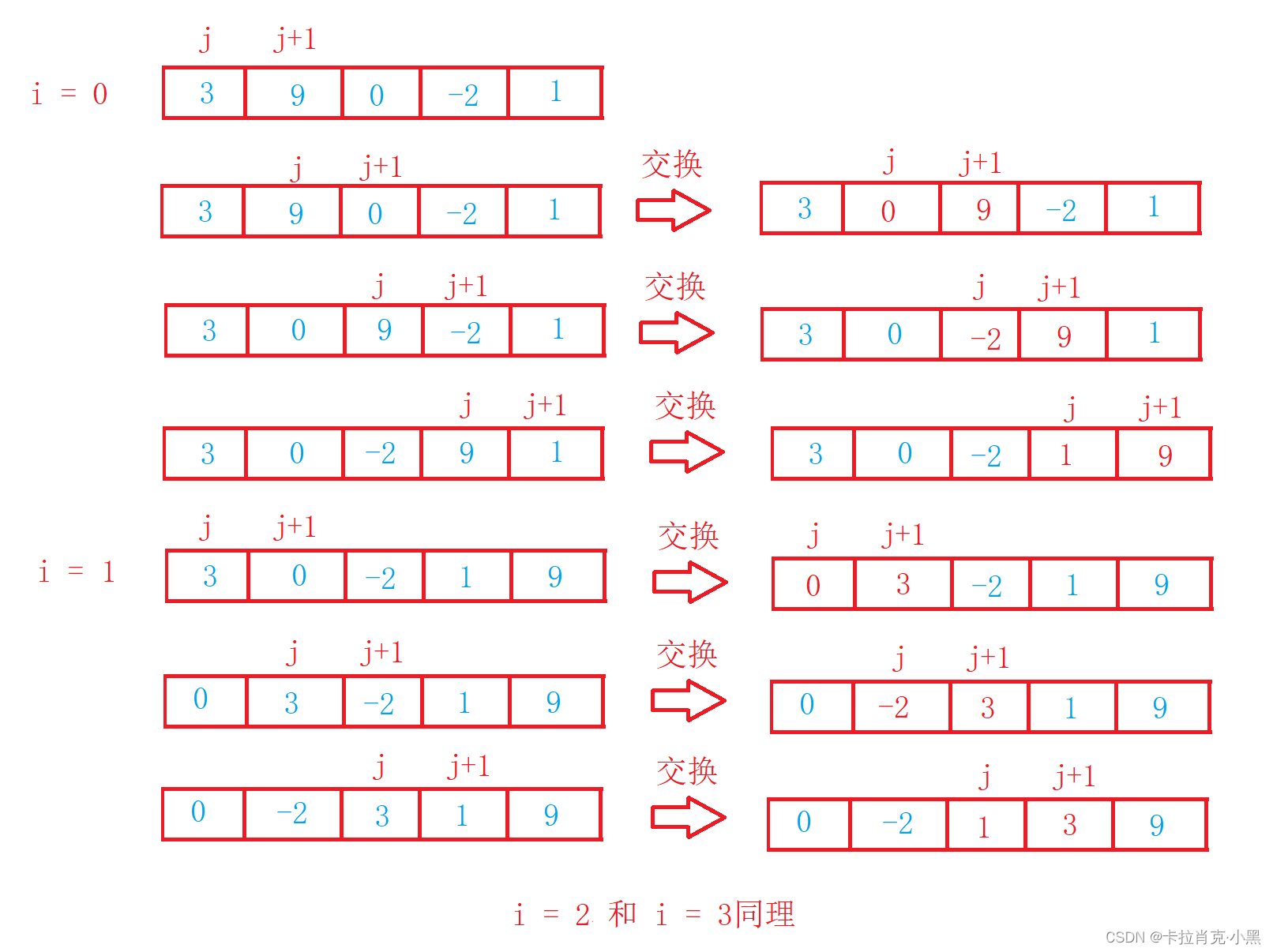
冒泡排序非常容易理解,它的时间复杂度为O(N^2) ,空间复杂度:O(1)且很稳定。
2.快速排序
任取待排序元素序列中的某元素作为标准值,按照该排序码将待排序集合分成两段,左边中所有元素均小于该值,右边中所有元素均大于该值,然后左右两边重复该过程,直到所有元素都排列在相应位置上为止。
1.hoare版
void PartSort1(int* nums, int left, int right)
{//当区间不存在或者区间只有一个数时结束递归if (left >= right){return ;}int key = left;int begin = left;int end = right;while (begin < end){//右边先走,目的是结束是相遇位置一定比key值小//开始找比选定值小的元素while ((begin < end) && (nums[key] <= nums[end])){end--;}//开始找比选定值大的元素while ((begin < end) && (nums[begin] <= nums[key])){begin++;}//把两个数进行交换swap(&nums[begin], &nums[end]);}//把关键值和相遇点的值进行交换,由于右边先走,相遇值一定小于关键值swap(&nums[key], &nums[begin]);key = begin;//开始递归左边区间PartSort1(nums, left, key - 1);//开始递归右边区间PartSort1(nums, key + 1, right);
}
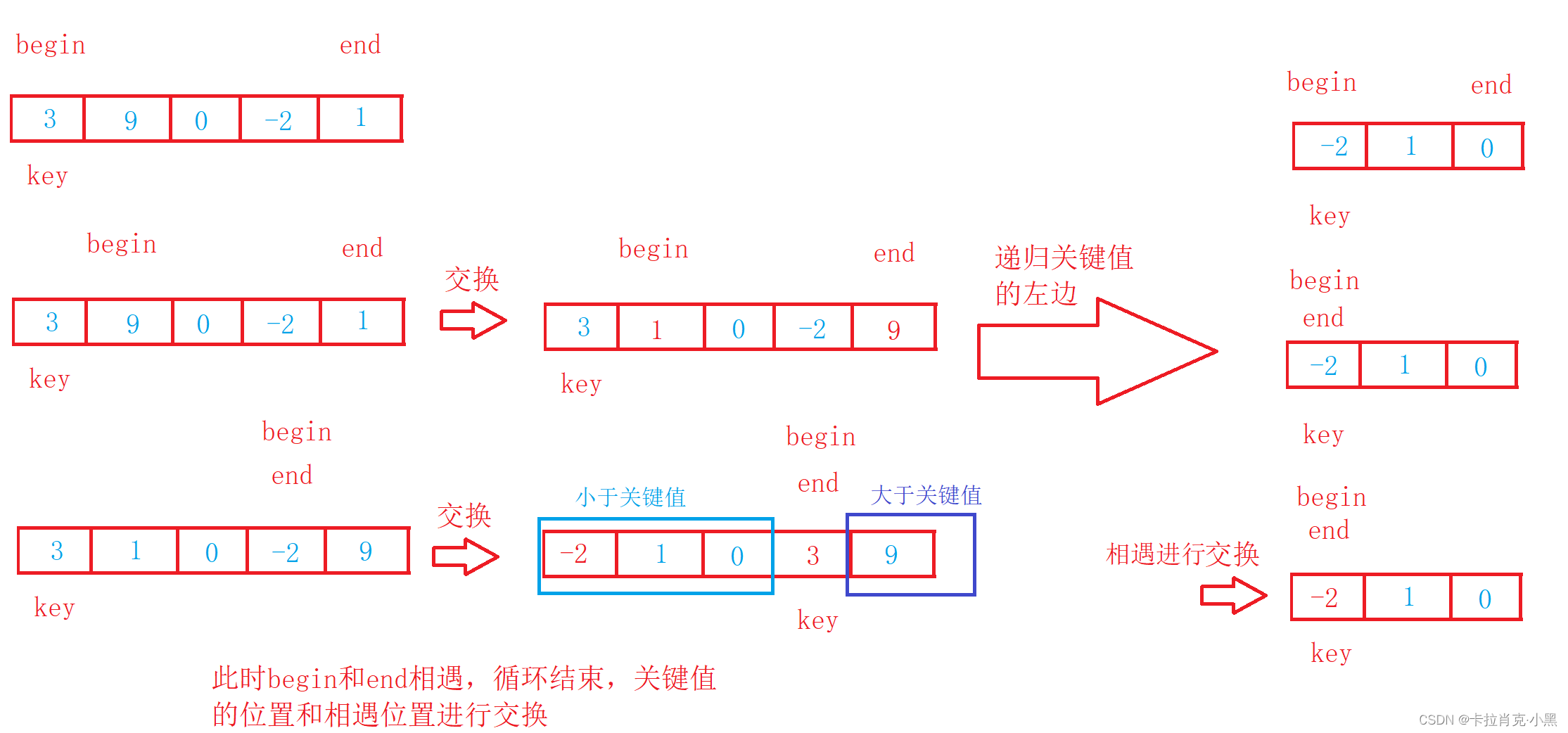
分别递归左右区间,直到递归为不可在分割的区间,是分治算法,每次递归都会有一个数回到正确的位置。
2.挖坑版
void PartSort2(int* nums, int left, int right){if (left >= right){return;} int hole = left;//坑的位置 int key = nums[left];//记录初始坑位置的值int begin = left;int end = right;while (begin < end){while ((begin < end) && (key <= nums[end])){end--;} nums[hole] = nums[end];//把小于初始坑位置的填到坑中hole = end;//更新坑的位置while ((begin < end) && (nums[begin] <= key)){begin++;}nums[hole] = nums[begin];//把大于初始坑位置的填到坑中hole = begin;//更新坑的位置}//坑的位置放置初始坑位置的值nums[begin] = key;//开始递归左边区间PartSort2(nums, left, hole - 1);//开始递归右边区间PartSort2(nums, hole + 1, right);}
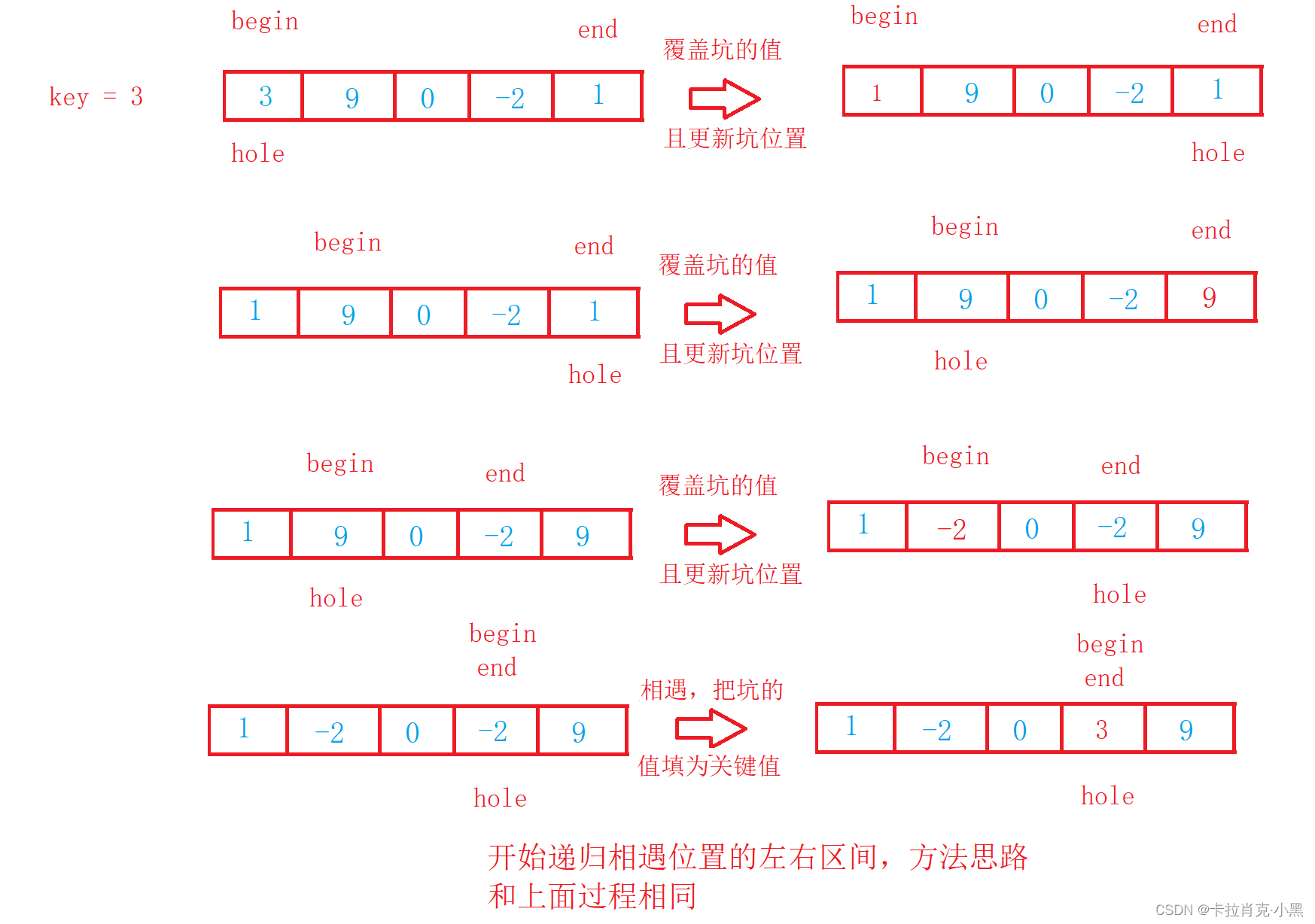
注意要先将第一个数据存起来,形成第一个坑位才可以进行覆盖。
3.前后指针版
void PartSort3(int* nums, int left, int right){if (left >= right){return;}//记录关键值int key = nums[left];//快指针为关键值的下一个位置int fast = left + 1;//慢指针为关键值的位置int slow = left;while (fast <= right){//当快指针的值小于关键值时if (nums[fast] < key){//当慢指针的下一个不为快指针时则不进行交换if (++slow != fast){swap(&nums[fast], &nums[slow]); }}//对快指针进行移动fast++;//简写形式//if (nums[fast] < key && ++slow != fast)//{// swap(&nums[slow], &nums[fast]);//}//++fast;}//关键值的位置和慢指针进行交换swap(&nums[left], &nums[slow]);//开始递归左边区间PartSort3(nums, left, slow - 1);//开始递归右边区间PartSort3(nums, slow + 1, right);}
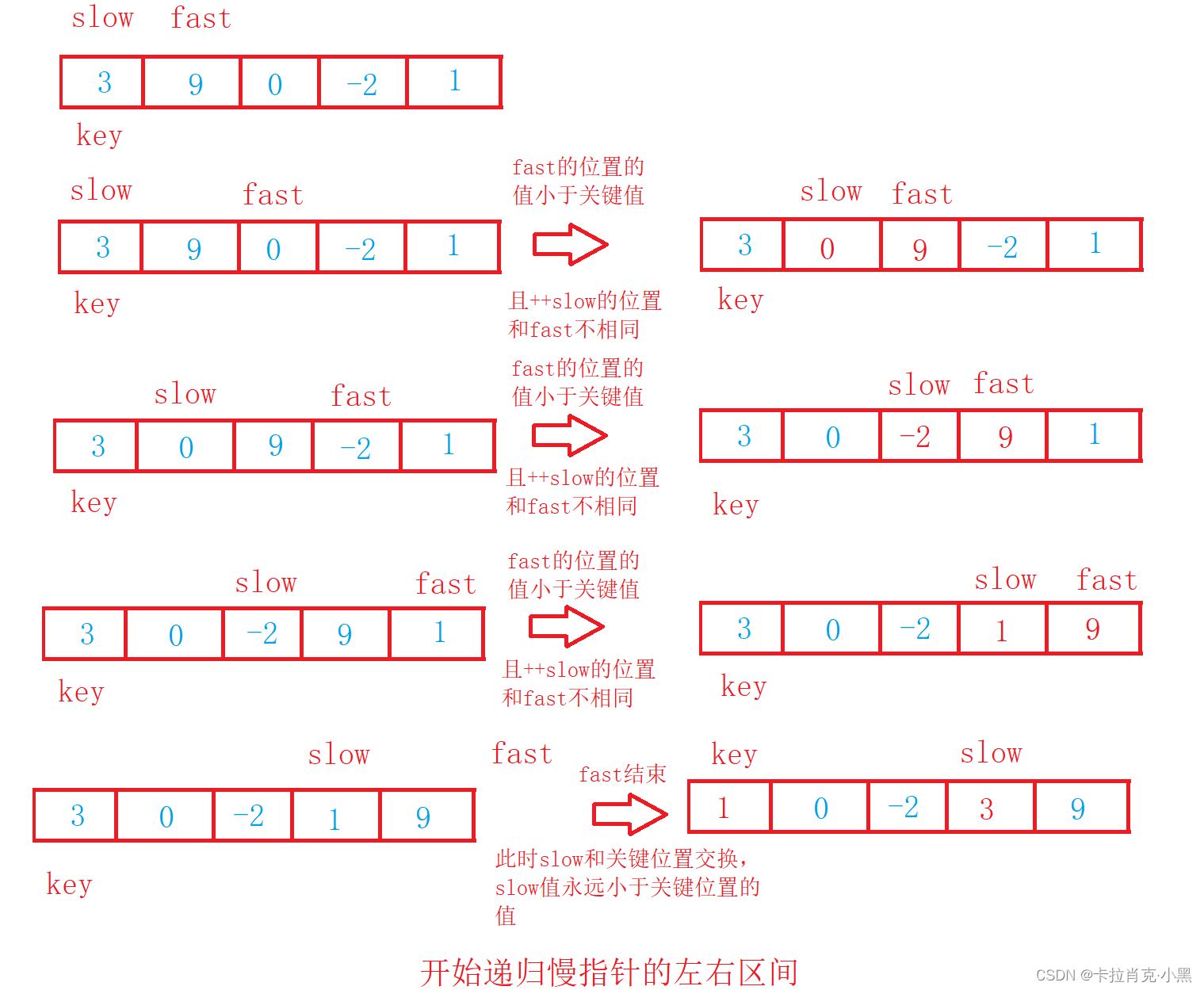
4.改进版
当要排序的区间为有序时,我们排序就是最坏的情况,这时间就需要我们进行优化一下。
我们要加三数取中操作。
//三数取中
void middle(int* nums, int left, int right)
{//找到中间的数,交换到数组开头,因为我们关键值选则的为数组的左边值int middle = (left + right) / 2;if (nums[left] < nums[middle]){if (nums[middle] < nums[right]){swap(&nums[left], &nums[middle]);}else{swap(&nums[left], &nums[right]);}}else{if (nums[right] < nums[left]){swap(&nums[left], &nums[right]);}}
}
void QuickSort(int* nums, int left, int right)
{if (left >= right){return;}middle(nums, left, right);//把中间值换到排序的开始位置int key = left;int begin = left;int end = right;while (begin < end){//右边先走,目的是结束是相遇位置一定比key值小while ((begin < end) && (nums[key] <= nums[end])){end--;}while ((begin < end) && (nums[begin] <= nums[key])){begin++;}swap(&nums[begin], &nums[end]);}swap(&nums[key], &nums[begin]);key = begin;QuickSort(nums, left, key - 1);QuickSort(nums, key + 1, right);
}
我们实现的版本1的改进,版本2和3改进同理,只是增加一个调用函数。
5.非递归版
当我们拍的数据递归调用太深的情况就会造成栈破坏,所以非递归版本的快排也是重中之重。让我们实现一下吧。非递归中我们用到之前学的栈来辅助我们完成。
void QuickSortNonR(int* nums, int left, int right)
{Stack st;//创建栈StackInit(&st);//初始话栈StackPush(&st, right);//把要排序的右边界入栈,这时会先左边界先出栈StackPush(&st, left);//把要排序的左边界入栈while (!StackEmpty(&st))//如果栈不为空,则一直进行循环{int left = StackTop(&st);//获得要排序的左边界StackPop(&st);//把左边界出栈int right = StackTop(&st);//获得要排序的右边界StackPop(&st);//把右边界出栈if (left >= right)//如果边界不合法则跳过本次循环{continue;}//快速排序版本1int key = left;int begin = left;int end = right;while (begin < end){//右边先走,目的是结束是相遇位置一定比key值小while ((begin < end) && (nums[key] <= nums[end])){end--;}while ((begin < end) && (nums[begin] <= nums[key])){begin++;}swap(&nums[begin], &nums[end]);}swap(&nums[key], &nums[begin]);key = begin;StackPush(&st, key-1);//把左边界的结束位置入栈StackPush(&st, left);//把左边界的起始位置入栈StackPush(&st, right);//把右边界的结束位置入栈StackPush(&st, key+1);//把右边界的起始位置入栈}StackDestroy(&st);//销毁栈
}
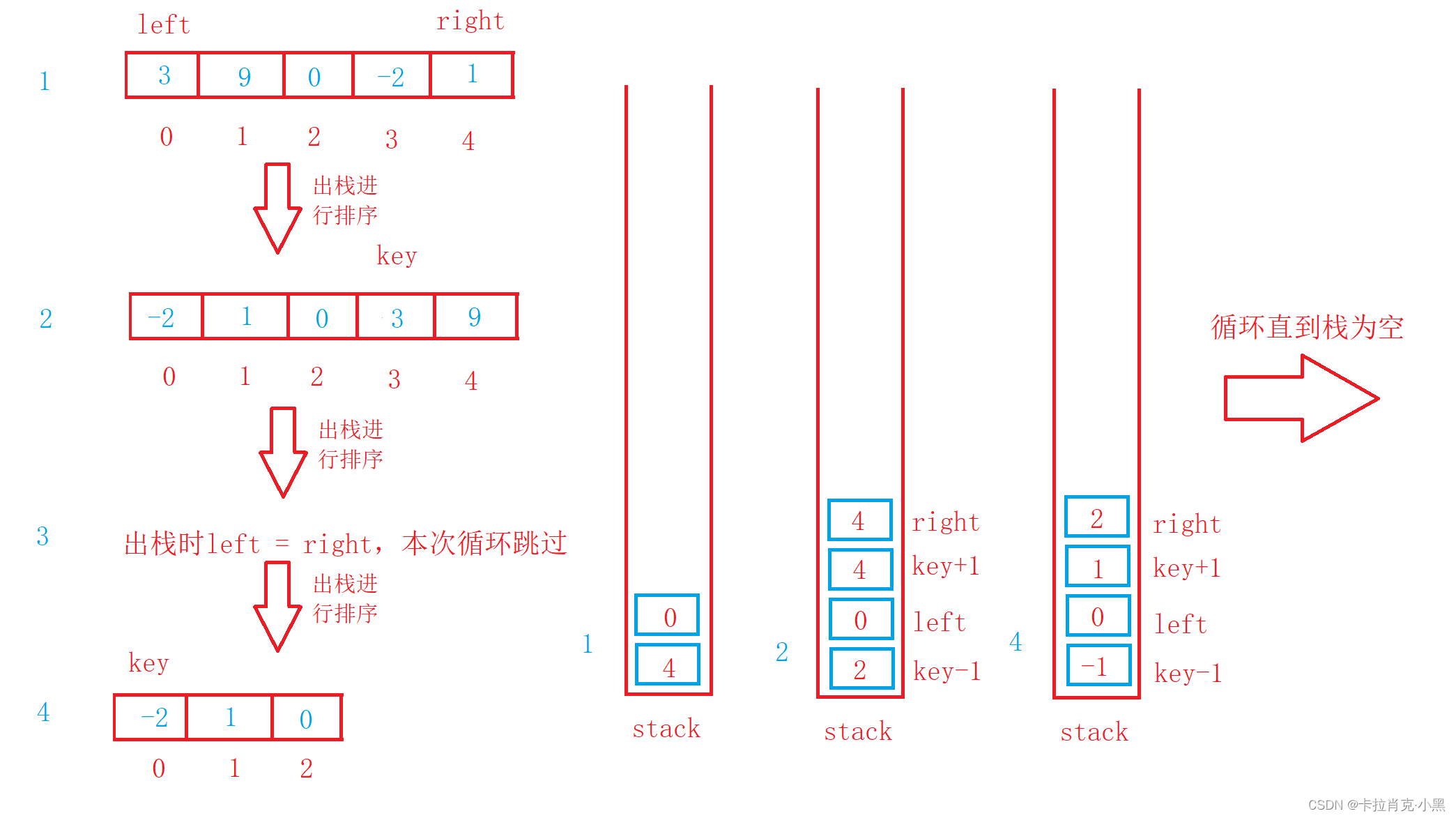
快排在一般情况下效率非常高,且可以搭配其他排序进行小区间优化。它的时间复杂度为O(N*logN),空间复杂度为O(logN),但不稳定
3.选择排序
每一次从待排序的数据元素中选出最小(或最大)的一个值,存放在数据的起始位置,直到全部待排序的数据元素排完。
1.直接选择排序
void SelectSort(int* nums, int numsSize)
{int i = 0;for (i = 0; i < numsSize; i++){int min = i;//记录最小数的下标int j = 0;for (j = i; j < numsSize; j++)//开始寻找最小数{if (nums[j] < nums[min]){min = j;//记录下标}}if (min != i){swap(&nums[min], &nums[i]);//如果最小数和开始位置不相同则进行交换}}
}
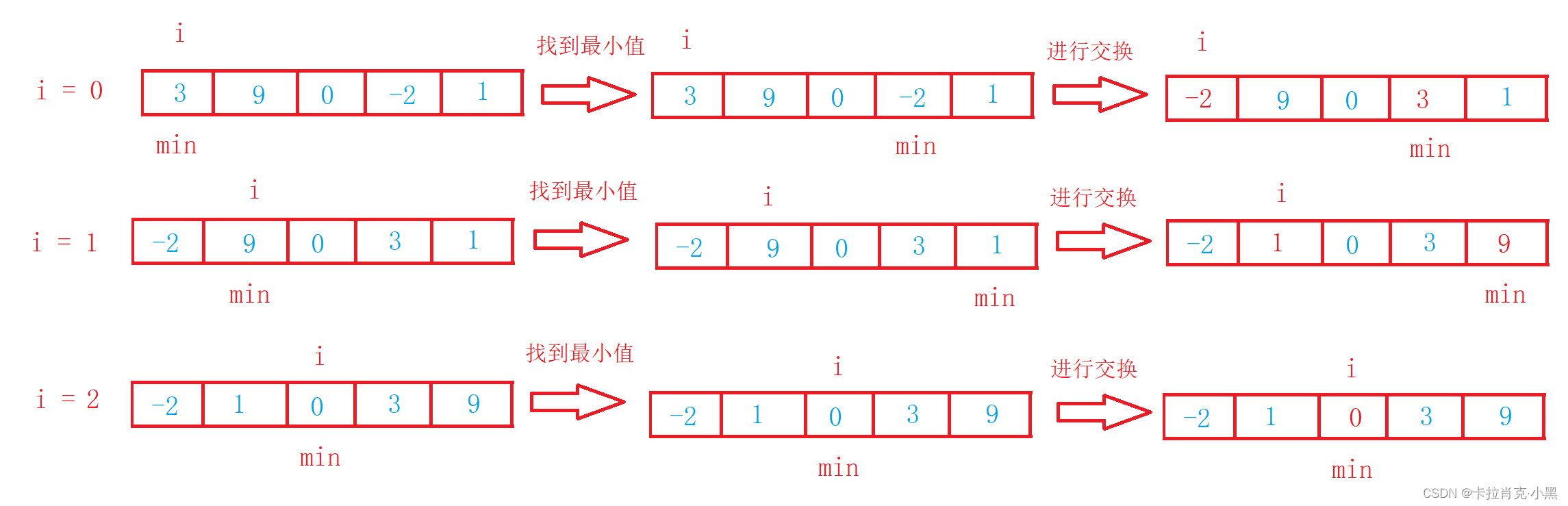
直接选择排序非常好理解,但是效率太低。实际中很少使用
2.堆排序
堆的思想和树一样。堆排序是指利用堆积树(堆)这种数据结构所设计的一种排序算法,我们升序要建大堆,降序要建小堆
void AdjustDwon(int* nums, int n, int root)
{int left = root * 2 + 1;while (left < n){if (((left + 1) < n) && (nums[left] < nums[left + 1]))//当右子树存在并且右子树的值大于左子树{left = left + 1;//更新节点的下标}if (nums[root] < nums[left]){swap(&nums[root], &nums[left]);//如果根节点小于孩子节点,就进行交换root = left;//更新根节点left = root * 2 + 1;//更新孩子节点}else//已符合大堆结构,跳出循环{break;}}
}
//建大堆
void HeapSort(int* nums, int numsSize)
{int i = 0;//从第一个非叶子节点开始进行建堆,当左右都为大堆时才会排根节点for (i = (numsSize - 1 - 1) / 2; i >= 0; --i){AdjustDwon(nums, numsSize, i);}while (numsSize--){swap(&nums[0], &nums[numsSize]);//如果根节点小于孩子节点,就进行交换//调整堆结构AdjustDwon(nums, numsSize, 0);}
}
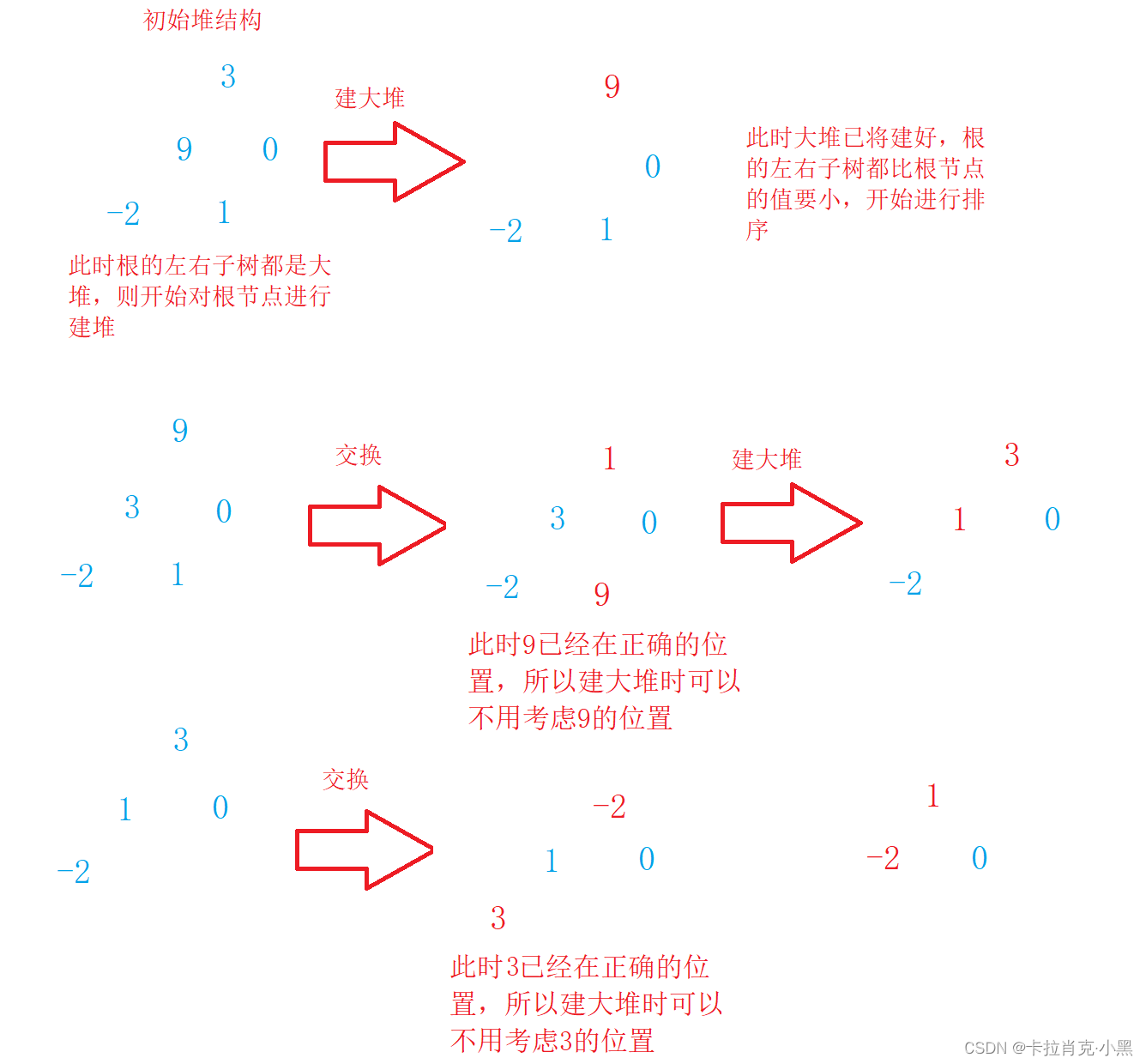
堆排序使用堆来选数,效率比直接排序高很多。它的时间复杂度为O(N*logN),且空间复杂度为O(1),但是不稳定。
4.归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法。先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表。归并需要一个临时的空间来存放子序列,用来拷贝到源序列中
1.归并排序递归实现
void MergeSort(int* nums, int left, int right,int *tmp)
{if (left >= right){return;}//把区间拆分为两段int middle = (left + right) >> 1;//拆分MergeSort(nums, left, middle, tmp);MergeSort(nums, middle+1, right, tmp);//归并int begin1 = left;int begin2 = middle + 1;int end1 = middle;int end2 = right;int i = 0;//和链表的链接差不多//直到有一个区间结束结束循环while ((begin1 <= end1) && (begin2 <= end2)){//那个值小那个值进入开辟的数组if (nums[begin1] <= nums[begin2]){tmp[i++] = nums[begin1++];}else{tmp[i++] = nums[begin2++];}}//找到未完全结束的数组,并且把数组中的元素尾加到开辟的数组中while (begin1 <= end1){tmp[i++] = nums[begin1++];}while (begin2 <= end2){tmp[i++] = nums[begin2++];}//把开辟的数组中的内容拷贝到源数组中//拷贝时要注意拷贝时的位置memcpy(nums + left, tmp, (right - left + 1) * sizeof(int));
}
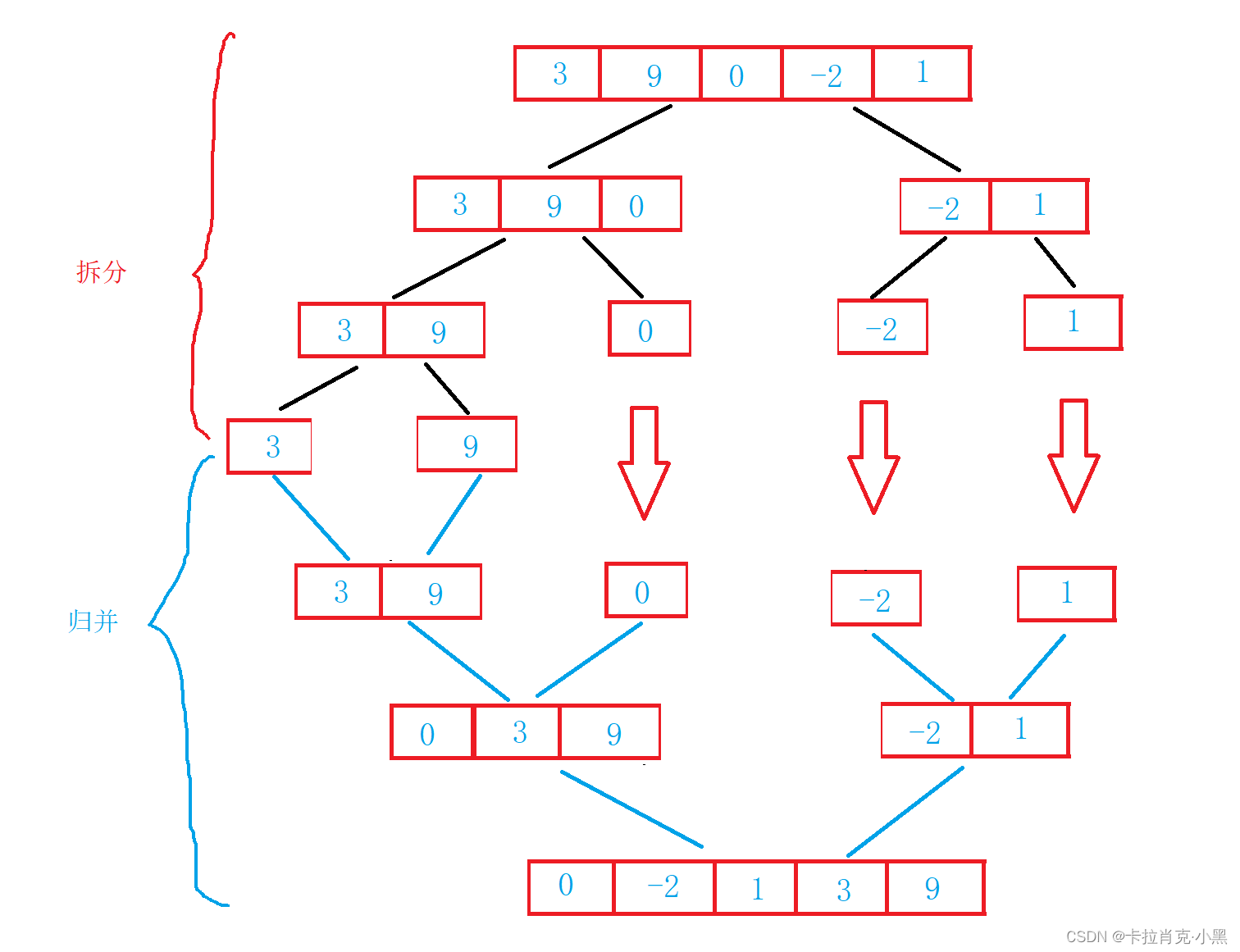
2.归并排序非递归实现
void MergeSortNonR(int* nums, int numsSize, int* tmp)
{//归并所用的数int gap = 1;int i = 0;while(gap < numsSize)//当归并使用的数小于数组大小时进行循环{for (i = 0; i < numsSize;)//用i来控制归并的位置{int begin1 = i;int begin2 = i + gap;int end1 = i + gap - 1;int end2 = i + 2 * gap - 1;//当end1越界时进行修正,此时begin2和end2都会越界时进行修正if (end1 > numsSize - 1){end1 = numsSize - 1;begin2 = numsSize + 1;end2 = numsSize;}//当begin2越界时进行修正,此时end2也会越界else if (begin2 > numsSize - 1){begin2 = numsSize + 1;end2 = numsSize;}//当end2越界时进行修正else if(end2 > numsSize - 1){end2 = numsSize - 1;}//开始进行归并while ((begin1 <= end1) && (begin2 <= end2)){if (nums[begin1] <= nums[begin2]){tmp[i++] = nums[begin1++];}else{tmp[i++] = nums[begin2++];}}//找到未结束的数组插入到临时数组中while (begin1 <= end1){tmp[i++] = nums[begin1++];}while (begin2 <= end2){tmp[i++] = nums[begin2++];}}//把临时数组的内容拷贝到源数组中memcpy(nums, tmp, numsSize * sizeof(int));//把归并的范围扩大gap *= 2;}
}
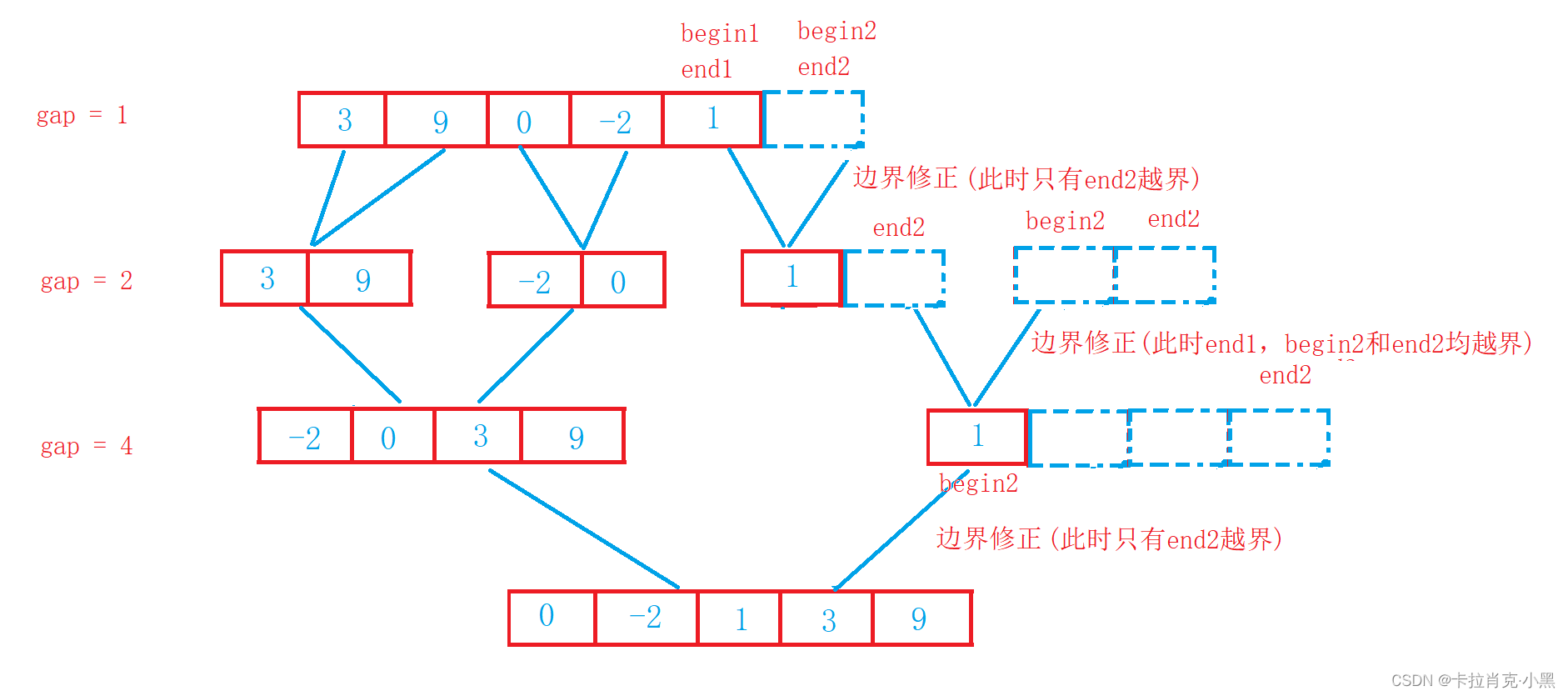
归并排序的非递归要注意边界的修正,不然会产生越界的情况。
归并的缺点在于需要O(N)的空间,但归并排序的思考更多的是解决在磁盘中的外排问题。可以当内排序,也可以当外排序使用,且时间复杂度为O(N*logN),是一种稳定的排序。
5.计数排序
void CountSort(int* nums, int numsSize)
{int i = 0;int min = nums[i];int max = nums[i];//找到原数组中的最大值和最小值for (i = 0; i < numsSize; i++){if (min > nums[i]){min = nums[i];}if (max < nums[i]){max = nums[i];}}//计算出排序中最大和最小值的差,加上1为要开辟临时数组的大小int num = max - min + 1;//创建相应的大小的空间int* tmp = (int*)malloc(sizeof(int) * num);//对创建的空间进行初始话,把里面的元素全部置0memset(tmp, 0, sizeof(int) * num);//遍历原数组,把该元素值的下标映射到临时数组中for (i = 0; i < numsSize; i++){tmp[nums[i] - min]++;}int j = 0;//遍历临时数组,把该元素不为0的恢复原值拷贝到原数组中for (i = 0; i < num; i++){while (tmp[i]--){nums[j++] = i + min;}}free(tmp);
}
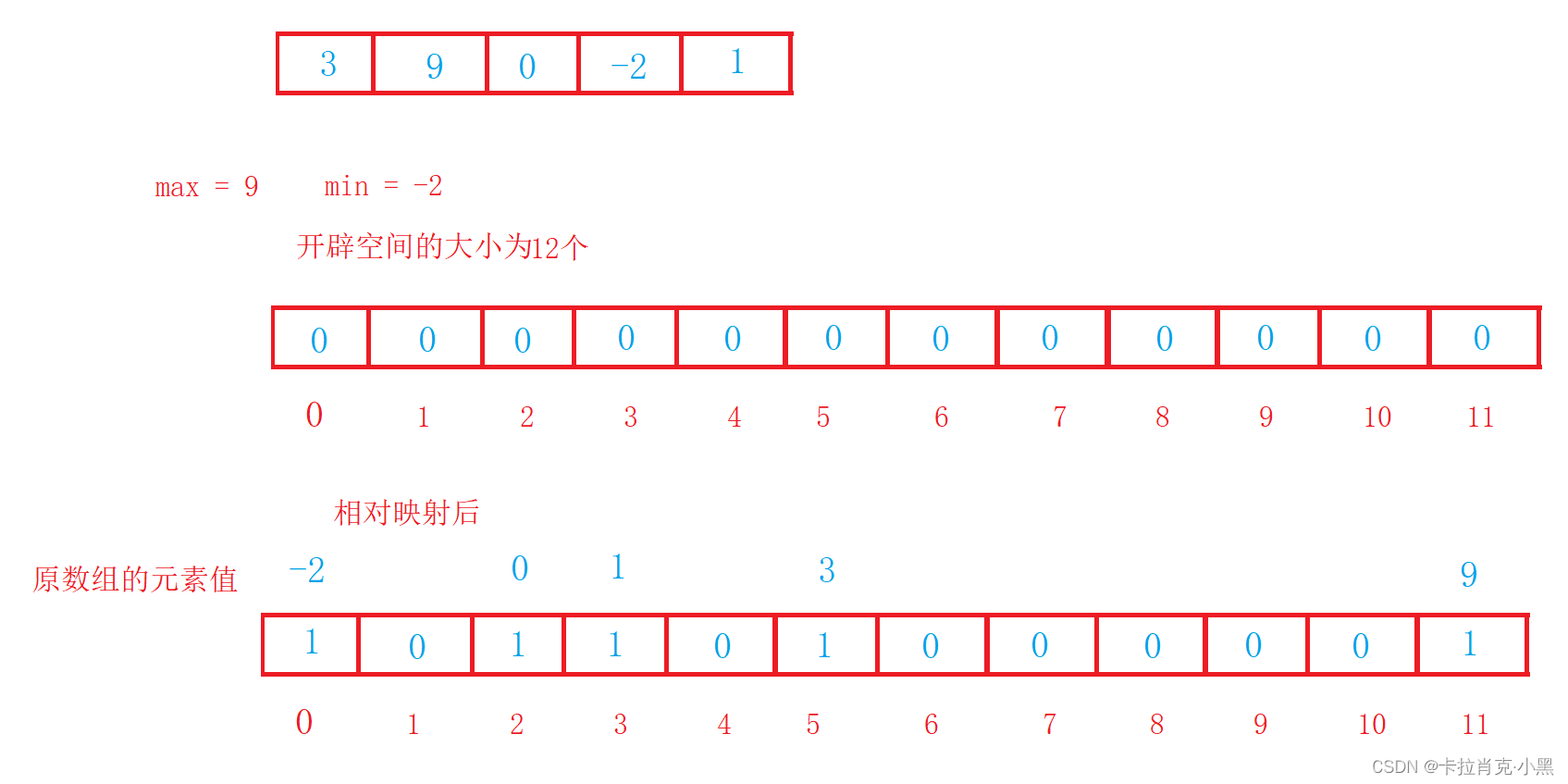
计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
二、排序算法复杂度及稳定性
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 空间消耗 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(N*logN)~O(N^2) | O(N^1.3) | O(N^2) | O(1) | 不稳定 |
| 冒泡排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 快速排序 | O(N*logN) | O(N*logN) | O(N^2) | O(N*logN)~O(N) | 不稳定 |
| 选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N*logN) | O(N*logN) | O(N*logN) | O(1) | 不稳定 |
| 归并排序 | O(N*logN) | O(N*logN) | O(N*logN) | O(N) | 稳定 |
排序测试
int tmp1[20];
int tmp2[20];
int tmp3[20];
int tmp4[20];
int tmp5[20];
int tmp6[20];
int tmp7[20];
int tmp8[20];
int tmp9[20];
int tmp10[20];
int tmp11[20];
int tmp12[20];
int tmp13[20];
void init()
{int i = 0;int nums = 0;for (i = 0; i < 20; i++){nums = rand() % 100;tmp1[i] = nums;tmp2[i] = nums;tmp3[i] = nums;tmp4[i] = nums;tmp5[i] = nums;tmp6[i] = nums;tmp7[i] = nums;tmp8[i] = nums;tmp9[i] = nums;tmp10[i] = nums;tmp11[i] = nums;tmp12[i] = nums;tmp13[i] = nums;}
}
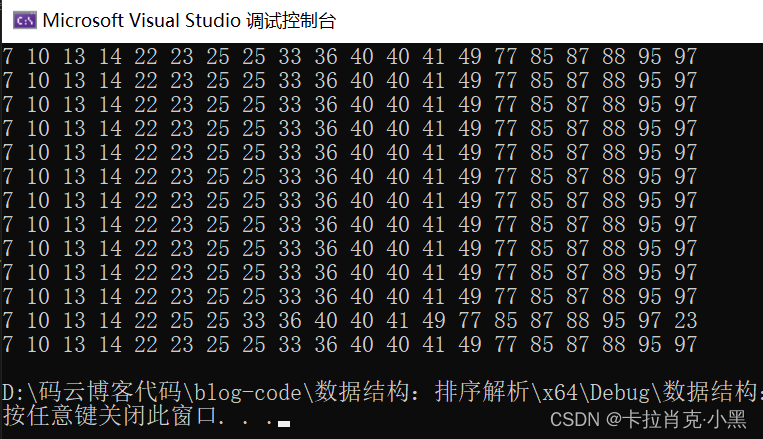
void test()
{int numsSize = 20;InsertSort(tmp1, numsSize);//插入排序ShellSort(tmp2, numsSize);//希尔排序BubbleSort(tmp3, numsSize);//冒泡排序PartSort1(tmp4, 0, numsSize - 1);//快排1PartSort2(tmp5, 0, numsSize - 1);//快排2PartSort3(tmp6, 0, numsSize - 1);//快排3QuickSort(tmp7, 0, numsSize - 1);//快排改进QuickSortNonR(tmp8, 0, numsSize - 1);//快排非递归SelectSort(tmp9, numsSize);HeapSort(tmp10, numsSize);int* tmp = (int*)malloc(sizeof(int) * numsSize);MergeSort(tmp11, 0, numsSize - 1, tmp);MergeSortNonR(tmp12, numsSize - 1, tmp);CountSort(tmp13, numsSize);free(tmp);
}
void print(int* nums, int numsSize)
{int i = 0;for (i = 0; i < numsSize; i++){printf("%d ", nums[i]);}printf("\n");
}
void Print()
{print(tmp1, 20);print(tmp2, 20);print(tmp3, 20);print(tmp4, 20);print(tmp5, 20);print(tmp6, 20);print(tmp7, 20);print(tmp8, 20);print(tmp9, 20);print(tmp10, 20);print(tmp11, 20);print(tmp12, 20);print(tmp13, 20);
}
int main()
{srand((unsigned)time());//int nums[] = { 3,9,0,-2,1 };//int numsSize = sizeof(nums) / sizeof(nums[0]);//计算数组大小//sortArray(nums, numsSize);//调用排序算法init();//对排序的数组赋值test();//调用各个排序函数//print(nums, numsSize);//打印排序结果Print();//打印各个排序结果return 0;
}
相关文章:

数据结构:排序解析
文章目录 前言一、常见排序算法的实现1.插入排序1.直接插入排序2.希尔排序 2.交换排序1.冒泡排序2.快速排序1.hoare版2.挖坑版3.前后指针版4.改进版5.非递归版 3.选择排序1.直接选择排序2.堆排序 4.归并排序1.归并排序递归实现2.归并排序非递归实现 5.计数排序 二、排序算法复杂…...
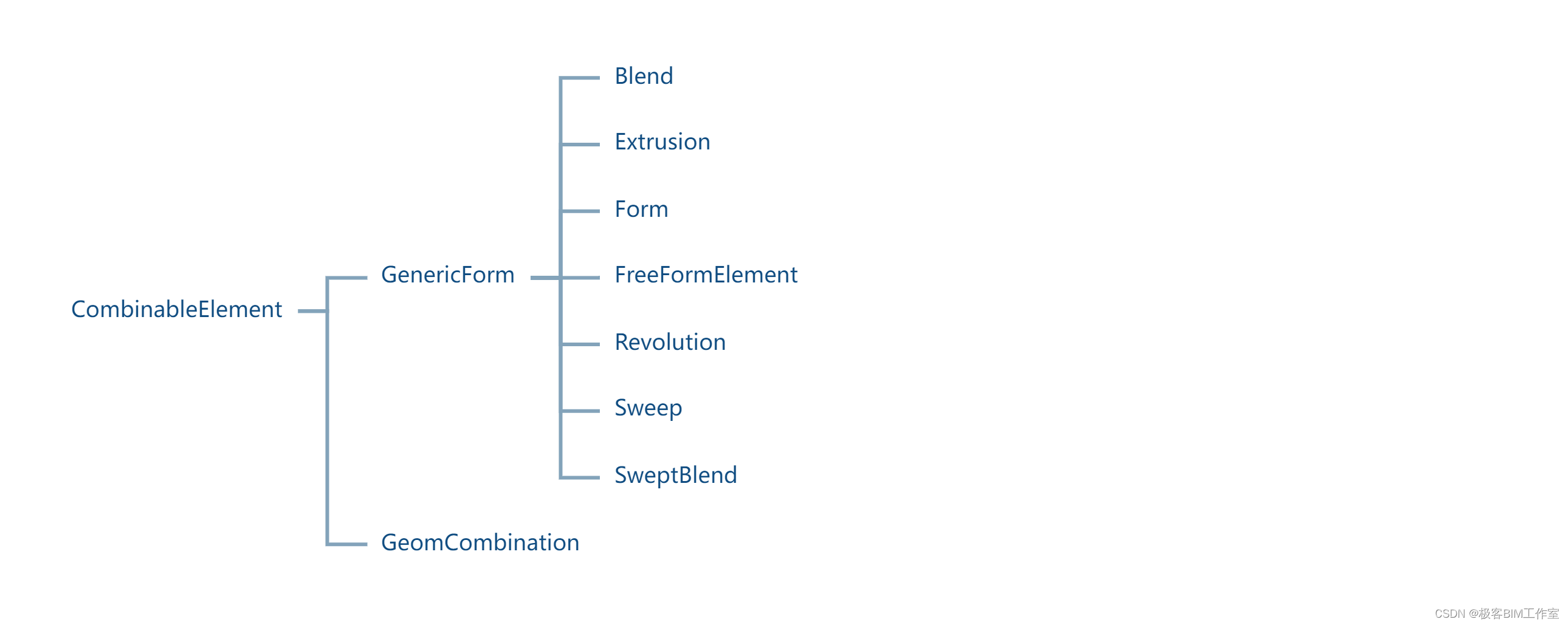
Revit SDK:AutoJoin 自动合并体量
前言 Revit 有一套完整的几何造型能力,每一个体量都是一个GenericForm,这些体量可以通过拉伸、扫掠等创建。这个例子介绍如何将他们合并成一个体量。 内容 合并体量的关键接口: // Autodesk.Revit.DB.Document public GeomCombination Com…...
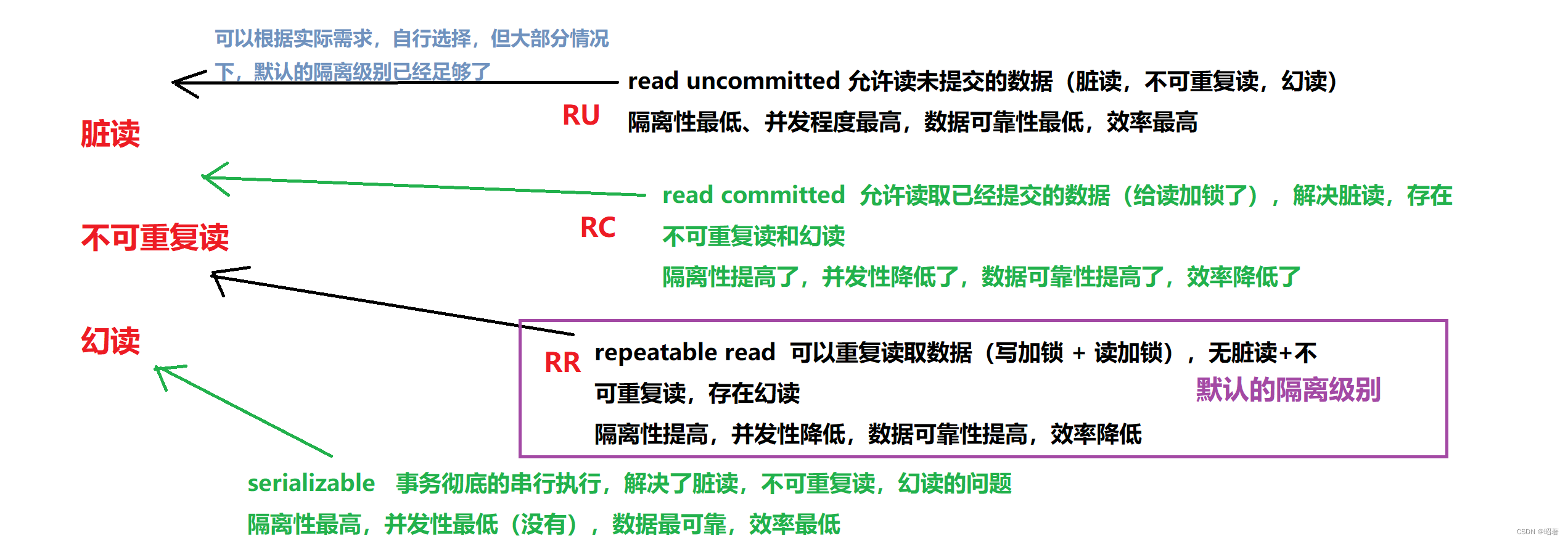
MYSQL(索引、事务)
文章目录 一、索引二、事务 一、索引 数据库中的表、数据、索引之间的关系,类似于书架上的图书、书籍内容和书籍目录的关系 1. 概述 概念:相当于是一本书的目录,是以‘列’为维度进行建立的使用场景:如果我们要查询一个表中的某个…...
设置Docker容器内的中文字符集,解决某些情况下中文乱码的问题)
部署问题集合(二十三)设置Docker容器内的中文字符集,解决某些情况下中文乱码的问题
前言: 同事给了一个服务,在Windows环境下怎么跑都正常,但一到Linux虚拟机里就中文乱码起初就想到了可能是字符集的问题,但调整了半天也没见效果,最后隔了几天突然想到,我是构建Docker跑的,而且…...

Web AP—PC端网页特效
PC端网页特效 代码下载 元素偏移量 offset 系列 offset 翻译过来就是偏移量, 我们使用 offset系列相关属性可以动态的得到该元素的位置(偏移)、大小等。 获得元素距离带有定位父元素的位置获得元素自身的大小(宽度高度&#x…...

Spring线程池ThreadPoolTaskExecutor使用
为什么使用线程池? 降低系统资源消耗,通过重用已存在的线程,降低线程创建和销毁造成的消耗;提高系统响应速度,当有任务到达时,通过复用已存在的线程,无需等待新线程的创建便能立即执行…...

spring mvc的执行流程
请求拦截。用户发起请求,请求先被sevlet拦截,转发给spring mvc框架请求转发。spring mvc里面的DispcherServlet会接收到请求并转发给HandlerMapping匹配接口。HandlerMapping负责解析请求,根据请求信息和配置信息找到匹配的controller类&…...
docker作业
目录 1、使用mysql:5.6和 owncloud 镜像,构建一个个人网盘。 1.1启动镜像 1.2启动cloud镜像 1.3浏览器访问 编辑 2、安装搭建私有仓库 Harbor 2.1下载docker-compose 2.2 磁盘挂载,保存harbor 2.3 修改配置文件 2.4安装 2.5浏览器访问 2.6 新…...

java实现本地文件转文件流发送到前端
java实现本地文件转文件流发送到前端 Controller public void export(HttpServletResponse response) {// 创建file对象response.setContentType("application/octet-stream");// 文件名为 sresponse.setHeader("Content-Disposition", "attachment;…...
2020ICPC南京站
K K Co-prime Permutation 题意:给定n和k,让你构造n的排列,满足gcd(pi, i)1的个数为k。 思路:因为x和x-1互质,1和任何数互质,任何数和它本身不互质 当k为奇数时,p11,后面k-1个数…...

Linux 中的 chsh 命令及示例
介绍 bash shell 是 Linux 最流行的登录 shell 之一。但是,对于不同的命令行操作,可以使用替代方法。chshLinux 中的( change shell )命令使用户能够修改登录 shell 。 以下教程...

JavaScript 数组如何实现冒泡排序?
冒泡排序是一种简单但效率较低的排序算法,常用于对小型数据集进行排序。它的原理是多次遍历数组,比较相邻元素的大小,并根据需要交换它们的位置,将最大(或最小)的元素逐渐“冒泡”到数组的一端。这个过程会…...

ZooKeeper集群环境搭建
🥇🥇【大数据学习记录篇】-持续更新中~🥇🥇 个人主页:beixi 本文章收录于专栏(点击传送):【大数据学习】 💓💓持续更新中,感谢各位前辈朋友们支持…...
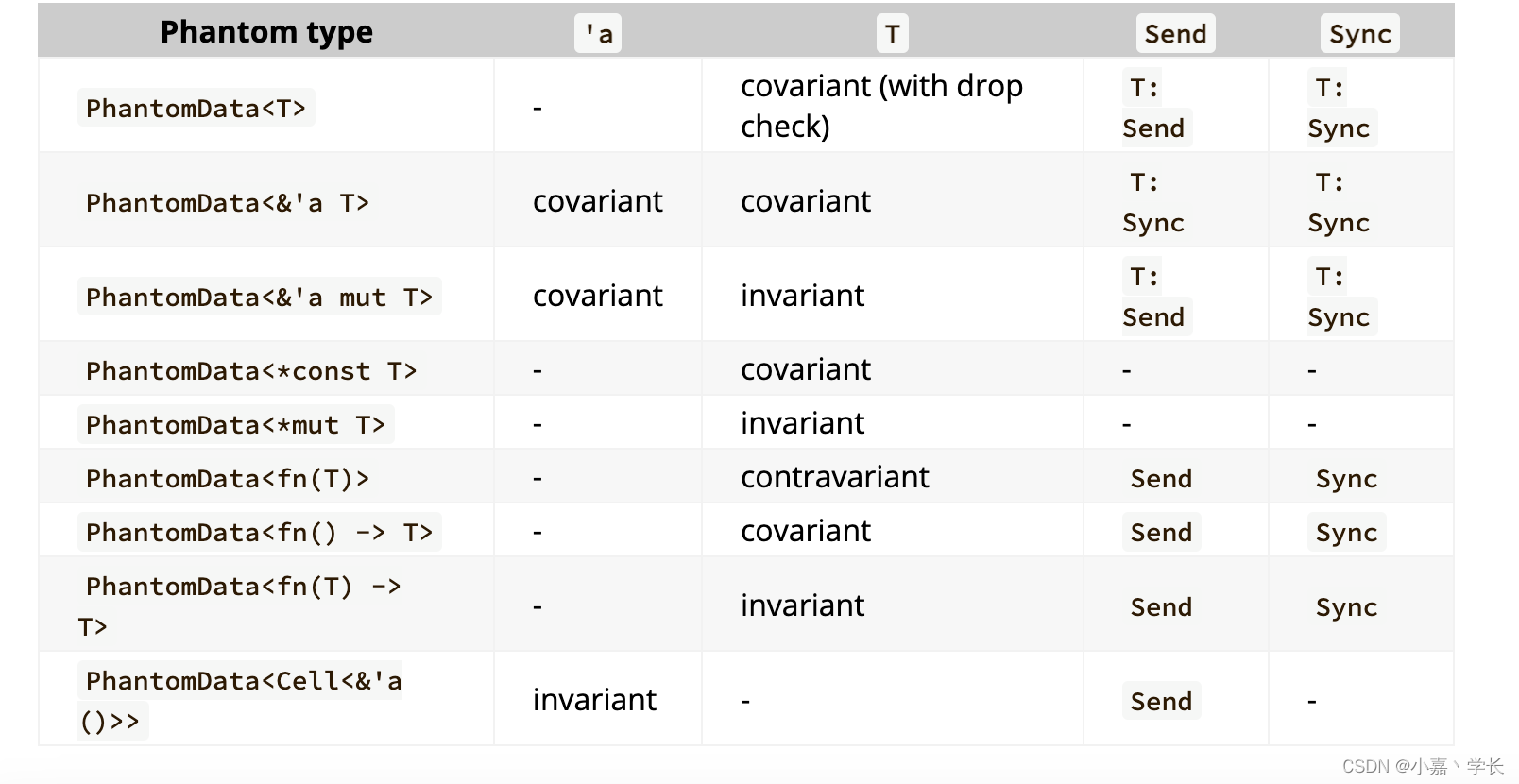
【跟小嘉学 Rust 编程】二十、进阶扩展
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...

pytorch学习过程中一些基础语法
1、tensor.view()函数,通俗理解就是reshape,#参数这里的-1需要注意,可以根据原张量size自行计算 data1torch.randn((4,2)) data2data1.view(2,4) data3data2.view(-1,8)2、tensor.max()函数,在分类问题中,通常需要使用…...

判断聚类 n_clusters
目录 基本原理 代码实现: 肘部法则(Elbow Method): 轮廓系数(Silhouette Coefficient) Gap Statistic(间隙统计量): Calinski-Harabasz Index(Calinski-…...

基于深度学习的网络异常检测方法研究
摘要: 本文提出了一种基于深度学习的网络异常检测方法,旨在有效地识别网络中潜在的异常行为。通过利用深度学习算法,结合大规模网络流量数据的训练,我们实现了对复杂网络环境下的异常行为的准确检测与分类。实验结果表明…...
SSM 基于注解的整合实现
一、pom.xml <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://maven.apache.org/maven-v4_0_0.xsd"><modelV…...

工具类APP如何解决黏性差、停留短、打开率低等痛点?
工具产品除了需要把自己的功能做到极致之外,其实需要借助一些情感手段、增设一些游戏机制、输出高质量内容、搭建社区组建用户关系链等方式,来提高产品的用户黏性,衍生产品的价值链。 工具类产品由于进入门槛低,竞争尤为激烈&…...

使用Java MVC开发高效、可扩展的Web应用
在当今的Web开发领域,高效和可扩展性是我们追求的目标。Java作为一种强大且广泛使用的编程语言,提供了丰富的工具和框架来支持Web应用的开发。其中,MVC模式是一种被广泛采用的架构模式,它能够有效地组织和管理代码,使得…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
