D360周赛复盘:模拟(思维题目)⭐⭐+贪心解决可能的最小和(类似上次)
文章目录
- 2833.距离原点最远的点
- 思路
- 完整版
- 2834.找出美丽数组的最小和
- 思路
- 完整版
2833.距离原点最远的点
给你一个长度为 n 的字符串 moves ,该字符串仅由字符 'L'、'R' 和 '_' 组成。字符串表示你在一条原点为 0 的数轴上的若干次移动。
你的初始位置就在原点(0),第 i 次移动过程中,你可以根据对应字符选择移动方向:
- 如果
moves[i] = 'L'或moves[i] = '_',可以选择向左移动一个单位距离 - 如果
moves[i] = 'R'或moves[i] = '_',可以选择向右移动一个单位距离
移动 n 次之后,请你找出可以到达的距离原点 最远 的点,并返回 从原点到这一点的距离 。
示例 1:
输入:moves = "L_RL__R"
输出:3
解释:可以到达的距离原点 0 最远的点是 -3 ,移动的序列为 "LLRLLLR" 。
示例 2:
输入:moves = "_R__LL_"
输出:5
解释:可以到达的距离原点 0 最远的点是 -5 ,移动的序列为 "LRLLLLL" 。
示例 3:
输入:moves = "_______"
输出:7
解释:可以到达的距离原点 0 最远的点是 7 ,移动的序列为 "RRRRRRR" 。
提示:
1 <= moves.length == n <= 50moves仅由字符'L'、'R'和'_'组成
思路
- 当
L_count>R_count时,字符串中向左的移动比向右的多。而每个 _ 可以视为一个“自由移动”,它可以选择向左或向右移动。为了到达原点最远的距离,所有的 _都应该选择向左移动。所以,abs(L_count - R_count) + _count就是最远的距离。
这个解法的核心思想是,为了达到最远的距离,应该尽可能地选择一个方向移动。
完整版
- 因为需要移动n次,所有的移动字符都需要被遍历。因此,我们需要将L的总数与R的总数相减,再加上自由步数。
class Solution {
public:int furthestDistanceFromOrigin(string moves) {int L_count = count(moves.begin(),moves.end(),'L');int R_count = count(moves.begin(),moves.end(),'R');int _count = count(moves.begin(),moves.end(),'_');return abs(L_count-R_count)+_count;}
};
2834.找出美丽数组的最小和
给你两个正整数:n 和 target 。
如果数组 nums 满足下述条件,则称其为 美丽数组 。
nums.length == n.nums由两两互不相同的正整数组成。- 在范围
[0, n-1]内,不存在 两个 不同 下标i和j,使得nums[i] + nums[j] == target。
返回符合条件的美丽数组所可能具备的 最小 和。
示例 1:
输入:n = 2, target = 3
输出:4
解释:nums = [1,3] 是美丽数组。
- nums 的长度为 n = 2 。
- nums 由两两互不相同的正整数组成。
- 不存在两个不同下标 i 和 j ,使得 nums[i] + nums[j] == 3 。
可以证明 4 是符合条件的美丽数组所可能具备的最小和。
示例 2:
输入:n = 3, target = 3
输出:8
解释:
nums = [1,3,4] 是美丽数组。
- nums 的长度为 n = 3 。
- nums 由两两互不相同的正整数组成。
- 不存在两个不同下标 i 和 j ,使得 nums[i] + nums[j] == 3 。
可以证明 8 是符合条件的美丽数组所可能具备的最小和。
示例 3:
输入:n = 1, target = 1
输出:1
解释:nums = [1] 是美丽数组。
提示:
1 <= n <= 1051 <= target <= 105
思路
本题就和上次周赛的贪心很像了,求得也是可能的最小和,所以需要从最小的数字开始取!
完整版
和上次周赛代码基本相同,求的都是可能的最小和问题。
class Solution {
public:long long minimumPossibleSum(int n, int target) {set<long long>used;int cur = 1;long long sum=0;for(int i=1;i<=n;i++){while(used.count(cur)||used.count(target-cur)){cur++;}used.insert(cur);sum+=cur;}return sum;}
};
相关文章:
⭐⭐+贪心解决可能的最小和(类似上次))
D360周赛复盘:模拟(思维题目)⭐⭐+贪心解决可能的最小和(类似上次)
文章目录 2833.距离原点最远的点思路完整版 2834.找出美丽数组的最小和思路完整版 2833.距离原点最远的点 给你一个长度为 n 的字符串 moves ,该字符串仅由字符 L、R 和 _ 组成。字符串表示你在一条原点为 0 的数轴上的若干次移动。 你的初始位置就在原点…...

【C++学习】函数指针
#include<iostream> //包含头文件 using namespace std; void func(int no, string str){cout << "亲爱的"<< no << "号:" << str << endl; }int main(){int bh 3;string message "我是一只傻傻鸟";func…...

A. Copil Copac Draws Trees
Problem - 1830A - Codeforces 问题描述: 科皮尔-科帕克(Copil Copac)得到一个由 n − 1 n-1 n−1条边组成的列表,该列表描述了一棵由 n n n个顶点组成的树。他决定用下面的算法来绘制它: 步骤 0 0 0:…...

D359周赛复盘:贪心解决求最小和问题⭐⭐+较为复杂的双层线性DP⭐⭐
文章目录 2828.判别首字母缩略词完整版 2829.k-avoiding数组的最小总和(贪心解法)思路完整版 类似题:2834.找出美丽数组的最小和思路完整版 2830.销售利润最大化⭐⭐思路DP数组含义递推公式 完整版 2828.判别首字母缩略词 给你一个字符串数组…...
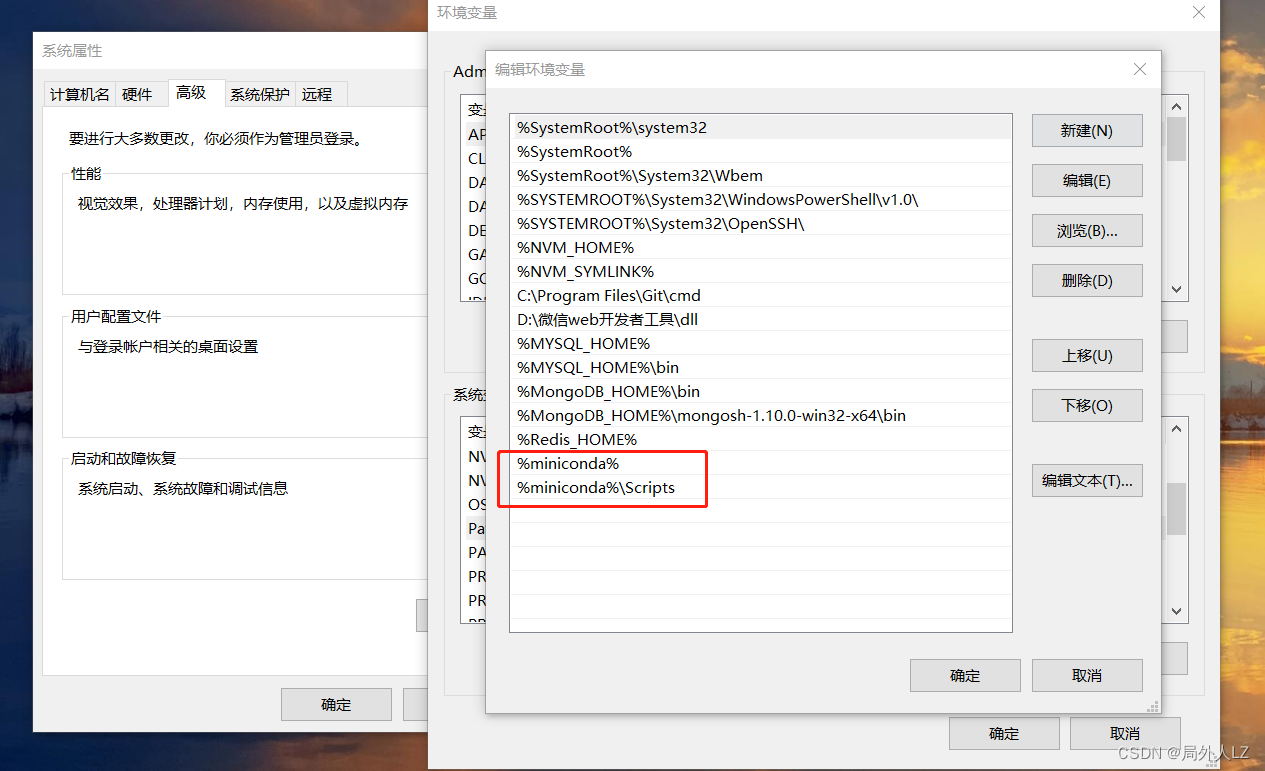
python基础之miniConda管理器
一、介绍 MiniConda 是一个轻量级的 Conda 版本,它是 Conda 的精简版,专注于提供基本的环境管理功能。Conda 是一个流行的开源包管理系统和环境管理器,用于在不同的操作系统上安装、管理和运行软件包。 与完整版的 Anaconda 相比,…...

C++算法 —— 分治(1)快排
文章目录 1、颜色分类2、排序数组3、第k个最大的元素(快速选择)4、最小的k个数(快速选择) 分治,就是分而治之,把大问题划分成多个小问题,小问题再划分成更小的问题。像快排和归并排序就是分治思…...

接口用例设计
章节目录: 一、针对输入设计1.1 数值型1.2 字符串型1.3 数组或链表类型 二、针对业务逻辑2.1 约束条件分析2.2 操作对象分析2.3 状态转换分析2.4 时序分析 三、针对输出设计3.1 针对输出结果3.2 接口超时 四 、其他测试设计4.1 已废弃接口测试4.2 接口设计合理性分析…...

Selenium超级详细的教程
Selenium是一个用于自动化测试的工具,它可以模拟用户在浏览器中的各种操作。除了用于测试,Selenium还可以用于爬虫,特别是在处理动态加载页面时非常有用。本文将为您提供一个超级详细的Selenium教程,以帮助您快速入门并了解其各种…...
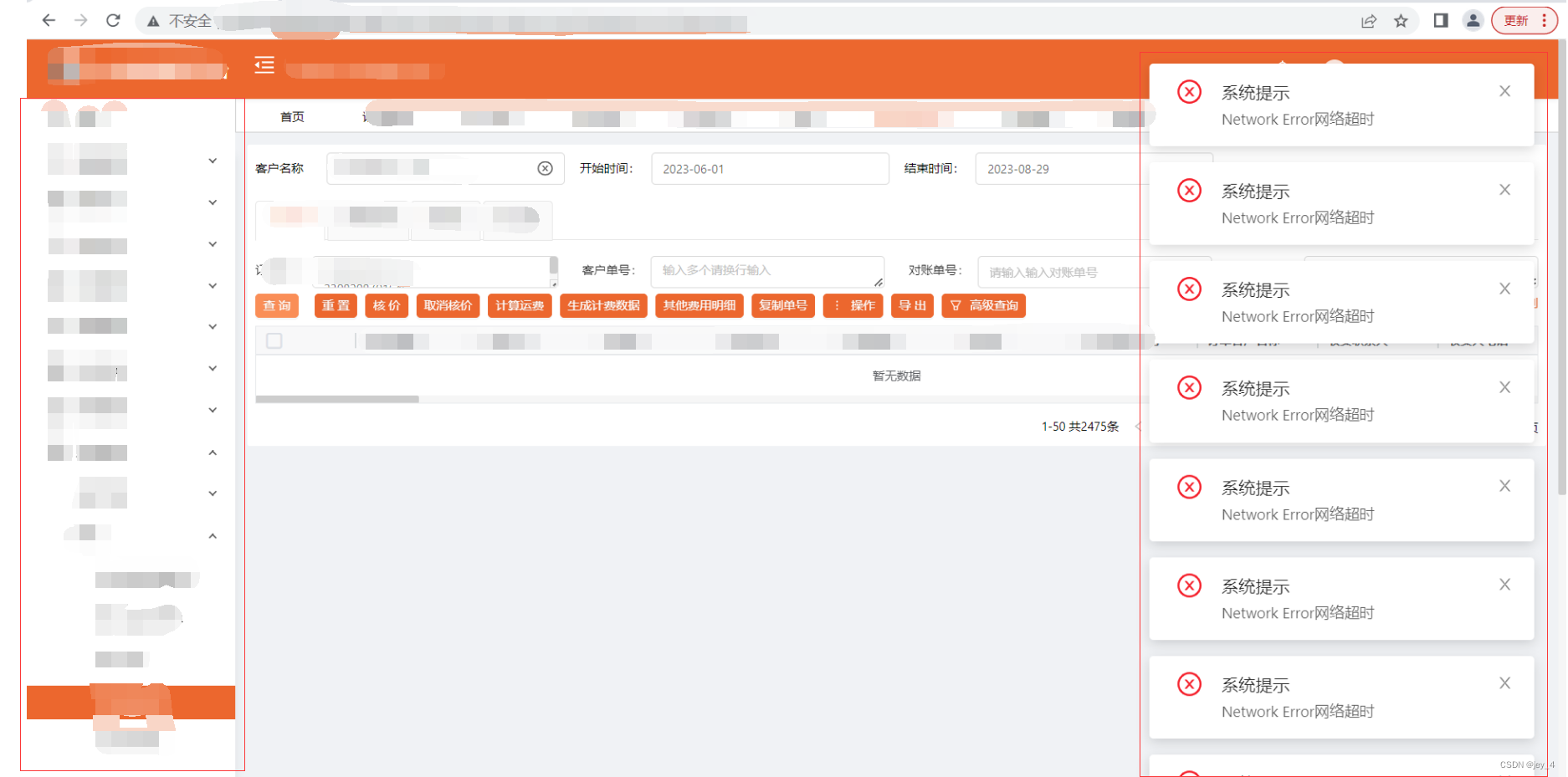
服务报network error错误
问题:服务请求时会偶发性的报【network error网络超时】(请求瞬间就报) 可能原因: 服务器linux内核调优时将:net.ipv4.tcp_tw_recycle设置为1,开启TCP连接中TIME-WAIT sockets的快速回收,默认为…...

【ES6】利用 Proxy实现函数名链式效果
利用 Proxy,可以将读取属性的操作(get),转变为执行某个函数,从而实现属性的链式操作。 var pipe function (value) {var funcStack [];var oproxy new Proxy({} , {get : function (pipeObject, fnName) {if (fnNa…...
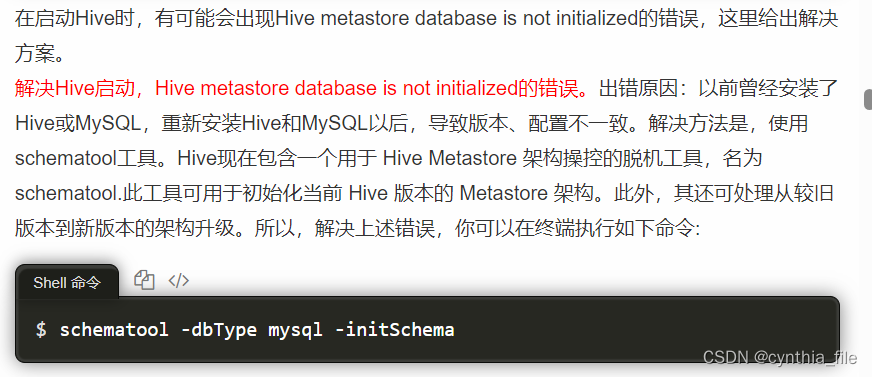
hive部署
下载hive安装包:https://dlcdn.apache.org/hive/hive-2.3.9/解压及环境部署 tar -zxvf apache-hive-2.3.9-bin.tar.gz mv apache-hive-2.3.9-bin hivevim /etc/profile添加至环境变量 export HIVE_HOME/usr/local/hive export PATH$PATH:$HIVE_HOME/binsource /etc…...

ip白名单之网段
代码托管,有时候为了安全性,限制网段内的ip可以访问。 IP地址和掩码均知道时才能确定主机所在的网段,也就是用这个原理来限制可访问的IP网段了。 ip后面加上“/N”就代表掩码的二进制”1“有N位。 例如: ①0.0.0.0/0 主机ip地…...
PMP项目管理主要学习内容是什么?
PMP项目管理是指根据美国项目管理学会(Project Management Institute,简称PMI)制定的项目管理知识体系和方法论进行项目管理的一种认证。PMP主要关注项目的规划、执行和控制等方面的知识和技能。 下面是PMP项目管理《PMBOK指南》第六版的主要学习内容: …...
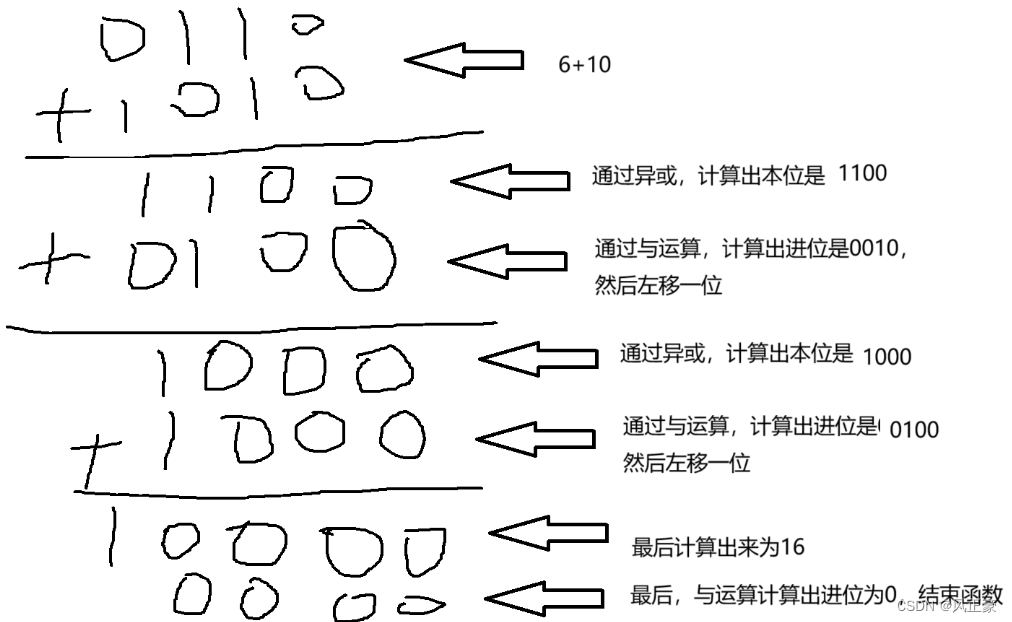
小米面试题——不用加减乘除计算两数之和
前言 (1)刷B站看到一个面试题,不用加减乘除计算两数之和。 (2)当时我看到这个题目,第一反应就是感觉这是一个数电题目。不过需要采用C语言的方式编写出来。 (3)不过看到大佬的代码之…...

Mysql 日志管理 数据备份
MySQL日志管理 MySQL的默认日志保存位置为/usr/local/mysql/data 日志开启方式有两种:通过配置文件或者是通过命令 通过命令修改开启的日志是临时的,关闭或重启服务后就会关闭 日志的分类 1.错误日志 用来记录当MySQL启动、停止或运行时发生的错误信…...

Java小记-腾讯2020校招-后台-逛街
题目描述: 小Q在周末的时候和他的小伙伴来到大城市逛街,一条步行街上有很多高楼,共有n座高楼排成一行。 小Q从第一栋一直走到了最后一栋,小Q从来都没有见到这么多的楼,所以他想知道他在每栋楼的位置处能看到多少栋楼呢…...
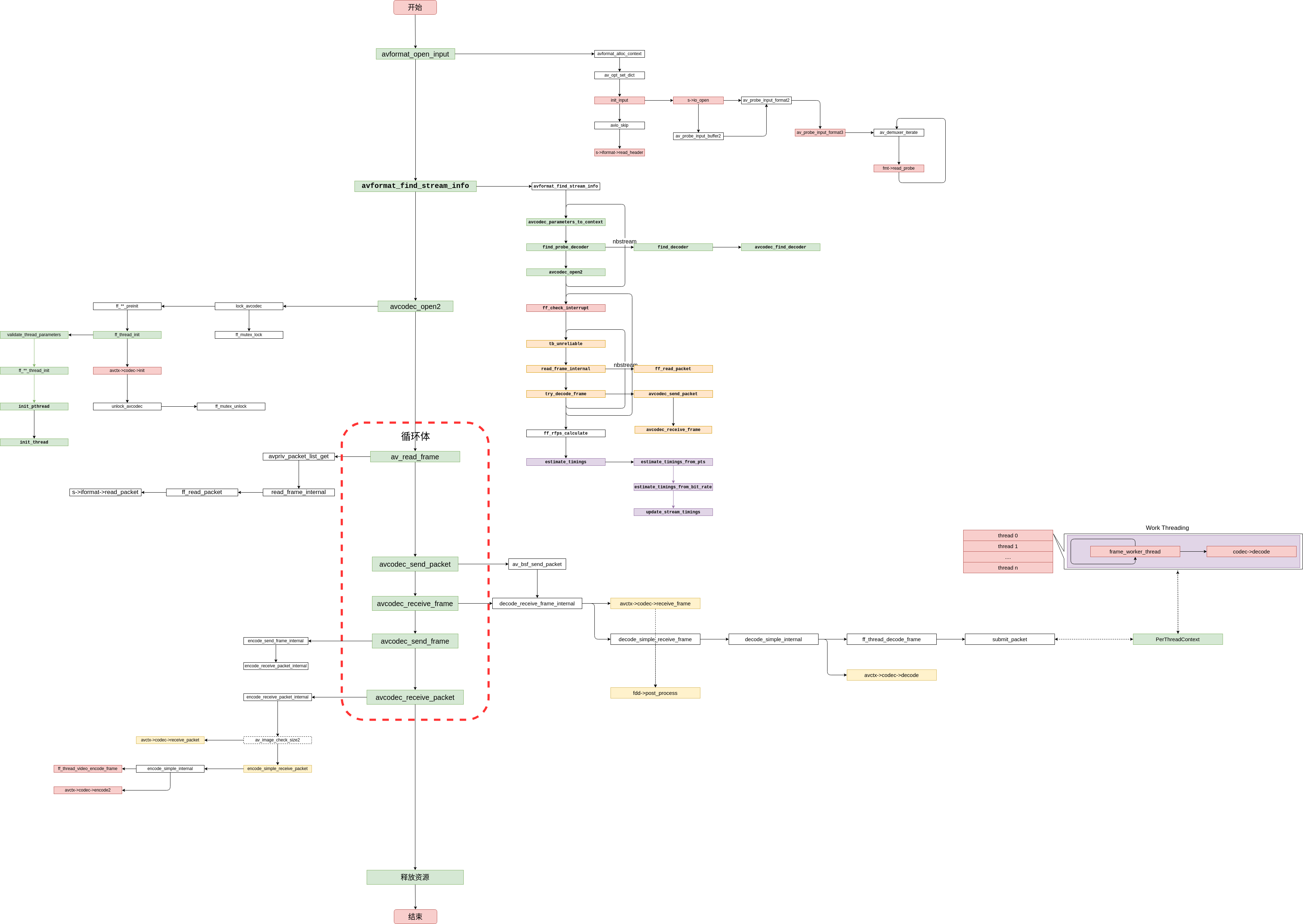
FFmpeg5.0源码阅读——FFmpeg大体框架
摘要:前一段时间熟悉了下FFmpeg主流程源码实现,对FFmpeg的整体框架有了个大概的认识,因此在此做一个笔记,希望以比较容易理解的文字描述FFmpeg本身的结构,加深对FFmpeg的框架进行梳理加深理解,如果文章中有…...

【算法刷题之字符串篇】
目录 1.leetcode-344. 反转字符串(1)方法:双指针 2.leetcode-541. 反转字符串 II(1)方法一:模拟(2)方法二:双指针 3.leetcode-剑指 Offer 05. 替换空格(1&…...

js中forEach和map的区别:forEach不会改变原数组,而map会改变数组?错了错了
1.提出思考?forEach不会改变原数组,而map会改变数组? 看到掘金上一篇文章觉得很有意思:大致是描述一般面试官问js中forEach和map的区别?都会回答forEach不会改变原数组,而map会改变,我也一直对…...

深度对话:从底层看Sui设计理念及网络规模扩展
近日,我们采访了George Danezis以了解Sui的交易处理系统如何促成高性能网络。他是Mysten Labs的联合创始人和首席科学家(Sui的最初贡献者),也是伦敦大学学院(University College London,UCL)安全…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...

使用VMware克隆功能快速搭建集群
自己搭建的虚拟机,后续不管是学习java还是大数据,都需要集群,java需要分布式的微服务,大数据Hadoop的计算集群,如果从头开始搭建虚拟机会比较费时费力,这里分享一下如何使用克隆功能快速搭建一个集群 先把…...

【向量库】Weaviate 搜索与索引技术:从基础概念到性能优化
文章目录 零、概述一、搜索技术分类1. 向量搜索:捕捉语义的智能检索2. 关键字搜索:精确匹配的传统方案3. 混合搜索:语义与精确的双重保障 二、向量检索技术分类1. HNSW索引:大规模数据的高效引擎2. Flat索引:小规模数据…...

C++ 使用 ffmpeg 解码 rtsp 流并获取每帧的YUV数据
一、简介 FFmpeg 是一个开源的多媒体处理框架,非常适用于处理音视频的录制、转换、流化和播放。 二、代码 示例代码使用工作线程读取rtsp视频流,自动重连,支持手动退出,解码并将二进制文件保存下来。 注意: 代…...
