【面试经典150题】多数元素
🔗题目链接
✈题目描述:
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
⌊ n/2 ⌋表示n/2结果向下取整。
🚆数据范围:
n == nums.length1 <= n <= 5 * 104-109 <= nums[i] <= 109
🍁思路分析:
因为 ⌊ n 2 ⌋ ≤ n 2 < ⌊ n 2 ⌋ + 1 \lfloor \frac{n}{2} \rfloor \le \frac{n}{2} < \lfloor \frac{n}{2} \rfloor + 1 ⌊2n⌋≤2n<⌊2n⌋+1,所以这个 多数元素 至多只有1个。
🖊解法1:
使用一个辅助对象计数,遍历数组,如果有一个元素的次数超过了 ⌊ n/2 ⌋,即为结果。
/*** @param {number[]} nums* @return {number}*/
var majorityElement = function(nums) {let count={};let flag=Math.floor(nums.length/2);for(let i=0;i<nums.length;i++){if(count[nums[i]]===undefined){count[nums[i]]=0;}count[nums[i]]++;if(count[nums[i]]>flag){return nums[i];}}
};
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ) O(n) O(n)
🖊解法2:
由于多数元素的个数大于其他所有元素总和,所以我们可以从头维护一个候选元素,同时给其计数,遇到同类元素+1,遇到异类元素-1,减为0时,再维护当前元素,再重复之前步骤。
/*** @param {number[]} nums* @return {number}*/
var majorityElement = function(nums) {let candidate=nums[0];let count=1;for(let i=1;i<nums.length;i++){if(count===0){candidate=nums[i];count=1;}else if(candidate===nums[i]){count++;}else{count--;}}return candidate;
};
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
相关文章:

【面试经典150题】多数元素
🔗题目链接 ✈题目描述: 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 ⌊ n/2 ⌋表示n/2结果向下取…...
)
c#垃圾回收(Garbage Collection)
在C#中,垃圾回收(Garbage Collection)是一种自动管理内存的机制。它负责跟踪和释放不再使用的内存,以便程序可以有效地使用内存资源。 C#中的垃圾回收器是由.NET运行时(CLR)提供和管理的。它使用了一种叫做…...

vue 基于element-plus el-button封装按钮组件
封装组件的原则是:组件只是数据流通的一个管道,不要糅合太多的逻辑在里面,是一个纯组件,还要根据自己项目的业务场景做具体的处理。 // MyButton.vue // 基于element-plus中el-button来封装按钮 <template><el-button c…...

smbus只能再python2.7下运行?不能再python3.8下运行吗?
不是的,SMBus并不只能在Python 2.7下运行,它也可以在Python 3.8及更高版本下运行。SMBus是用于访问系统上的I2C设备(Inter-Integrated Circuit,一种串行通信协议)的Python库,它应该与Python 3.8兼容。 要在…...

python中is和==的区别
is 和 的区别 在Python中,is和是两个用于比较对象的操作符,它们有不同的作用和用法。 is操作符: is用于比较两个对象的身份标识,即判断两个对象是否引用同一个内存地址的对象。当is操作符用于比较两个对象时,它会判断…...
Viobot回环使用
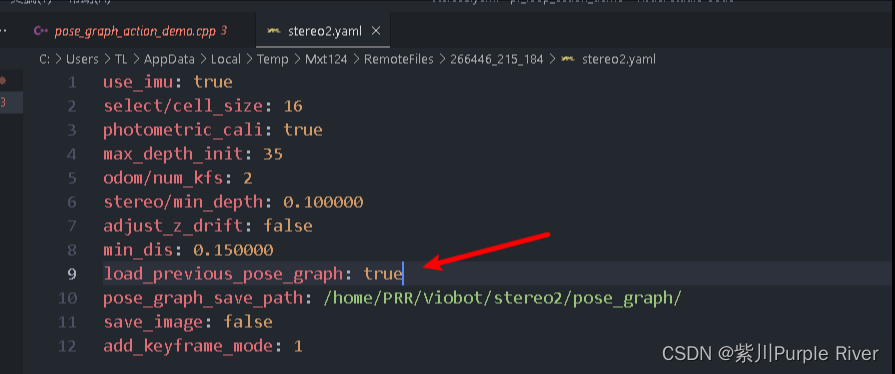
Viobot回环是使用词袋匹配的方式,,当新的关键帧能够匹配词袋里面记录过的关键帧时,触发回环,将设备的当前位姿拉到历史位姿。 一.上位机操作 词袋使用方法 连接上设备,先停止算法。UI上点 设置 选到 loop 选项卡&…...

React钩子函数之forward结合useImperativeHandle钩子的基本使用
React钩子函数是React框架中非常重要的一部分,其中forward和useImperativeHandle是两个常用的钩子函数。这两个钩子函数可以结合使用,用来实现一些高级的功能。 首先,让我们来了解一下forward钩子函数。它的作用是将父组件中的props传递给子…...

c++中移动语义和完美转发
C 中的移动语义和完美转发是 C11 引入的两个重要特性,它们分别用于提高性能和灵活性。 移动语义(Move Semantics): 移动语义允许有效地将资源(如堆上分配的内存或其他资源)从一个对象转移到另一个对象,而…...

【linux命令讲解大全】040. 文件操作:使用touch命令创建和更新文件
文章目录 touch补充说明语法选项参数示例 从零学 python touch 创建新的空文件或更新已存在文件的时间标签。 补充说明 touch命令具有两个功能: 更新已存在文件的时间标签为当前系统时间(默认方式),文件的数据保持不变。创建新…...

Redis之MoreKey问题及Scan命令解读
目录 MoreKey问题讨论 Scan命令 Sscan命令 Hscan命令 Zscan命令 MoreKey问题讨论 keys * 查看当前库所有key 对于海量数据执行key *会造成严重服务卡顿、影响业务。在实际环境中最好不要使用。生产制造过程中keys * / flushdb/flushall等危险命令以防止误删误用。 大量的…...
QA工具开发流程
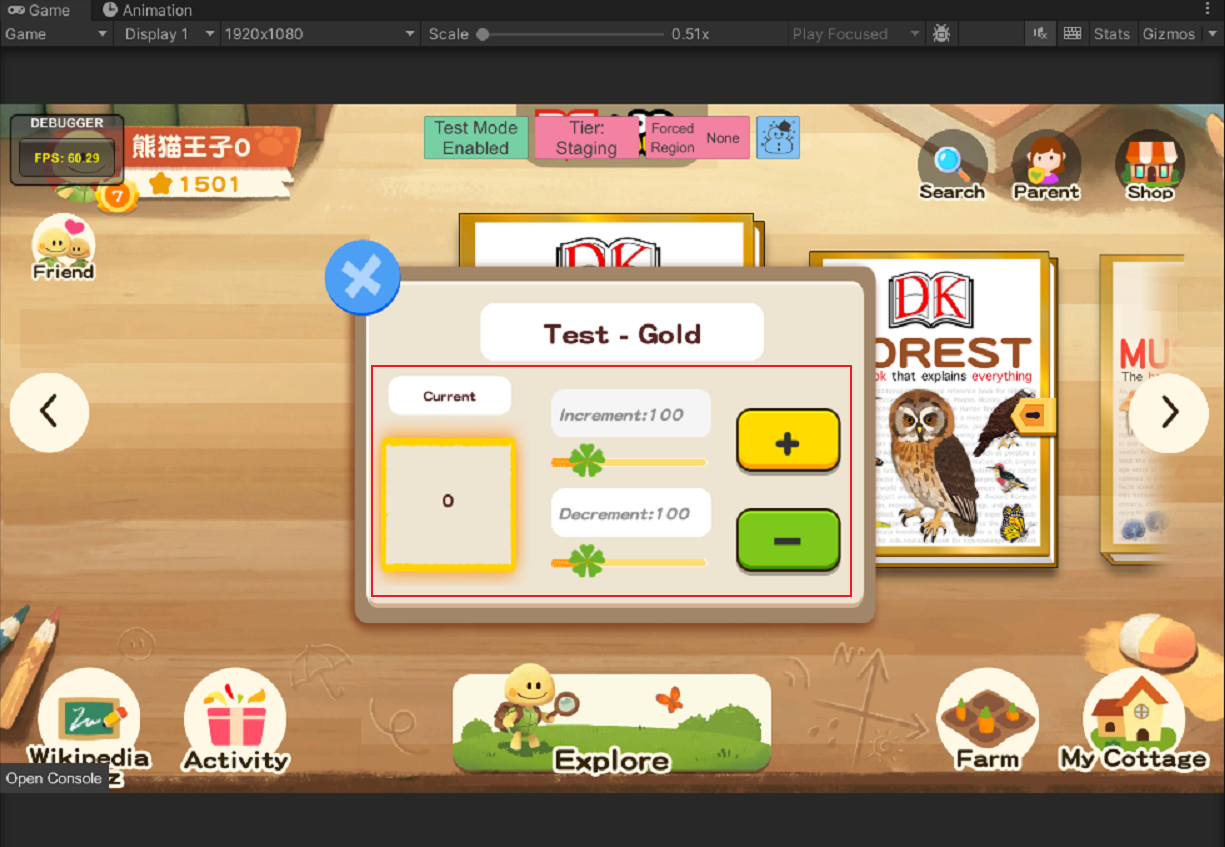
前言 在项目上线前期,这边根据需求制作了一套QA测试工具。主要分为以下四个模块的测试**图1** **数值测试:**主要包括了角色的等级变更、游戏里货币的变更、(目前已制作的)游戏道具的数量变更。这些可能归一为一类测试模型**动画…...

JSON.toJSONString首字母大小写问题
前言 开发过程中遇到的,对象转字符串时,有个字段首字母是大写的,转换之后就变成了小写,在这里记录下 代码示例 String jsonString JSON.toJSONString(obj,SerializerFeature.PrettyFormat,SerializerFeature.WriteMapNullValue,…...

ant-vue1.78版a-auto-complete表单自动搜索返回列表中的关键字标红
a-auto-complete表单自动搜索返回列表中的关键字标红 通常在做关键字标红的场景,都是后端返回html结构,前端直接渲染实现,但是如果需要前端处理的话,实现也是很简单的,接下来我直接上应用场景吧 应用场景就是通过关键…...
Elasticsearch 优化
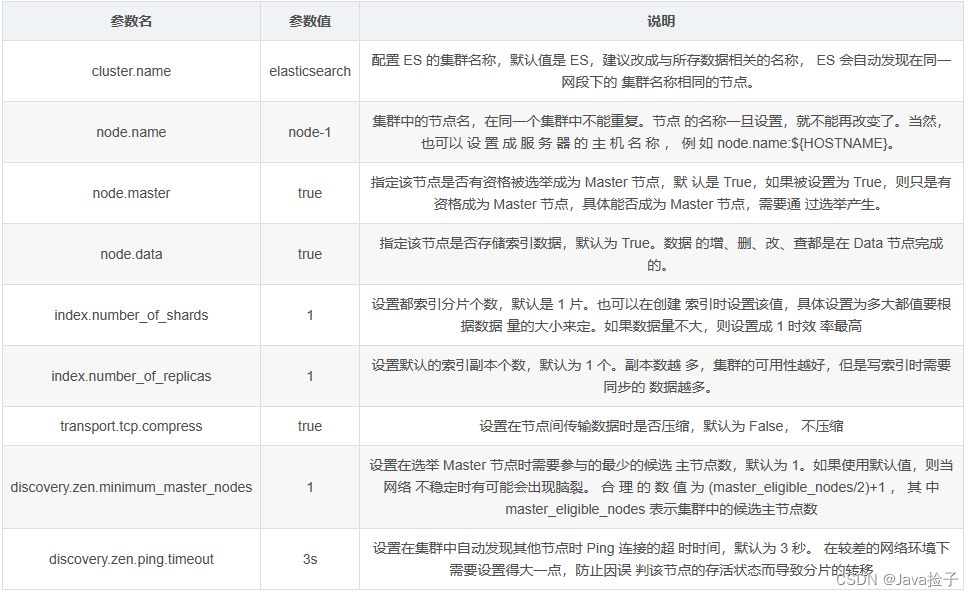
Elasticsearch 优化 2.1硬件选择 Elasticsearch 的基础是 Lucene ,所有的索引和文档数据是存储在本地的磁盘中,具体的 路径可在 ES 的配置文件 ../config/elasticsearch.yml 中配置,如下: #----------------------------…...

spring boot的自动装配原理
spring boot的自动装配原理 解释和使用关键技术思想总结 解释和使用 自动装配是什么:自动将第三方组件的bean装载到ioc容器里,不需要开发人员再去写bean相关的一些配置 spring boot怎么做:在启动类上加SpringBootApplication注解就可以实现自…...

走进低代码平台| iVX-困境之中如何突破传统
前言: “工欲善其事,必先利其器”,找到和使用一个优质的工具平台,往往会事半功倍。 文章目录 1️⃣认识走近低代码2️⃣传统的低代码开发3️⃣无代码编辑平台一个代码生成式低代码产品iVX受面性广支持代码复用如何使用? 4️⃣总结…...

【UIPickerView案例03-点餐系统之随机点餐 Objective-C语言】
一、先来看看我们这个示例程序里面,随机点餐是怎么做的 1.点击:“随机点餐”按钮 大家能想到,它是怎么实现的吗 1)首先,点击”随机点餐“按钮,的时候,你要让这个pickerView,进行随机选中,那么,得监听它的点击 2)然后呢,让pickeView选中数据, 3)然后呢,把那个…...

论文阅读_扩散模型_SDXL
英文名称: SDXL: Improving Latent Diffusion Models for High-Resolution Image Synthesis 中文名称: SDXL:改进潜在扩散模型的高分辨率图像合成 论文地址: http://arxiv.org/abs/2307.01952 代码: https://github.com/Stability-AI/generative-models 时间: 2023-…...
云原生Kubernetes:二进制部署K8S多Master架构(三)
目录 一、理论 1.K8S多Master架构 2.配置master02 3.master02 节点部署 4.负载均衡部署 二、实验 1.环境 2.配置master02 3.master02 节点部署 4.负载均衡部署 三、总结 一、理论 1.K8S多Master架构 (1) 架构 2.配置master02 (1)环境 关闭防…...

任意文件读取和下载
任意文件读取是什么? 一些网站的需求,可能会提供文件查看与下载的功能。如果对用户查看或下载的文件没有限制或者限制绕就可以查看或下载任意文件。这些文件可以是源代码文件配置文件敏感文件等等。过, 任意文件读取会造成(敏感)信息泄露;任意…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
