算法通关村14关 | 堆在数组中找第k大的元素应用
1. 在数组中找第k大元素
题目
LeetCode215:给定整数数组nums和整数k,请返回数组中第k个最大的元素,

思路
解题思路用三个,选择法,堆查找和快速排序。
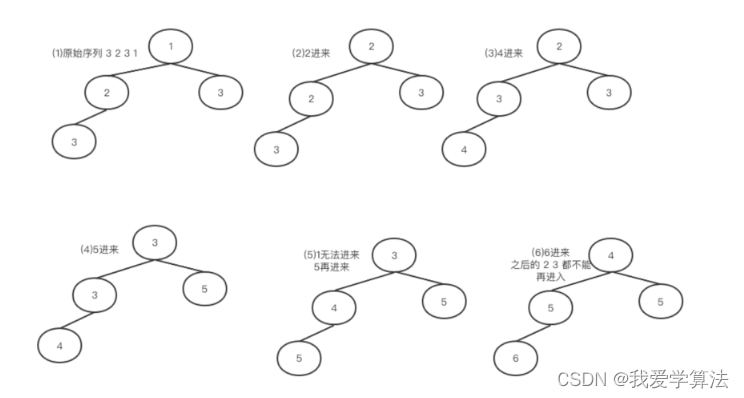
我们选择用大堆小堆解决问题,“找最大用小堆,找最小用大堆,找中间用两个堆”,我们构造一个大小只有4的小根堆,为了更好的说明情况,我们扩展一下题目序列[3,2,3,1,2,4,5,1,5,6,2,3]。
堆满了之后,只有大于根节点的元素才能入堆,否则就直接抛弃,元素进入堆中,需要调换位置,满足最小堆的结构,如果发现两个子树都小,则应该和最小的元素交换,如果都一样,则随便选一个。
需要注意:堆不满则直接添加;堆满的时候读到大于根节点的元素才将堆顶拿出,放入新读到的数。
代码
我们用的是Javajdk中的PriorityQueue构建最小堆
/*** 用最小堆在数组中找第k大的元素* @param nums* @param k* @return*/public int findkLargest(int[] nums, int k){if (k > nums.length){return -1;}int len = nums.length;//创建一个含有k个元素的最小堆PriorityQueue<Integer> minHeap = new PriorityQueue<>(k,(a,b) -> (a - b));for (int i = 0; i < k; i++) {minHeap.add(nums[i]);}for (int i = 0; i < len; i++) {Integer topEle = minHeap.peek();//只要比堆顶大的元素,最顶弹出,遍历的元素进去if (nums[i] > topEle){minHeap.poll();minHeap.offer(nums[i]);}}return minHeap.peek();}相关文章:

算法通关村14关 | 堆在数组中找第k大的元素应用
1. 在数组中找第k大元素 题目 LeetCode215:给定整数数组nums和整数k,请返回数组中第k个最大的元素, 思路 解题思路用三个,选择法,堆查找和快速排序。 我们选择用大堆小堆解决问题,“找最大用小堆ÿ…...
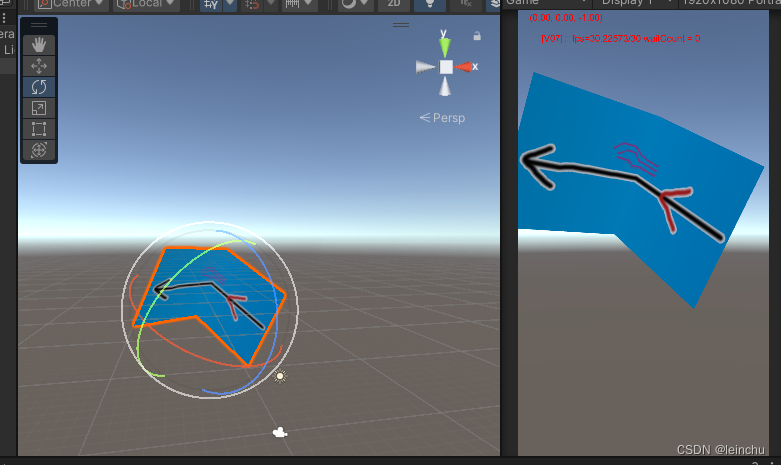
Unity 顶点vertices,uv,与图片贴图,与mesh
mesh就是组成3d物体的三角形们。 mesh由顶点组成的三角形组成,三角形的大小 并不 需要一样,由顶点之间的位置决定。 mesh可以是一个或者多个面。 贴图的原点在左下角,uv是贴图的坐标,数量和顶点数一样(不是100%确定…...

Shell编程之函数
目录 基本概念 自定义函数 系统函数 1.read 2.basename 3.dirname 基本概念 将一段代码组合封装在一起实现某个特定的功能或返回某个特定的值,然后给这段代码取个名字,也就是函数名,在需要实现某个特定功能的时候直接调用函数名即可。 函…...

10.物联网LWIP之TCP状态转变
一。TCP状态机 1.青粗线:理想TCP状态转变(服务器视角下) 2.虚线:被动TCP状态转变(服务器视角下) 3.细实线:不经常出现的TCP状态转变(类似于边界处理) 1.青粗线解释--》服…...

Img标签的src地址自动拼接本地域名(localhost:8080)导致图片不显示问题
摘要:做Vueelement ui项目的时候,发现使用element ui的upload上传图片时,不显示的问题。我项目的图片是上传到七牛云,长传成功后返回存储在七牛云中的地址。后面发现是因为返回的地址是外部地址,需要完整的URL…...

数据结构入门 — 栈
本文属于数据结构专栏文章,适合数据结构入门者学习,涵盖数据结构基础的知识和内容体系,文章在介绍数据结构时会配合上动图演示,方便初学者在学习数据结构时理解和学习,了解数据结构系列专栏点击下方链接。 博客主页&am…...
Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录
Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录 目录 Unity Android 之 在Unity 中引入 OkHttp的操作注意(OKHttp4.xx- kotlin 的包)简单记录 一、简单介绍 二、OKHttp 4.xx 的 SDK 封装 aar 给 Unity 的使用注意 三、附录 OKHttp 的…...

内嵌功能强大、低功耗STM32WB55CEU7、STM32WB55CGU7 射频微控制器 - MCU, 48-UFQFN
一、概述: STM32WB55xx多协议无线和超低功耗器件内嵌功能强大的超低功耗无线电模块(符合蓝牙 低功耗SIG规范5.0和IEEE 802.15.4-2011标准)。该器件内含专用的Arm Cortex -M0,用于执行所有的底层实时操作。这些器件基于高性能Arm …...

【测试】笔试03
文章目录 1. 哪种测试模型把测试过程作为需求分析、概要设计、详细设计及编码之后的阶段( )2. 在下面所列举的逻辑测试覆盖中,测试覆盖最强的是?3. 网络管理员编写了shell程序prog1.sh,测试时程序死循环无法结束,可以通过下列方式…...

JavaScript的while和for循环
一、循环语句 1.认识循环 在开发中我们经常需要做各种各样的循环操作: 比如把一个列表中的商品、歌曲、视频依次输出进行展示;比如对一个列表进行累加计算;比如运行相同的代码将数字 1 到 10 逐个输出; 循环 是一种重复运行同…...

mqtt安卓客户端
1.MQTT(消息队列遥测传输协议),是一种基于 发布/订阅 (publish/subscribe)模式的"轻量级"通讯协议, 该协议构建于TCP/IP协议上 。MQTT最大优点在于,可以以极少的代码和有限的带宽&…...
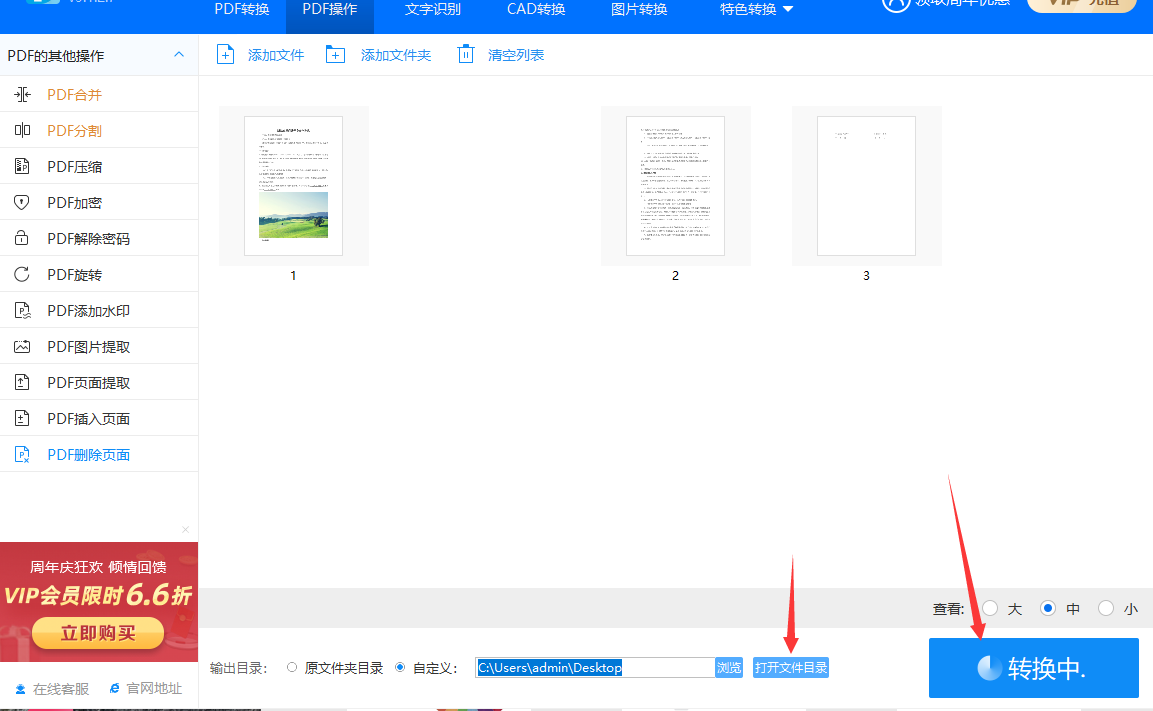
pdf怎么删除其中一页?
pdf怎么删除其中一页?现在,pdf文件已经深入影响着我们的工作和学习,如果你是一个上班族,那么几乎每天都会使用到pdf格式的电脑文件。当我们阅读一个页数众多的PDF文件时,可能会发现实际上只需要其中的一小部分内容。很…...
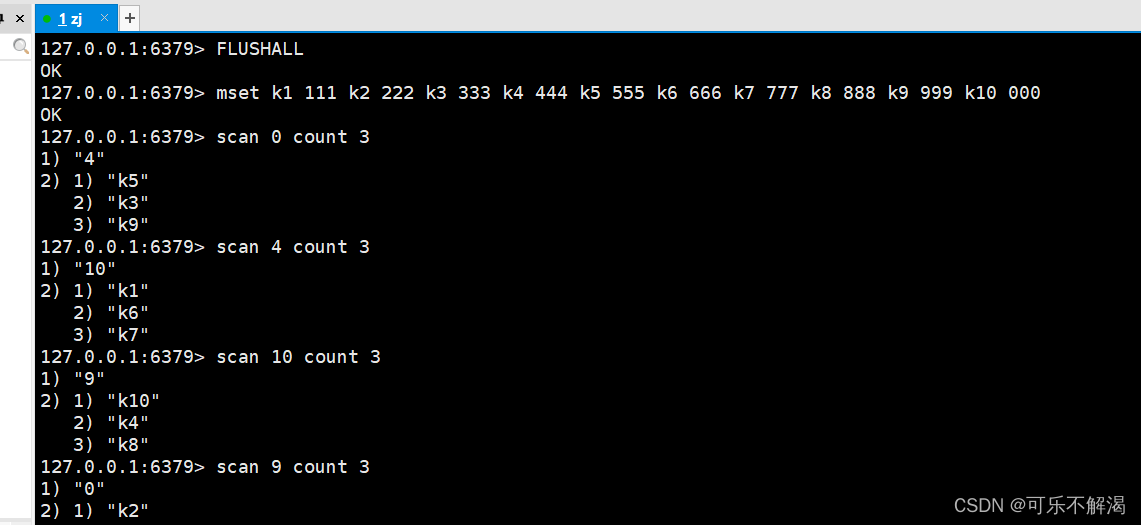
10.Redis 渐进式遍历
Redis 渐进式遍历 渐进式遍历scan 渐进式遍历 keys 命令一次性的把整个redis中所有的key都获取到,keys *但这个操作比较危险,可能会一下子得到太多的key,阻塞 redis 服务器。 通过渐进式遍历,就可以做到,既可以获取到所有的 key&…...
)
字符函数和字符串函数(2)
目录 memcpy memmove memcmp memcpy void * memcpy ( void * destination, const void * source, size_t num ); 1.函数memcpy从source的位置开始向后复制num个字节的数据到destination的内存位置。 2.这个函数在遇到 \0 的时候并不会停下来。 3.如果source和destination有…...

目录扫描+JS文件中提取URL和子域+403状态绕过+指纹识别(dirsearch_bypass403)
dirsearch_bypass403 在安全测试时,安全测试人员信息收集中时可使用它进行目录枚举,目录进行指纹识别,枚举出来的403状态目录可尝试进行绕过,绕过403有可能获取管理员权限。不影响dirsearch原本功能使用 运行流程 dirsearch进行…...
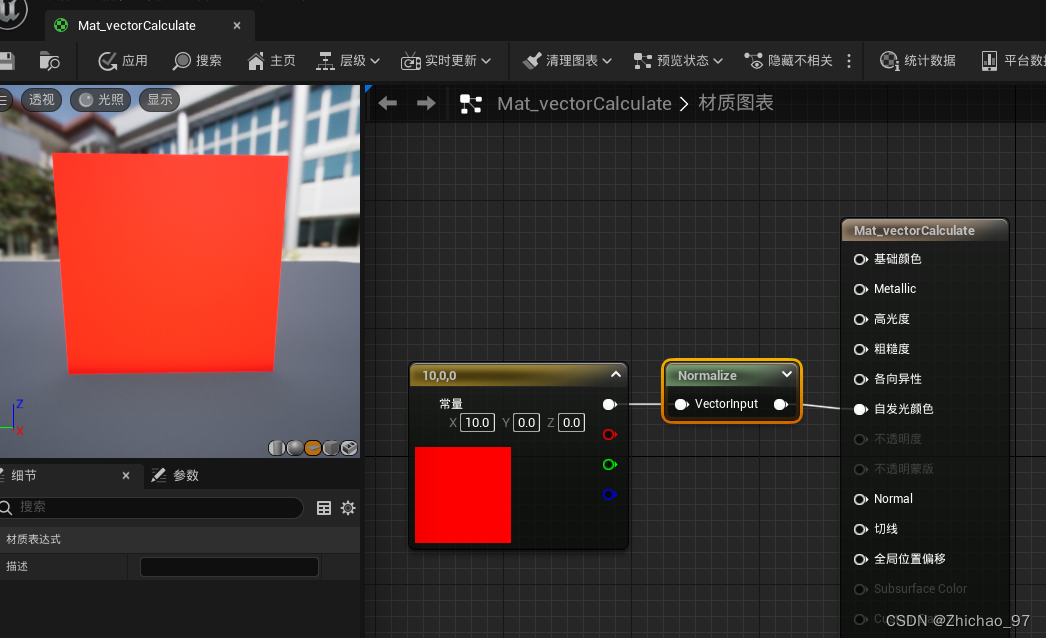
【UE 材质】常用向量运算节点——点积、叉积、归一化
目录 一、点积 二、叉积 三、归一化 一、点积 点积,也称为内积或数量积,是一种用于计算两个向量之间关系的操作。对于两个三维向量 A(a1,a2,a3)和 B(b1,b2,b3),它们的点积可以用以下公式表示: ABa1⋅…...

音视频 ffmpeg命令提取PCM数据
提取PCM ffmpeg -i buweishui.mp3 -ar 48000 -ac 2 -f s16le 48000_2_s16le ffmpeg -i buweishui.mp3 -ar 48000 -ac 2 -sample_fmt s16 out_s16.wav ffmpeg -i buweishui.mp3 -ar 48000 -ac 2 -codec:a pcm_s16le out2_s16le.wav ffmpeg -i buweishui.mp3 -ar 48000 -ac 2 -f…...

【MySQL】实现可扩展性:构建高性能的系统
什么是可扩展性?可扩展性的好处扩展方式纵向扩展(Scaling Up)横向扩展(Scaling Out) 总结 💯感谢 💖 什么是可扩展性? 可扩展性是指系统能够在需要时轻松地适应更多的工作负载和资源…...

网站用户体验之深度感悟
个性化定制界面和极简版原装界面,哪一个你用起来更加顺手呢,相比之下你更喜欢哪一个? 界面选择: (提醒:仅个人感悟。~~) 方向一:表明自己的喜好 我个人觉得更喜欢个性化定制界面。…...

目标检测YOLO实战应用案例100讲-道路场景下目标检测与分割模型的压缩研究与实现
目录 前言 目标检测方法 语义分割方法 相关理论基础 2.1 YOLO目标检测算法介绍...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
