解释 Git 的基本概念和使用方式(InsCode AI 创作助手)
Git 是一种分布式版本控制系统,它允许多个用户协同工作并对项目进行版本控制。下面是 Git 的基本概念和使用方式:
基本概念:
-
仓库(Repository):存储代码和版本历史记录的地方。
-
提交(Commit):在仓库中记录一次代码更改的操作。
-
分支(Branch):在代码仓库中,可以创建独立的分支来开发新功能或修复错误。
-
合并(Merge):将分支代码合并回主分支。
-
冲突(Conflict):当多个用户修改同一行代码时,可能会出现冲突。
使用方式:
-
创建仓库:使用 git init 命令创建一个新仓库。
-
添加文件:使用 git add 命令添加文件到暂存区。
-
提交更改:使用 git commit 命令将更改提交到仓库。
-
创建分支:使用 git branch 命令创建新分支。
-
切换分支:使用 git checkout 命令切换到另一个分支。
-
合并分支:使用 git merge 命令将分支合并到主分支。
-
解决冲突:当出现冲突时,需要手动解决冲突并提交更改。
-
拉取最新代码:使用 git pull 命令从远程仓库拉取最新代码。
-
推送更改:使用 git push 命令将本地更改推送到远程仓库。
Git 是一个非常强大的版本控制系统,可以帮助团队协作开发和管理代码,同时也是一个必备的工具。
相关文章:
)
解释 Git 的基本概念和使用方式(InsCode AI 创作助手)
Git 是一种分布式版本控制系统,它允许多个用户协同工作并对项目进行版本控制。下面是 Git 的基本概念和使用方式: 基本概念: 仓库(Repository):存储代码和版本历史记录的地方。 提交(Commit&a…...

【QT】信号和槽(15)
前面的内容说了很多不同的控件如何使用,今天来看下QT的核心,信号与槽(Signals and slots)! 简单理解一下,就是我们的信号与槽连接上了之后,发射一个信号给到槽,槽函数接收到了这个信…...
)
EFLK日志平台(filebeat-->kafka-->logstash-->es-->kiabana)
ELK平台是一套完整的日志集中处理解决方案,将 ElasticSearch、Logstash 和 Kiabana 三个开源工具配合使用, 完成更强大的用户对日志的查询、排序、统计需求。 安装顺序 1.安装es 7.17.12 2.安装kibana 7.17.12 3.安装x-pack 保证以上调试成功后开始下面…...
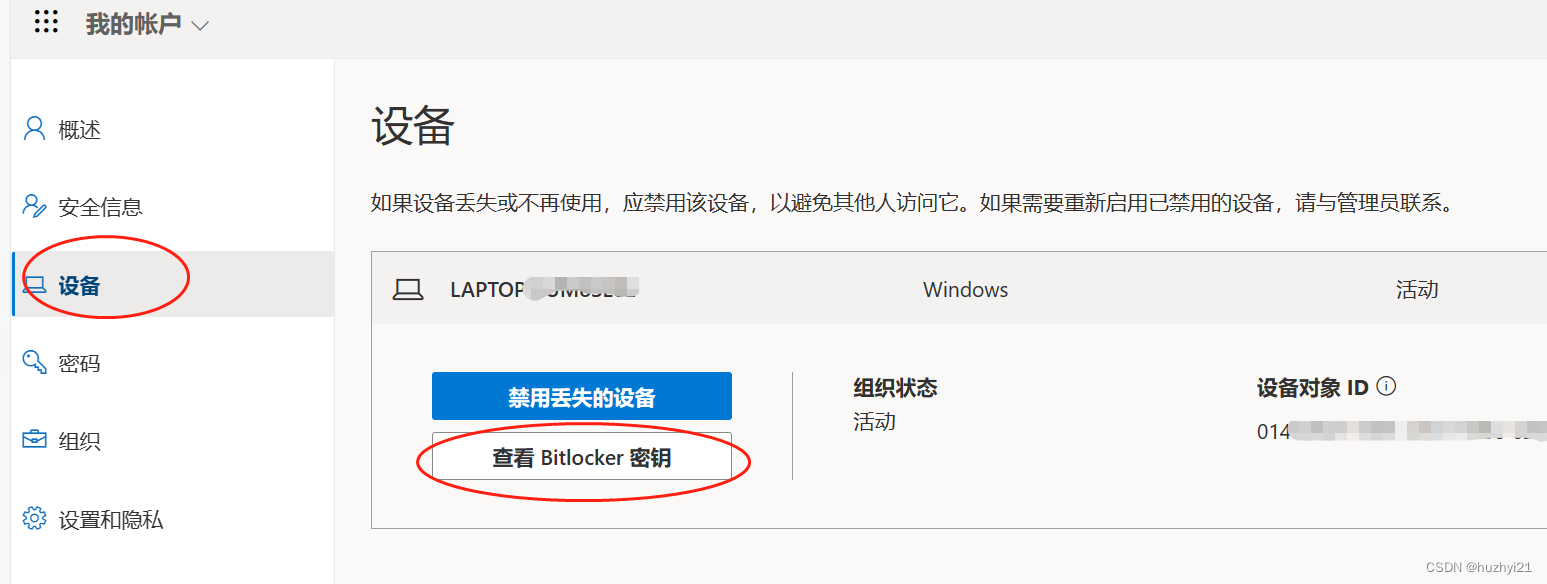
C盘扩容遇到的问题(BitLocker解密、)
120G的C盘不知不觉的就满了,忍了好久终于要动手了。 尽管电脑-管理--磁盘管理里可以进行磁盘大小调整,但由于各盘都在用,不能够连续调整,所以选用DiskGenius。 # DiskGenius调整分区大小遇到“您选择的分区不支持无损调整容量” …...
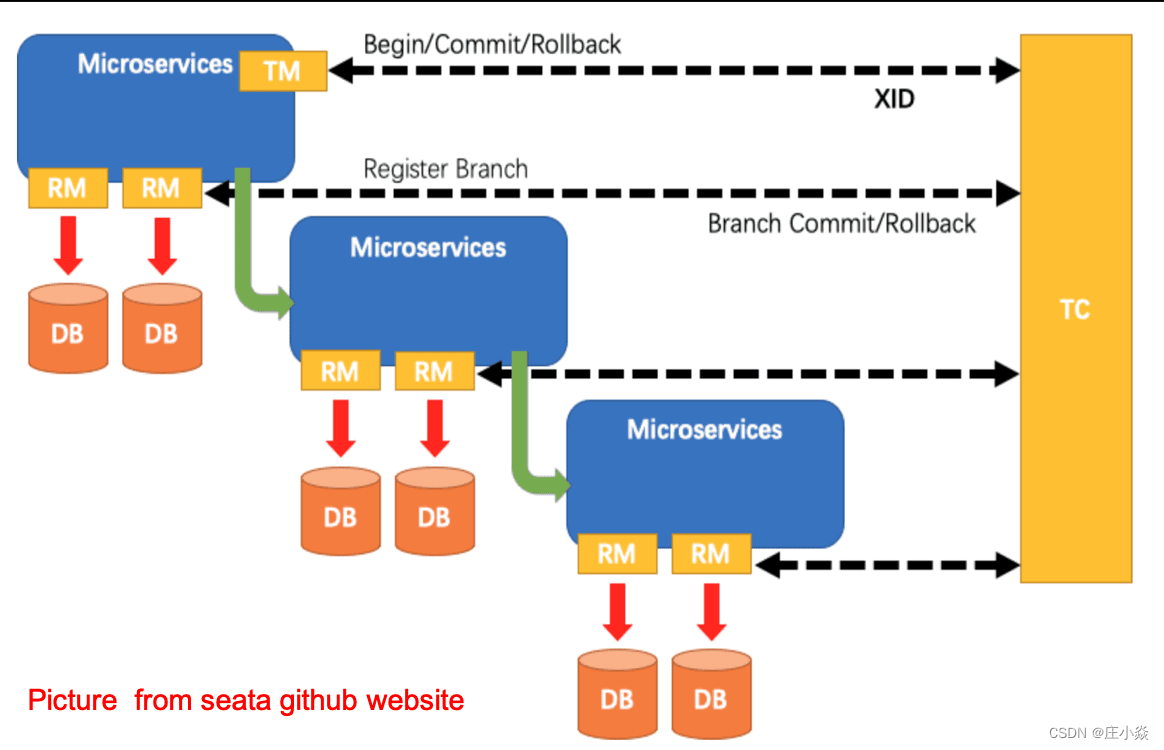
ShardingSphere——柔性事务SEATA原理
摘要 Apache ShardingSphere集成了 SEATA 作为柔性事务的使用方案,本文主要介绍其实现ShardingSphere中柔性事务SEATA原理原理。帮助你更好的理解ShardingSphere原理。同时帮助大家更好的使用柔性事务SEATA原理。 一、Seata柔性事务 Apache ShardingSphere 集成了…...
)
Introducing GlobalPlatform(一篇了解GP)
安全之安全(security)博客目录导读 TEE之GP(Global Platform)认证汇总 目录 一、GP简介 二、GP新的重点领域是什么? 三、认证程序和培训<...

Ubuntu 18.04上无法播放MP4格式视频解决办法
ubuntu18.04系统无法播放MP4格式视频,提示如下图所示: 解决办法: 1、首先,确保ubuntu系统已完全更新。可使用以下命令更新软件包列表:sudo apt update,然后使用以下命令升级所有已安装的软件包:…...

科技驱动产业升级:浅谈制造型企业对MES系统的应用
在科技不断进步的背景下,制造型行业也在持续发展,但随之而来的挑战也不断增加。传统的管理方式已经无法满足企业的需求,因此许多制造型企业开始寻找新的管理模式。制造执行系统(MES)作为先进的制造信息技术之一&#x…...
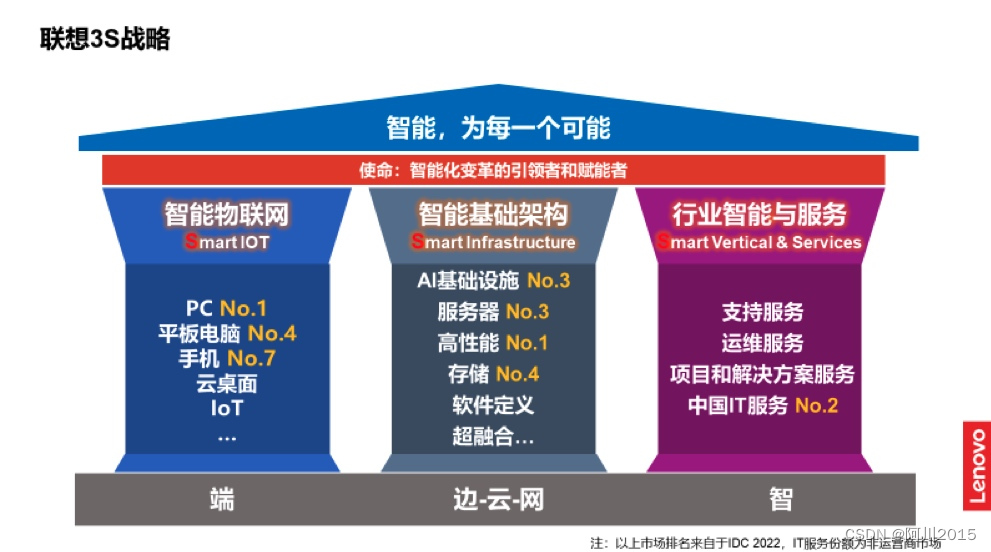
智能化新十年,“全栈智能”定义行业“Copilot智能助手”
“智能化转型是未来十年中国企业穿越经济周期的利器”,这是联想集团执行副总裁兼中国区总裁刘军在去年联想创新科技大会上做出的判断,而2023年正值第四次工业革命第二个十年的开端,智能化是第四次工业革命的主题。2023年初,基于谷…...

Docker资源控制cgroups
文章目录 一、docker资源控制1、资源控制工具2、Cgroups四大功能 二、CPU 资源控制1、设置CPU使用率上限2、CPU压力测试3、Cgroups限制cpu使用率4、设置CPU资源占用比(设置多个容器时才有效)5、设置容器绑定指定的CPU 三、对内存使用的限制四、对磁盘IO配…...

通过python 获取当前局域网内存在的IP和MAC
通过python 获取当前局域网内存在的ip 通过ipconfig /all 命令获取局域网所在的网段 通过arp -d *命令清空当前所有的arp映射表 循环遍历当前网段所有可能的ip与其ping一遍建立arp映射表 for /L %i IN (1,1,254) DO ping -w 1 -n 1 192.168.3.%i 通过arp -a命令读取缓存的映射表…...

解决D盘的类型不是基本,而是动态的问题
一、正确的图片 1.1图片 1.2本人遇到的问题 二、将动态磁盘 转为基本盘 2.1 基本概念,动态无法转化为基本,不是双向的,借助软件 网址:转换动态磁盘到普通磁盘_检测到计算机本地磁盘为动态分区_卫水金波的博客-CSDN博客 2.2分区…...
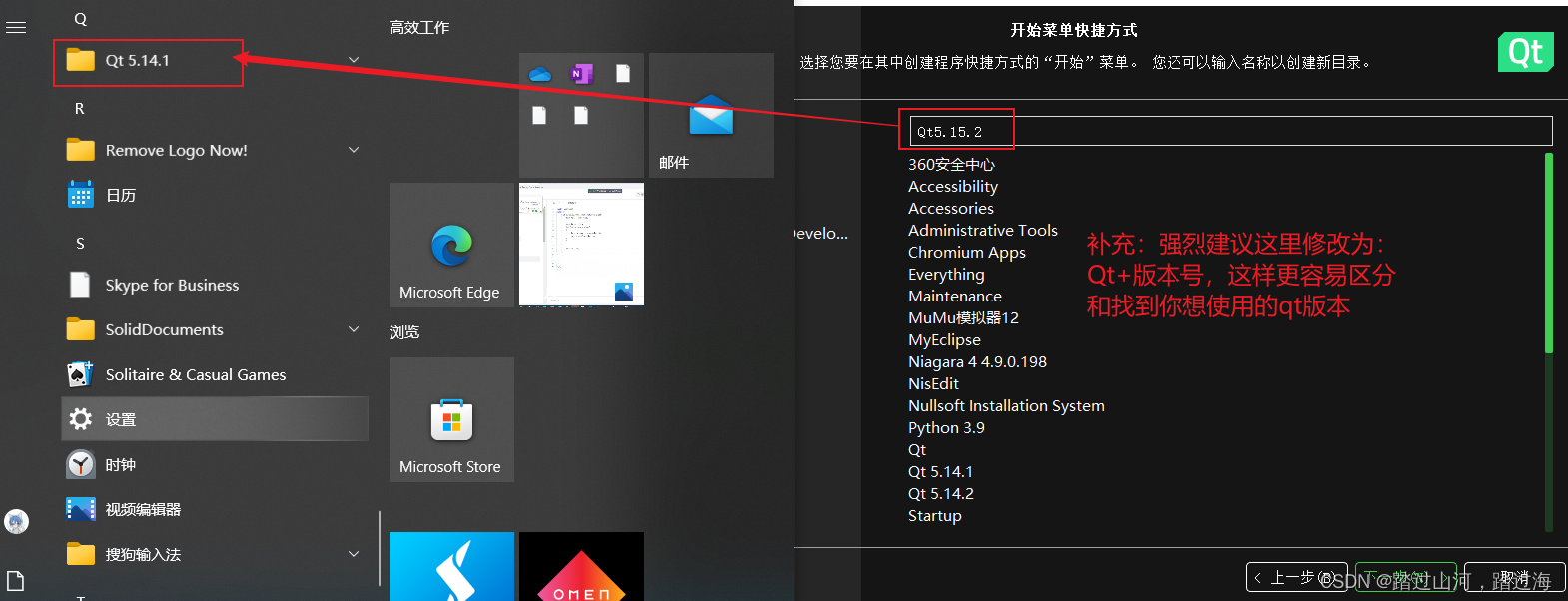
如何判断自己的qt版本呢?
如何判断自己的qt版本呢? 前情提要很简单,按照如下图所示,即可查看当前打开的qtCreator的版本如何打开5.15.2版本的qtCreator呢?安装教程 前情提要 我的电脑已经安装了qt5.14.1,然后我又安装了qt5.15.2,我想尝试一下同一台电脑能否适应两个版本的qt? 当我安装完成qt5.15.2后…...

【文心一言大模型插件制作初体验】制作面试错题本大模型插件
文心一言插件开发初体验 效果图 注意:目前插件仅支持在本地运行,虽然只能自用,但仍然是一个不错的选择。(什么?你说没有用?这不可能!文心一言app可以支持语音,网页端结合手机端就可…...

ROS 2官方文档(基于humble版本)学习笔记(二)
ROS 2官方文档(基于humble版本)学习笔记(二) 理解节点(node)ros2 runros2 node list重映射(remap)ros2 node info 理解话题(topic)rqt_graphros2 topic listr…...

excel中公式结合实际的数据提取出公式计算的分支
要在Excel中使用公式结合实际数据提取分支信息,您可以使用一些文本函数和条件函数来实现这个目标。以下是一个示例,假设您有一个包含银行交易描述的列A,想要从中提取分支信息: 假设交易描述的格式是"分行名称-交易类型"…...

3D模型优化实战:LowPoly、纹理烘焙及格式转换
在快节奏的游戏和虚拟/增强现实 (VR/AR) 世界中,3D 模型的优化在提供引人入胜的体验方面发挥着关键作用。 这门学科不仅仅是创造令人着迷的图形结构; 这是视觉质量和游戏流畅性之间的平衡问题,确保细致而流畅的游戏环境。 通过低多边形建模等…...

genome comparison commend 2 MCMCtree
仅本人练习使用!!后续会逐渐修改!! mcmctree估算物种分歧时间 - 简书 https://www.cnblogs.com/bio-mary/p/12818888.html 估算系统树分歧时间 —— paml.mcmctree,r8s | 生信技工 http://www.chenlianfu.com/?p2948 4. 使用PAM…...

Linux安装JenkinsCLI
项目简介安装目录 mkdir -p /opt/jenkinscli && cd /opt/jenkinscli JenkinsCLI下载 wget http://<your-jenkins-server>/jnlpJars/jenkins-cli.jar # <your-jenkins-server> 替换为你的 Jenkins 服务器地址 JenkinsCLI授权 Dashboard-->Configure Glob…...

Midjourney学习(一)prompt的基础
prompt目录 sd和mj的比较prompt组成风格表现风格时代描述表情色彩情绪环境 sd和mj的比较 自从去年9月份开始,sd就变得非常或火,跟它一起的还有一个midjourney。 他们就像是程序界的两种模式,sd是开源的,有更多的可能性更可控。但是…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
