可能的二分法 -- 二分图判定【DFS、BFS分别实现】
886. 可能的二分法
class PossibleBipartition:"""可能的二分法「其实考察的就是二分图的判定」用dfs和bfs 两种方法分别实现https://leetcode.cn/problems/possible-bipartition/"""def __init__(self):self.success = Trueself.color = []self.visited = []def dfs(self, n, dislikes):"""DFS递归实现:param n: :param dislikes::return:"""# 图节点编号为 1...nself.color = [False] * (n+1)self.visited = [False] * (n+1)graph = self.buildgraph(n, dislikes)# 因为图不一定是联通的,可能存在多个子图# 所以要把每个节点都作为起点进行一次遍历# 如果发现任何一个子图不是二分图,整幅图都不是二分图for v in range(1, n+1):if not self.visited[v]:self.dfs_traverse(graph, v)return self.successdef buildgraph(self, n, dislikes):graph = [[] for _ in range(n+1)]for edge in dislikes:v = edge[1]w = edge[0]# 无向图相当于双向图graph[v].append(w)graph[w].append(v)return graphdef dfs_traverse(self, graph, v):if not self.success:returnself.visited[v] = Truefor w in graph[v]:if not self.visited[w]:self.color[w] = not self.color[v]self.dfs_traverse(graph, w)else:if self.color[v] == self.color[w]:self.success = Falsereturndef bfs(self, n, dislikes):"""BFS实现,用队列替代递归调用:param n::param dislikes::return:"""# 图节点编号为 1...nself.color = [False] * (n + 1)self.visited = [False] * (n + 1)graph = self.buildgraph(n, dislikes)# 因为图不一定是联通的,可能存在多个子图# 所以要把每个节点都作为起点进行一次遍历# 如果发现任何一个子图不是二分图,整幅图都不是二分图for v in range(1, n + 1):if not self.visited[v]:self.bfs_traverse(graph, v)return self.successdef bfs_traverse(self, graph, start):# 节点队列queue = []self.visited[start] = Truequeue.append(start)while queue and self.success:v = queue.pop(0)# 从节点 v 向所有相邻节点扩散for w in graph[v]:if not self.visited[w]:# 相邻节点w没有被访问过# 那么应该给节点w涂上和节点v不同的颜⾊self.color[w] = not self.color[v]# 标记 w 节点,并放⼊队列self.visited[w] = Truequeue.append(w)else:if self.color[v] == self.color[w]:self.success = Falsereturn相关文章:

可能的二分法 -- 二分图判定【DFS、BFS分别实现】
886. 可能的二分法 class PossibleBipartition:"""可能的二分法「其实考察的就是二分图的判定」用dfs和bfs 两种方法分别实现https://leetcode.cn/problems/possible-bipartition/"""def __init__(self):self.success Trueself.color []self.…...

六级翻译备考
classical 经典的 Chinese literature 中国文学 朝代dynasty 统治 rule 社会稳定 steady society 治理有序 orderly governance 伟大的greatest 时代 times或者periods 被人们描绘成人类历史上伴随着治理有序,社会稳定的最伟大的时代之一 more and more越来越多 …...

Vue框架--Vue中的数据绑定
Vue中有两种数据绑定的方式 1.单向数据绑定(v-band):数据只能够从data流向页面 2.双向数据绑定(v-model):数据不仅仅能够从data流向页面,也可以从页面流向data。 备注: 1.双向绑定一般都应用在表单类元素上。(如:input、select等有value属性值的标签上) 2.…...

Unity——热更新浅析
热更新的思想从本质上来讲,要考虑一些问题。例如,一个完整的游戏最多可以有多大比例的资源通过网络加载?能否让尽可能多的资源通过网络加载? 通过网络加载有很多好处,不仅可以极大减小安装包的体积,而且有…...

IMPLEMENT_DYNCREATE的分析
一、介绍 IMPLEMENT_DYNCREATE 是一个宏(macro),通常与DECLARE_DYNCREATE宏一起在MFC框架中使用。它的作用是为一个派生自 CObject 的MFC类提供运行时类型信息(RTTI)和对象的动态创建支持。 具体来说,IMP…...
Java实现根据短连接获取1688商品详情数据,1688淘口令接口,1688API接口封装方法
要通过1688的API获取商品详情数据,您可以使用1688开放平台提供的接口来实现。以下是一种使用Java编程语言实现的示例,展示如何通过1688开放平台API获取商品详情属性数据接口: 首先,确保您已注册成为1688开放平台的开发者…...
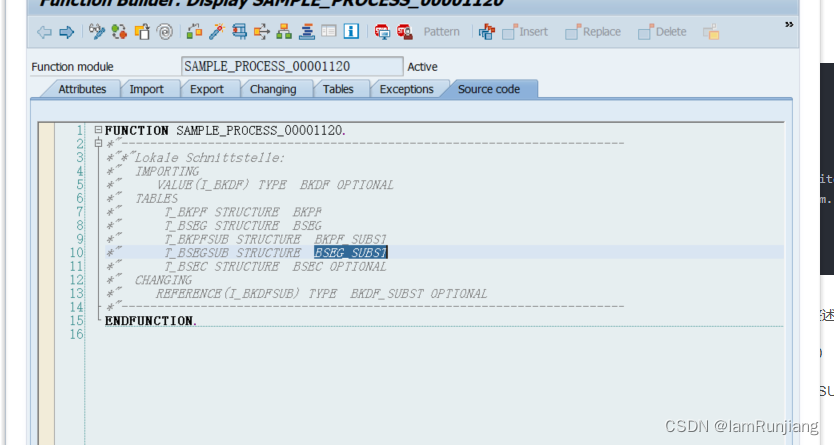
ABAP FICO 凭证替代 凭证校验
凭证校验 1.T-CODE--->GGX2--->GBLR-->ZRGGBR000 2.将程序RGGBR000 复制为ZRGGBR000 3.GGB0--》财务会计--》凭证抬头或者行项目维护检验规则 4.OB28 维护特定的公司代码和调用点和确认,活动等级设置为1 5.GGB4-->激活校验 凭证替代 1.T-CODE--->GG…...

项目验收有哪些流程?
验收流程 科技计划项目验收/课题验收测试服务的被测对象是国家重大专项、科研课题的软件成果物,可以是一个模块、软件或系统等,也可以是软件套件或软件原型等。测试范围主要来源于课题的合同书/可行吧报告/申报书中的技术指标要求。所出具的科技项目验收…...

C++,类的继承
一、继承的基本概念 继承使得C能够从已有的类派生出新的类,而派生类继承了原有类的特征,包括方法。被继承者称为父类或基类,继承者称为子类或派生类。 继承的目的: 实现代码的重用性建立父类和子类之间的联系在实现多态的时候&a…...

作业33333333
一、正向解析 在开启DNS服务之前先将防火墙关闭。 systemctl stop firewalld.service 开启DNS服务,需要开启端先进行安装主软件,以及配置包管理软件 配置包管理软件一般会跟随主软件一起安装,如果没有手动安装一次就可以了。 安装完成之后&…...
Spring Cloud--从零开始搭建微服务基础环境【二】
😀前言 本篇博文是关于Spring Cloud–从零开始搭建微服务基础环境【二】,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以帮助到大家,…...
)
算法工程题(中序遍历)
* 题意说明: * 给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。 * * 示例 1: * 输入:root [1,null,2,3] * 输出:[1,3,2] * * 示例 2: * 输入:root [] * 输出:[] * *…...
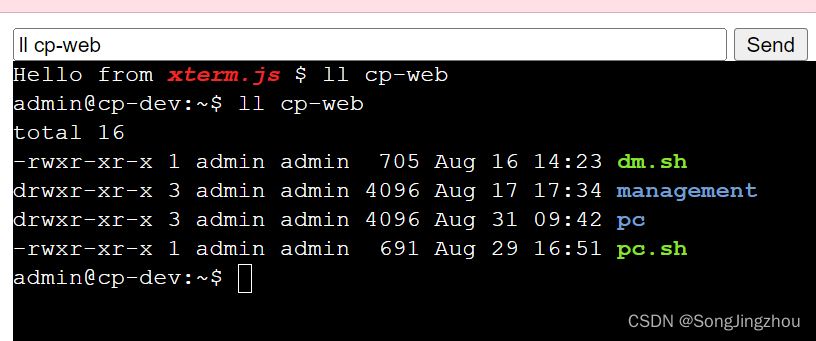
jsch网页版ssh
使用依赖 implementation com.jcraft:jsch:0.1.55Server端代码 import com.jcraft.jsch.Channel; import com.jcraft.jsch.JSch; import com.jcraft.jsch.Session; import java.io.InputStream; import java.io.OutputStream; import java.util.concurrent.TimeUnit; import o…...

教程i.MX8MPlus开发板SPI转CAN操作
飞凌嵌入式OKMX8MP-C核心板有两路原生CAN总线,但用户在开发产品时可能需要用到更多的CAN,这该如何解决呢?今天小编将为大家介绍一种SPI转CAN的方法,供各位工程师小伙伴参考。 说明 OKMX8MP-C核心板有两路原生的SPI总线,…...

Docker中容器的随机命名方式
使用 docker 创建容器时,如果没有用 --name 指定,docker 会为用户选择一个名称, 格式是两个带有下划线的单词,如xxx_yyyy 其相关的实现在此处 pkg/namesgenerator/names-generator.go[1] 源码中有两个数组,第一个是一个…...
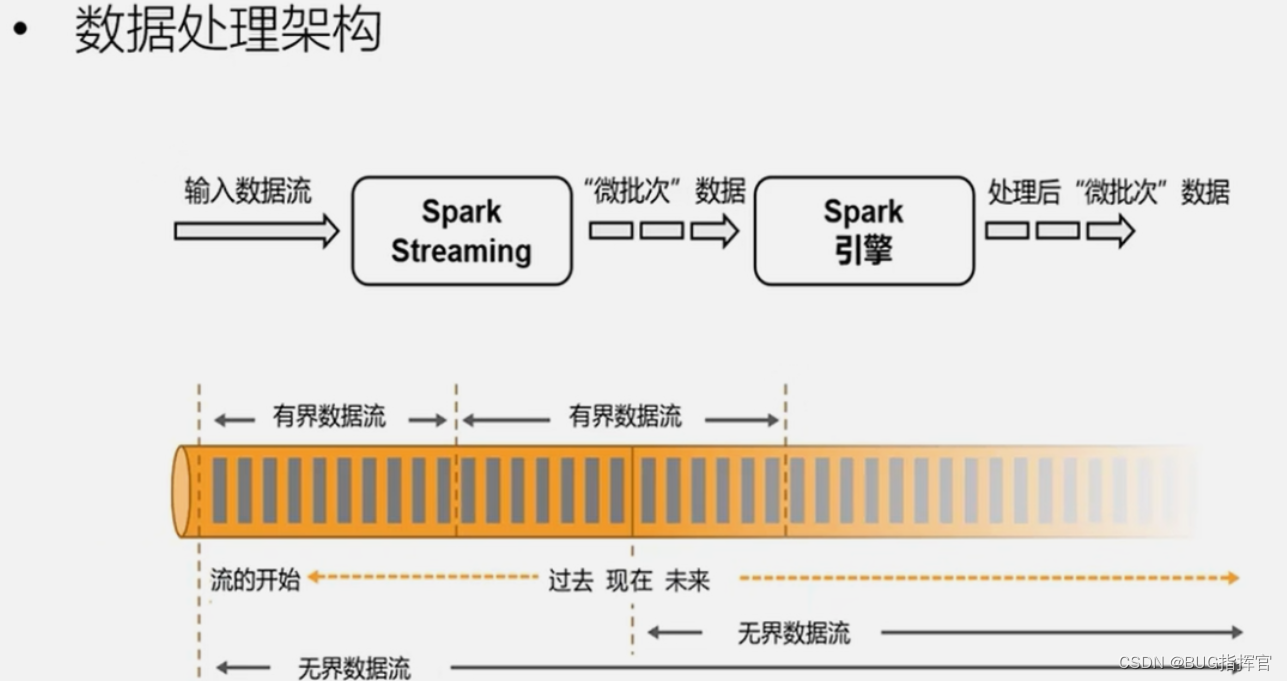
大数据Flink实时计算技术
1、架构 2、应用场景 Flink 功能强大,支持开发和运行多种不同种类的应用程序。它的主要特性包括:批流一体化、精密的状态管理、事件时间支持以及精确一次的状态一致性保障等。在启用高可用选项的情况下,它不存在单点失效问题。事实证明&#…...

数学中的自由与我们的生活
数学中的这些自由可以帮助我们养成很多优秀的品格。具体来说,知识的自由使我们变得足智多谋,让我们可以根据问题的具体情况选择恰当的工具和方法。探索的自由使我们在集体讨论时敢于大声发言,积极提问,让我们在为探索发现而欢呼雀…...

8 python的迭代器和生成器
概述 在上一节,我们介绍了Python的模块和包,包括:什么是模块、导入模块、自定义模块、__name__、什么是包、创建包、导入包等内容。在这一节中,我们将介绍Python的迭代器和生成器。在Python中,迭代器是一个非常重要的概…...
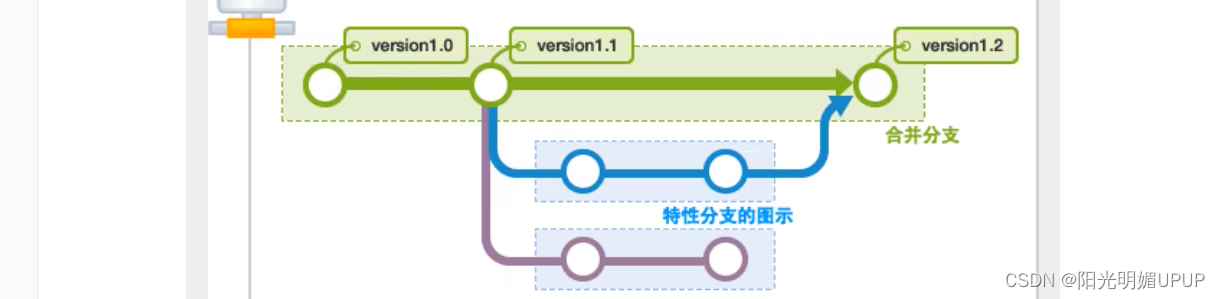
Git的基本使用笔记——狂神说
版本控制 版本迭代, 版本控制( Revision control)是一种在开发的过程中用于管理我们对文件、目录或工程等内容的修改历史,方便查看更改历史记录,备份以便恢复以前的版本的软件工程技术。 实现跨区域多人协同开发 追踪和记载一个或者多个文件的…...

【小程序】外部二维码扫码打开微信小程序并跳转到指定页面
外部二维码扫码打开微信小程序并跳转到指定页面 您需要使用微信提供的跳转链接和相关参数。以下是实现的步骤: 生成跳转链接:使用以下链接格式生成跳转链接,其中APPID是您的小程序的 AppID,PATH是您要跳转的页面路径,…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
