大数据Flink实时计算技术
1、架构
2、应用场景
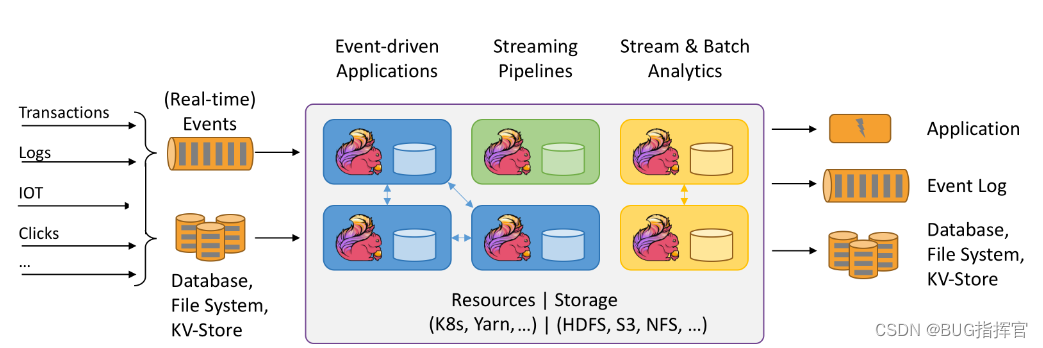
Flink 功能强大,支持开发和运行多种不同种类的应用程序。它的主要特性包括:批流一体化、精密的状态管理、事件时间支持以及精确一次的状态一致性保障等。在启用高可用选项的情况下,它不存在单点失效问题。事实证明,Flink 已经可以扩展到数千核心,其状态可以达到 TB 级别,且仍能保持高吞吐、低延迟的特性。世界各地有很多要求严苛的流处理应用都运行在 Flink 之上。
核心点:
1、高吞吐,低延迟
2、结果的准确性
3、精确一次的状态一致性保证
4、高可用,支持动态扩展

事件驱动型应用
什么是事件驱动型应用?
事件驱动型应用是一类具有状态的应用,它从一个或多个事件流提取数据,并根据到来的事件触发计算、状态更新或其他外部动作。
事件驱动型应用是在计算存储分离的传统应用基础上进化而来。在传统架构中,应用需要读写远程事务型数据库。
相反,事件驱动型应用是基于状态化流处理来完成,数据和计算不会分离,应用只需访问本地(内存或磁盘)即可获取数据。系统容错性的实现依赖于定期向远程持久化存储写入 checkpoint。下图描述了传统应用和事件驱动型应用架构的区别。

事件驱动型应用的优势?
事件驱动型应用无须查询远程数据库,本地数据访问使得它具有更高的吞吐和更低的延迟。而由于定期向远程持久化存储的 checkpoint 工作可以异步、增量式完成,因此对于正常事件处理的影响甚微。事件驱动型应用的优势不仅限于本地数据访问。传统分层架构下,通常多个应用会共享同一个数据库,因而任何对数据库自身的更改(例如:由应用更新或服务扩容导致数据布局发生改变)都需要谨慎协调。反观事件驱动型应用,由于只需考虑自身数据,因此在更改数据表示或服务扩容时所需的协调工作将大大减少。
核心点:
1、定期向远程持久化存储的 checkpoint 可以异步、增量式完成 对正常事件处理影响甚微
2、传统分层架构下,通常多个应用会共享同一个数据库 需考虑数据安全。
3、事件驱动型应用 只需考虑自身数据,在更改数据或服务扩容时所需的协调工作将大大减少
Flink 如何支持事件驱动型应用?
事件驱动型应用会受制于底层流处理系统对时间和状态的把控能力,Flink 诸多优秀特质都是围绕这些方面来设计的。它提供了一系列丰富的状态操作原语,允许以精确一次的一致性语义合并海量规模(TB 级别)的状态数据。此外,Flink 还支持事件时间和自由度极高的定制化窗口逻辑,而且它内置的 ProcessFunction 支持细粒度时间控制,方便实现一些高级业务逻辑。同时,Flink 还拥有一个复杂事件处理(CEP)类库,可以用来检测数据流中的模式。
Flink 中针对事件驱动应用的明星特性当属 savepoint。Savepoint 是一个一致性的状态映像,它可以用来初始化任意状态兼容的应用。在完成一次 savepoint 后,即可放心对应用升级或扩容,还可以启动多个版本的应用来完成 A/B 测试。
核心点:
1、允许以精确一次的一致性语义合并海量规模(TB 级别)的状态数据。
2、支持事件时间和自由度极高的定制化窗口逻辑,内置 ProcessFunction 支持细粒度时间控制。
3、Savepoint 是一个一致性的状态映像,完成一次 savepoint 后,即可放心对应用升级或扩容。
数据分析应用
什么是数据分析应用?
数据分析任务需要从原始数据中提取有价值的信息和指标。传统的分析方式通常是利用批查询,或将事件记录下来并基于此有限数据集构建应用来完成。为了得到最新数据的分析结果,必须先将它们加入分析数据集并重新执行查询或运行应用,随后将结果写入存储系统或生成报告。
借助一些先进的流处理引擎,还可以实时地进行数据分析。和传统模式下读取有限数据集不同,流式查询或应用会接入实时事件流,并随着事件消费持续产生和更新结果。这些结果数据可能会写入外部数据库系统或以内部状态的形式维护。仪表展示应用可以相应地从外部数据库读取数据或直接查询应用的内部状态。
核心点:
1、传统方式通过批处理方式从原始数据提取有用的信息生成报表。
2、流式查询或应用会接入实时事件流,并随着事件消费持续产生和更新结果。
如下图所示,Apache Flink 同时支持流式及批量分析应用。

流式分析应用的优势?
和批量分析相比,由于流式分析省掉了周期性的数据导入和查询过程,因此从事件中获取指标的延迟更低。不仅如此,批量查询必须处理那些由定期导入和输入有界性导致的人工数据边界,而流式查询则无须考虑该问题。
另一方面,流式分析会简化应用抽象。批量查询的流水线通常由多个独立部件组成,需要周期性地调度提取数据和执行查询。如此复杂的流水线操作起来并不容易,一旦某个组件出错将会影响流水线的后续步骤。而流式分析应用整体运行在 Flink 之类的高端流处理系统之上,涵盖了从数据接入到连续结果计算的所有步骤,因此可以依赖底层引擎提供的故障恢复机制。
Flink 如何支持数据分析类应用?
Flink 为持续流式分析和批量分析都提供了良好的支持。具体而言,它内置了一个符合 ANSI 标准的 SQL 接口,将批、流查询的语义统一起来。无论是在记录事件的静态数据集上还是实时事件流上,相同 SQL 查询都会得到一致的结果。同时 Flink 还支持丰富的用户自定义函数,允许在 SQL 中执行定制化代码。如果还需进一步定制逻辑,可以利用 Flink DataStream API 和 DataSet API 进行更低层次的控制。此外,Flink 的 Gelly 库为基于批量数据集的大规模高性能图分析提供了算法和构建模块支持。
数据管道应用
什么是数据管道?
提取-转换-加载(ETL)是一种在存储系统之间进行数据转换和迁移的常用方法。ETL 作业通常会周期性地触发,将数据从事务型数据库拷贝到分析型数据库或数据仓库。
数据管道和 ETL 作业的用途相似,都可以转换、丰富数据,并将其从某个存储系统移动到另一个。但数据管道是以持续流模式运行,而非周期性触发。因此它支持从一个不断生成数据的源头读取记录,并将它们以低延迟移动到终点。例如:数据管道可以用来监控文件系统目录中的新文件,并将其数据写入事件日志;另一个应用可能会将事件流物化到数据库或增量构建和优化查询索引。
下图描述了周期性 ETL 作业和持续数据管道的差异。
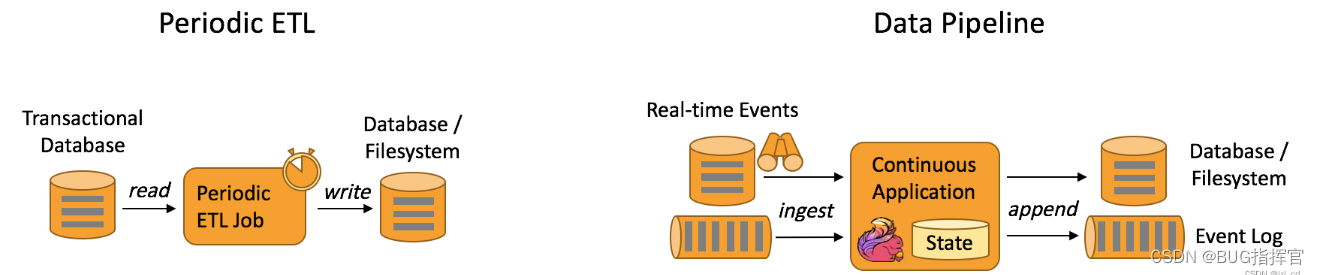
数据管道的优势?
和周期性 ETL 作业相比,持续数据管道可以明显降低将数据移动到目的端的延迟。此外,由于它能够持续消费和发送数据,因此用途更广,支持用例更多。
Flink 如何支持数据管道应用?
很多常见的数据转换和增强操作可以利用 Flink 的 SQL 接口(或 Table API)及用户自定义函数解决。如果数据管道有更高级的需求,可以选择更通用的 DataStream API 来实现。Flink 为多种数据存储系统(如:Kafka、Kinesis、Elasticsearch、JDBC数据库系统等)内置了连接器。同时它还提供了文件系统的连续型数据源及数据汇,可用来监控目录变化和以时间分区的方式写入文件。
分层 API
Flink 根据抽象程度分层,提供了三种不同的 API。每一种 API 在简洁性和表达力上有着不同的侧重,并且针对不同的应用场景。
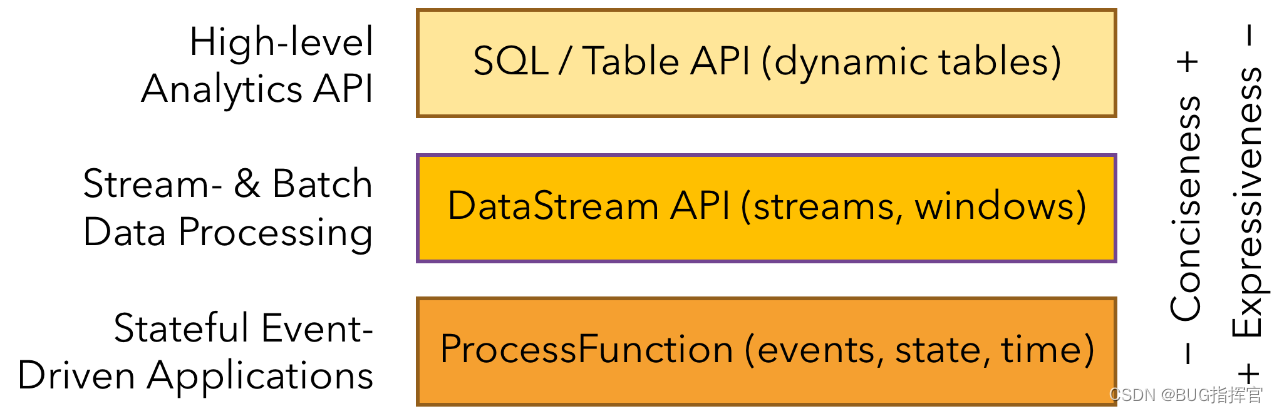
1、越顶层的抽象,表达含义越简明,使用越方便 。
2、越底层越具体,表达能力越丰富,使用越灵活。
Flink VS Spark
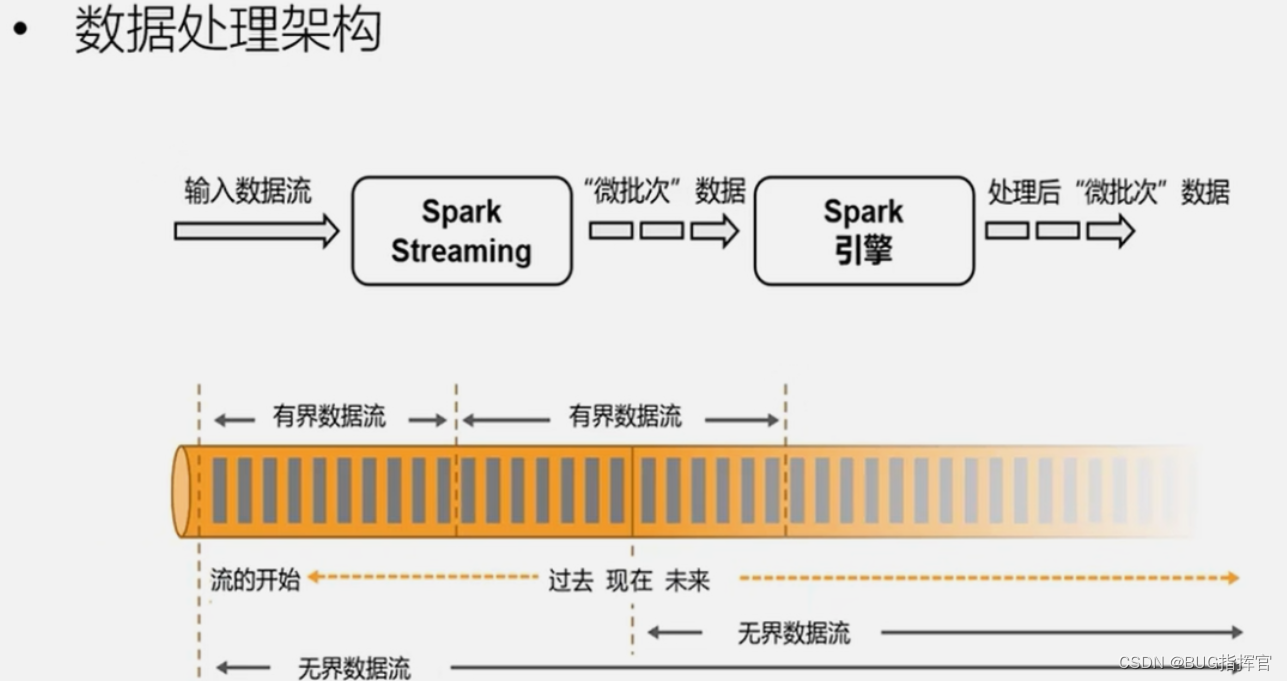
数据模型
spark 采用 RDD 模型,Spark Streaming 的 DStream 实际上也就是一组组小批数据RDD的集合。
flink 的基本数据模型是数据流以及时间序列。
运行时架构
spark是批计算,将DAG划分为不同的Stage,一个完成后才可以计算下一个。
flink是标准的流执行模式,一个事件在一个节点处理完后可以直接发往下一个节点进行处理。
相关文章:

大数据Flink实时计算技术
1、架构 2、应用场景 Flink 功能强大,支持开发和运行多种不同种类的应用程序。它的主要特性包括:批流一体化、精密的状态管理、事件时间支持以及精确一次的状态一致性保障等。在启用高可用选项的情况下,它不存在单点失效问题。事实证明&#…...

数学中的自由与我们的生活
数学中的这些自由可以帮助我们养成很多优秀的品格。具体来说,知识的自由使我们变得足智多谋,让我们可以根据问题的具体情况选择恰当的工具和方法。探索的自由使我们在集体讨论时敢于大声发言,积极提问,让我们在为探索发现而欢呼雀…...

8 python的迭代器和生成器
概述 在上一节,我们介绍了Python的模块和包,包括:什么是模块、导入模块、自定义模块、__name__、什么是包、创建包、导入包等内容。在这一节中,我们将介绍Python的迭代器和生成器。在Python中,迭代器是一个非常重要的概…...
Git的基本使用笔记——狂神说
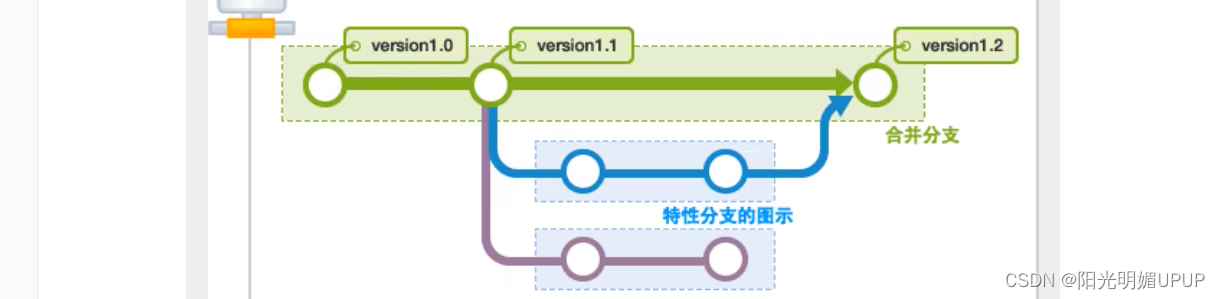
版本控制 版本迭代, 版本控制( Revision control)是一种在开发的过程中用于管理我们对文件、目录或工程等内容的修改历史,方便查看更改历史记录,备份以便恢复以前的版本的软件工程技术。 实现跨区域多人协同开发 追踪和记载一个或者多个文件的…...

【小程序】外部二维码扫码打开微信小程序并跳转到指定页面
外部二维码扫码打开微信小程序并跳转到指定页面 您需要使用微信提供的跳转链接和相关参数。以下是实现的步骤: 生成跳转链接:使用以下链接格式生成跳转链接,其中APPID是您的小程序的 AppID,PATH是您要跳转的页面路径,…...

bazel安装
安装 首先安装一下 Bazel 环境。参考 https://bazel.build/install。我是在 Ubuntu 上实验的,所以安装过程参考的是:https://bazel.build/install/ubuntu,有很多种安装方法,我选择的是使用二进制安装程序。这个具体参考的又是 ht…...

Typescript的class语法[类]的操作和应用
TypeScript 是一种面向对象的编程语言,它扩展了 JavaScript,为其添加了类型系统和其他一些特性。TypeScript 的 class 语法可以让开发者更加方便地使用面向对象的编程方式。本文将详细介绍 TypeScript 的 class 语法的操作和应用,并提供代码案…...

OPENCV实现暴力特征匹配
# -*- coding:utf-8 -*- """ 作者:794919561 日期:2023/9/1 """ import cv2 import numpy as np# 读...

揭秘亚马逊Amazon测评,掌握细节和技巧,提升产品销量和评论数量
亚马逊是全球最大的跨境电商平台,拥有全球65个国家的几十个网站。对于跨境卖家来说,亚马逊是最值得选择的平台之一。 亚马逊的八大站点分别是美国、加拿大、墨西哥、欧洲、澳大利亚、日本、中东和巴西。 美国站点是全球最大的零售市场,拥有…...
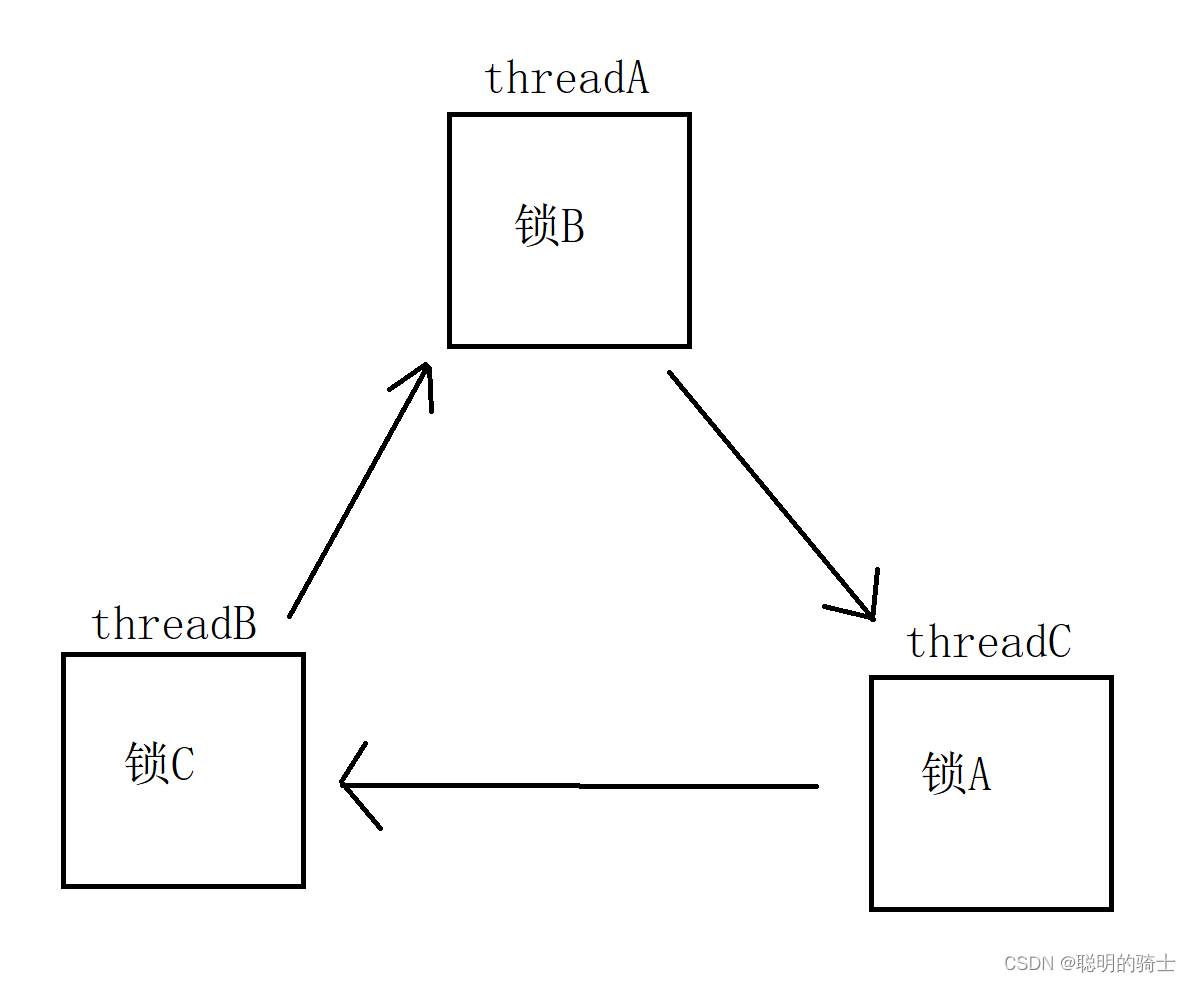
Linux线程互斥
目录 一、线程不安全 1.线程不安全现象 2.线程不安全程序的特质 3.线程不安全程序的原因 二、线程互斥 1.基本概念 2.锁 (1)认识锁 (2)互斥锁的使用 (3)代码的改造 3.锁的本质 (1&a…...

【仿写spring之ioc篇】三、检查是否实现了Aware接口并且执行对应的方法
Aware接口 Aware接口中只是设置了对应的set方法,目前只定义了三个Aware 以BeanNameAware为例 package com.ez4sterben.spring.ioc.factory.aware;/*** bean名字清楚** author ez4sterben* date 2023/08/31*/ public interface BeanNameAware {/*** 设置beanName* …...
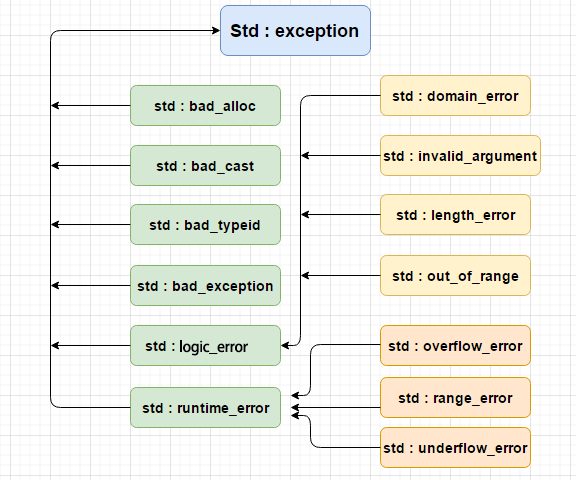
C++ 异常处理
C 异常(Exception)是指在程序运行时产生的特殊情况,例如,尝试除以零的操作。异常提供了一种转移程序控制权的方式,异常处理涉及到三个关键字:try、catch、throw。 throw: 当问题出现时,程序会抛出一个异常。这是通过…...

OJ练习第157题——单词拆分
单词拆分 力扣链接:139. 单词拆分 题目描述 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 示例 …...
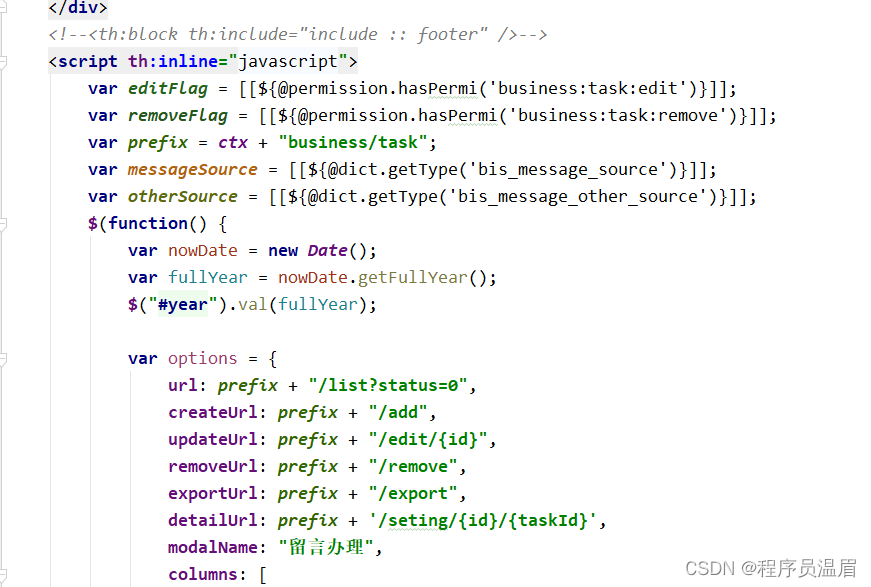
若依tab-content面板失效、使用load的解决方法(附详细步骤)
【版权所有,文章允许转载,但须以链接方式注明源地址,否则追究法律责任】【创作不易,点个赞就是对我最大的支持】 前言 仅作为学习笔记,供大家参考 总结的不错的话,记得点赞收藏关注哦! 思路&…...

2023年03月 C/C++(五级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:拼点游戏 C和S两位同学一起玩拼点游戏。有一堆白色卡牌和一堆蓝色卡牌,每张卡牌上写了一个整数点数。C随机抽取n张白色卡牌,S随机抽取n张蓝色卡牌,他们进行n回合拼点,每次两人各出一张卡牌,点数大者获…...
Android安卓实战项目(12)—关于身体分析,BMI计算,喝水提醒,食物卡路里计算APP【支持中英文切换】生活助手类APP(源码在文末)
Android安卓实战项目(12)—关于身体分析,BMI计算,喝水提醒,食物卡路里计算APP【支持中英文切换】生活助手类APP(源码在文末🐕🐕🐕) 一.项目运行介绍 B站演示…...

Hadoop 3.2.4 集群搭建详细图文教程
目录 一、集群简介 二、Hadoop 集群部署方式 三、集群安装 3.1 集群角色规划 3.2 服务器基础环境准备 3.2.1 环境初始化 3.2.2 ssh 免密登录(在 hadoop01 上执行) 3.2.3 各个节点上安装 JDK 1.8 环境 3.3 安装 Hadoop 3.4 Hadoop 安装包目…...

STL的学习之一
1)STL扫盲 1)C标准库和标准模板库是不一样的 2)标准模板库是用泛型编程方式编写的函数或者类库; 3) SGI STL linux一般用,P.J.Plauger STL,visual2017 windows用 STL六大组件 : 容器,迭代器 STL 算法(说白了就是函数…...

如何使用Python进行数据科学实验?
使用Python进行数据科学实验通常需要以下步骤: 以上仅为使用Python进行数据科学实验的基本步骤,具体实验过程会根据具体问题和数据集的特点而有所不同。可以进一步学习和探索相关的数据科学和机器学习技术,以提高实验的效果和表现。 安装Pyt…...

华为数通方向HCIP-DataCom H12-821题库(拖拽题,知识点总结)
以下是我在现有题库中整理的需要重点关注的考点内容,如有遗漏小伙伴可以留言补充。...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...