动态规划之连续乘积最大子数组 连续和最大子数组
一. 连续和最大子数组
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:输入:nums = [1]
输出:1
示例 3:输入:nums = [5,4,-1,7,8]
输出:23
1.1 怎么想到使用动态规划?
当然是题目给的建议。
- 题目中讲,求最大和。
- 题目中讲,返回最大和。
我们要做的是求一个目标值(通常最大,最小), 不要求过程,只要结果。 对于这种题目,我们通常使用动态规划。
1.2 动态规划第一步该做什么?
首先明确几个关键点。
- 最大连续子数组,与子序列区别开,即数组下标连续。
- 和最大,针对每个【i】怎么计算子问题。
当然就是找到状态转移方程啊!
f ( i ) = { f ( i − 1 ) + i ( i < = f ( i − 1 ) + i ) i ( i > f ( i − 1 ) + i ) f(i) =\left\{ \begin{aligned} f(i-1) + i (i <= f(i-1) + i) \\ i (i > f(i-1) + i) \end{aligned} \right. f(i)={f(i−1)+i(i<=f(i−1)+i)i(i>f(i−1)+i)
求和的状态转移方程很简单。当我们有了 i - 1位置的结果,去求 i位置的连续子数组和,当然就是用 f ( i − 1 ) + i 和 i f(i-1) + i 和 i f(i−1)+i和i 比较一下,拿最大的呀
仔细想想,这不对吧?
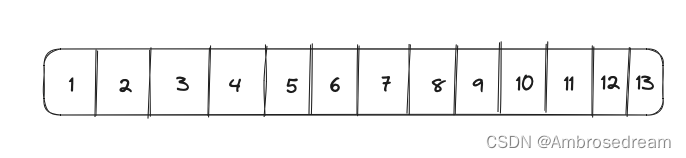
这有什么不对的呢?
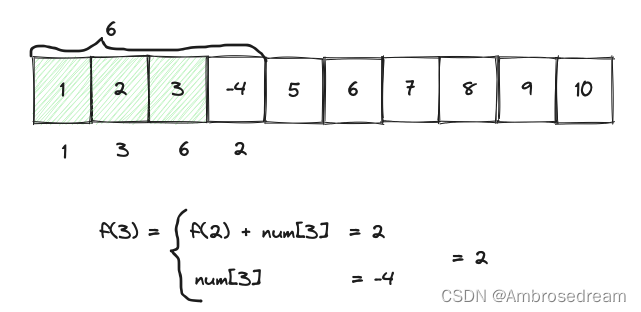
明显,前4个最大连续和是 1 + 2 + 3 = 6。
所以错在哪里了呢?或者说,我们怎么计算能得到6呢?
…
很简单,return 2 > 6 ? 2 : 6 不就行了吗
我们的函数计算的值是以当前坐标为结尾的数组的最大子数组。
动态规划的子问题和整体问题求的目标是一致的,只有状态再更迭,此处的状态就是下标index。
计算得到函数要与旧的最大值进行比较取最大。
fun maxSubArray(nums []int) int {pre, res := 0, nums[0]for _, v := range nums {pre = max(pre + v, v)res = max(res, pre)}return res
}
二. 连续乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
2.1 这个题目使用什么方法?
- 乘积最大。
- 返回乘积。
- 连续子数组。
这俩题目,是不是一样的。先想一想差别。
求最大值,返回结果, 那使用动态规划没什么问题。
2.2 直接写代码
fun maxSubArray(nums []int) int {pre, res := 1, nums[0]for _, v := range nums {pre = max(pre * v, v)res = max(res, pre)}return res
}
因为乘法,所以pre初始值改为1 。
会有问题吗?
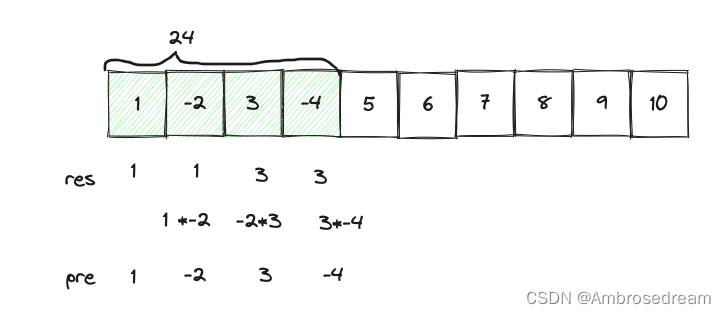
明显的错误…
只是加法变乘法,原来的方案就行不通了。
问题就在于,乘法遇到负数,从最大变成了最小,-4 * 3 = -12
所以我们需要对这个负号进行一下特殊的处理。
2.3 状态该怎么变化呢?
如果遇到负数,我们希望使用一个最小的值与其做乘积运算,期望得到一个最大的值; 反之遇到正数,我们要用一个最大的值进行乘积运算。
所以,我们需要记两个值,分别是一个最大的preMax 和一个最小的preMin.
p r e M a x = f ( i ) m a x p r e M i n = f ( i ) m i n p r e M a x = M a x ( f ( i − 1 ) m a x ∗ n u m [ i ] , f ( i − 1 ) m i n ∗ n u m [ i ] , n u m [ I ] ) p r e M i n = M i n ( f ( i − 1 ) m i n ∗ n u m [ i ] , f ( i − 1 ) m a x ∗ n u m [ i ] , n u m [ I ] ) preMax = f(i)_{max} \\ preMin = f(i)_{min}\\ preMax = Max(f(i-1)_{max}*num[i], f(i-1)_{min} * num[i], num[I])\\ preMin= Min(f(i-1)_{min}*num[i], f(i-1)_{max} * num[i], num[I]) preMax=f(i)maxpreMin=f(i)minpreMax=Max(f(i−1)max∗num[i],f(i−1)min∗num[i],num[I])preMin=Min(f(i−1)min∗num[i],f(i−1)max∗num[i],num[I])
代码就比较简单了
func maxProduct(nums []int) int {preMax,preMin, res := 1,1, nums[0]for _,v := range nums {mn,mx := preMin,preMaxpreMax = max(mx * v, max(mn * v,v))preMin = min(mn * v, min(mx * v,v))res = max(preMax,res)}return res
为什么多了一行mn,mx := preMin,preMax
你可以去掉试试看~
20230902记录,今天先到这里。
相关文章:

动态规划之连续乘积最大子数组 连续和最大子数组
一. 连续和最大子数组 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入:nums [-2,1,-3,4,-1,2,1,-5,…...

keil在点击debug无法运行(全速运行)
1、今天发现我之前可以debug的程序,在板子上无法debug了,打断点完全没用 2、换了电脑,带板子过去也这样,之前可以运行的代码都debug不了 3、按照网上的方法,都不行,全速运行,单步执行都是灰色…...

go语言-协程
mOS结构体 每一种操作系统不同的线程信息 g给g0栈给g0协程内存中分配的地址,记录函数跳转信息, 单线程循环 0.x版本 1.0版本 多线程循环 操作系统并不知道Goroutine的存在 操作系统线程执行一个调度循环,顺序执行Goroutine 调度循环非常…...

如何伪造http头,让后端认为是本地访问
0x00 前言 这个知识点纯粹就是为了ctf准备的,很少有系统会出现这种情况。 0x01 正文 1.host头 如果后端从host取值来判断是否是本地就可以通过此方法进行绕过: host: 127.0.0.12.X-Forwarded-For X-Forwarded-For(XFF)是用来…...
视频剪辑音效处理软件有哪些?视频剪辑软件那个好用
音效是视频剪辑的重要部分,能起到画龙点睛的作用。在短视频平台中,一段出彩的音效能将原本平平无奇的视频变得生动有趣。那么,视频剪辑音效处理软件有哪些?本文会给大家介绍好用的音效处理软件,同时也会介绍视频剪辑音…...

搭建STM32F407的Freertos系统(基于STM32CubeMX)
本人长期开发Linux、Windows上应用软件,一直以来MCU开发有所接触,但较少(最近项目需要,小公司么,都得会,被逼的),好在有STM32CubeMX这样工具,貌似就是我想要的工具。 本次…...
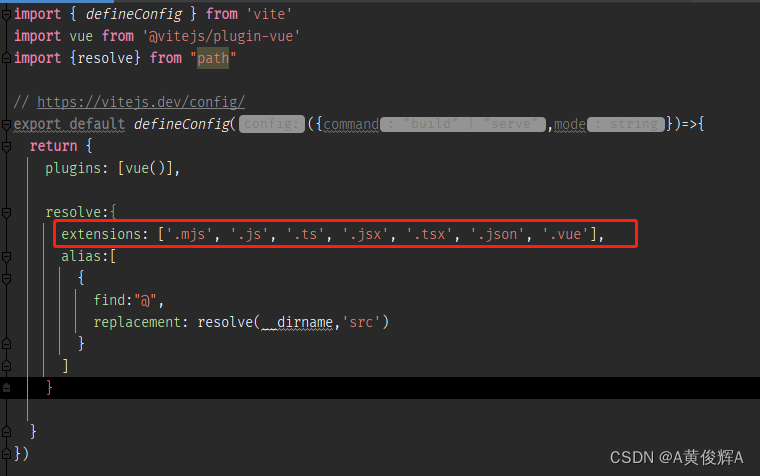
vite 配置自动补全文件的后缀名
vite 不建议自动补全,文件的后缀名的 const Home ()>import("/views/Home.vue");文件是必须要加上 .vue 的后缀名的 如果 想要像 webpack 一样的不用写, 可以在vite.config.js中配置如下就可以了...

基于Spring Boot的人才公寓管理系统设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的人才公寓管理系统设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java spring…...

Python 编写函数
文章目录 条件语句循环语句自定义函数函数参数的传递类型函数的参数传入方法 lambda, map, filter, reduce 函数try-except 语句调试一些常用的内置函数 条件语句 编写程序时,经常用到一些条件或判断,需要用到 if 语句,它的字面意思是&#…...
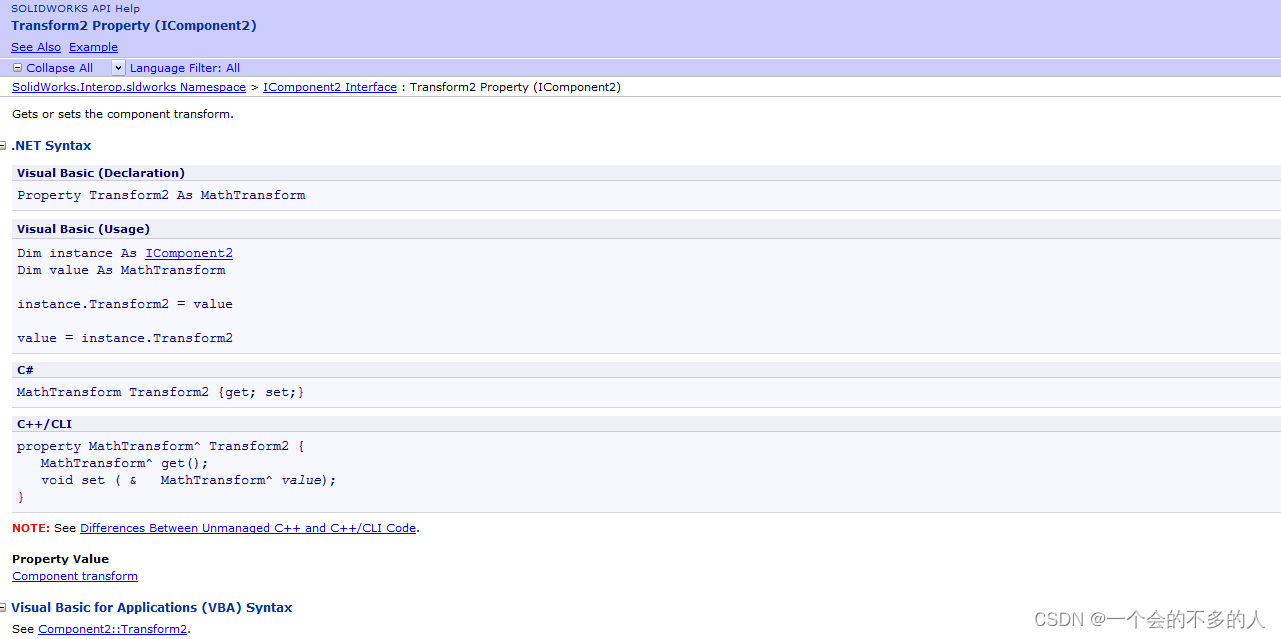
C# Solidworks二次开发:创建距离配合以及移动组件API详解
今天要讲的文章是关于如何创建距离配合和移动组件的API详解。 (1)创建配合API,CreateMate() 这个API的解释是根据指定的特性数据对象来创建配合,也就可以理解为输入什么样的特征对象就可以创建出什么配合,这个API的输…...
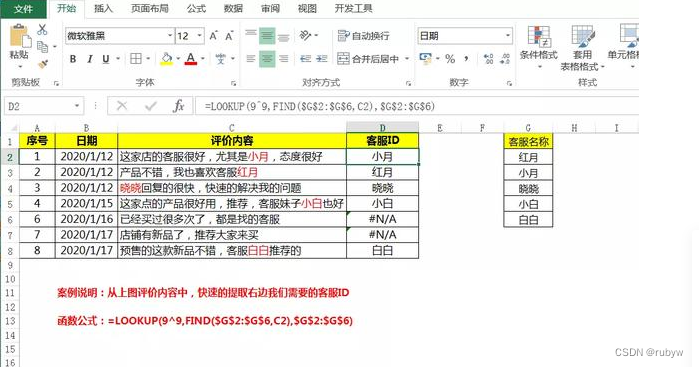
Excel:通过Lookup函数提取指定文本关键词
函数公式:LOOKUP(9^9,FIND($G 2 : 2: 2:G 6 , C 2 ) , 6,C2), 6,C2),G 2 : 2: 2:G$6) 公式解释: lookup第一参数为9^9:代表的是一个极大值的数据,查询位置里面最接近这一个值的数据;lookup第二参数用find函数代替&am…...
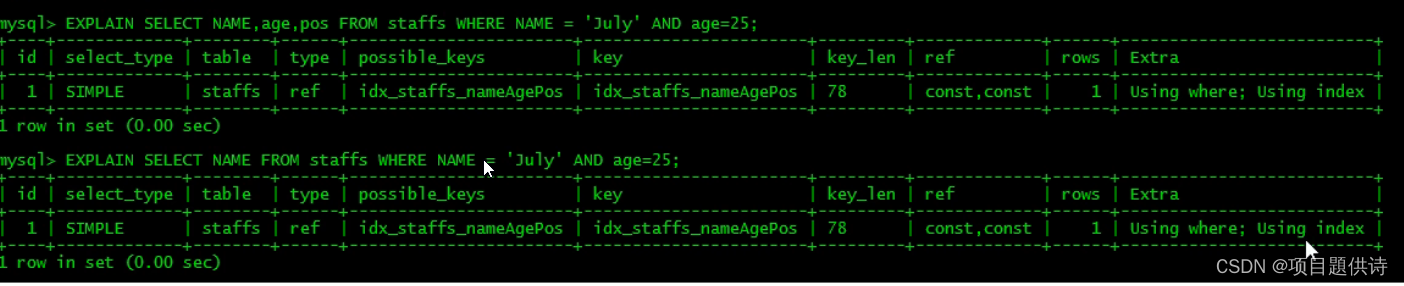
sql:SQL优化知识点记录(六)
(1)索引优化1 查看一下有没有建立索引: 用到索引中的一个:type中的ref决定访问性能 用到索引中的两个:通过key_len的长度可以看出来,比第一个大一点。或者通过ref:中用到了两个常量const 用到了…...
C#搭建WebSocket服务实现通讯
在学习使用websocket之前我们先了解一下websocket: WebSocket是一种在单个TCP连接上进行全双工通信的通信协议。与HTTP协议不同,它允许服务器主动向客户端发送数据,而不需要客户端明确地请求。这使得WebSocket非常适合需要实时或持续通信的应…...
eclipse/STS(Spring Tool Suite)安装CDT环境(C/C++)
在线安装 help -> eclipse marketplace 可以发现,我所使用eclipse给我推荐安装的CDT是10.5版本 离线安装 下载离线安装包 下载地址:https://github.com/eclipse-cdt/cdt/blob/main/Downloads.md 可以看到利息安装包主要有如下四大类,…...

Python爬虫抓取经过JS加密的API数据的实现步骤
随着互联网的快速发展,越来越多的网站和应用程序提供了API接口,方便开发者获取数据。然而,为了保护数据的安全性和防止漏洞,一些API接口采用了JS加密技术这种加密技术使得数据在传输过程中更加安全,但也给爬虫开发带来…...
Nacos基础(2)——nacos的服务器和命名空间 springBoot整合nacos 多个nacos配置的情况
目录 引出nacos服务器和命名空间Nacos服务器命名空间 springBoot整合nacosspringcloud Alibaba 版本与springcloud对应关系引包配置maincontroller 报错以及解决【报错】错误:缺少服务名称报错:9848端口未开放 启动测试引入多个nacos配置多个配置的情况没…...

Win7设备和打印机里空白,0个对象,但是可以打印的处理办法
呉師傅 你是不是遇到过Win7系统打开设备和打印机的时候显示是空白的,0个设备的情况?要怎么操作才能解决这一问题呢,下面就分享一下如何处理这个问题的小方法大家可以尝试一下。 问题如下: 解决方法: 1、点击桌面左下…...

Python基础学习第六天:Python 数据类型
内置数据类型 在编程中,数据类型是一个重要的概念。 变量可以存储不同类型的数据,并且不同类型可以执行不同的操作。 在这些类别中,Python 默认拥有以下内置数据类型: 获取数据类型 您可以使用 type() 函数获取任何对象的数据…...
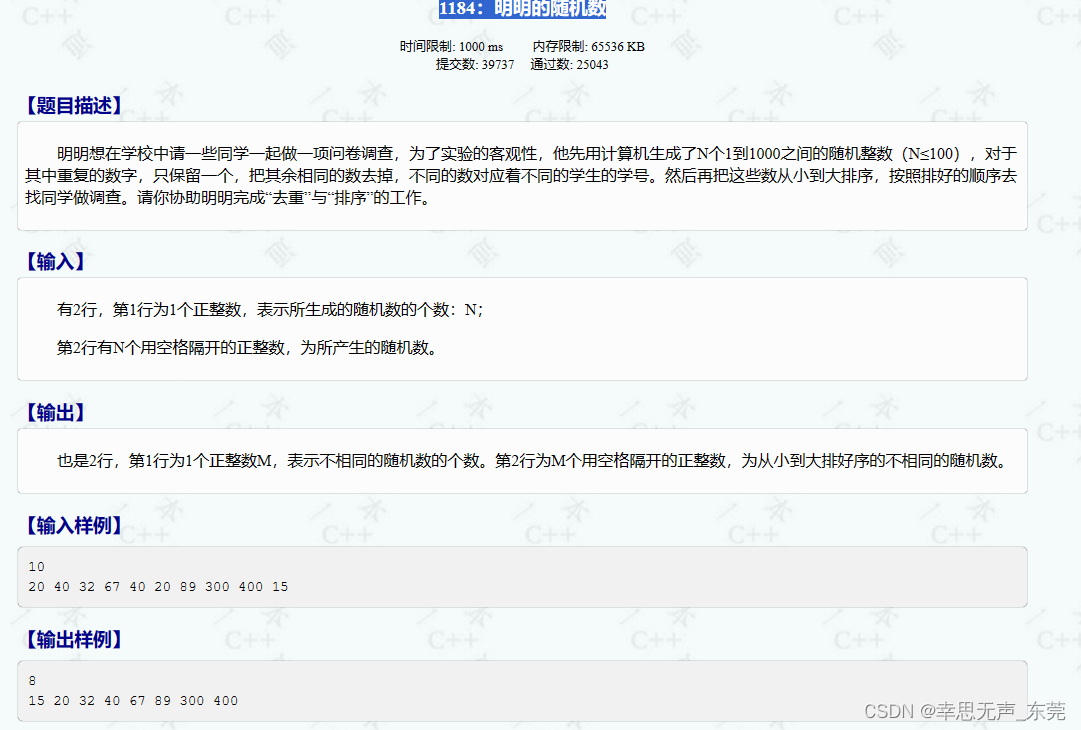
C++信息学奥赛1184:明明的随机数
#include <bits/stdc.h> using namespace std; int main() {int n; // 数组长度cin >> n; // 输入数组长度int arr[n]; // 定义整数数组,用于存储输入的整数// 输入数组元素for (int i 0; i < n; i){cin >> arr[i];}int e 0; // 计数器&…...
NoSQL技术——Redis
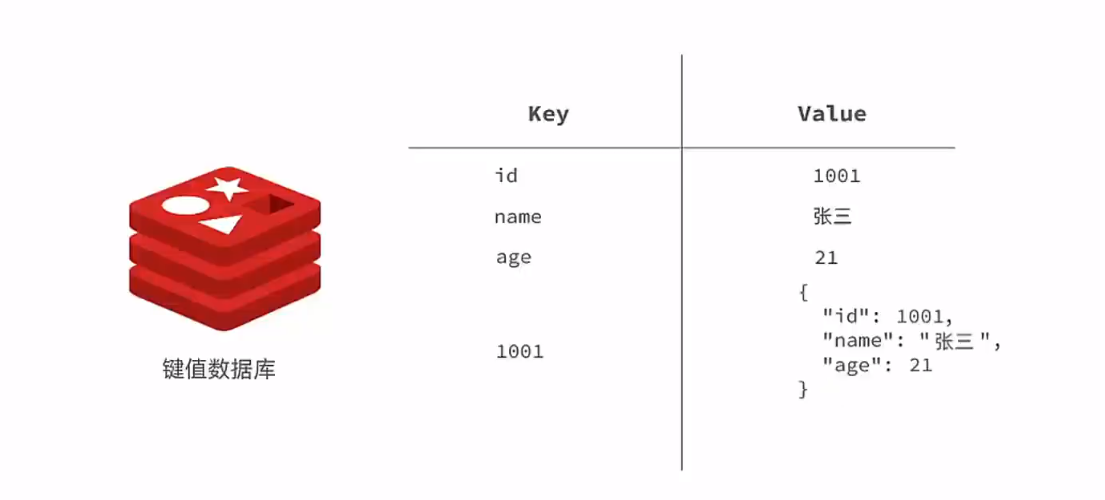
简单介绍 Redis是当下最流行的NoSQL数据库。在Redis中,数据的存储格式是以键值对的方式进行存储的。在键值对的存储形式中,值除了是常见的字符串,也可以是类似于Json对象的形式,或者是List,Map等数组格式,…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
