Leetcode---360周赛
题目列表
2833. 距离原点最远的点
2834. 找出美丽数组的最小和
2835. 使子序列的和等于目标的最少操作次数
2836. 在传球游戏中最大化函数值
一、距离原点最远的点

这题主要是理解题意,遇到'L'往左走,遇到'R'往右走,遇到'_'左右都可以走,题目问移动完成后,距离原点的最长距离,这很显然,只有所有的‘_’都往一个方向走的时候,才是最大的
代码如下
class Solution {
public:int furthestDistanceFromOrigin(string moves) {int ret=0,l=0;for(int i=0;i<moves.size();i++){if(moves[i]=='L') l++;else if(moves[i]=='R') l--;else ret++;}ret+=abs(l);return ret;}
};二、找出美丽数组的最小和
这题和359周赛的第二题一样,就不再写了,贴个代码
class Solution {
public:long long minimumPossibleSum(int n, int target) {long long m=min(target/2,n);return m*(m+1)/2+(target+target+(n-m-1))*(n-m)/2;}
};三、使子序列的和等于目标的最小操作次数
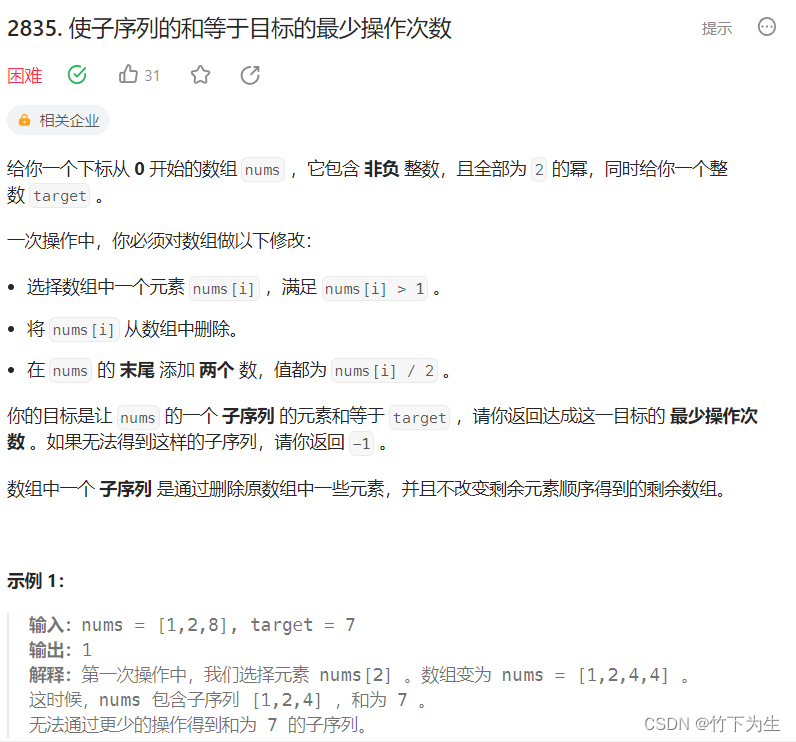
这题思路在于,题目给的数组存放的是2的幂,我们要想到数的二进制表示,从而想到用nums中的数据来凑出target的每一个二进制位上的1。
而target的每一个二进制上的1,有三个来源:
1.数组本身就有
2.用<2^i的数凑出一个2^i
3.将大于2^i的数拆分成我们需要的2^i
而题目要求我们返回最少的操作次数,那么我们肯定优先前两个方案,尽量避免拆分,所以我们将nums数组排序,并且从低位开始枚举target的二进制位上的1
方案一和方案二可以合并成:用<=2^i的数字凑出2^i
首先我们明确<=2^i的各个数字之和一定>=2^i才有可能凑出2^i,接下来,我们用数学归纳法进行证明用<=2^i的数子之和>=2^i的这些数一定能凑出2^i,s代表<=2^i的数字之和
当i=1,s>=2时,用<=2的数凑出2
1)如果存在2,很显然直接得到2
2)如果不存在2,那么<2^1的数字只能是1,而1相加很显然能得到2^1
所以,<=2^1的数字之和>=2^1的这些数一定能凑出2^1
当i=2,s>=4时,用<=4的数凑出4
1)如果存在4,显然能得到4
2)如果不存在4,<4的数字只能是1/2,即<=2^1,且s>=4>=2,所以根据上面的结论,得到一个2,剩下s-2>=2,同理,还能得到一个2,两个2相加得到4
所以,<=2^2的数字之和>=2^2的这些数一定能凑出2^2
当i=3,s>=8时,用<=8的数凑出8
1)如果存在8,显然能得到8
2)如果不存在8,<8的数字只能是1/2/4,即<=2^2,且s>=8>=4,所以根据上面的结论,得到一个4,剩下s-4>=4,同理,还能得到一个4,两个4相加得到8
所以,<=2^3的数字之和>=2^3的这些数一定能凑出2^3
综上所诉,一直这样推到下去就会得到:用<=2^i的数子之和>=2^i的这些数一定能凑出2^i
方案三:根据题目要求,我们选择数组中离2^i最近的2^j (j>i) 进行拆分,这样操作次数最少,而我们很容易知道,一旦差分了2^j,那么2^(i+1),2^(i+2),...,2^(j-1)就都不用考虑了,因为在拆分2^j时,已经得到了这些数,拆分的次数为 j-i (可以找个例子看看)
那么这题什么时候返回-1,我们知道任何一个2的幂都能被拆成1,所以只有数组之和小于target时,才会返回-1
技巧:当我们在凑出2^i之后,原本的算法应该是需要减去2^i,再去看剩下的数能不能凑出下一个2^i,但是我们也可以只加不减,只要我们在比较时,连同target的二进制i位之前的位数一起比较
代码如下
class Solution {
public:int minOperations(vector<int>& nums, int target) {//返回-1的情况if(accumulate(nums.begin(),nums.end(),0LL)<target)return -1;//记录每一位二级制1的个数long long cnt[32]={0};for(auto&x:nums)cnt[__builtin_ctz(x)]++;//__builtin_ctz得到最右边二进制位1的位数int i=0,ret=0;long long sum=0;while(target>=(1u<<i)){sum+=cnt[i]<<i;int mask=(1u<<(i+1))-1;//小技巧if(sum>=(mask&target)){//能凑出来i++;continue;}//需要拆分i++,ret++;while(cnt[i]==0)i++,ret++;}return ret;}
};四、在传球游戏中最大化函数值
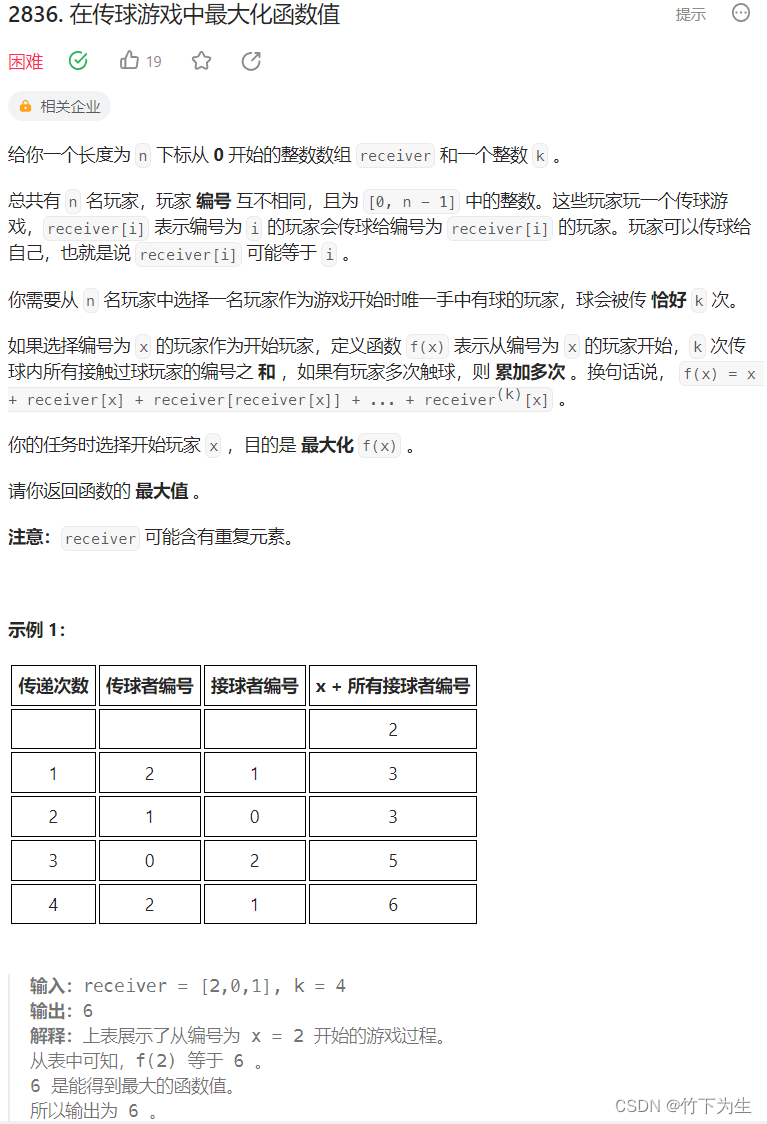
这题题目看起来很复杂,但是其实就是让你求传k次球之后得到的最大下标和,如果直接暴力,这题的数据范围肯定会超时,所以这题就是让我们优化时间复杂度,
这里要提到一个倍增的算法思想,本质就是预处理记录每个球员传2^i次球后的得分和接到球的人的下标(这里用x^i都无所谓,只是2^i比较好计算),根据数据范围可以知道,这样每个人的求解时间都在O(logk)以内,时间复杂度为O(nlogk)
代码如下
class Solution {
public:long long getMaxFunctionValue(vector<int>& receiver, long long k) {int n=receiver.size();int m=64 - __builtin_clzll(k);//k的二进制长度int g[n][m+1];//记录2^i后的接球人的下标long long f[n][m+1];//记录2^i后得到的下标和for(int i=0;i<n;i++)//初始化f[i][0]=g[i][0]=receiver[i];//预处理for(int i=1;i<m+1;i++){for(int j=0;j<n;j++){g[j][i]=g[g[j][i-1]][i-1];f[j][i]=f[j][i-1]+f[g[j][i-1]][i-1];}}long long ans=0;for(int i=0;i<n;i++){long long res=i;for(int j=0,node=i;j<m+1;j++){if((k>>j)&1){res+=f[node][j];node=g[node][j];} }ans=max(ans,res);}return ans;}
};相关文章:

Leetcode---360周赛
题目列表 2833. 距离原点最远的点 2834. 找出美丽数组的最小和 2835. 使子序列的和等于目标的最少操作次数 2836. 在传球游戏中最大化函数值 一、距离原点最远的点 这题主要是理解题意,遇到L往左走,遇到R往右走,遇到_左右都可以走&#x…...
CocosCreator3.8研究笔记(三)CocosCreator 项目结构说明及编辑器的简单使用
我们通过Dashboard 创建一个2d项目,来演示CocosCreator 的项目结构。 等待创建完成后,会得到以下项目工程: 一、assets文件夹 assets文件夹:为资源目录,用来存储所有的本地资源,如各种图片,脚本…...

html5学习笔记18-web存储、web sql、web worker
https://www.runoob.com/html/html5-webstorage.html HTML5 web 存储,可替代 cookie 的本地存储方式。 客户端存储数据的两个对象:localStorage网站的 sessionStorage窗口的 localStorage.setItem("sitename", "菜鸟教程"); // 存…...

大数据专业毕业能从事什么工作
大数据从业领域很宽广,不管是科技领域还是食品产业,零售业等都是需要大数据人才进行大数据的处理,以提供更好的用户体验,优化库存降低成本预测需求。 大数据开发做什么? 大数据开发分两类,编写Hadoop、Spa…...
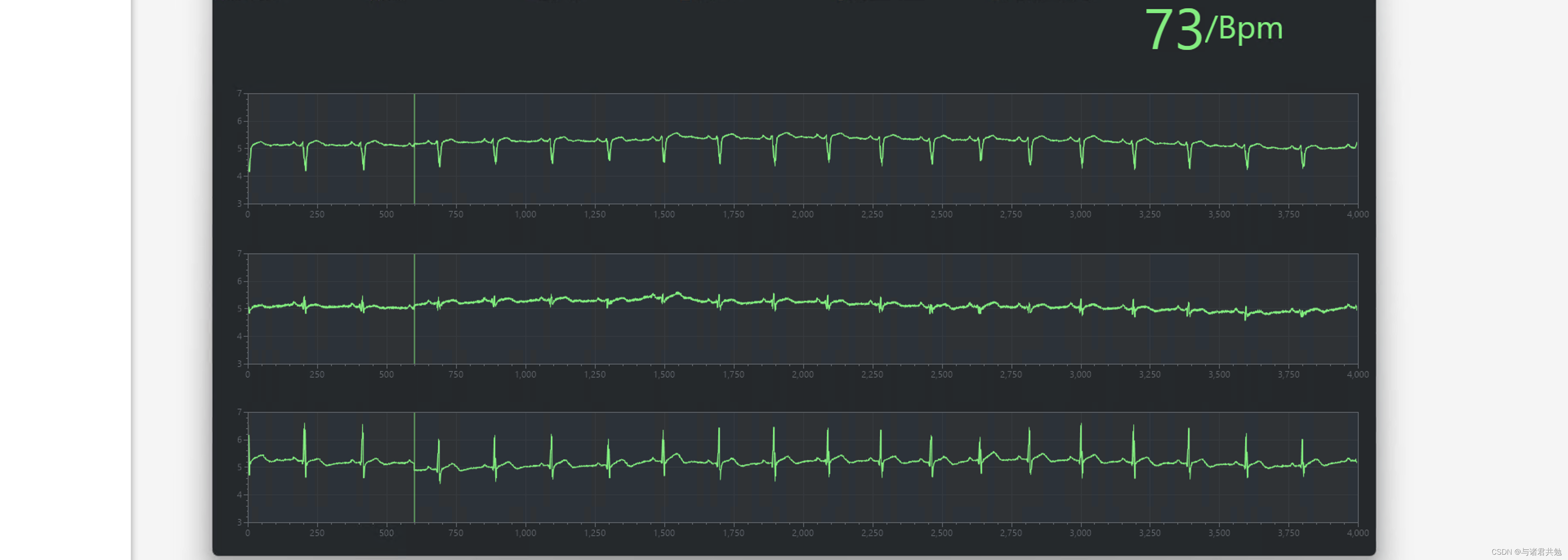
avalonia、WPF使用ScottPlot动态显示ECG心电图
文章目录 avalonia、WPF使用ScottPlot动态显示ECG心电图实现效果,动态效果懒得录视频了安装代码部分UpdateData方法就是用来更新心电图表的方法, 根据消息队列数据去更新是视图中的ScottPlot 图表 avalonia、WPF使用ScottPlot动态显示ECG心电图 avalonia…...

国内数学公式识别软件对比
1. 超级公式 官网 https://www.ocrmath.com/ 目前超级公式最好用 2. 极度公式 官网 https://jidugs.wrste.com/ 季度公式也还可以,之前提了一些改进用户建议,很久都不改,遂改用超级公式 3. SimpleTex 官网 https://simpletex.cn/ 最近才…...

SCOPE_IDENTITY什么意思
在关系型数据库中,SCOPE_IDENTITY()是一个用于获取最近插入的行的自增标识列值的函数。当向数据库表中插入一行数据时,如果表中的某列被配置为自增标识列(通常是主键列),数据库会自动为每个插入的行分配一个唯一的值&a…...

构建现代应用:Java中的热门架构概览
文章目录 1. 三层架构2. Spring框架3. 微服务架构4. Java EE(Enterprise Edition)5. 响应式架构6. 大数据架构7. 领域驱动设计(Domain-Driven Design,DDD)8. 安卓开发架构结论 🎉欢迎来到Java学习路线专栏~…...

Axure RP软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 Axure RP是一款专业的原型设计工具,它能够帮助用户创建高保真度的交互式原型。 Axure RP具有以下特点: 强大的交互设计功能:Axure RP提供了丰富的交互设计工具,用户可以通过拖拽和…...

关于微信小程序的生命周期
关于微信小程序的生命周期 onLaunch 官网App.vue/App.uvue | uni-app官网 问题描述:我现在有个小程序 取名为a 有个用户b 从来没有打开过小程序 那么他第一次打开小程序的时候会触发onLaunch 然后用户b退出了小程序 那么用户 b重新打开小程序的时候会触发 onL…...

【数据结构】带头双向循环链表及其实现
目录 1.带头双向循环链表 2.带头双向循环链表实现 2.1初始化 2.2销毁 2.3头插 2.4链表打印 2.5头删数据 2.6尾插数据 2.7尾删数据 2.8链表判空 2.9查找一个数据 2.10在pos位置前插入数据 2.11删除pos位置 2.12求链表的长度 2.顺序表和链表的比较 1.带头双向循环…...
问道管理:日换手率达20是好是坏?
关于股票商场的出资者而言,日换手率是一个非常重要的目标。日换手率是指股票当日买卖量与该股总股本之比。假如一只股票的日换手率过高,那么就意味着该股票的流动性较强,而假如日换手率过低,那么就意味着该股票的流动性较弱。 那…...

勃艮第葡萄酒是如何分级的?
勃艮第葡萄酒来自一个同名的地区:勃艮第,它位于法国中东部,在西部的卢瓦尔河和东部的索恩河之间。该地区最大的城市是欧塞尔、第戎、马孔和内韦尔。由于地处国家中心,勃艮第属于大陆性气候,夏季炎热,冬季寒冷。这种气候…...
使用awvs进行web安全扫描
1、安装 docker pull secfa/docker-awvs docker run -it -d -name awvs -p 13443:3443 --cap-add LINUX_IMMUTABLE secfa/docker-awvs2、账号密码 # https://ip:13443/ # 用户名:adminadmin.com # 密码:Admin1233、使用 ps:需要征得甲方的同意...
抖音小程序开发教学系列(1)- 抖音小程序简介
章节一:抖音小程序简介 1.1 抖音小程序的背景和概述 抖音小程序的发展背景和市场趋势: 抖音作为一款热门的短视频社交平台,用户群体庞大,社交共享的特性也为小程序的发展提供了广阔的空间。抖音小程序作为抖音在社交和用户粘性…...

【4.Vue兄弟组件之间传值-Bus总线】
1.概述 通过创建一个新的vm对象,专门统一注册事件,供所有组件共同操作,达到所有组件随意隔代传值的效果 也就是:各个组件内部要传输的数据或者要执行的命令信息,靠bus来通信。 2. 代码实现 2.1 全局引入 全局引入的话,就直接在main.js里面引入即可: // 创建 bus总线 V…...

element中Notification组件(this.$notify)自定义样式
1、自定义样式效果 2、vue代码 this.notifications this.$notify({title: ,dangerouslyUseHTMLString: true,duration: obj.remindMethod3 ? 0:4500,customClass: notify-warning,offset: 50,showClose: false,message: this.$createElement("div",null,[this.$…...

Manjaro安装使用
Manjaro安装使用 1.先更改镜像源:sudo pacman-mirrors -c China -g 2.安装第三方软件管理工具 :sudo pacman -Sy yay 导入GPG Key sudo pacman -Syy && sudo pacman -S archlinuxcn-keyring安装输入法 sudo pacman -S fcitx-im (#默认全部安装…...

【iOS】折叠cell
文章目录 前言一、实现效果二、折叠cell的实现原理三、实现折叠cell的高度变化四、实现选中点击的单元格总结 前言 在暑假的3GShare中用到了折叠cell控件,特此总结博客记录 一、实现效果 二、折叠cell的实现原理 首先我们需要知道ScrollView的是TableView的父类&a…...

无涯教程-Android - DatePicker函数
Android Date Picker允许您在自定义用户界面中选择由日,月和年组成的日期。为此功能,android提供了DatePicker和DatePickerDialog组件。 在本教程中,我们将通过DatePickerDialog演示日期选择器的用法, DatePickerDialog是一个包含DatePicker的简单对话框。 为了显示DatePicker…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
