代码随想录 - Day30 - 修剪二叉树,转换二叉树 + 二叉树总结
代码随想录 - Day30 - 修剪二叉树,转换二叉树 + 二叉树总结
669. 修剪二叉搜索树
有点像是删除二叉搜索树的变形,改变了删除条件而已。
递归法:
class Solution:def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:if not root:return rootif root.val < low: # 当前节点小于low,不用再看其左子树,遍历其右子树即可right = self.trimBST(root.right, low, high)return rightif root.val > high: # 当前节点大于high,不用再看其右子树,遍历其左子树即可left = self.trimBST(root.left, low, high)return leftroot.left = self.trimBST(root.left, low, high) # root.left接入符合条件的左孩子root.right = self.trimBST(root.right, low, high) # root.right接入符合条件的右孩子return root
迭代法:
'''
在剪枝的时候,可以分为三步:
将root移动到[L, R] 范围内,注意是左闭右闭区间
剪枝左子树
剪枝右子树
'''
class Solution:def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:if not root:return root# 处理头节点,把头结点放到[low, high]范围内while root and (root.val < low or root.val > high):if root.val < low: # 小于low往右走root = root.rightelse: # 大于high往左走root = root.leftcurleft, curright = root, root# 处理左孩子元素小于low的情况while curleft:while curleft.left and curleft.left.val < low:curleft.left = curleft.left.rightcurleft = curleft.left# 处理右孩子元素大于high的情况while curright:while curright.right and curright.right.val > high:curright.right = curright.right.leftcurright = curright.rightreturn root
108. 将有序数组转换为二叉搜索树
对于奇数长度的数组可以直接取中点,对于偶数长度的数组则需要用mid = int(left + ((right - left) / 2))。
中点作为根节点,左右两侧则分别为左子树和右子树,依次进行递归遍历。
class Solution:# 左闭右闭区间[left, right]def traversal(self, nums, left, right):if left > right:return Nonemid = int(left + ((right - left) / 2)) # 防止越界root = TreeNode(nums[mid])root.left = self.traversal(nums, left, mid - 1)root.right = self.traversal(nums, mid + 1, right)return rootdef sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:root = self.traversal(nums, 0, len(nums) - 1)return root
迭代法:用队列模拟递归过程
from collections import dequeclass Solution:def sortedArrayToBST(self, nums: List[int]) -> TreeNode:if len(nums) == 0:return Noneroot = TreeNode(0) # 初始根节点nodeQue = deque() # 放遍历的节点leftQue = deque() # 保存左区间下标rightQue = deque() # 保存右区间下标nodeQue.append(root) # 根节点入队列leftQue.append(0) # 0为左区间下标初始位置rightQue.append(len(nums) - 1) # len(nums) - 1为右区间下标初始位置while nodeQue:curNode = nodeQue.popleft()left = leftQue.popleft()right = rightQue.popleft()mid = left + (right - left) // 2curNode.val = nums[mid] # 将mid对应的元素给中间节点if left <= mid - 1: # 处理左区间curNode.left = TreeNode(0)nodeQue.append(curNode.left)leftQue.append(left)rightQue.append(mid - 1)if right >= mid + 1: # 处理右区间curNode.right = TreeNode(0)nodeQue.append(curNode.right)leftQue.append(mid + 1)rightQue.append(right)return root
538. 把二叉搜索树转换为累加树
题目中的累加是右中左的顺序进行累加,从最大的节点值累加到最小的节点值。
所以要反中序遍历该二叉树,然后顺序累加。
需要一个pre指针记录当前节点的前一个节点,这样才能方便累加。
class Solution:def traversal(self, cur): # 右中左遍历if not cur: # 终止条件returnself.traversal(cur.right) # 右cur.val += self.pre # 中self.pre = cur.valself.traversal(cur.left) # 左def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:self.pre = 0 # 记录前一个节点的数值self.traversal(root)return root
或者写成这样也可以:
class Solution:def __init__(self): # 记录前一个节点的数值self.pre = 0def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if not root: # 终止条件returnself.convertBST(root.right) # 右root.val += self.pre # 中self.pre = root.valself.convertBST(root.left) # 左return root
迭代法:
class Solution:def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if not root: return rootstack = []result = []cur = rootpre = 0 # 记录前一个节点的数值while cur or stack:if cur: # 右stack.append(cur)cur = cur.rightelse: cur = stack.pop() # 中cur.val+= prepre = cur.valcur =cur.left # 左return root
总结
二叉树这块的题目大部分可以通过递归和迭代两种方式来解决。
当遇到二叉搜索树时,可以利用其特性来简化代码。
对不同题目选择合适的遍历方式:
- 涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
- 求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
- 求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
二叉树的遍历方式(递归和迭代)+层序遍历,必须要掌握。
要知道深度优先(前中后序遍历)和广度优先(层序遍历)对应哪些遍历方式。
关键是要掌握解决问题的方法,熟悉代码,理解题目。
二叉树的题就先做到这里,今天再看一下回溯算法的基础,明天开始做题。
相关文章:

代码随想录 - Day30 - 修剪二叉树,转换二叉树 + 二叉树总结
代码随想录 - Day30 - 修剪二叉树,转换二叉树 二叉树总结 669. 修剪二叉搜索树 有点像是删除二叉搜索树的变形,改变了删除条件而已。 递归法: class Solution:def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> O…...

[音视频] sdl 渲染到外部创建的窗口上
API SDL_CreateWindowFrom # 在外部窗口上创建窗口 其他 api 调用,按照之前的 代码 ui.setupUi(this); sdl_width ui.label->width(); sdl_height ui.label->height(); SDL_Init(SDL_INIT_VIDEO); sdl_win SDL_CreateWindowFrom((void*)ui.label->wi…...

MongoDB之索引
大数据量使用全集合查询,这是非常影响性能的,而索引可以加快查询效率,提高性能,所以这方面的知识也是必不可少的。 查询分析 explain()可以帮助我们分析查询语句性能。 语法 db.collection.find(...).explain()案例及结果 案…...

Redis的介绍
Redis的架构介绍如下: 1. 概述 Redis是一个基于内存的高性能NoSQL键值数据库,支持网络访问和持久化特性。 2. 功能架构 Redis提供字符串、哈希、列表、集合、有序集合、位数组等多种数据结构,支持事务、Lua脚本、发布订阅、流水线等功能。 3. 技术架构 Redis使用单线程的…...

一文了解Docker的用法
一、什么是Docker Docker 是一个开源的应用容器引擎,基于 Go 语言 并遵从 Apache2.0 协议开源。 Docker 可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发布到任何流行的 Linux 机器上,也可以实现虚拟化。 容器是…...

netcat的使用
目录 netcat简介 nc的使用场景 nc实现通信 创建一个服务端 创建一个客户端 具体案例 环境 win10在具体路径下执行命令 win7在具体路径下执行命令 netcat文件传输 nc文件传输的利用 服务器等待接收文件 客户端向服务器发送文件 服务器向连接的客户端发送文件 客户…...

深度学习推荐系统(二)Deep Crossing及其在Criteo数据集上的应用
深度学习推荐系统(二)Deep Crossing及其在Criteo数据集上的应用 在2016年, 随着微软的Deep Crossing, 谷歌的Wide&Deep以及FNN、PNN等一大批优秀的深度学习模型被提出, 推荐系统全面进入了深度学习时代, 时至今日,…...

前端常用 Vue3 项目组件大全
Vue.js 是一种流行的 JavaScript 前端框架,它简化了构建交互式的用户界面的过程。Vue3 是 Vue.js 的最新版本,引入了许多新的特性和改进。在 Vue3 中,组件是构建应用程序的核心部分,它们可以重用、组合和嵌套。下面是一些前端开发…...
javaee spring 静态代理
静态代理 package com.test.staticProxy;public interface IUsersService {public void insert(); }package com.test.staticProxy;//目标类 public class UsersService implements IUsersService {Overridepublic void insert() {System.out.println("添加用户");…...

Java 包装类和Arrays类(详细解释)
目录 包装类 作用介绍 包装类的特有功能 Arrays类 Arrays.fill() Arrays.toString() Arrays.sort() 升序排序 降序排序 Arrays.equals() Arrays.copyOf() Arrays.binarySearch() 包装类 作用介绍 包装类其实就是8种基本数据类型对应的引用类型。 基本数据类型引用…...
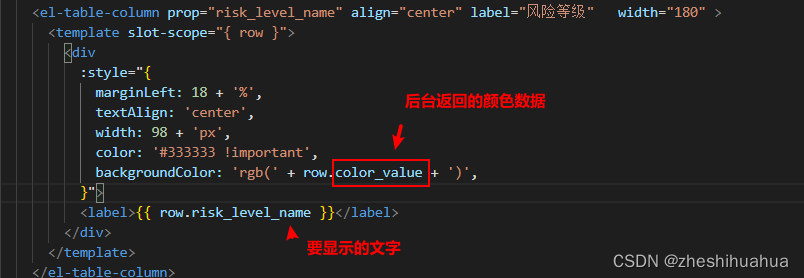
elementUi中的el-table表格的内容根据后端返回的数据用不同的颜色展示
效果图如下: 首先 首先:需要在表格行加入 <template slot-scope"{ row }"> </template>标签 <el-table-column prop"usable" align"center" label"状态" width"180" ><templ…...

在访问一个网页时弹出的浏览器窗口,如何用selenium 网页自动化解决?
相信大家在使用selenium做网页自动化时,会遇到如下这样的一个场景: 在你使用get访问某一个网址时,会在页面中弹出如上图所示的弹出框。 首先想到是利用Alert类来处理它。 然而,很不幸,Alert类处理的结果就是没有结果…...

python 基于http方式与基于redis方式传输摄像头图片数据的实现和对比
目录 0. 需求1. 基于http方式传递图片数据1.1 发送图片数据1.2 接收图片数据并可视化1.3 测试 2. 基于redis方式传递图片数据2.1 发送图片数据2.2 接收图片数据并可视化2.3 测试 3. 对比 0. 需求 在不同进程或者不同语言间传递摄像头图片数据,比如从java实现的代码…...

快速使用Git完整开发
本系列有两篇文章: 一是本篇,主要说明了关于Git工具的基础使用,包含三板斧(git add、git commit、git push)、Git基本配置、版本回退、分支管理、公钥与私钥、远端仓库和远端分支、忽略文件、命令别名、标签等内容。二…...

鲁棒优化入门(7)—Matlab+Yalmip两阶段鲁棒优化通用编程指南(下)
0.引言 上一篇博客介绍了使用Yalmip工具箱求解单阶段鲁棒优化的方法。这篇文章将和大家一起继续研究如何使用Yalmip工具箱求解两阶段鲁棒优化(默认看到这篇博客时已经有一定的基础了,如果没有可以看看我专栏里的其他文章)。关于两阶段鲁棒优化与列与约束生成算法的原…...
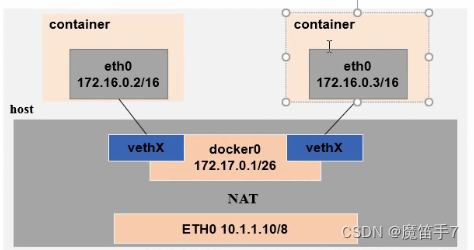
Docker技术--Docker中的网络问题
1.docker中的网络通信 如果想要弄清楚docker中的网络通信问题,其实需要弄清楚这几个问题就可以:容器与容器之间的通信、容器与外部网络之间的通信、外部网络与容器之间的通信。 -a:容器与容器之间的通信,如下所示: 在默认情况下,docker使用网桥(Bridge模式)与NAT通信。这…...

ASP.NET Core 中的两种 Web API
ASP.NET Core 有两种创建 RESTful Web API 的方式: 基于 Controller,使用完整的基于ControllerBase的基类定义接口endpoints。基于 Minimal APIs,使用Lambda表达式定义接口 endpoints。 基于 Controller 的 Web API 可以使用构造函数注入&a…...
【线程池】如何判断线程池中的任务执行完毕(三)
目录 前言 1. isTerminated()方法 2. awaitTermination()方法 3.getTaskCount()方法和executor.getCompletedTaskCount()方法结合使用 4.使用CountDownlatch类 前言 通常我们使用线程池的时候,系统处于运行的状态,而线程池本身就是主要为了线程复用&…...

Qt/C++编写视频监控系统81-Onvif报警抓图和录像并回放
一、前言 视频监控系统中的图文警情模块,是通过Onvif协议的事件订阅拿到的,通过事件订阅后,设备的各种报警事件比如入侵报警/遮挡报警/越界报警/开关量报警等,触发后都会主动往订阅者发送,而且一般都是会发送两次&…...

浅谈安防视频监控平台EasyCVR视频汇聚平台对于夏季可视化智能溺水安全告警平台的重要性
每年夏天都是溺水事故高发的时期,许多未成年人喜欢在有水源的地方嬉戏,这导致了悲剧的发生。常见的溺水事故发生地包括水库、水坑、池塘、河流、溪边和海边等场所。 为了加强溺水风险的提示和预警,完善各类安全防护设施,并及时发现…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
