知识储备--基础算法篇-数组
1.学习
2.数组
2.1第53题-最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
心得:一直在纠结这个连续的事情,最后发现根本没必要管,因为如果前一个数与当前数相加小于当前数,前面的部分就会直接被舍弃,如果相加大于当前数则会一直叠加。
class Solution(object):def maxSubArray(self, nums):""":type nums: List[int]:rtype: int"""dp = copy.deepcopy(nums)max_ = dp[0]for i in range(1,len(nums)):dp[i] = max(dp[i-1]+nums[i], dp[i])if max_ < dp[i]:max_ = dp[i]return max_
时间和内存占用太多,根本没必要再生成一个dp数组,直接用nums数组更新就行。
class Solution(object):def maxSubArray(self, nums):""":type nums: List[int]:rtype: int"""# dp = copy.deepcopy(nums)max_ = nums[0]for i in range(1,len(nums)):nums[i] = max(nums[i-1]+nums[i], nums[i])if max_ < nums[i]:max_ = nums[i]return max_ 
2.2第56题-合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]] 输出:[[1,6],[8,10],[15,18]] 解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]] 输出:[[1,5]] 解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
class Solution(object):def merge(self, intervals):""":type intervals: List[List[int]]:rtype: List[List[int]]"""new_int = []a = []intervals.sort()for i in range(1,len(intervals)):# 前一个end大于后一个startif intervals[i-1][1] > intervals[i][0]:# 前一个end小于后一个endif intervals[i-1][1] <= intervals[i][1]:intervals[i] = [intervals[i-1][0], intervals[i][1]]else:intervals[i] = intervals[i-1]elif intervals[i-1][1] == intervals[i][0]:intervals[i] = [intervals[i-1][0], intervals[i][1]]else:new_int.append(intervals[i-1])new_int.append(intervals[-1])return new_int
2.3第189题-轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]
class Solution(object):def rotate(self, nums, k):""":type nums: List[int]:type k: int:rtype: None Do not return anything, modify nums in-place instead."""# if k == 0:# return numsnums1 = copy.deepcopy(nums)k = k % len(nums)start = len(nums)-k# nums2 = []# nums1 = nums[:start]# nums2 = nums[start:]for i in range(len(nums)):if i < k:nums[i] = nums[start+i]else:nums[i] = nums1[i-k]
感觉不用深拷贝整个数组
class Solution(object):def rotate(self, nums, k):""":type nums: List[int]:type k: int:rtype: None Do not return anything, modify nums in-place instead."""k = k % len(nums)start = len(nums)-knums1 = nums[:start]nums2 = nums[start:]for i in range(len(nums2)):nums[i] = nums2[i]for j in range(len(nums1)):nums[j+k] = nums1[j]
看了答案,发现我最早想出的方法就是最简单的答案,nums[:]=nums[start:]+nums[:start],但是发现一直不能修改nums的值,看了答案发现nums忘记加[:]了,吐了。
class Solution(object):def rotate(self, nums, k):""":type nums: List[int]:type k: int:rtype: None Do not return anything, modify nums in-place instead."""k = k % len(nums)start = len(nums)-knums[:] = nums[start:] + nums[:start]
2.4除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums =[1,2,3,4]输出:[24,12,8,6]
先用最简单的遍历法,果然超时。
class Solution(object):def productExceptSelf(self, nums):""":type nums: List[int]:rtype: List[int]"""len_ = len(nums)answer = [1]*len_for i in range(len_):for j in range(len_):if j != i:answer[i] = answer[i]*nums[j]return answer然后把数组分为i点的前半部分和后半部分相乘来计算,这样的话减少很多重复计算的时间。
class Solution(object):def productExceptSelf(self, nums):""":type nums: List[int]:rtype: List[int]"""# 可以把乘积分为前半部分和后半部分len_ = len(nums)answer = [1]*len_forward = [1]*len_back = [1]*len_for i in range(1,len_):forward[i] = forward[i-1]*nums[i-1]for j in reversed(range(len_-1)):back[j] = back[j+1]*nums[j+1]for k in range(len_):answer[k] = forward[k]*back[k]return answer
看了答案,知道了左边的乘积其实可以动态的变化
class Solution(object):def productExceptSelf(self, nums):""":type nums: List[int]:rtype: List[int]"""# 可以把乘积分为前半部分和后半部分len_ = len(nums)answer = [1]*len_back = 1for i in range(1,len_):answer[i] = answer[i-1]*nums[i-1]for j in reversed(range(len_)):answer[j] = answer[j]*backback = back * nums[j]return answer
2.5第41题-缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0] 输出:3
用最朴素的方法来寻找,不出所料,超时。
class Solution(object):def firstMissingPositive(self, nums):""":type nums: List[int]:rtype: int"""for i in range(len(nums)-1):j = 0while j < len(nums)-1-i:if nums[j] > nums[j+1]:temp = nums[j]nums[j] = nums[j+1]nums[j+1] = tempj = j + 1# print(nums)if nums[-1] <= 0:return 1index_1 = 0for j in range(len(nums)):if nums[j] > 0:if nums[j] != 1:return 1else:index_1 = jbreaka = 1# print(index_1)for k in range(index_1+1,len(nums)):a = a + 1if nums[k] == a:continueelif nums[k] == a-1:a = a - 1continueelse:return areturn a + 1看了解析,知道当nums长度为N时,正数的数目肯定在[1,N]范围内,这时候就可以用哈希表来查找,内存占用多但速度快。把nums中的数都放在哈希表中,然后遍历[1,N],如果有哈希表中不存在则返回i,若都存在则返回i+1。
class Solution(object):def firstMissingPositive(self, nums):""":type nums: List[int]:rtype: int"""hash_table = set(nums)n = len(nums)a = 0for i in range(1,n+1):if i in hash_table:a = icontinueelse:return ireturn a + 1
相关文章:

知识储备--基础算法篇-数组
1.学习 2.数组 2.1第53题-最大子数组和 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 心得:一直在纠结这个连续的事情&…...
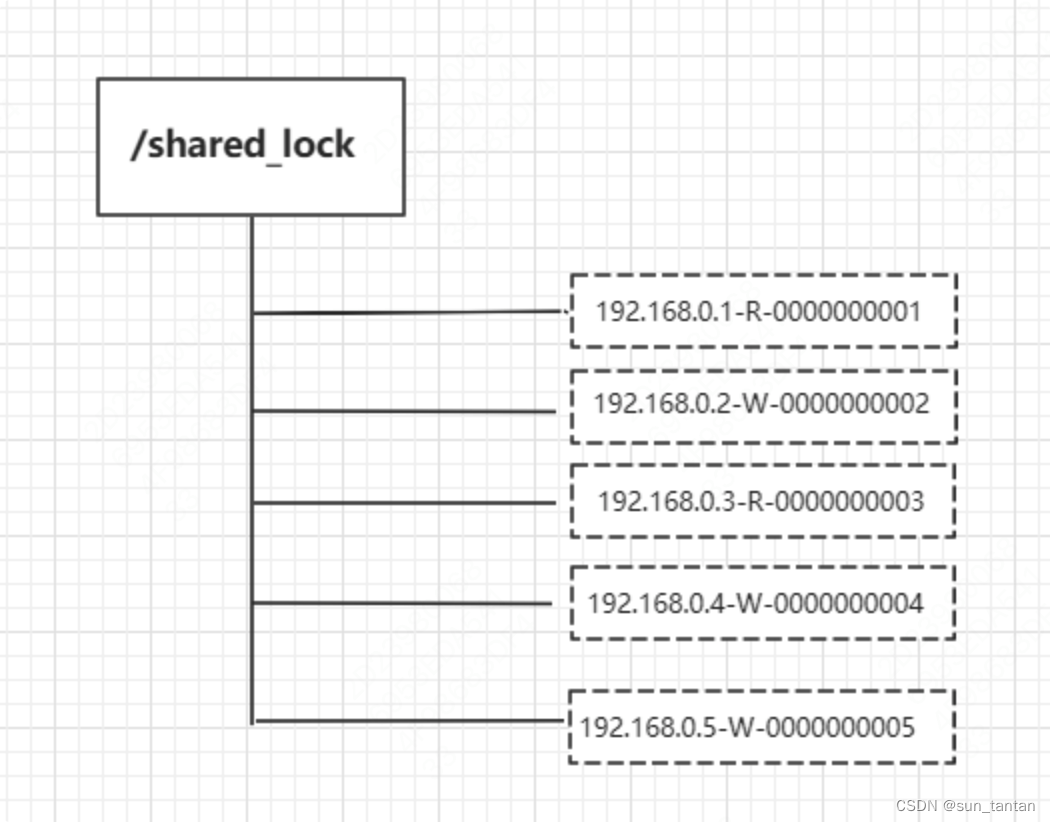
zookeeper 理论合集
目录 系统背景 集群结构 多个节点之间的角色 节点的状态 为什么引入 Observer 存储结构 ZNode 节点结构 ZNode 创建类型 内存数据存储 数据持久化 zookeeper 的容量大小 数据同步 消息广播 崩溃恢复 如何保证顺序一致性 核心流程 Leader 选举流程 脑裂问题 …...
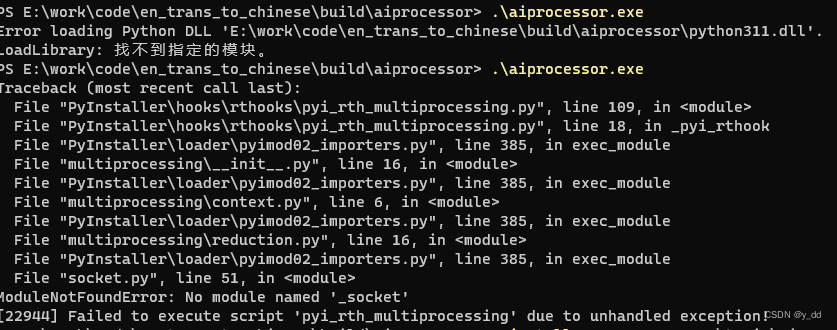
【pyinstaller 怎么打包python,打包后程序闪退 不打日志 找不到自建模块等问题的踩坑解决】
程序打包踩坑解决的所有问题 问题1 多个目录怎么打包 不管你包含多个层目录,引用多么复杂,只需要打包主程序所在文件即可,pyinstaller会自动寻找依赖包,如果报错自建模块找不到,参照问题3 pyinstaller main.py问题2…...
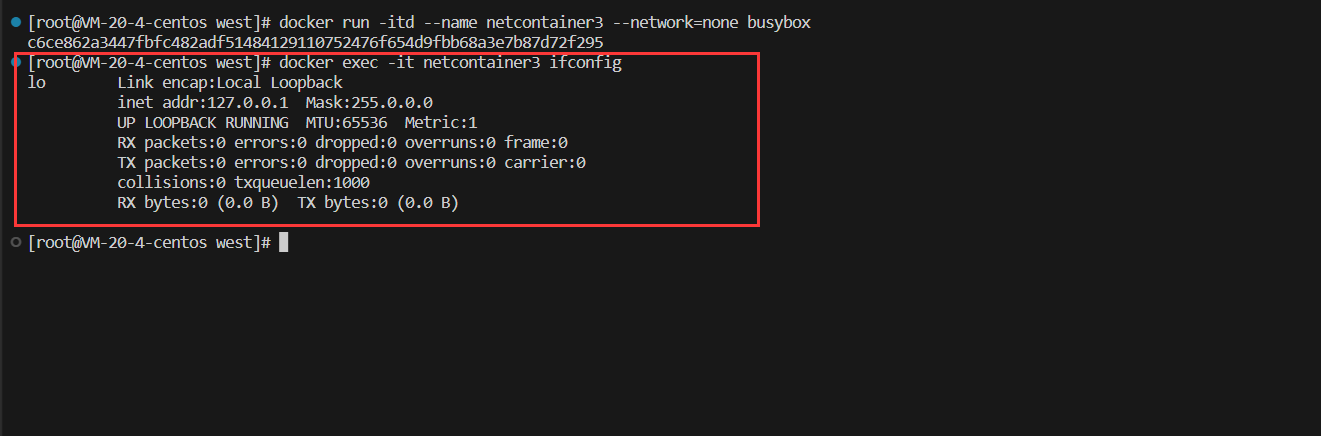
【Docker】网络
文章目录 Docker 网络基础Docker网络管理Docker网络架构CNMLibnetwork驱动 常见的网络类型 Docker 网络管理命令docker network createdocker network inspectdocker network connectdocker network disconnectdocker network prunedocker network rmdocker network ls docker …...

Linux :realpath 命令
以后可以直接用于查找相关文件 例: 输入:realpath .repo/manifests/rv1126_rv1109_linux_release.xml 输出:/home/sdk/work/rk/rv1126_rv1109/.repo/manifests/rv1126_rv1109_linux/rv1126_rv1109_linux_v3.0.2_20230406.xml根据输入的文件找到对应复制过来的型号,这个命令不…...

react17:生命周期函数
挂载时更新时 setState触发更新、父组件重新渲染时触发更新forceUpdate触发更新卸载时 react(v17.0.2)的生命周期图谱如下。 相较于16版本,17版本生命周期函数有如下变化: componentWillMount() componentWillUpdate() compone…...

腾讯内部单边拥塞算法BBR-TCPA一键脚本安装
TCPA简介 腾讯内部使用的TCPA,由腾讯TEG操作系统组研发,基于RHEL7.4源码,定制化的TCPA。团队介绍:腾讯TEG操作系统组, 2010年成立,专业的内核团队,维护研发腾讯内部linux操作系统tlinux, 保证百万级server高效稳定运行…...
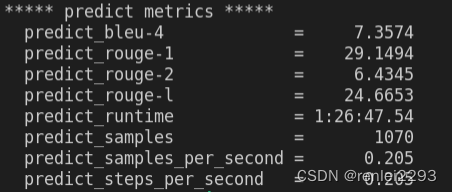
【LLM】chatglm-6B模型训练和推理
本篇文章记录下 chatglm-6B 训练和推理过程 环境:Ubuntu 20.04 1.13.0cu116 chatglm-6B 源代码仓库:链接 chatglm-6B 模型权重:链接 源代码及模型 clone 到本地 这里使用的是 THUDM 在 hugging face 开源的模型。 因为模型比较大ÿ…...

性能可靠it监控系统,性能监控软件的获得来源有哪些
性能可靠的IT监控系统是企业IT运维的重要保障之一。以下是一个性能可靠的IT监控系统应该具备的特点: 高可用性 高可用性是IT监控系统的一个重要特点,它可以保证系统在24小时不间断监控的同时,保证系统服务的可用性和稳定性。为了实现高可用性…...
 理解网络编程和套接字)
TCP/IP网络编程(一) 理解网络编程和套接字
文章目录 理解网络编程和套接字网络编程和套接字概要构建套接字编写 Hello World 服务器端构建请求连接套接字在Linux平台下运行 基于Linux的文件操作打开文件关闭文件将数据写入文件读取文件中的数据 理解网络编程和套接字 网络编程和套接字概要 网络编程就是编写程序使两台…...

Python 潮流周刊#18:Flask、Streamlit、Polars 的学习教程
你好,我是猫哥。这里每周分享优质的 Python、AI 及通用技术内容,大部分为英文。标题取自其中三则分享,不代表全部内容都是该主题,特此声明。 本周刊由 Python猫 出品,精心筛选国内外的 250 信息源,为你挑选…...

装备一台ubuntu
配置远程连接: ubuntu的root用户无法远程登入问题: openssh安装命令: sudo apt-get install openssh-server 安装完成通过以下命令查看SSH是否启动 ps -e | grep ssh 如果只有ssh-agent表示还没启动,需要: /etc/i…...
为了更好和大家交流,欢迎大家加我的微信账户
因为一些懂的都懂的原因,如果我的账户显示为 此时我无法通过站内信、留言或者任何方式和大家联系。 如果看到这样的内容,可以在此评论区留下你的微信账户,我看到后会添加你。为防止其他人冒充我,我的微信号以2206结尾。...

MS1826A HDMI 多功能视频处理器 HDMI4进1出画面分割芯片
基本介绍 MS1826A 是一款多功能视频处理器,包含 4 路独立 HDMI 音视频输入通道、1 路 HDMI 音视 频输出通道以及 1 路独立可配置为输入或者输出的 SPDIF、I2S 音频信号。支持 4 个独立的字库定 制型 OSD;可处理隔行和逐行视频或者图形输入信号࿱…...

最新文献怎么找|学术最新前沿文献哪里找
查找下载最新文献最好、最快、最省事的方法就是去收录该文献的官方数据库中下载。举例说明: 有位同学求助下载一篇2023年新文献,只有DOI号10.1038/s41586-023-06281-4,遇到这种情况可以在DOI号前加上http://doi.org/输入地址栏查询该文献的篇…...

ctfshow 红包题
前言: 最近一直在搞java很少刷题,看见ctfshow的活动赶紧来复现一波~ ctfshow 红包挑战7 <?php highlight_file(__FILE__); error_reporting(2); extract($_GET); ini_set($name,$value); system("ls ".filter($_GET[1])."" )…...
SpringBoot项目(jar)部署,启动脚本
需求 SpringBoot项目(jar)部署,需要先关闭原来启动的项目,再启动新的项目。直接输入命令,费时费力,还容易出错。所以,使用脚本启动。 脚本 脚本名:start.sh 此脚本需要放置在jar包…...

大数据(四)主流大数据技术
大数据(四)主流大数据技术 一、写在前面的话 To 那些被折磨打击的好女孩(好男孩): 有些事情我们无法选择,也无法逃避伤害。 但请你在任何时候都记住: 你可能在一些人面前,一文不值&a…...

【已解决】激活虚拟环境报错:此时不应有Anaconda3\envs\[envs]\Library\ssl\cacert.pem。
新建虚拟环境后,进入虚拟环境的时候出现这样的报错: 此时不应有Anaconda3 envs yolov5 Library ssl cacert.pem。 但是之前装的虚拟环境也还能再次激活,base环境也无任何问题,仅新装的虚拟环境无法激活。 查遍了百度谷歌ÿ…...
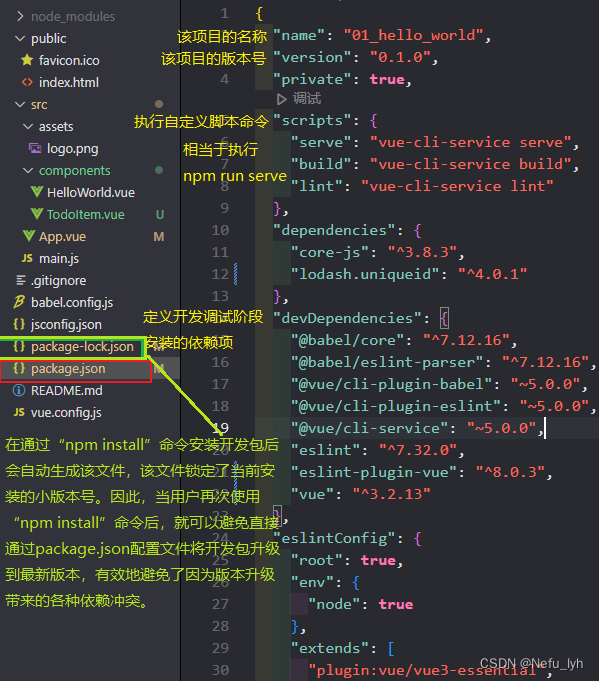
Vue安装过程的困惑解答——nodejs和vue关系、webpack、vue-cli、vue的项目结构
文章目录 1、为什么在使用vue前要下载nodejs?2、为什么安装nodejs后就能使用NPM包管理工具?3、为什么是V8引擎并且使用C实现?4、为什么会安装淘宝镜像?5、什么是webpack模板?6、什么是脚手架 vue-cli?6.1 安…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
