搭配购买——并查集+01背包
Joe觉得云朵很美,决定去山上的商店买一些云朵。
商店里有 n 朵云,云朵被编号为 1,2,…,n,并且每朵云都有一个价值。但是商店老板跟他说,一些云朵要搭配来买才好,所以买一朵云则与这朵云有搭配的云都要买。但是Joe的钱有限,所以他希望买的价值越多越好。
输入格式
第 1 行包含三个整数 n,m,w,表示有 n 朵云,m 个搭配,Joe有 w 的钱。
第 2∼n+1 行,每行两个整数 ci,di 表示 i 朵云的价钱和价值。
第 n+2∼n+1+m 行,每行两个整数 ui,vi,表示买 ui 就必须买 vi,同理,如果买 vi 就必须买 ui。
输出格式
一行,表示可以获得的最大价值。
数据范围
1≤n≤10000,0≤m≤5000,1≤w≤10000,1≤ci≤5000,1≤di≤100,1≤ui,vi≤n
输入样例:
5 3 10
3 10
3 10
3 10
5 100
10 1
1 3
3 2
4 2
输出样例:
1
解析:
搭配的都要买,可以理解成将有关系的都放在一起,相当一个物品,要买一起买。
这样就可以转换成01背包问题,每个物品只能购买一次,在有限的钱的情况下,让买的物品的价值尽可能的大。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e6+10;
int p[N];
int v[N],w[N];
int v1[N],w1[N];
int f[N];
bool vis[N];
int find(int x)
{if (x!=p[x]) p[x]=find(p[x]);return p[x];
}
signed main()
{int n,m,k;cin>>n>>m>>k;for (int i=1;i<=n;i++) p[i]=i;for (int i=1;i<=n;i++) cin>>v[i]>>w[i];for (int i=0;i<m;i++){int a,b;cin>>a>>b;int x=find(a),y=find(b);if (x!=y){v[y] +=v[x];w[y] +=w[x];p[x]=y;}}int cnt=0;for (int i=1;i<=n;i++){int x=find(i);if (!vis[x]){cnt++;v1[cnt]=v[x];w1[cnt]=w[x];vis[x]=1;}}for (int i=1;i<=cnt;i++) //01背包最简化 //模板for (int j=k;j>=v1[i];j--)f[j]=max(f[j],f[j-v1[i]]+w1[i]);cout<<f[k];return 0;
}//发现可以简化一下代码,不需要开新的数组记录每个“新的物品”的价值和代价。#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e6+10;
int p[N];
int v[N],w[N];
int f[N];
int find(int x)
{if (x!=p[x]) p[x]=find(p[x]);return p[x];
}
signed main()
{int n,m,k;cin>>n>>m>>k;for (int i=1;i<=n;i++) p[i]=i;for (int i=1;i<=n;i++) cin>>v[i]>>w[i];for (int i=0;i<m;i++){int a,b;cin>>a>>b;int x=find(a),y=find(b);if (x!=y){v[y] +=v[x];w[y] +=w[x];p[x]=y;}}for (int i=1;i<=n;i++) //01背包最简化 //模板if (p[i]==i) //每个集合的根节点{for (int j=k;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);}cout<<f[k];return 0;
}相关文章:

搭配购买——并查集+01背包
Joe觉得云朵很美,决定去山上的商店买一些云朵。 商店里有 n 朵云,云朵被编号为 1,2,…,n,并且每朵云都有一个价值。但是商店老板跟他说,一些云朵要搭配来买才好,所以买一朵云则与这朵云有搭配的云都要买。但是Joe的钱有…...
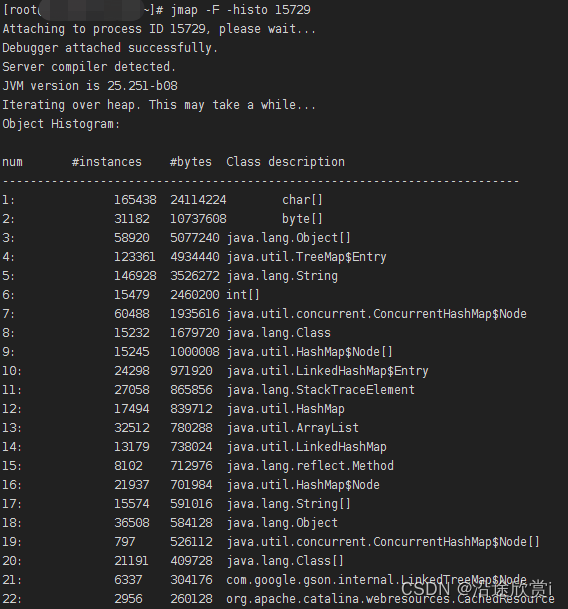
JVM调优指令参数
常用命令查找文档站点:https://docs.oracle.com/javase/8/docs/technotes/tools/unix/index.html -XX:PrintFlagsInitial 输出所有参数的名称和默认值,默认不包括Diagnostic和Experimental的参数。可以配合 -XX:UnlockDiagnosticVMOptions和-XX:UnlockEx…...

数据结构入门 — 队列
本文属于数据结构专栏文章,适合数据结构入门者学习,涵盖数据结构基础的知识和内容体系,文章在介绍数据结构时会配合上动图演示,方便初学者在学习数据结构时理解和学习,了解数据结构系列专栏点击下方链接。 博客主页&am…...
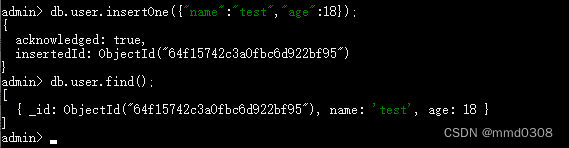
MongoDB - 安装
一、Docker安装MongoDB 1. 安装 安装版本: 7.0.0 docker run -itd --name mongodb -v C:\\data\\mongodb\\data:/data/db -p 27017:27017 mongo:7.0.0 --auth-v: 将容器目录/data/db映射到本地C:\\data\\mongodb\\data目录,防止容器删除数据丢失-p: 端口映射--aut…...
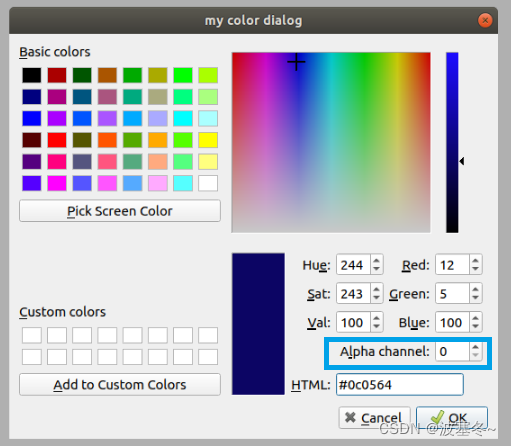
Qt应用开发(基础篇)——颜色选择器 QColorDialog
一、前言 QColorDialog类继承于QDialog,是一个设计用来选择颜色的对话框部件。 对话框窗口 QDialog QColorDialog颜色选择器一般用来让用户选择颜色,比如画图工具中选择画笔的颜色、刷子的颜色等。你可以使用静态函数QColorDialog::getColor()直接显示对…...
vscode 清除全部的console.log
在放页面的大文件夹view上面右键点击在文件夹中查找 console.log.*$ 注意:要选择使用正则匹配 替换为 " " (空字符串)...

UG\NX CAM二次开发 插入工序 UF_OPER_create
文章作者:代工 来源网站:NX CAM二次开发专栏 简介: UG\NX CAM二次开发 插入工序 UF_OPER_create 效果: 代码: void MyClass::do_it() {tag_t setup_tag=NULL_TAG;UF_SETUP_ask_setup(&setup_tag);if (setup_tag==NULL_TAG){uc1601("请先初始化加工环境…...

C++指针、指针函数、函数指针、类指针
1、指针变量 #include <iostream>using namespace std;int main () {int var 20; // 实际变量的声明int *ip; // 指针变量的声明ip &var; // 在指针变量中存储 var 的地址cout << "Value of var variable: ";cout << var …...
)
图:最短路径问题(BFS算法,Dijkstra算法,Floyd算法)
1 .单源最短路径 1.BFS算法(无权图) 使用广度优先遍历实现一个顶点到达其他所有顶点的最短路径。 注:无权图可以视为一种特殊的带权图,只是每条边的权值都为1。 1.算法思路: 定义一个数组存储每个结点与当前的结点的最短距离,定义一个数组…...
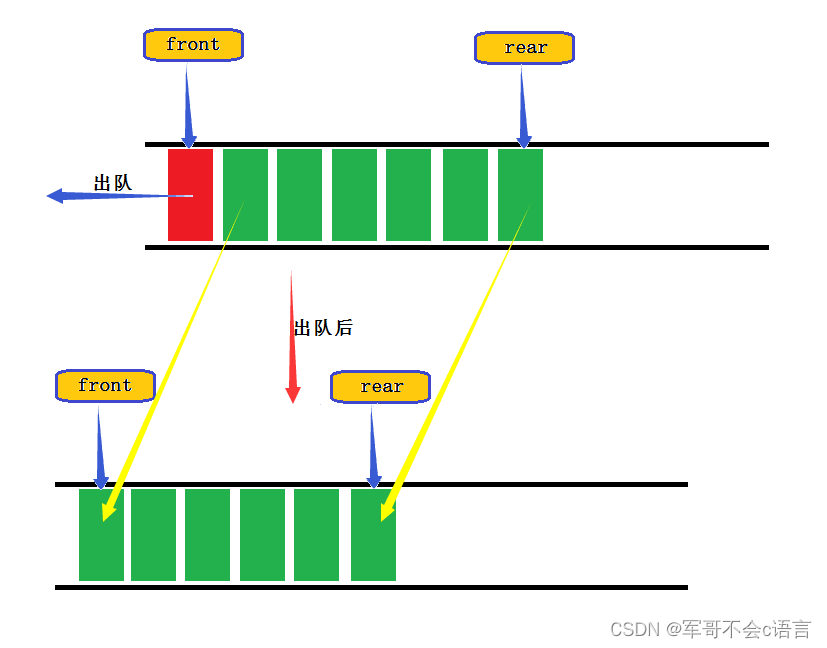
栈和队列篇
目录 一、栈 1.栈的概念及结构 1.1栈的概念 1.2栈的结构示意图 2.栈的实现 2.1支持动态增长的栈的结构 2.2压栈(入栈) 2.3出栈 2.4支持动态增长的栈的代码实现 二、队列 1.队列的概念及结构 1.1队列的概念 1.2队列的结构示意图 2.队列的实…...
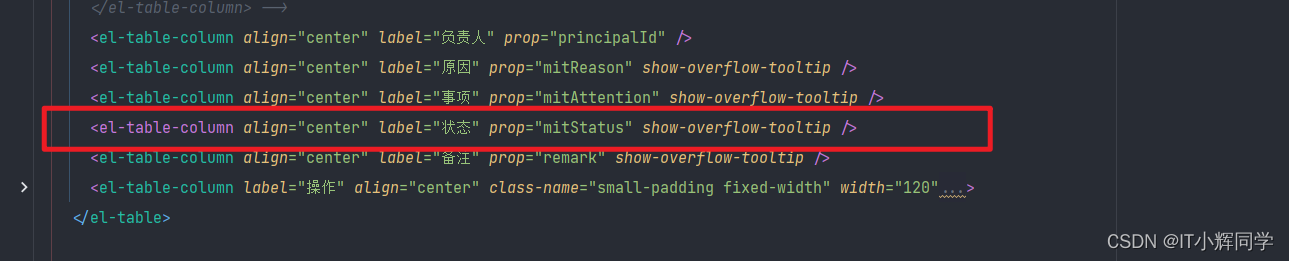
分享一个vue-slot插槽使用场景
需求再现 <el-table-column align"center" label"状态" prop"mitStatus" show-overflow-tooltip />在这里,我想对于状态进行一个三目判断,如果为0那就是进行中,否则就是已完成,期初我是这样写…...
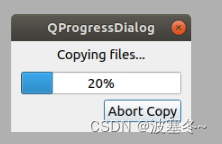
Qt应用开发(基础篇)——进度对话框 QProgressDialog
一、前言 QProgressDialog类继承于QDialog,是Qt设计用来反馈进度的对话框。 对话框QDialog QProgressDialog提供了一个进度条,表示当前程序的某操作的执行进度,让用户知道操作依旧在激活状态,配合按钮,用户就可以随时终…...

基于SpringBoot2的后台业务管理系统
概述 SpringBoot-Plus 是一个适合大系统拆分成小系统的架构,java快速开发平台,或者是一个微服务系统。其中加入了Thymeleaf数据模板语言代替了之前的JSP页面方式。页面展示采用Layui前端框架,包含了用户管理,角色管理,…...
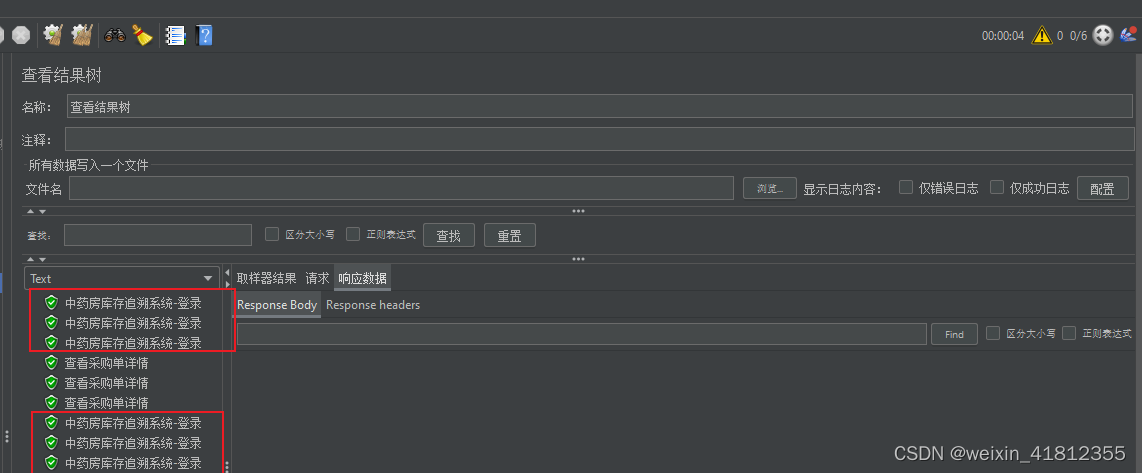
Jmeter(三十):并发测试(设置集合点)
集合点:让所有请求在不满足条件的时候处于等待状态。 如:我集合点设置为50,那么不满足50个请求的时候,这些请求都会集合在一起,处于等待状态,当达到50的时候,就一起执行。从而达到并发的效果。 那么Jmeter中可以通过同步定时器 Synchronizing Timer 来完成。 Number …...
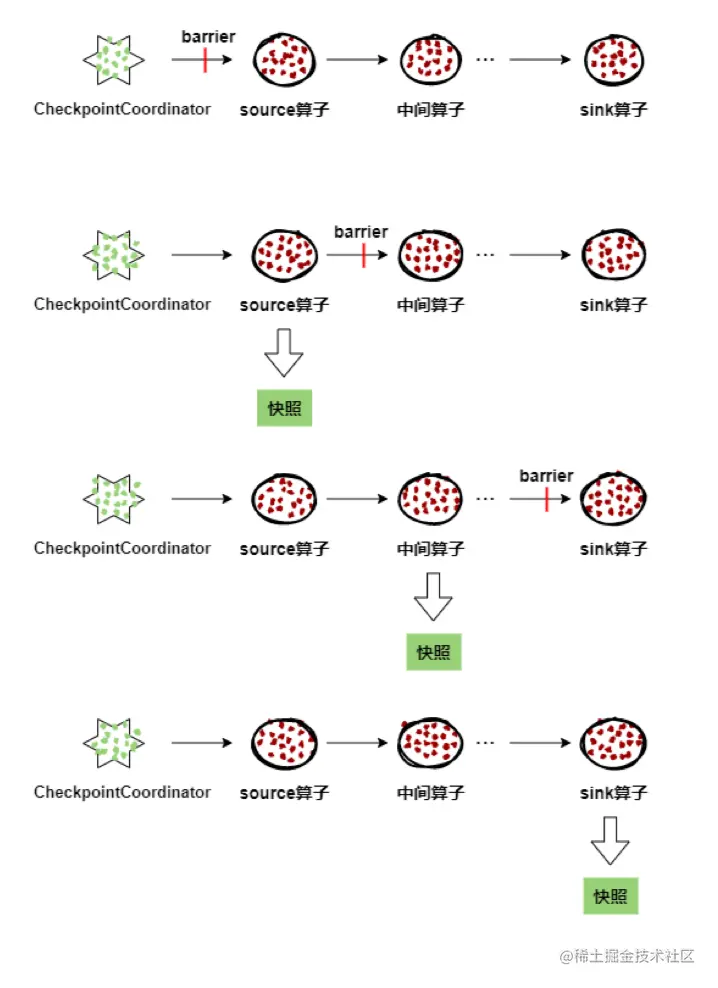
Flink的checkpoint是怎么实现的?
分析&回答 Checkpoint介绍 Checkpoint容错机制是Flink可靠性的基石,可以保证Flink集群在某个算子因为某些原因(如 异常退出)出现故障时,能够将整个应用流图的状态恢复到故障之前的某一状态,保证应用流图状态的一致性。Flink的Checkpoint机制原理来自“Chandy-Lamport alg…...

ubuntu上安装nginx
这篇文章主要介绍怎么在ubuntu上安装nginx服务器,并进行一些简单的配置。 第一步:准备好一台ubuntu操作系统的虚拟机 注意:如果你还没有安装好ubuntu,个人推荐阅读以下文章完成unbutu安装,vm的版本不用刻意安装文章中…...

9. 微积分 - 导数
文章目录 导数求导实例代码演示:迭代法求解二次函数最小值阶Hi, 大家好。我是茶桁。 我们终于结束了极限和连续的折磨,开启了新的篇章。 不过不要以为我们后面的就会很容易,只是相对来说, 没有那么绕而已。 那么,我们今天开始学习「导数」。 导数 在之前的导论,也就是…...

滑动窗口系列1-达标子数组
#达标子数组# 求达标子数组的数量 * 题目:给定一个数组,求满足子数组中最大值-最小值小于等于某个数的子数组的数量 * 例如[0,1,2,3]中求子数组中最大值-最小值小于等于 2的子数组的数量 * 结果为9,因为满足条件的只有[0,0] [0,1] [0,2] [1,1] [1,2] [1…...
)
电视显示技术及价格成本对比(2023年)
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 本文链接:https://blog.csdn.net/zaibeijixing/article/details/132461068 ———————————————— 截止到2023年ÿ…...

浅谈 Pytest+HttpRunner 如何展开接口测试!
软件测试有多种多样的方法和技术,可以从不同角度对它们进行分类。其中,根据软件生命周期,针对不同的测试对象与目标,可将测试过程分为 4 个阶段:单元测试、集成测试、系统测试和验收测试。本文着重介绍了如何借用 pyte…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...
