图:最短路径问题(BFS算法,Dijkstra算法,Floyd算法)
1 .单源最短路径
1.BFS算法(无权图)
使用广度优先遍历实现一个顶点到达其他所有顶点的最短路径。
注:无权图可以视为一种特殊的带权图,只是每条边的权值都为1。
1.算法思路:
- 定义一个数组存储每个结点与当前的结点的最短距离,
- 定义一个数组存储当前结点的前驱结点序号。
- 定义一个数组存储所有结点的访问情况:已访问为true,未访问为false。
2.代码实现:
就是对BFS的小修改:
在visit一个顶点时,修改其最短路径长度d[]并在path[]记录前驱结点
//求顶点u到其他顶点的最短路径
void BFS_MIN_Distance(Graph G, int u) {// d[i]表示从u到i结点的最短路径for (i = 0; i < G.vexnum; ++i) {d[i] = o;//初始化路径长度path[i] = -1;//最短路径从哪个顶点过来}d[u] = 0;visited[u] = TRUE;EnQueue(Q, u);while (!isEmpty(Q)) {// BFS算法主过程DeQueue(Q, u);//队头元素u出队for (w = FirstNeighbor(G, u); w >= 0; w = NextNeighbor(G, u, w))if (!visited[w]) {// w为u的尚未访问的邻接顶点d[w] = d[u] + 1;//路径长度加1path[w] = u;//最短路径应从u到wvisited[w] = TRUE;//设已访问标记EnQueue(Q, w);//顶点w入队}}
}
由广度优先遍历生成的广度优先生成树,一定是高度最小的生成树。
2.Dijkstra(迪杰斯特拉)算法(带权图、无权图)
1.分析BFS算的局限性
BFS算法求单源最短路径只适用于无权图,或所有边的权值都相同的图。
回顾知识点:
- 带权路径长度:当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度。
2.算法分析
- 第一个数组标记各顶点是否已找到最短路径,存放true或者false。
- 第二个数组记录各顶点的最短路径长度,无穷代表暂没找到最短路径。
- 第三个数组记录各个结点最短路径上的直接前驱。
3.算法步骤
- 第1轮︰循环遍历所有结点,找到还没确定最短路径,且dist最小的顶点Vi,令final[i]=ture。
- 检查所有邻接自V的顶点,若其final值为false,则更新dist和 path 信息。
- 第2轮:循环遍历所有结点,找到还没确定最短路径,且dist最小的顶点Vi,令final[i]=ture。
- 检查所有邻接自V的顶点,若其final值为false,则更新dist和path 信息。
- 直到最后一轮:循环遍历所有结点,找到还没确定最短路径,且dist最小的顶点Vi,令final[i]=ture。
4.算法实现
- 初始:若从Vo开始,令final[0]=ture; dist[0]=O; path[0]=-1。
- 其余顶点final[k]=false;dist[k]=arcs[0][k]; path[k]= (arcs[O][k]==co) ? -1:0。
- n-1轮处理∶循环遍历所有顶点,找到还没确定最短路径,且dist最小的顶点V,令finali]=ture。并检查所有邻接自Vi的顶点,对于邻接自Vi的顶点V,若final[i]==false且dist[i]+arcs[i]i]< dist[i],则令dist[i]=dist[i]+arcs[i]lil; path[i]=i。(注: arcs[们]表示V到V%的弧的权值)
某个结点到其他结点的最短路径的时间复杂度为O(N2)即O(|V|2),
也可用Dijkstra算法求所有顶点间的最短路径,重复V次即可,总的时间复杂度也是OIV|3).
5.用于带负权值带权图
结论:Dijkstra算法不适用于有负权值的带权图。
2.各顶点间的最短路径
1.Floyd算法(带权图、无权图)
Floyd算法:求出每一对顶点之间的最短路径。
1.算法思想
使用动态规划思想,将问题的求解分为多个阶段:
- 对于n个顶点的图G,求任意一对顶点Vi->Vj之间的最短路径可分为如下几个阶段:#初始︰不允许在其他顶点中转,最短路径是?
- #O:若允许在Vo中转,最短路径是?
- #1∶若允许在Vo、V中转,最短路径是?
- #2:若允许在Vo、V1、V2中转,最短路径是?
- #n-1:若允许在Vo、V1、V2… Vn-1中转,最短路径是?
2.算法实现
- 定义一个二维数组A(相当于图的邻接矩阵)存储每个顶点之间的最短路径
- 定义一个二维数组path存储A位置对应路径需要经过的中转顶点。
- 使用动态规划,逐渐增加可以中转顶点个数,更新两个二维数组的信息。
3 .代码实现
时间复杂度,O(IVl3)
空间复杂度,O(IV|2)
// ......准备工作,根据图的信息初始化矩阵A和path (如上图)for (int k = 0; k < n; k++) {//考虑以vk 作为中转点for (int i = 0; i < n; i++) {//遍历整个矩阵,i为行号,j为列号for (int j = 0; j < n; j++) {if (A[i][j] > A[i][k] + A[k][j]) {//以Vk 为中转点的路径更短A[i][j] = A[i][k] + A[k][j];//更新最短路径长度path[i][j] = k; //中转点}}}}
4.Floyd算法可以用于负值带权图
Floyd算法不能解决带有“负权回路”的图(有负权值的边组成回路),这种图有可能没有最短路径。
3.三种算法的比较
| BFS 算法 | Dijkstra算法 | Floyd 算法 | |
|---|---|---|---|
| 无权图 | √ | √ | √ |
| 带权图 | x | √ | √ |
| 带负权值的图 | x | x | x |
| 带负权回路的图 | x | x | x |
| 时间复杂度 | O(V2)或O(V+E) | O(V2) | O(V3 ) |
| 通常用于 | 求无权图的单源最短路径 | 求带权图的单源最短路径 | 求带权图中各顶点间的最短路径 |
相关文章:
)
图:最短路径问题(BFS算法,Dijkstra算法,Floyd算法)
1 .单源最短路径 1.BFS算法(无权图) 使用广度优先遍历实现一个顶点到达其他所有顶点的最短路径。 注:无权图可以视为一种特殊的带权图,只是每条边的权值都为1。 1.算法思路: 定义一个数组存储每个结点与当前的结点的最短距离,定义一个数组…...
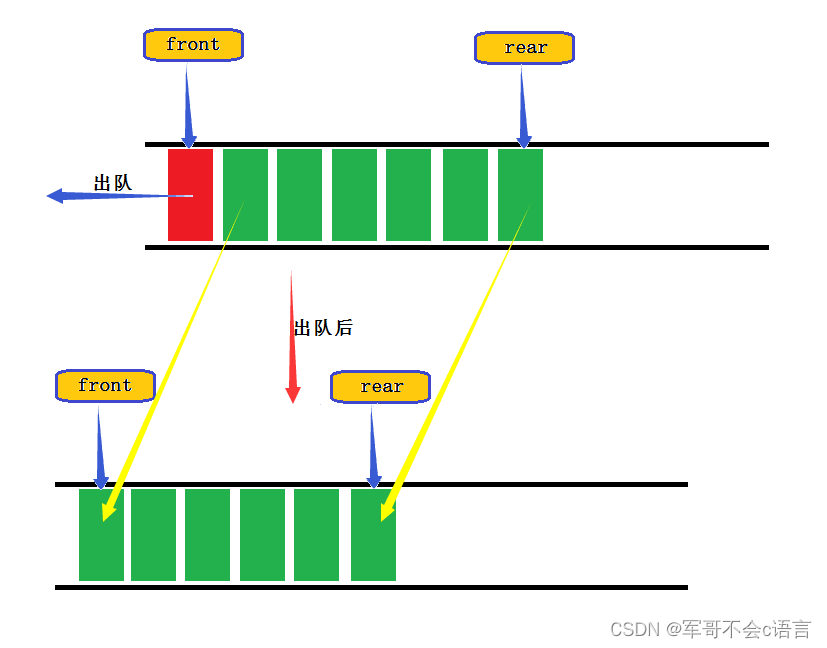
栈和队列篇
目录 一、栈 1.栈的概念及结构 1.1栈的概念 1.2栈的结构示意图 2.栈的实现 2.1支持动态增长的栈的结构 2.2压栈(入栈) 2.3出栈 2.4支持动态增长的栈的代码实现 二、队列 1.队列的概念及结构 1.1队列的概念 1.2队列的结构示意图 2.队列的实…...
分享一个vue-slot插槽使用场景
需求再现 <el-table-column align"center" label"状态" prop"mitStatus" show-overflow-tooltip />在这里,我想对于状态进行一个三目判断,如果为0那就是进行中,否则就是已完成,期初我是这样写…...
Qt应用开发(基础篇)——进度对话框 QProgressDialog
一、前言 QProgressDialog类继承于QDialog,是Qt设计用来反馈进度的对话框。 对话框QDialog QProgressDialog提供了一个进度条,表示当前程序的某操作的执行进度,让用户知道操作依旧在激活状态,配合按钮,用户就可以随时终…...

基于SpringBoot2的后台业务管理系统
概述 SpringBoot-Plus 是一个适合大系统拆分成小系统的架构,java快速开发平台,或者是一个微服务系统。其中加入了Thymeleaf数据模板语言代替了之前的JSP页面方式。页面展示采用Layui前端框架,包含了用户管理,角色管理,…...
Jmeter(三十):并发测试(设置集合点)
集合点:让所有请求在不满足条件的时候处于等待状态。 如:我集合点设置为50,那么不满足50个请求的时候,这些请求都会集合在一起,处于等待状态,当达到50的时候,就一起执行。从而达到并发的效果。 那么Jmeter中可以通过同步定时器 Synchronizing Timer 来完成。 Number …...
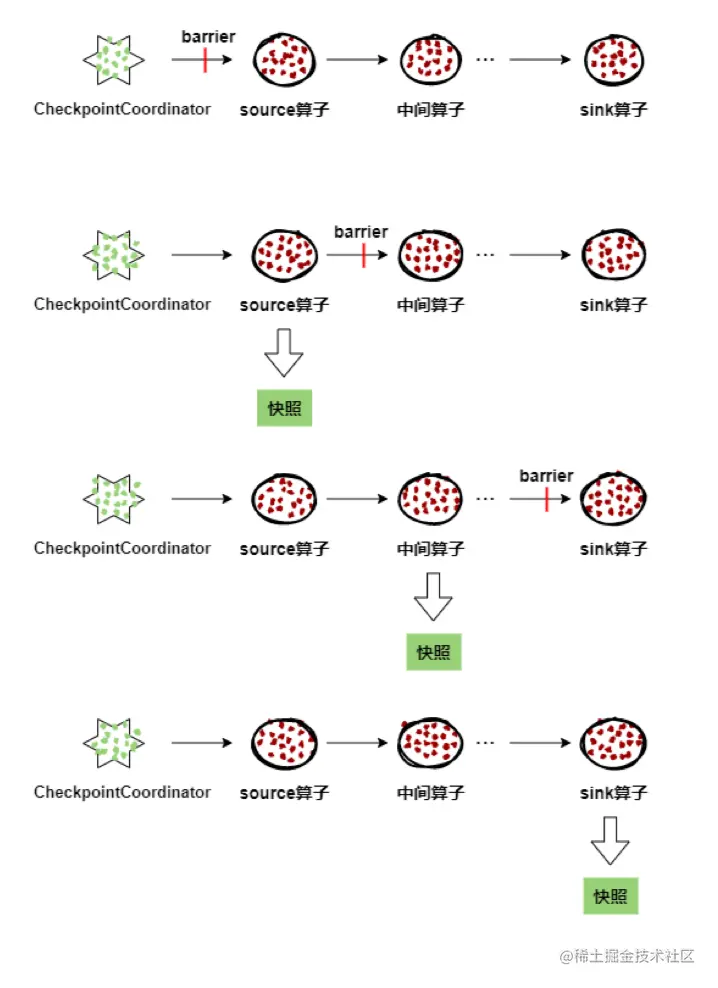
Flink的checkpoint是怎么实现的?
分析&回答 Checkpoint介绍 Checkpoint容错机制是Flink可靠性的基石,可以保证Flink集群在某个算子因为某些原因(如 异常退出)出现故障时,能够将整个应用流图的状态恢复到故障之前的某一状态,保证应用流图状态的一致性。Flink的Checkpoint机制原理来自“Chandy-Lamport alg…...

ubuntu上安装nginx
这篇文章主要介绍怎么在ubuntu上安装nginx服务器,并进行一些简单的配置。 第一步:准备好一台ubuntu操作系统的虚拟机 注意:如果你还没有安装好ubuntu,个人推荐阅读以下文章完成unbutu安装,vm的版本不用刻意安装文章中…...

9. 微积分 - 导数
文章目录 导数求导实例代码演示:迭代法求解二次函数最小值阶Hi, 大家好。我是茶桁。 我们终于结束了极限和连续的折磨,开启了新的篇章。 不过不要以为我们后面的就会很容易,只是相对来说, 没有那么绕而已。 那么,我们今天开始学习「导数」。 导数 在之前的导论,也就是…...

滑动窗口系列1-达标子数组
#达标子数组# 求达标子数组的数量 * 题目:给定一个数组,求满足子数组中最大值-最小值小于等于某个数的子数组的数量 * 例如[0,1,2,3]中求子数组中最大值-最小值小于等于 2的子数组的数量 * 结果为9,因为满足条件的只有[0,0] [0,1] [0,2] [1,1] [1,2] [1…...
)
电视显示技术及价格成本对比(2023年)
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 本文链接:https://blog.csdn.net/zaibeijixing/article/details/132461068 ———————————————— 截止到2023年ÿ…...

浅谈 Pytest+HttpRunner 如何展开接口测试!
软件测试有多种多样的方法和技术,可以从不同角度对它们进行分类。其中,根据软件生命周期,针对不同的测试对象与目标,可将测试过程分为 4 个阶段:单元测试、集成测试、系统测试和验收测试。本文着重介绍了如何借用 pyte…...
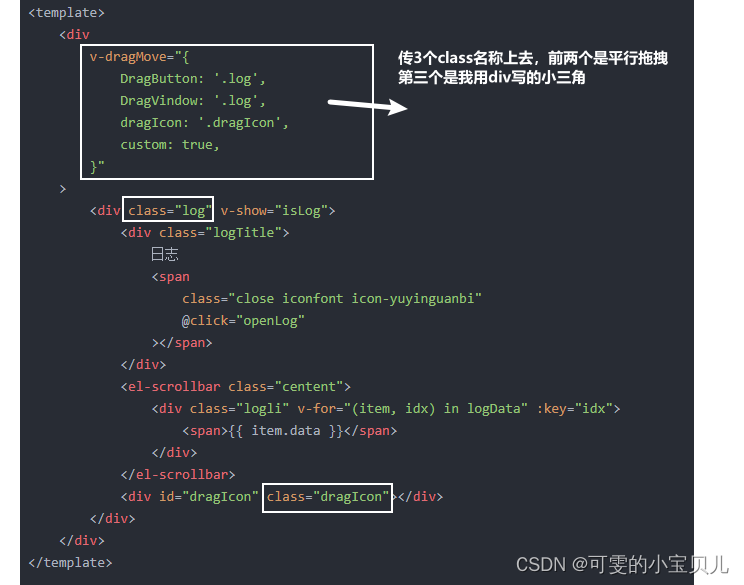
vue自定义事件 div 拖拽方法缩小
在main.js 引用 // 引入拖动js import dragMove from "./utils/dragMove.js" 创建 drawmove.js export default (app) > {app.directive(dragMove, (el, binding) > {const DragVindow el.querySelector(binding.value.DragVindow)// 按下鼠标处理事件con…...

使用实体解析和图形神经网络进行欺诈检测
图形神经网络的表示形式(作者使用必应图像创建器生成的图像) 一、说明 对于金融、电子商务和其他相关行业来说,在线欺诈是一个日益严重的问题。为了应对这种威胁,组织使用基于机器学习和行为分析的欺诈检测机制。这些技术能够实时…...

vue中axios请求篇
vue中如何发起请求? 利用axios来发起请求,但是前期需要配置 首先安装axios 可以使用npm、yarn等进行安装 npm安装方式 npm install axios -sava //在项目文件夹中打开cmd或者终端进行安装依赖 yarn安装方式 yarn add axios 引入axios。我一般是在src下创建一个u…...
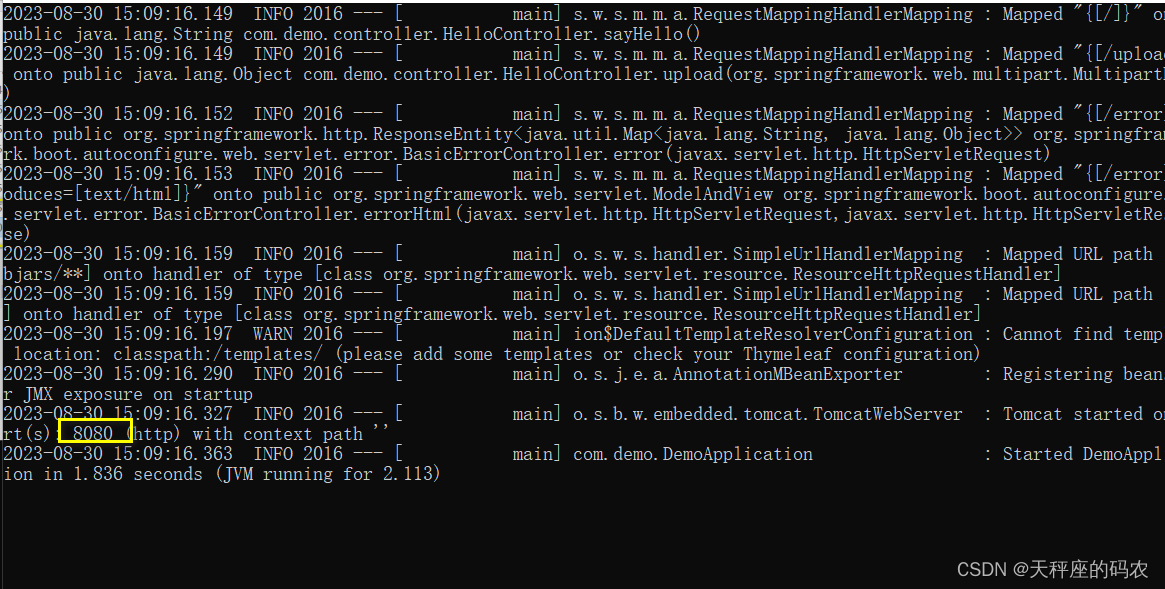
Springboot2.0 上传图片 jar包导出启动(第二章)
目录 一,目录文件结构讲解二,文件上传实战三,jar包方式运行web项目的文件上传和访问处理(核心知识)最后 一,目录文件结构讲解 简介:讲解SpringBoot目录文件结构和官方推荐的目录规范 1、目录讲解…...
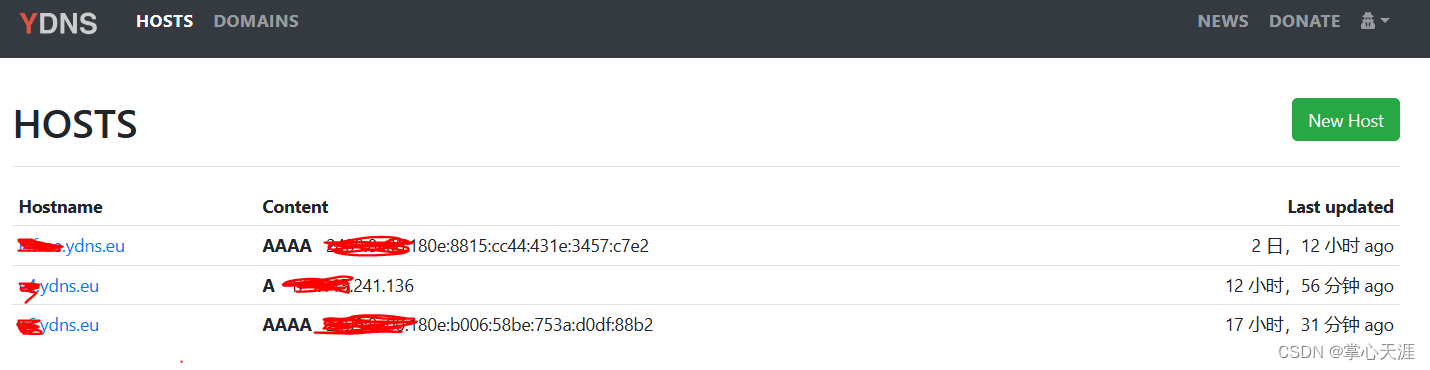
添加YDNS免费的ipv6动态域名解析
背景 又到了一年一度的dns域名到期,寻找替代了,前几年用了阿里、华为的免费域名,支持了几个搭建在NAS上的微服务;一旦涉及到域名续费,价格就比首年上去了不少,所以,打算找个长期的免费域名。 搜…...

爬虫异常处理之如何处理连接丢失和数据存储异常
在爬虫开发过程中,我们可能会遇到各种异常情况,如连接丢失、数据存储异常等。本文将介绍如何处理这些异常,并提供具体的解决代码。我们将以Python语言为例,使用requests库进行网络请求和sqlite3库进行数据存储。 1. 处理连接丢失 …...
KVM虚拟化ubuntu
KVM(Kernel-based Virtual Machine)是一种基于Linux内核的虚拟化技术,它将Linux内核作为虚拟机的底层操作系统,利用硬件虚拟化支持创建和管理虚拟机。KVM虚拟化技术被广泛应用于云计算、虚拟化服务器、虚拟化桌面等场景。 KVM虚拟…...
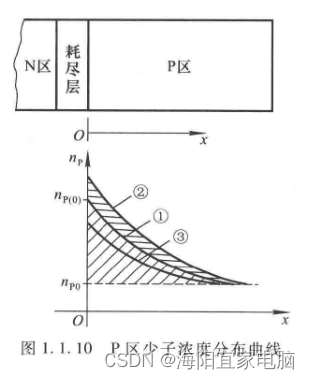
模拟电子技术基础学习笔记三 PN结
采用不周的掺杂工艺,将P型半导体与N型半导体制作在同一块硅片上,在它们的交界面就形成PN结。 扩散运动 物质总是从浓度高的地方向浓度低的地方运动,这种由于浓度差而产生的运动称为扩散运动。 空间电荷区 - 耗尽层 漂移运动 在电场力的作…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
