数据结构与算法系列之kmp算法

什么是kmp算法
1.kmp算法是一种改进的字符串算法,其核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数已达到快速匹配的目的。
它主要实现作用的是 在 (主串)中找到 (匹配)字符串。
例
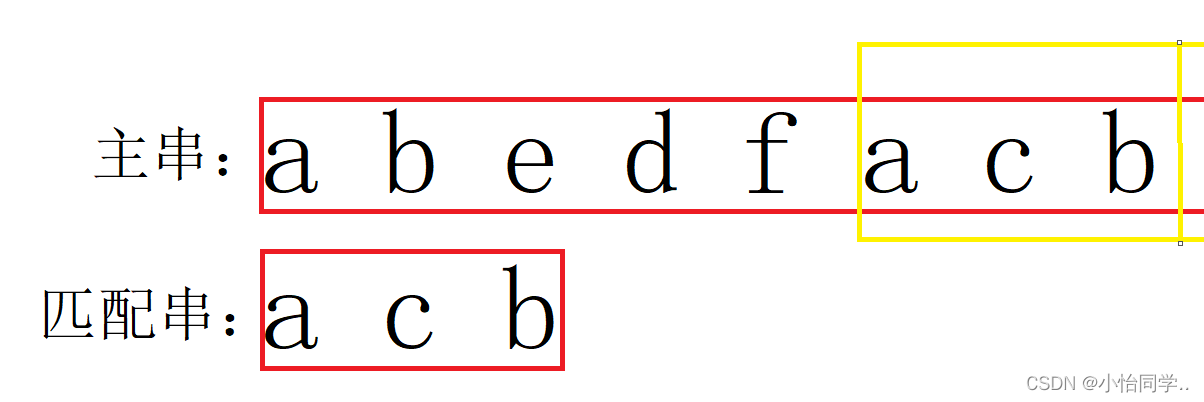
BF算法与kmp算法的差别
bf算法如下所示 从首元素字符开始依次比较 ,如果相同则比较下一位元素,如果匹配失败 ,匹配字符串从头开始 ,主串从第二个字符开始比较,直到主字符串全部匹配完。如果匹配成功返回主字符串中第一次出现匹配字符串的位置。
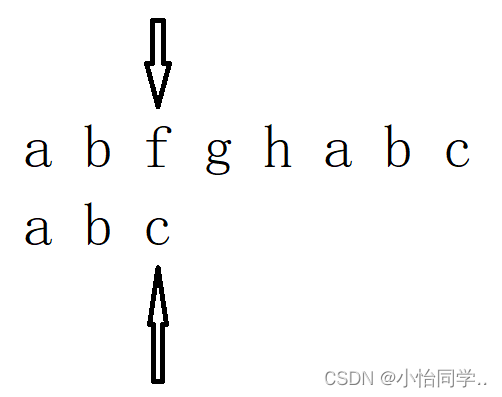

kmp算法如下所示,kmp与bf不一样的地方在于:主串的所指向的字符不会后退,匹配串中所指向的也不会移动到首字符位置
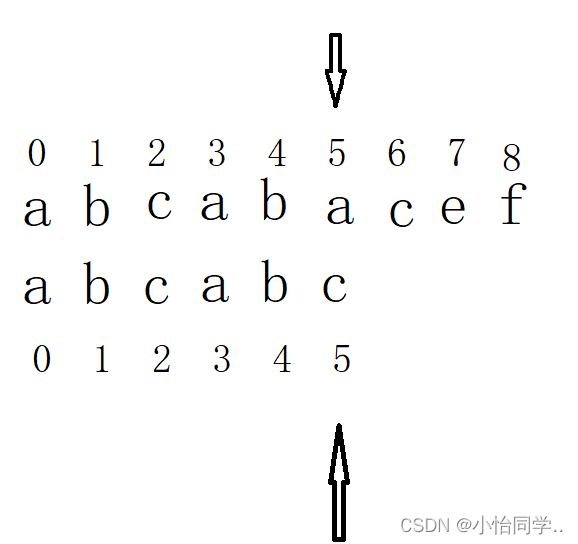
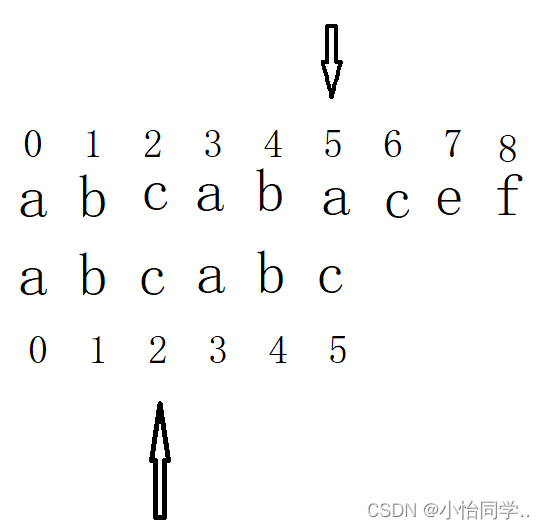
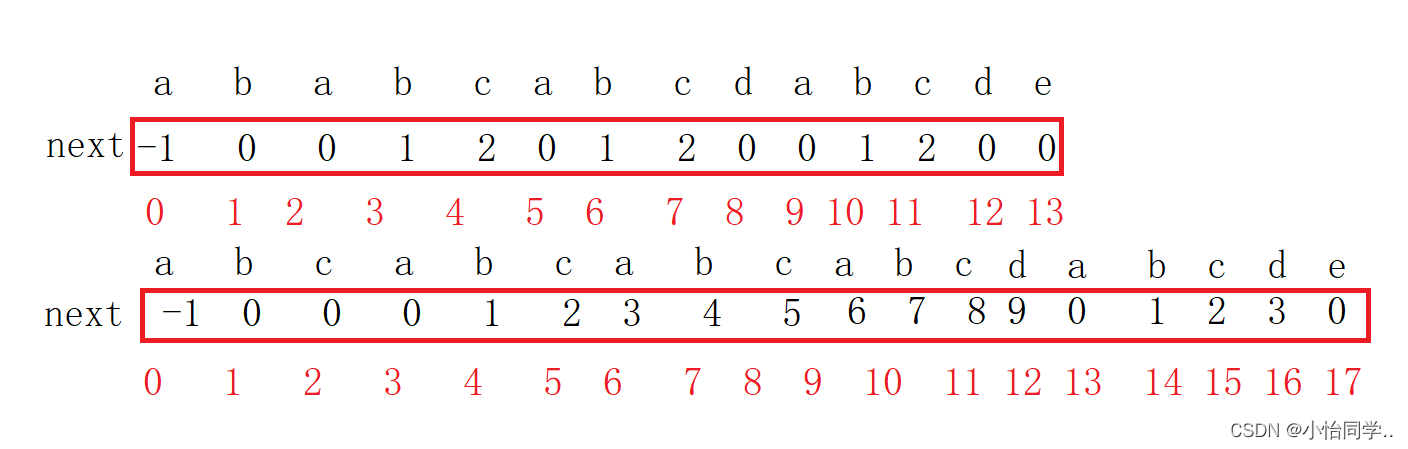
kmp的回退规则,next数组的介绍
目的是使 指向主串字符不会回退 ,匹配串回退到一个特定位置






这就是next数组的来源
规定next[0]=-1 next[1]=0
回退前提 : p[i] == p[k] 则 p[i] == p[k] next[i+1] == k+1 ,如果 p[i] != p[k] 则 next[k] != k, k==next[k] ,一直回退直到p[i] == p[k]
p[i] == p[k] 如下
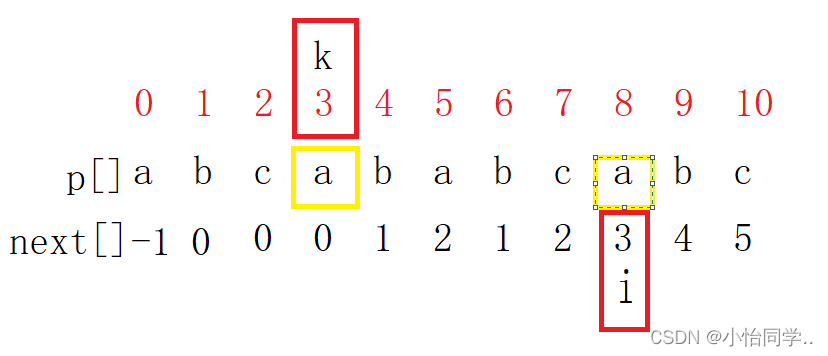
p[i] != p[k]如下
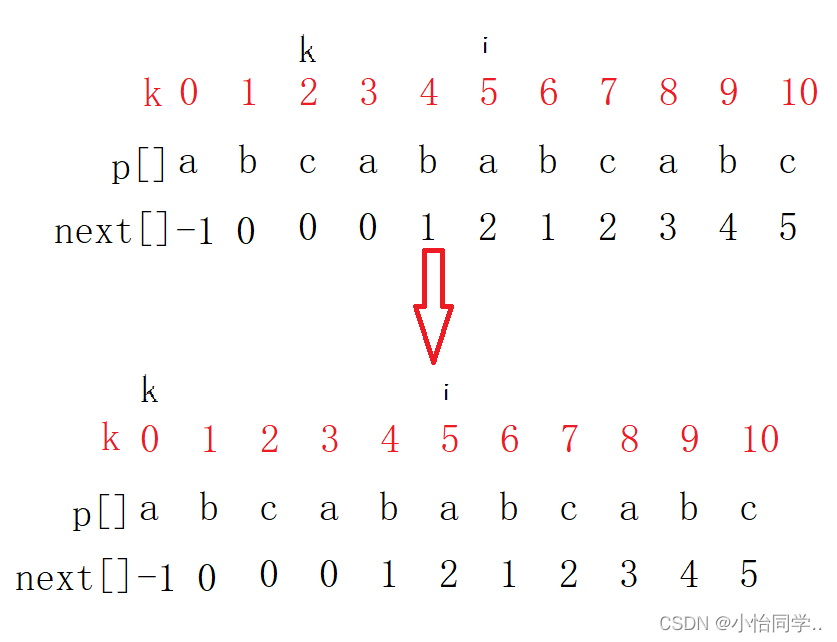
kmp算法代码实现(C语言版)
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <string.h>
void GetNext(char*sub, int* next ,int LenSub)
{next[0] = -1;next[1] = 0;int k = 0;int i = 2;while(i < LenSub){if (k == -1 || sub[i - 1] == sub[k]){next[i] = k + 1;i++;k++;}else{k = next[k];}}
}
int KMP(char* str, char* sub, int pos)
{assert(str && sub );int LenStr = strlen(str);int LenSub = strlen(sub);if (LenStr == 0 || LenSub == 0)return -1;if (pos < 0 || pos >= LenStr)return -1;int* next = (int*)malloc(sizeof(int) * LenSub);assert(next);GetNext(sub, next,LenSub);int i = pos;//主串int j = 0;//字串while (i < LenStr && j < LenSub){if (j == -1 || str[i] == sub[j]){i++;j++;}else{j = next[j];}}if (j >= LenSub)return i - j;return -1;
}int main()
{printf("%d", KMP("ababcabcdabcde", "abcd", 0));return 0;
}

相关文章:

数据结构与算法系列之kmp算法
什么是kmp算法 1.kmp算法是一种改进的字符串算法,其核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数已达到快速匹配的目的。 它主要实现作用的是 在 (主串)中找到 (匹配)字符串。 例 BF算法与k…...

算法分析详解
自古老的公元前1世纪开始,《周髀算经》就作为中国最古老的天文学和数学著作。 《周髀算经》采用最简便可行的方法确定天文历法,揭示日月星辰的运行规律,包括四季更替,气候变化,南北有极,昼夜相推的道理。为…...

东南大学自然辩证法概论期末总结
写在前面 作者:夏日 博客地址:https://blog.csdn.net/zss192 本文为2022年东南大学自然辩证法概论期末总结,内容为根据老师所发题纲综合多个资料总结得来 考试形式:从老师所发题纲,10个题目中选出4个,题…...

《爆肝整理》保姆级系列教程python接口自动化(二十)--token登录(详解)
简介 为了验证用户登录情况以及减轻服务器的压力,减少频繁的查询数据库,使服务器更加健壮。有些登录不是用 cookie 来验证的,是用 token 参数来判断是否登录。token 传参有两种一种是放在请求头里,本质上是跟 cookie 是一样的&…...
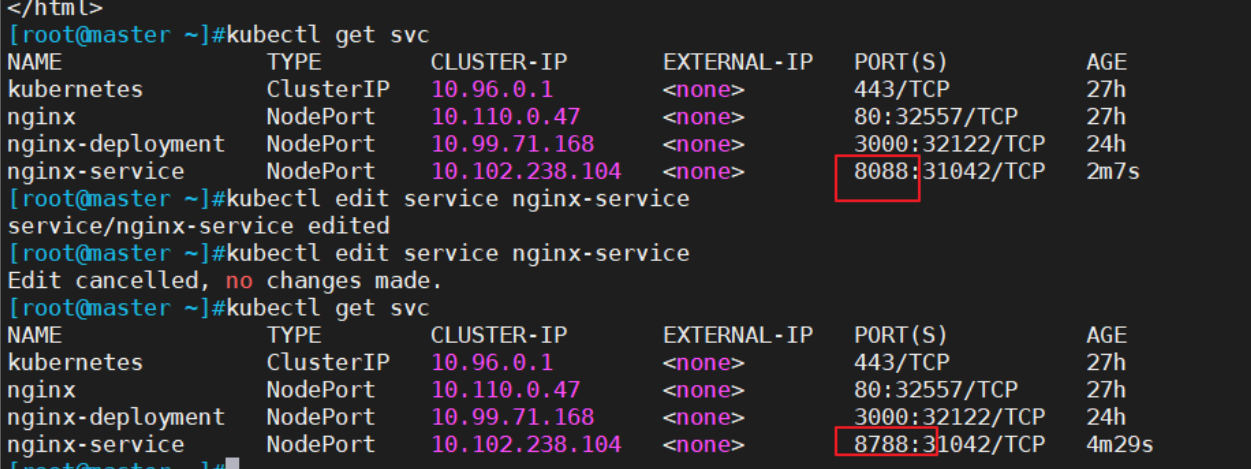
k8s种的kubectl命令
一.kubectl基本命令1.1 称述式资源管理的方法kubernetes集群管理集群资源的唯一入口是通过相应的方法调用apiserver的接口kubectl是官方的CLI命令行工具,用于与apiserver进行通信,将用户在命令行输入的命令,组织并转化为apiserver能识别的信息…...

数组(一)-- LeetCode[26][80] 删除有序数组中的重复元素
1 删除有序数组中的重复项 1.1 题目描述 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。 由于在某些语言中不能改变数组的长度,…...
GEE学习笔记 六十三:新的地图图层ui.Map.CloudStorageLayer
在GEE中导出数据有一种方式是直接导出地图到Google Cloud Storage中,也就是Export.map.toCloudStorage(xxx),这种方式是将我们计算生成影像导出成为静态瓦片的格式存放在Google Cloud Storage中。我们可以在其他的前端程序比如OpenLayer、Mapbox GL JS等…...

ClickHouse 语法详解
ClickHouse有2类解析器:完整SQL解析器(递归式解析器),以及数据格式解析器(快速流式解析器) 除了 INSERT 查询,其它情况下仅使用完整SQL解析器。 INSERT查询会同时使用2种解析器:INSE…...
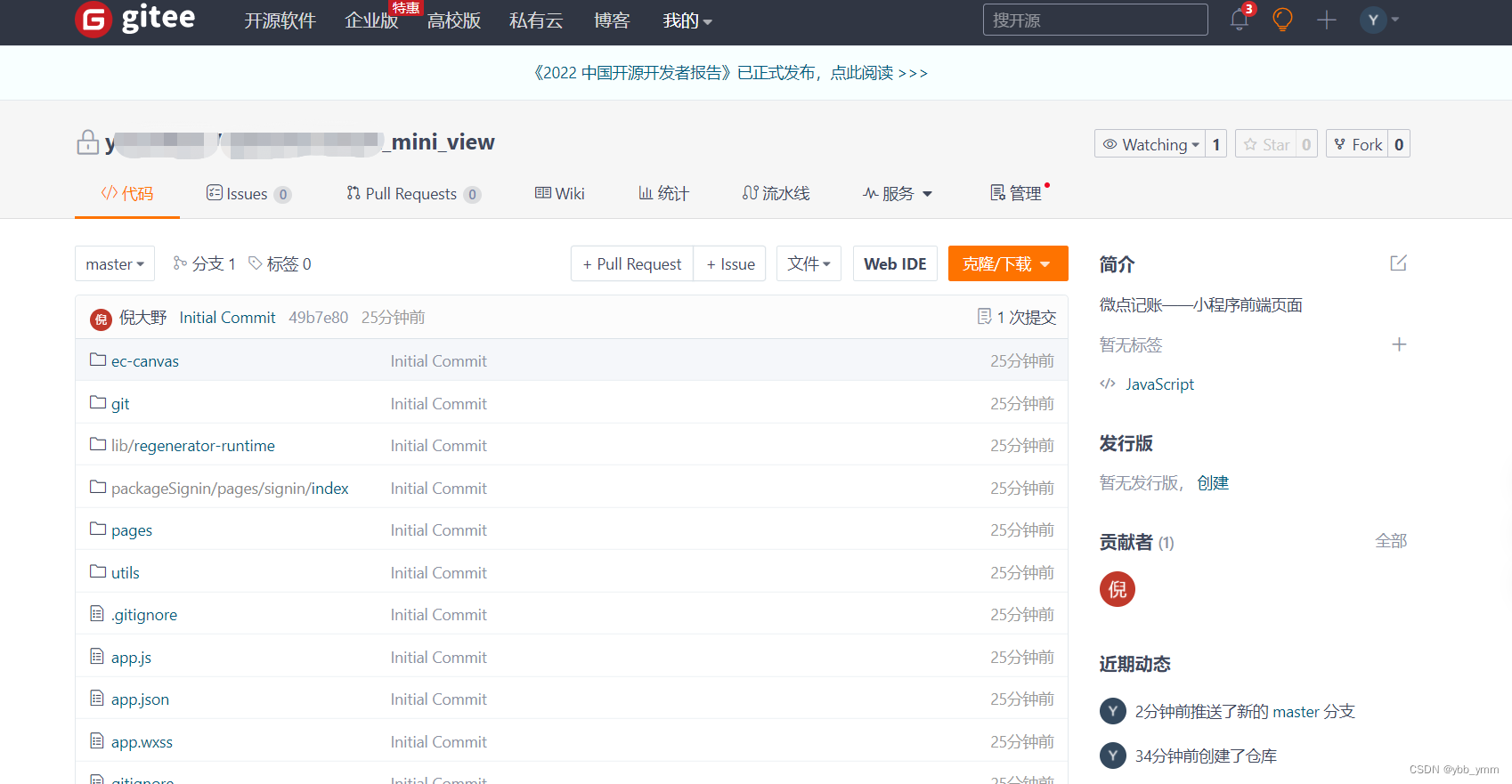
手把手教你将微信小程序放到git上
背景 首先,要创建一个自己的git仓库,这里默认大家都能够自己创建了git仓库了。如果不会创建仓库的话,百度一下,很容易就能够创建了!(后续,如有不知道在哪里,怎么创建仓库的话&#…...

功能测试3年,回顾一路走来的艰辛
不论你是什么时候开始接触测试这个行业的,你首先听说的应该是功能测试。通过一些测试手段来验证开发做出的代码是否符合产品的需求?当然你也有自己对功能测试的理解,但是最近两年感觉功能测试好像不太受欢迎,同时不少同学真的是功…...

作为Linux C/C++程序员必备的工具
Linux系统 可以选择centOS或者ubautu server(不建议选择桌面版本的)。不建议裸机安装,玩坏了就特别麻烦。不建议使用有桌面版本的ubautu,在一定程度有桌面的版本的会消耗性能。 如果经济实力允许,可以购买云服务器。 参考文章: Ubuntu server…...

docker Alpine一个只有5M小而美的Docker镜像
docker Alpine一个只有5M小而美的Docker镜像 参考链接: Alpine 一个只有5M的Docker镜像 http://www.infoq.com/cn/news/2016/01/Alpine-Linux-5M-Docker?utm_sourcetuicool&utm_mediumreferral 使用alpinelinux 构建 golang http 启动了才15mb http://blog.csdn.net/fre…...
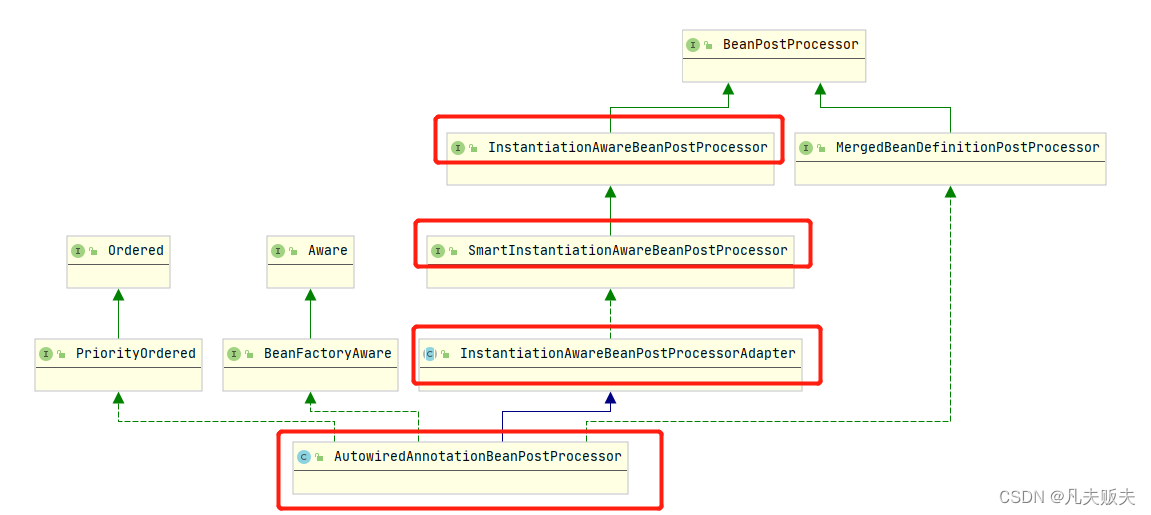
Springboot扩展点之InstantiationAwareBeanPostProcessor
Springboot扩展点系列实现方式、工作原理集合:Springboot扩展点之ApplicationContextInitializerSpringboot扩展点之BeanFactoryPostProcessorSpringboot扩展点之BeanDefinitionRegistryPostProcessorSpringboot扩展点之BeanPostProcessorSpringboot扩展点之Instant…...
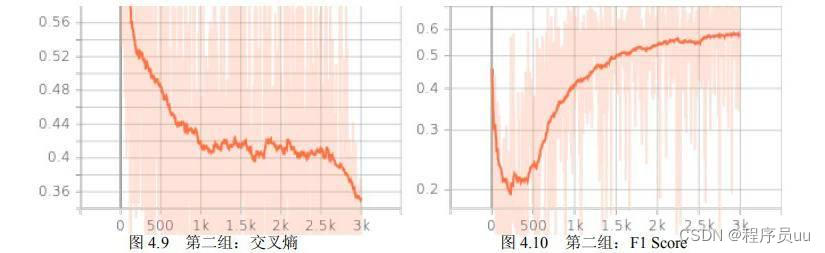
基于 U-Net 网络的遥感图像语义分割 完整代码+论文
一、研究目的U-Net 是一种由全卷积神经网络启发的对称结构网络,在医疗影像分割领域取得了很好的效果。 此次研究尝试使用 U-Net 网络在对多光谱遥感影像数据集上进行训练,尝试使用卷积神经网络自动分割出建筑,希望能够得到一种自动分割遥感影…...

Codeql 编译Shiro1.2.4爬坑
0x00 前言 这个Codeql一定要编译才能生成Database,是真的比较恼火,很多项目都不一定可以生成,环境就是一个非常大的坑,为了防止以后,所以将shiro1.2.4编译过程进行记录。 0x01 正文 首先是需要下载到shiro1.2.4的源…...

新C++(9):谈谈,翻转那些事儿
"相信羁绊,相信微光,相信一切无常。"一、AVL树翻转那些事儿(1)什么是AVL树?在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。…...

Java深克隆的几种方式
目录 1、通过继承Cloneable接口,重写clone方法实现深克隆 2、通过序列化与反序列化的方式实现深克隆 3、第三方工具类实现深克隆,克隆对象需继承Serializable接口 3.1、Apache Commons Lang的SerializationUtils.clone方法 3.2、Gson工具类 3.3、F…...
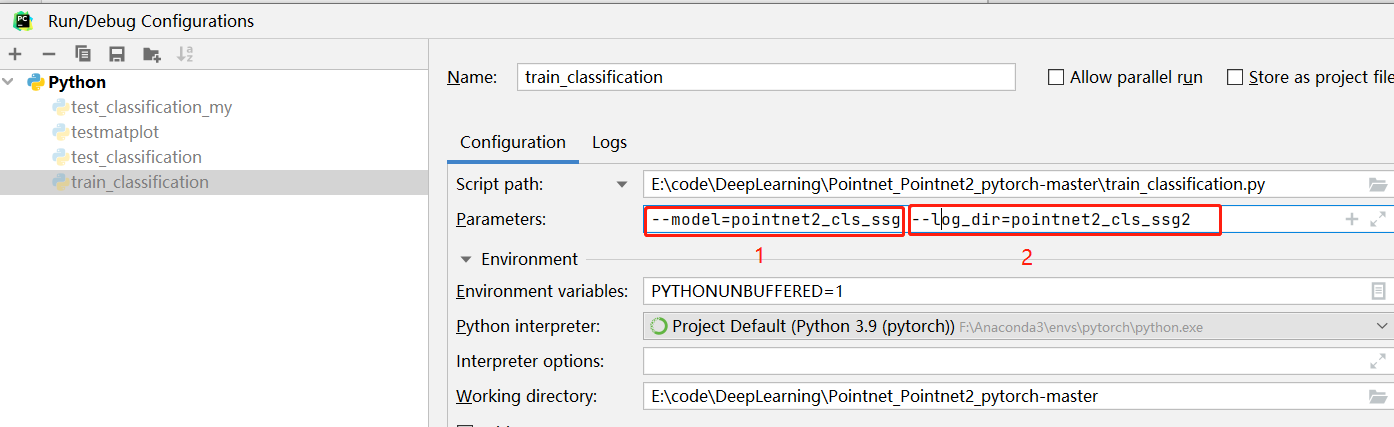
PointNet++的源码运行
首先,从github上下载源码https://github.com/yanx27/Pointnet_Pointnet2_pytorch也可以从百度网盘下载链接:https://pan.baidu.com/s/1sgTYuqnBVC9p3bib450SOQ 提取码:gujd再下载对应的测试数据分类数据modelnet40_normal_resampled下载&…...
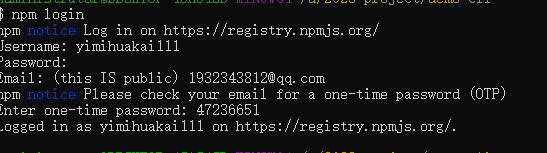
npm 上传自己的包
mkdir demo 创建一个新的文件夹 npm init 初始化项目 生成一个package.json文件 name version description等等touch index.js 创建一个node 可执行脚本新的js 文件 #!/usr/bin/env node // 必须在文件头加如上内容指定运行环境为node console.log(hello cli)在package.json 中…...

【Linux】常用命令大全(二)
目录 4. Linux常用命令 4.1 Linux命令初体验 4.2 文件目录操作命令 4.3 拷贝移动命令 4.4 打包压缩命令 4.5 文本编辑命令 4.6 查找命令 4. Linux常用命令 4.1 Linux命令初体验 4.1.1 常用命令演示 在这一部分中,我们主要介绍几个常用的命令,…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...