新C++(9):谈谈,翻转那些事儿

"相信羁绊,相信微光,相信一切无常。"
一、AVL树翻转那些事儿
(1)什么是AVL树?
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。而保证这颗树平衡的关键步骤,就是通过旋转来保证,由于增加、删除时对树的破坏的平衡。 取自这里
这样的树形结构,能够十分高效地查找"键值"(key/value模型)。C++中的STL容器,如map、set其底层就是由红黑树实现的。当然这是后半段会讲的一种优秀的数据结构。
AVL规则:
它的左右子树都是AVL树。
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)。
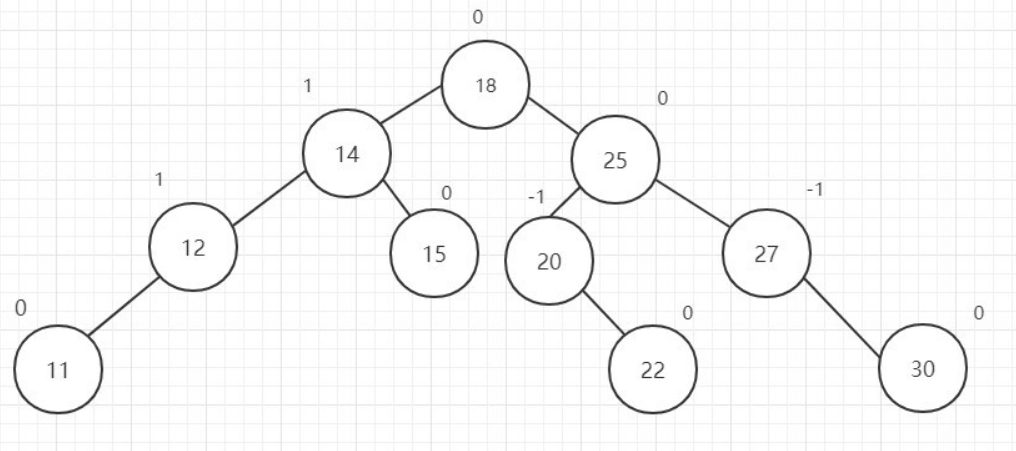
形如上图,每个节点的上标是该节点的左右子树的高度差。如果该AVL二叉树有N个节点,那么其高度可以保持LogN(以2为底),其搜索查找的时间复杂度为LogN(以2为底)。
(2)翻转那些事儿
条件检测;
上面的简介也说过,AVL树的平衡是通过旋转来维护的。那么什么时候需要翻转呢?什么时候不需要呢?我们在这里对每个节点引入 "平衡因子(bf)"的概念。对节点左右子树高度的检测,转移到了对平衡因子数值状态的检测。
root(当前节点) 我们对插入节点对平衡因子的更改做一个约定:左插入-- 右插入++。
① bf == 0时,说明当前左右子树高度平衡,不需要调整。
② bf == 1 || bf == -1时,说明这颗"root一定是从bf == 0变化而来的"。那么就不仅仅需要关注当前root节点平衡因子的变化,还需要"向上调整"。root = root->parent
③ bf == 2 || bf == -2 时,此时AVL条件树的已经不平衡了 需要手动翻转才能保证其平衡性。
单线旋转;
节点属性:
template<class K,class V>
struct AVLTreeNode
{std::pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;int _bf = 0;AVLTreeNode(const std::pair<K,V> kv):_kv(kv),_left(nullptr),_right(nullptr),_bf(0){}
};RotateR:
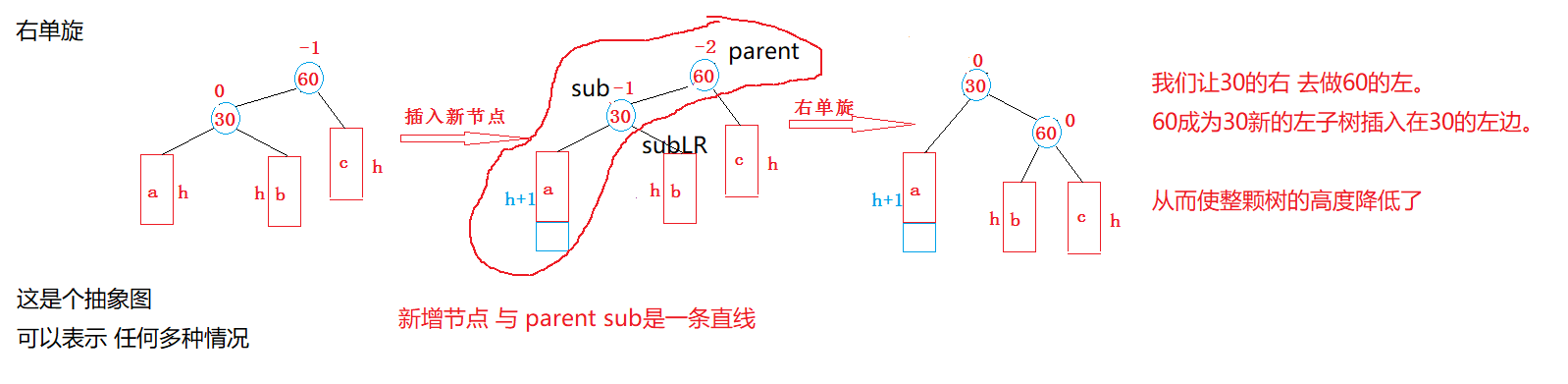
①让subLR作为左子树 连接在parent的左边。
②parent再作为subL的右子树连接。
③subL成为新的当前左右子树的根,并与上层parent->parent连接
void RotateL(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){//subLR 如果不为空才需要 连接parentsubLR->_parent = parent;}//连接诶父节点Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (root == nullptr){subL = root;subL->_parent == nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}//更新平衡因子subL->_bf = parent->_bf = 0;
}RotateL:
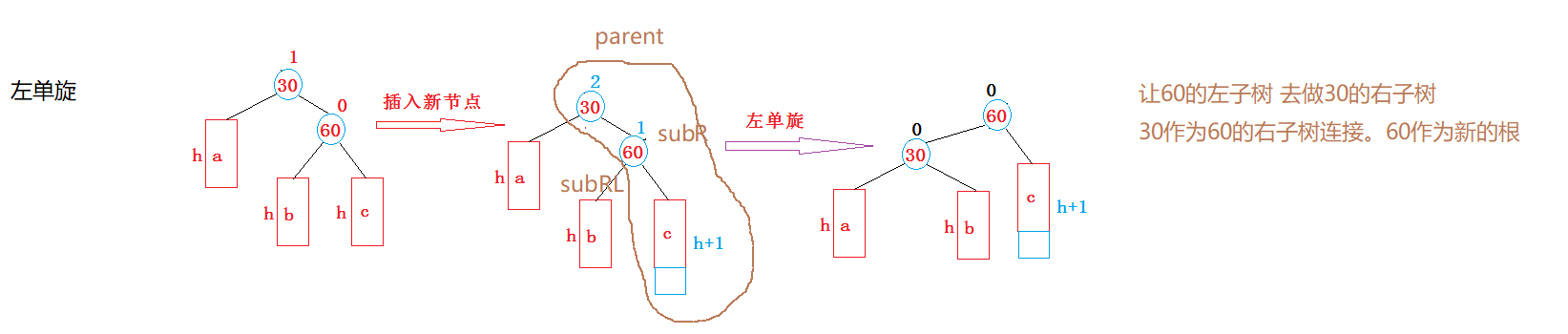
①让subRL作为30的右子树连接。
②parent作为subR的左子树连接。
③subR作为新的当前左右子树的根,并与上层parent->parent连接。
void RotateR(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subR;subR->_right = parent;if (root== nullptr){root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}subR->_bf = parent->_bf = 0;
}折线旋转;
其实单线旋转蛮简单的,并且旋转过后平衡因子都可以被直接处理为0。但是,如果是面对折线旋转的情况,仅仅考单旋处理,是不够的。
左右双旋:

右左双旋:
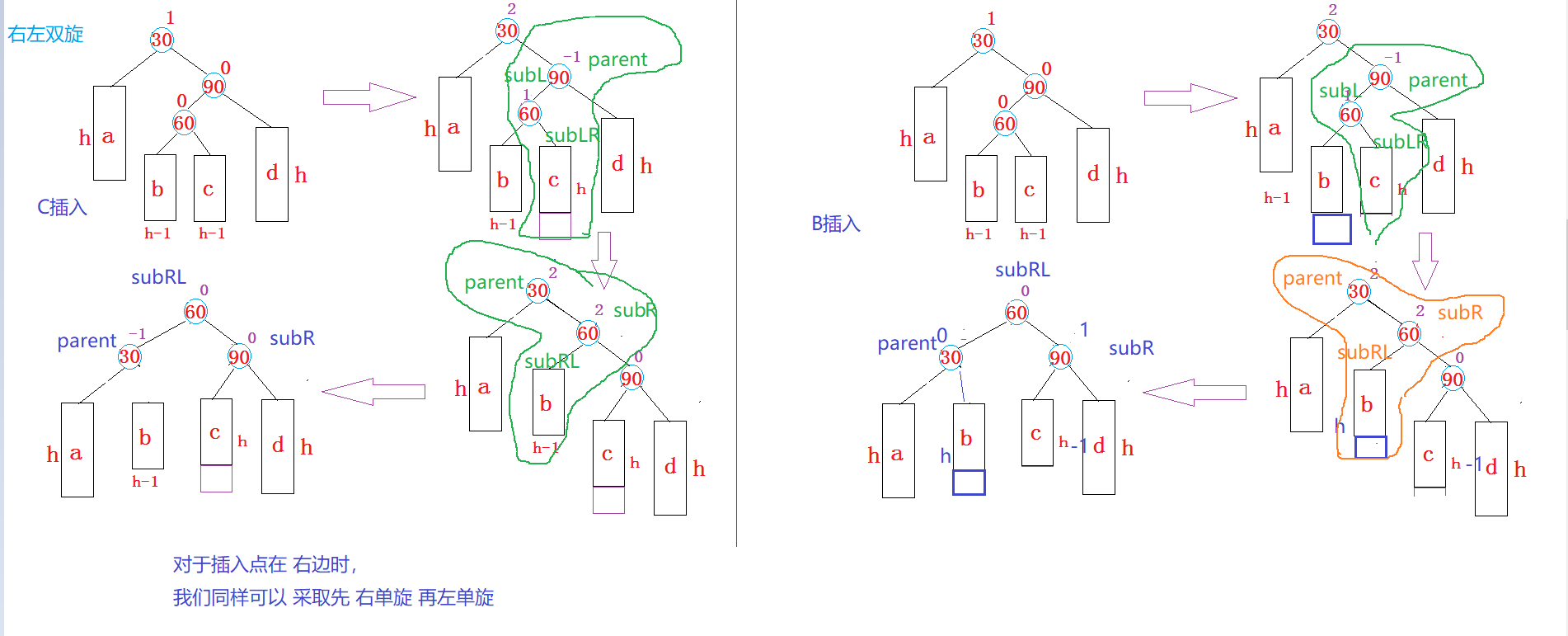
双旋的问题,我觉得难点不是在于旋转,因为前面已经解决了。而是如何处理双旋后的平衡因子与什么时候用双旋,什么时候用单旋?
单旋的判断很简单,因为是一条直线
即: (parent->bf == 2 && cur->bf == 1) || (parent->bf == -2 && cur->bf == -1)
双旋使用的场景,就是针对折线的插入节点
即: (parent->bf == 2 && cur->bf == -1) || (parent->bf == -2 && cur->bf == 1)
单旋情况下平衡因子的处理颇为简单易懂,一次翻转就可以将左右子树高度调平。
双旋情况下的平衡因子取决于subRL \ subLR 到底是左子树+1 还是右子树+1
对于右左双旋的情况,subRL的左子树会被parent去接手,反之subRL的右子树会被subL接手。
对于左右双旋的情况,subLR的左子树会被subR接手,而它的右子树会被parent接手。
其实还是一句话,画图才是王道。
void RotateRL(Node* parent)
{Node* subL = parent->_right;Node* subLR = subL->_left;//依据int bf = subLR->_bf;RotateR(subL);RotateL(parent);//说明是在cur的 左边插入if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == 1){//说明是在cur的 右边插入subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else{subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}
}void RotateLR(Node* parent)
{Node* subR = parent->_right;Node* subRL = parent->_left;int bf = subRL->_bf;RotateL(subR);RotateR(parent);if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else{subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}
}二、红黑树翻转那些事儿
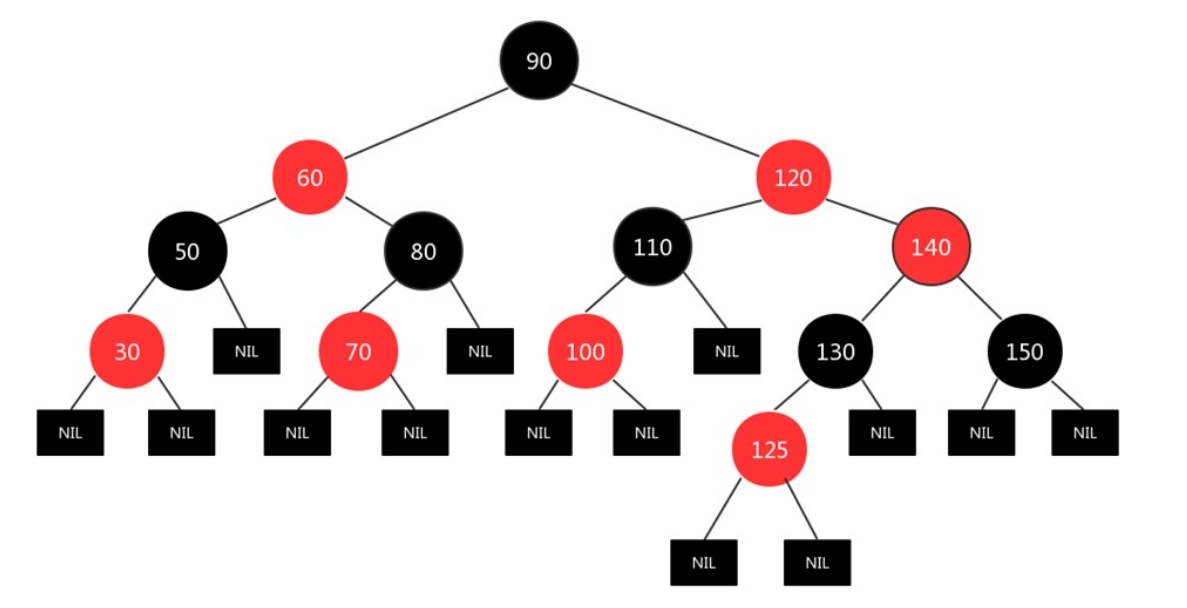
(1)什么是红黑树?
红黑树(Red Black Tree) 是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
为什么有了AVL树,又来了个红黑树呢?那必定红黑树一定有比起AVL树更加优势的地方。可以说,"AVL树是一位大佬设想,那么红黑树一定是出自一位天才的手笔。"
红黑树规则:
①每个结点不是红色就是黑色。
②根节点一定是黑色。
③不能出现连续的红色结点。
④对于每个结点到后代结点的简单路径上,都含有相同的黑色结点。
红黑树没有像AVL树那么严格地控制平衡(左右子树高度差不超过1),它是一种接近平衡的搜索二叉树。
红黑树规则的核心: 确保最长路径的结点数不超过最短路径节点数的2倍。
(2)翻转那些事儿
条件检测:
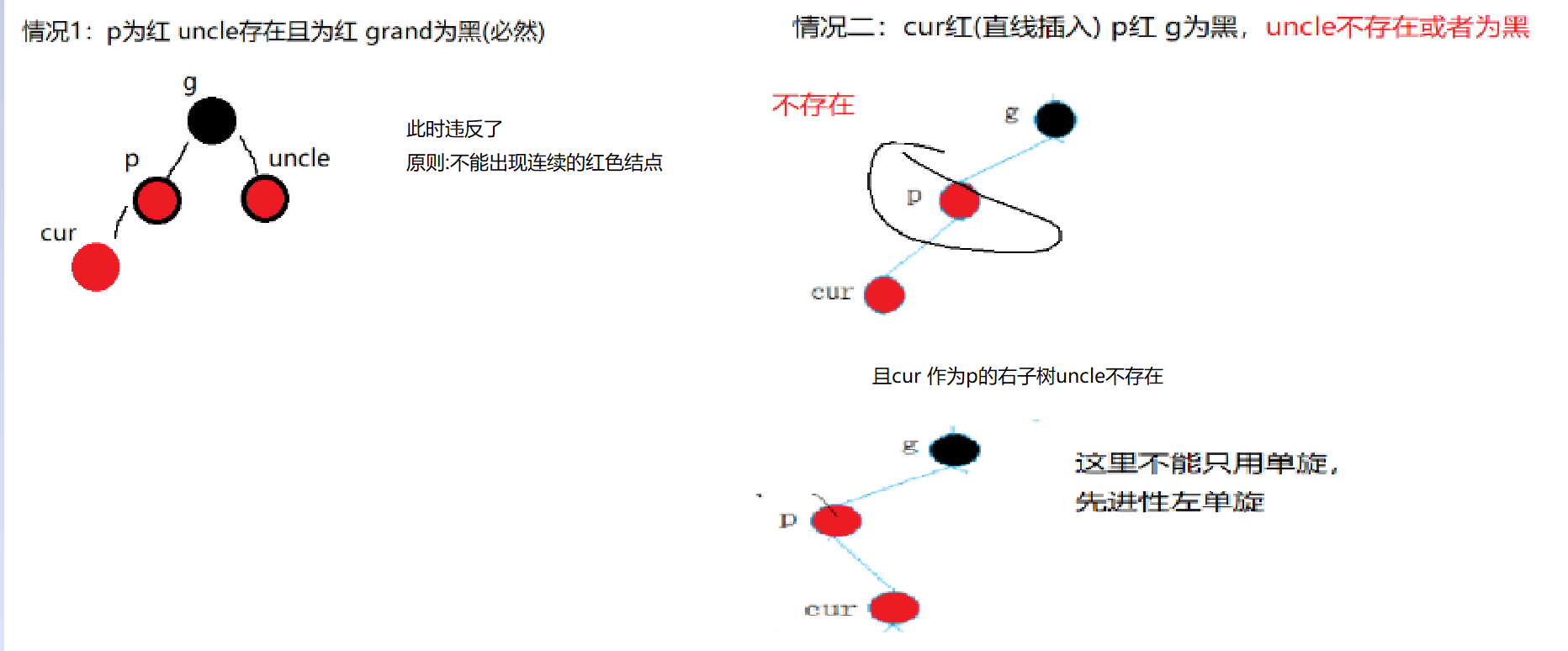
红黑树插入结点的情况,其实可以分为两大类:
①cur(新增结点)红 parent红 grandparent黑 uncle红
②cur(新增结点)红 paren红 grandparent黑 uncle不存在或者存在且为黑。
由此红黑树插入的关键为:uncle结点。
下面来看看这两种情况的对应图:
因为牵涉到翻转,正好我们也在AVL树那一小结写过,直接CV一份~
void RotateL(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode->_parent == nullptr){subL = root;subL->_parent == nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}
}void RotateR(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppNode = parent->_parent;parent->_parent = subR;subR->_right = parent;if (root== nullptr){root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}红黑树结点结构;
enum Color
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{std::pair<K, V> _kv;RBTreeNode<K, V>* _left = nullptr;RBTreeNode<K, V>* _right = nullptr;RBTreeNode<K, V>* _parent = nullptr;Color _color = RED;RBTreeNode(const std::pair<K, V>& kv):_kv(kv){}
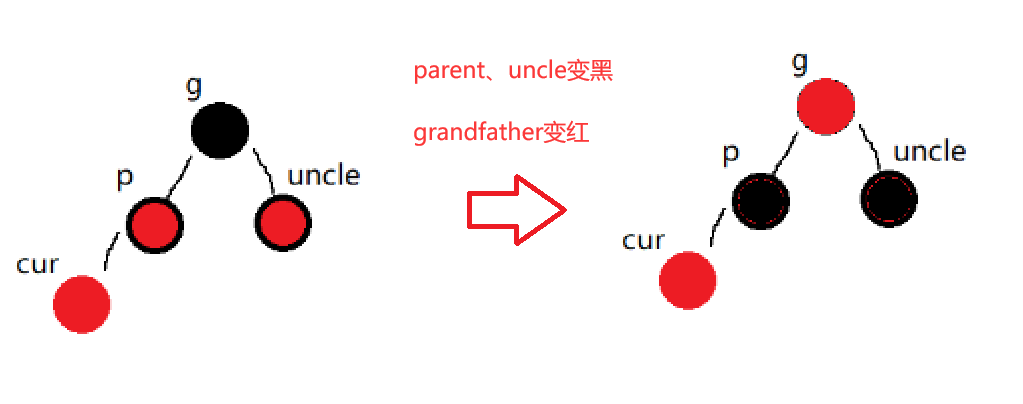
};uncle存在且为红:
我们让 parent 与 uncle同时变黑 并且 grandparent变为红色。
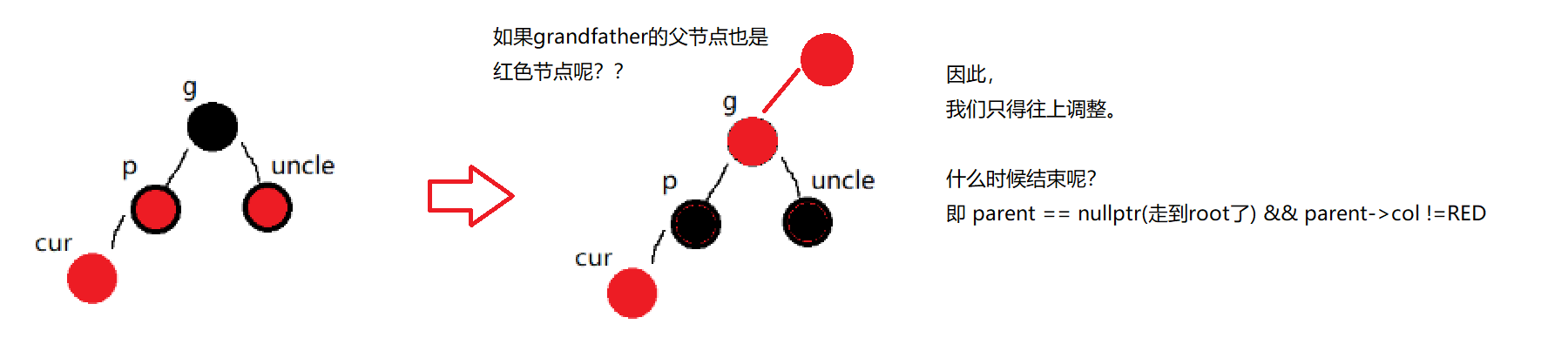
就结束了吗?当然不是!
bool Insert(const std::pair<K,V>& kv)
{//..Node* cur = new Node(kv);Node* parent = cur->_parent;while (parent &&parent->_color!= RED){Node* grandfather = parent->_parent;//找到uncle节点Node* uncle = nullptr;if (grandfather->_left == parent){uncle = grandfather->_right;//1.uncle存在且为红if (uncle && uncle->_color == RED){//着色uncle->_color = parent->_color = BLACK;grandfather->_color = RED;//继续向上调整cur = grandfather;parent = cur->_parent;}//......}else{uncle = grandfather->_left;//1.uncle存在且为红if (uncle && uncle->_color == RED){//着色uncle->_color = parent->_color = BLACK;grandfather->_color = RED;//继续调整cur = grandfather;parent = cur->_parent;}//......}}}uncle不存在或者uncle存在且为黑(cur为直线):

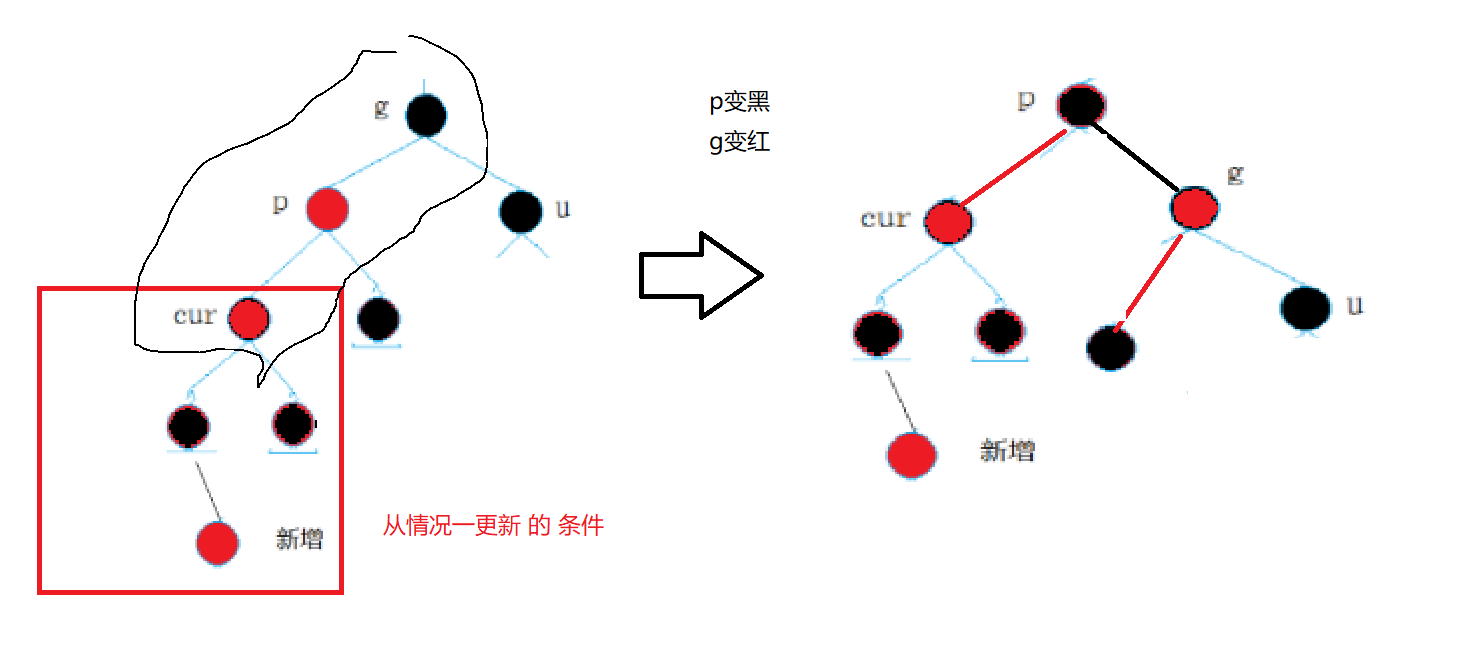
我们让parent变黑 grandfather变红
//uncle = grandfather->_right;
//uncle不存在或者存在且为黑
//parent在左 uncle在右 左子树
if (cur == parent->_left)
{RotateR(grandfather);//着色grandfather->_color = RED;parent->_color = BLACK;
}//uncle = grandfather->_left;
//uncle不存在或者存在且为黑
//parent在右 uncle在左 右子树
if (cur == parent->_right)
{RotateL(grandfather);grandfather->_color = RED;parent->_color = BLACK;
}uncle不存在或者uncle存在且为黑色(折线)
进一步复杂的情况,不单单是用单旋搞定。
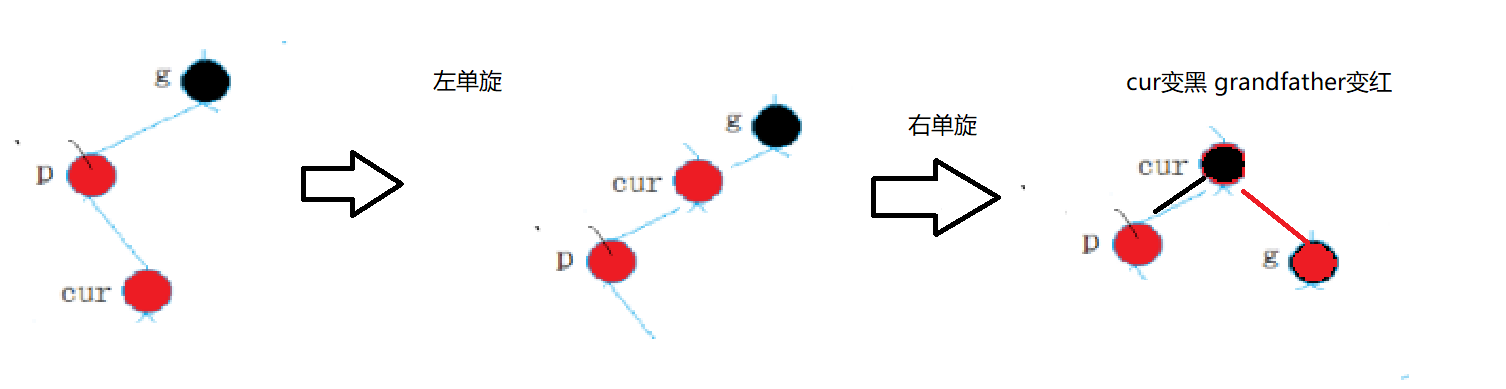
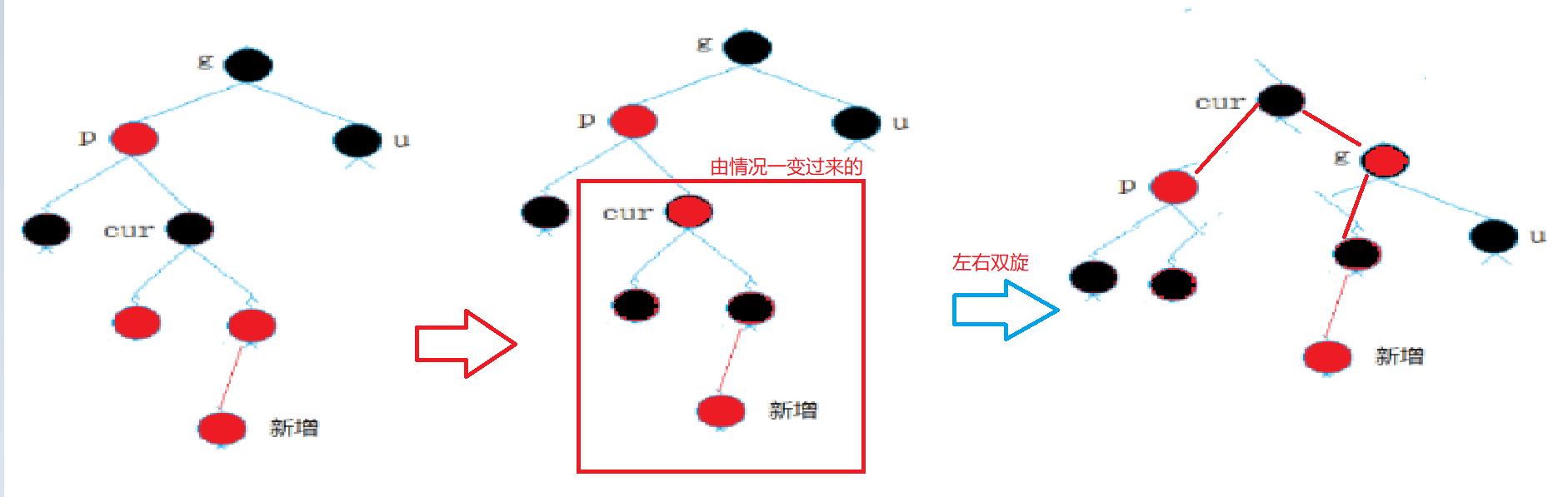
我们将cur变黑,grandfather变红
//uncle = grandfather->_right;
else{RotateL(parent);RotateR(grandfather);grandfather->_color = RED;cur->_color = BLACK;
}
//uncle = grandfather->_left;
//cur == parent->_left
else{RotateR(parent);RotateL(grandfather);grandfather->_color = RED;cur->_color = BLACK;
}总结:
AVL与红黑树都是搜索效率极其强悍的数据结构。红黑树不追求绝对的平衡,但是AVL却对左右子树的平衡关系严格要求。因此,对树的翻转次数一定多余红黑树。在插入时其性能效率也会相应受到影响。而且红黑树实现比较简单,所以实际运用中红黑树更多。
本篇到此为止,感谢你的阅读。
祝你好运,向阳而生~

相关文章:

新C++(9):谈谈,翻转那些事儿
"相信羁绊,相信微光,相信一切无常。"一、AVL树翻转那些事儿(1)什么是AVL树?在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。…...

Java深克隆的几种方式
目录 1、通过继承Cloneable接口,重写clone方法实现深克隆 2、通过序列化与反序列化的方式实现深克隆 3、第三方工具类实现深克隆,克隆对象需继承Serializable接口 3.1、Apache Commons Lang的SerializationUtils.clone方法 3.2、Gson工具类 3.3、F…...
PointNet++的源码运行
首先,从github上下载源码https://github.com/yanx27/Pointnet_Pointnet2_pytorch也可以从百度网盘下载链接:https://pan.baidu.com/s/1sgTYuqnBVC9p3bib450SOQ 提取码:gujd再下载对应的测试数据分类数据modelnet40_normal_resampled下载&…...
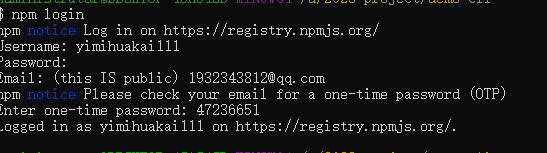
npm 上传自己的包
mkdir demo 创建一个新的文件夹 npm init 初始化项目 生成一个package.json文件 name version description等等touch index.js 创建一个node 可执行脚本新的js 文件 #!/usr/bin/env node // 必须在文件头加如上内容指定运行环境为node console.log(hello cli)在package.json 中…...

【Linux】常用命令大全(二)
目录 4. Linux常用命令 4.1 Linux命令初体验 4.2 文件目录操作命令 4.3 拷贝移动命令 4.4 打包压缩命令 4.5 文本编辑命令 4.6 查找命令 4. Linux常用命令 4.1 Linux命令初体验 4.1.1 常用命令演示 在这一部分中,我们主要介绍几个常用的命令,…...
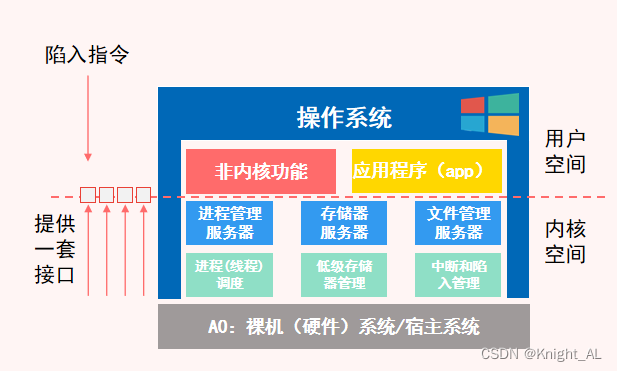
第一章 操作系统概述
目录一、什么是操作系统?1、操作系统的概念2、计算系统的构成3、主要作用二、操作系统有哪些功能?1、操作系统的目标2、操作系统的功能三、操作系统有哪些特征?1、并发性2、共享性3、虚拟性4、异步性四、操作系统的运行机制是怎样的ÿ…...
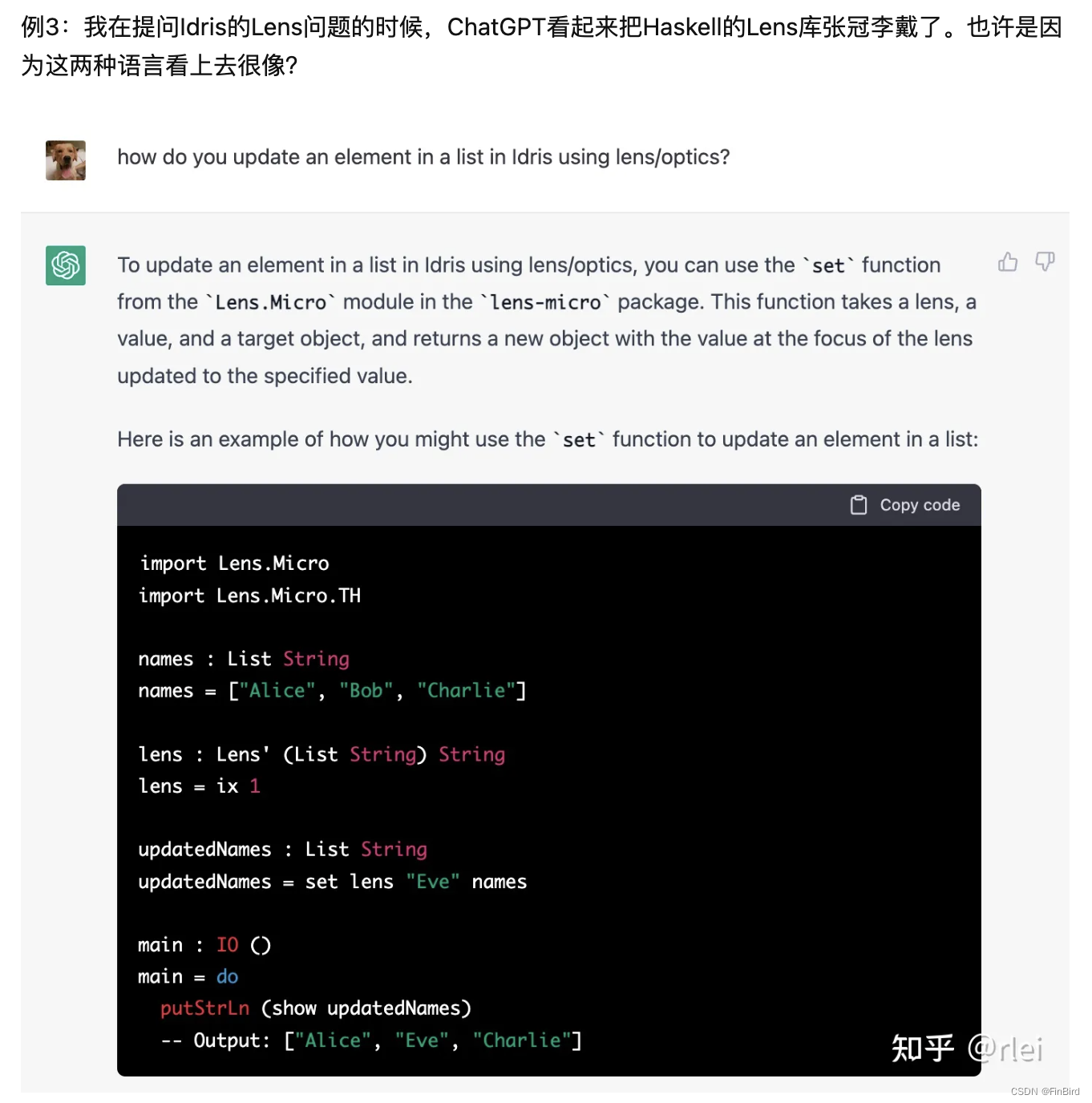
ChatGPT为什么不受开发者喜欢?
记得 ChatGPT 最开始上线不久的时候,看到的大部分尝鲜和测试结果都是开发者在做进行敲代码测试,可以说职业危机感非常强的一群人了。 再者,加上 ChatGPT 要使用起来其实是有一些技术门槛的,愿意折腾的人也多是程序员,…...

Lua table
Table(表) table 是 lua 中唯一的数据结构,可以用于表示 数组,字典与结构体。它非常强大,可以储存任何数据类型。 table 的数据单元为一对键值。 table 是不固定大小的,你可以根据自己需要进行扩容。 构…...

JavaScript:使用for in不是一个很好的抉择
for in 如果让你遍历对象中的key和value,你第一个想到的一定是使用for in const o{name:"chengqige",age:23 } for (let key in o){console.log(key,o[key]); }看起来是没有问题的,但是如果我在下面加一行代码,输出的结果就可能让…...
)
Go语言学习小笔记(一)
Go语言学习小笔记(一) 入口 项目的主入口:一般在main.go 包导入 一个包定义一组编译过的代码,包的名字类似命名空间,可以用来间接访问包内声明的标识符 所有处于同一个文件夹中的代码文件,必须使用同一…...
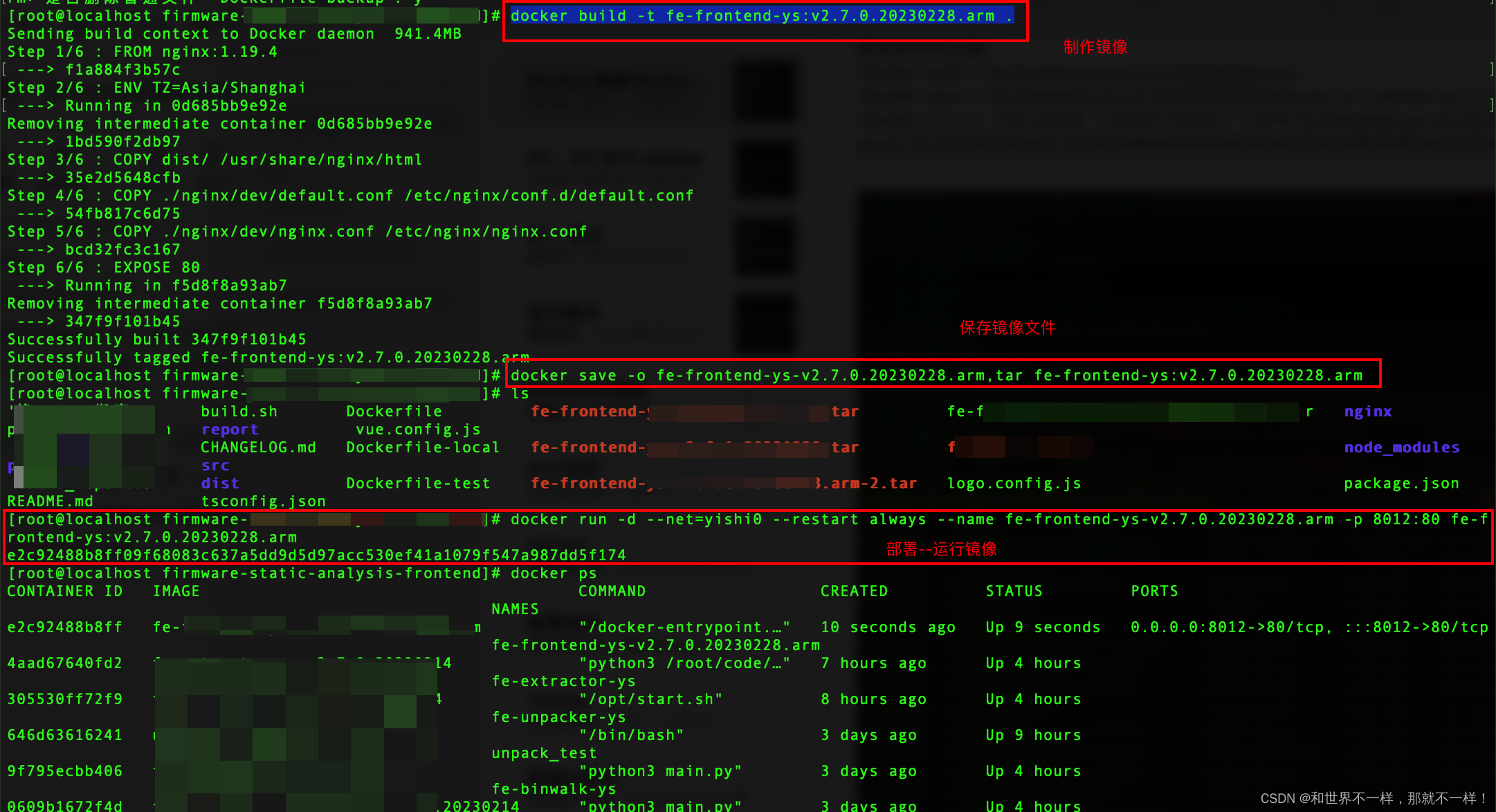
前端Docker部署方案
一、Docker容器和镜像概念 首先明确镜像和容器的概念。我们可以用 docker 构建一个镜像,这个镜像可以导入导出,用于传输,重复利用。然后如果把他 run 起来,则称为一个容器。容器是运行时,会包括运行时上下文ÿ…...

Java——无重叠区间
题目链接 leetcode在线oj题——无重叠区间 题目描述 给定一个区间的集合 intervals ,其中 intervals[i] [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。 题目示例 输入: intervals [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释…...

数据库和数据表创建与管理操作
数据库和数据表创建与管理操作 MySQL中,一个完整的而数据存储过程主要分成4步: 创建数据库确认字段创建数据表插入数据 标识符命名规则 数据库名、表名不得超过30个字符,变量名限制为29个必须只能包含 A–Z, a–z, 0–9, _共63个字符数据…...

buu [ACTF新生赛2020]crypto-rsa3 1
题目描述: from flag import FLAG from Cryptodome.Util.number import * import gmpy2 import random e65537 p getPrime(512) q int(gmpy2.next_prime) n p*q m bytes_to_long(FLAG) c pow(m,e,n) print(n) print( c ) n 177606504836499246970959030226871…...
知识库:在医疗行业的知识管理有着怎样的意义与实际影响?
知识库中还可存在一个通常被称作典型方法库的特殊部分。如果对于某些问题的解决途径是肯定和必然的,就可以把其作为一部分相当肯定的问题解决途径直接存储在典型方法库中。这种宏观的存储将构成知识库的另一部分。在使用这部分时,机器推理将只限于选用典…...

带你一步步搭建Web自动化测试框架
测试框架的设计有两种思路,一种是自底向上,从脚本逐步演变完善成框架,这种适合新手了解框架的演变过程。另一种则是自顶向下,直接设计框架结构和选取各种问题的解决方案,这种适合有较多框架事件经验的人。本章和下一张…...
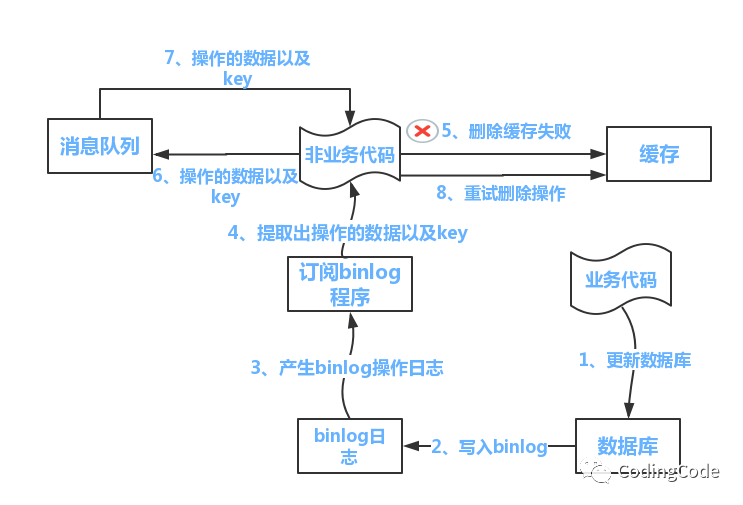
Redis进阶-缓存问题
Redis 最常用的一个场景就是作为缓存,本文主要探讨Redis作为缓存,在实践中可能会有哪些问题?比如一致性、击穿、穿透、雪崩、污染等。 为什么要理解Redis缓存问题 在高并发业务场景下,数据库大多数情况都是用户并发访问最薄弱的…...

VS Code Spring 全新功能来了!
大家好,欢迎来到我们 2023 年的第一篇博客!我们想与您分享几个与 Spring 插件、代码编辑和性能相关的激动人心的更新,让我们开始吧! Spring 插件包的新入门演练 演练(Walkthrough) 是一种多步骤、向导式的体…...

关于大数据导入流程引擎ccflow的方案
问题: 1. 现在的流程系统里有几百万条已经运行的流程其它的流程架构上 2. 需要把这样的数据导入到ccflow流程引擎里面去。 数据结构分析: 1. ccflow有流程引擎注册表,工作人表,业务数据表与日志表4大表. 2. ccflow的流程实例是一个int类型的…...

AI 生成二次元女孩,免费云端部署(仅需5分钟)
首先需要google的colab,免费版本GPU有额度。其次,打开github网站,选择一个进入colab,修改代码 !apt-get -y install -qq aria2 !pip install -q https://github.com/camenduru/stable-diffusion-webui-colab/releases/download/0.0.16/xforme…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
