字节前端实习的两道算法题,看看强度如何

最长严格递增子序列
题目描述
给你一个整数数组nums,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例:
输入:nums = [2,1,6,3,5,4]
输出:3
解释:最长递增子序列是 [1,3,4],因此长度为 3。
思路
这道题要求最长上升子序列的长度,可以使用动态规划或贪心+二分查找两种方法来解决。
-
动态规划
定义状态:dp[i]表示以第i个元素为结尾的最长上升子序列的长度。
状态转移方程:对于第i个元素,枚举其前面的元素j,如果nums[i] > nums[j],则dp[i] = dp[j] + 1。同时,在每次更新dp[i]时,更新ans为其最大值。 -
贪心+二分查找
定义一个数组d,d[i]记录长度为i的上升子序列的末尾元素的最小值。对于一个新的元素num[i],如果num[i]大于d[len],说明可以扩展当前的最长上升子序列,直接将其加入到d中;否则在d中查找第一个大于等于num[i]的元素位置pos,用num[i]替换它,使得可以扩展更长的上升子序列。
两种方法的时间复杂度分别为O(n^2)和O(nlogn),空间复杂度都是O(n)。
代码
// 方法一:动态规划:时间复杂度O(n^2) 空间复杂度O(n)
var lengthOfLIS = function(nums) {if(nums.length === 0) return 0const dp = new Array(nums.length).fill(1)let ans = 1;for(let i = 1 ; i < nums.length; i ++) {for(let j = 0 ; j < i ; j ++) {if(nums[i] > nums[j]) {dp[i] = Math.max(dp[i],dp[j] + 1);}}ans = Math.max(dp[i],ans);}console.log(dp);return ans;
}; // 方法二:贪心+二分查找:时间复杂度O(nlogn) 空间复杂度O(n)
var lenghtOfLIS = function(nums) {let n = nums.length;if(n === 0) return 0;let d = new Array(n + 1).fill(0);let len = 1;d[len] = nums[0];for(let i = 1; i < n ; i ++) {if(num[i] > d[len]) {d[++len] = nums[i];} else {let l = 1 , r = len , pos = 0;while(l <= r) {let mid = (l + r) >> 1;if(d[mid] < num[i]) {pos = mid;l = mid + 1;} else {r = mid - 1;}}d[pos + 1] = nums[i];}}return len;
}路径总和 II
题目描述
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
思路
我们可以采用深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
代码
var pathSum = function(root, target) {let ans = [],path = [];let dfs = (root,target) => {if(!root) return;path.push(root.val);target -= root.val;if(root.left === null && root.right === null && target === 0) {ans.push([...path]);}dfs(root.left,target);dfs(root.right,target);path.pop(root.val);}dfs(root,target);return ans;
};
相关文章:

字节前端实习的两道算法题,看看强度如何
最长严格递增子序列 题目描述 给你一个整数数组nums,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7…...

设计模式—策略模式
目录 一、定义 二、特点 三、优点 四、缺点 五、实例 六.涉及到的知识点 1、一个类里面有哪些东西? 2、类和实例 什么是类? 什么是实例? 什么是实例化? 3、字段和属性 什么是字段? 属性是什么࿱…...
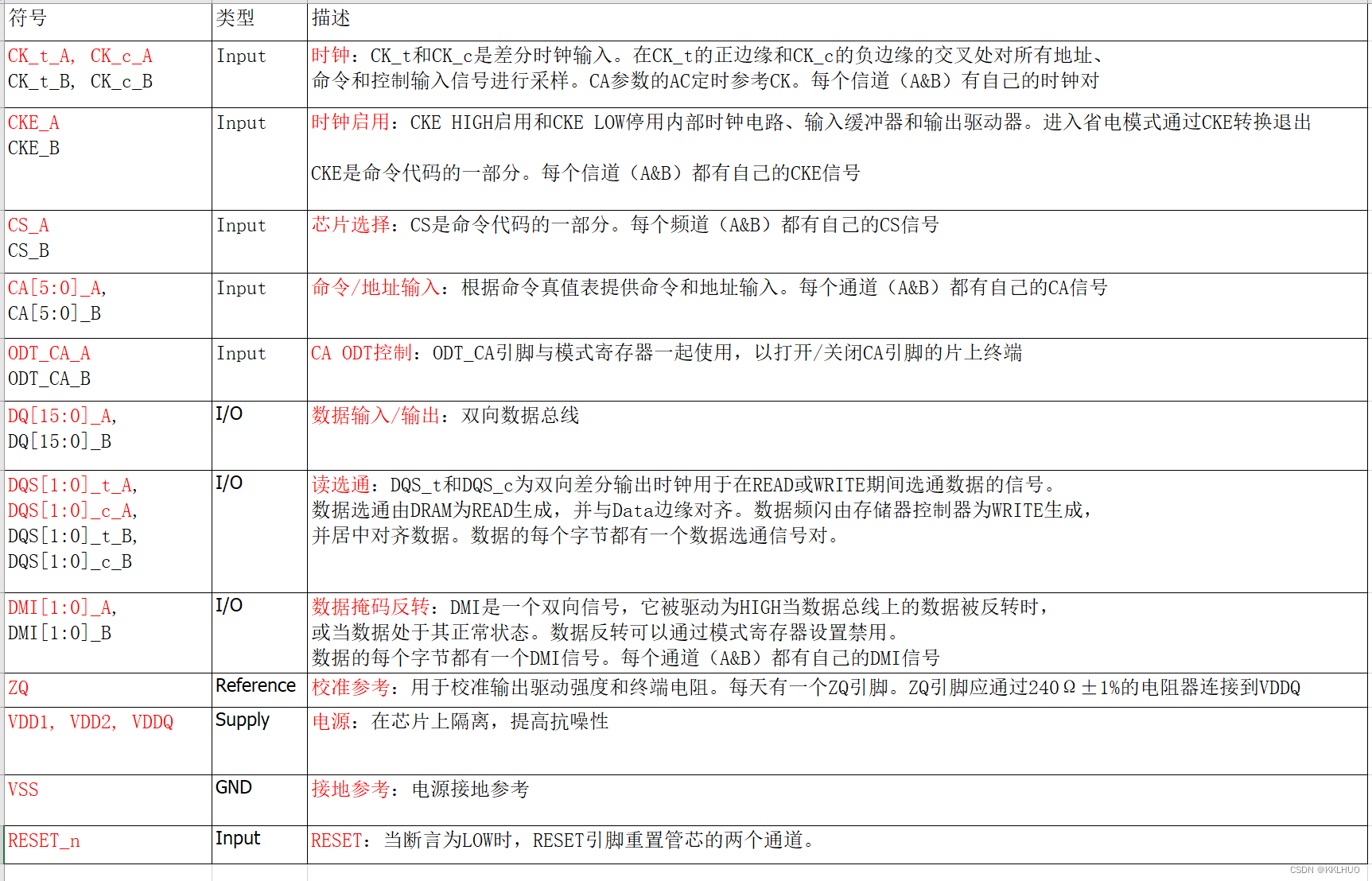
LPDDR4、DDR4
核心信息: 2400Mbps(每秒传输2400*1百万bit) 2400MT/s(百万次/秒) 信号...
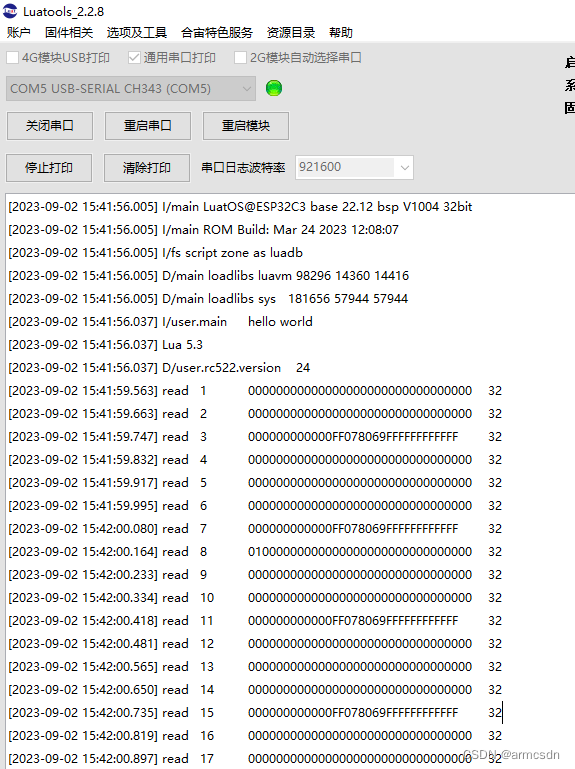
ESP32C3 LuatOS RC522①写入数据并读取M1卡
LuatOS RC522官方示例 官方示例没有针对具体开发板,现以ESP32C3开发板为例。 选用的RC522模块 ESP32C3-CORE开发板 注意ESP32C3的 SPI引脚位置,SPI的id2 示例代码 -- LuaTools需要PROJECT和VERSION这两个信息 PROJECT "helloworld" VERSIO…...
MusicBrainz Picard for Mac :音乐文件ID3编辑器
MusicBrainz Picard for Mac是一款macOS平台的音乐文件ID3编辑器,能够帮助我们在Mac电脑上编辑音乐文件的ID3标签信息,包括艺人、专辑等信息,非常快速和简单方便。Picard是下一代MusicBrainz标记应用程序。 这个新的标签概念是面向专辑的&…...

❤ Uniapp使用
❤ Uniapp使用 一、介绍 uni-app官网:https://uniapp.dcloud.io/api/media/image?idpreviewimage 微信小程序官网:https://developers.weixin.qq.com/miniprogram/dev/api/media/image/wx.previewImage.html 二、使用 1、uniapp 实现图片预览 单图预…...
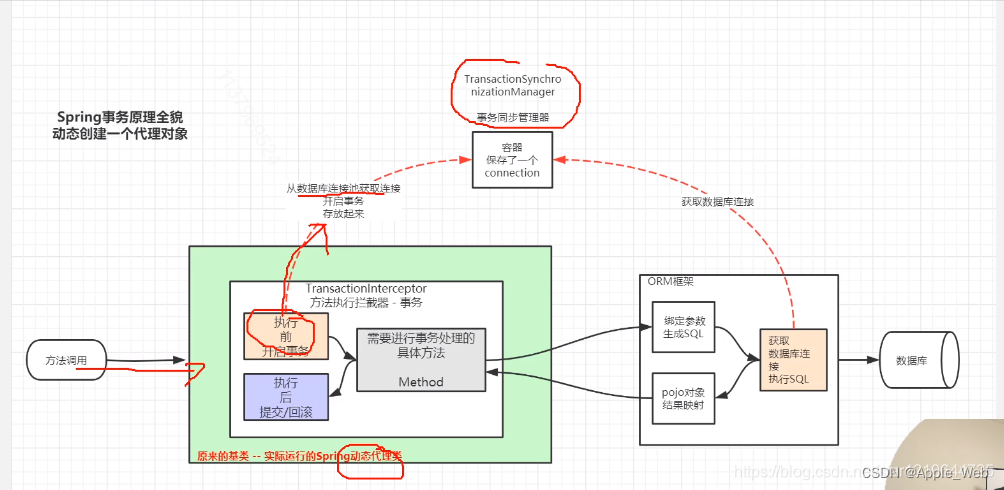
解密Spring事务生效的内部机制
声明式事务和编程式事务对比: 声明式事务: 使用注解或XML配置的方式,在代码中声明事务的属性和行为。通过AOP和代理模式实现,将事务管理与业务逻辑代码解耦。适用于大多数情况,简化了代码,提高了可维护性和…...

大数据时代下的数据安全防护
随着大数据时代的来临,数据安全防护成为了一个重要的问题。在大数据时代,数据的规模和价值都得到了极大的提升,因此数据安全的重要性也变得越来越突出。本文将从数据加密、访问控制、网络安全和人员管理四个方面来介绍大数据时代下的数据安全…...

RabbitMQ-常用命令
RabbitMQ常用命令 3.1 启动停止rabbitMQ命令 # 前台启动Erlang VM 和 RabbitMQ 当窗口关闭或者ctrlc时,使退出了。 rabbitmq-server# 使用系统命令启动 systemctl start rabbitmq-server# 后台启动 rabbitmq-server -detached# 停止rabbitMQ和Erlang VM rabbitmq-…...

Spring中依赖注入的继承bean的细节问题
介绍 有时我们会对一种类型的bean进行继承,在Spring生成bean的时候,返回类型有时是子类类型,有时会父类类型。那么到底在什么情况下用哪种类型呢?肯定有不少人会忽略这点,本篇文章就是把这个细节讲清楚 案例 父类Ba…...

海外腾讯云服务器手机上无法访问外网怎么办??
本文将介绍腾讯云服务器无法访问外网的一些常见原因以及解决办法,同时解答了手机无法访问腾讯云服务器的问题。 腾讯云服务器(Tencent Cloud Server)是一种基于云计算技术的虚拟服务器,可以满足用户对于计算、存储、网络等方面的需…...

python3+requests:接口自动化测试(二)
前言:上篇文章python3requestsunittest:接口自动化测试(一):已经介绍了基于unittest框架的实现接口自动化,但是也存在一些问题,比如最明显的测试数据和业务没有区分开,接口用例不便于…...

uni-app:允许字符间能自动换行(英文字符、数字等)
<template><view class"container"><!-- 这里是你的文本内容 -->{{ multilineText }}</view> </template><style> .container {word-break: break-all; } </style>例如: <template><view class"…...

day 42 |● 121. 买卖股票的最佳时机 ● 122.买卖股票的最佳时机II
121. 买卖股票的最佳时机 dp数组需要记录两种状态,一种是当天时手中还持有股票,一种是当天时手中已卖出股票。 func maxProfit(prices []int) int {dp : make([][]int, len(prices))dp[0] []int{-prices[0], 0}for i : 1; i < len(prices); i{val0…...
)
SQLserver基础入门理论(超基础)
♥️作者:小刘在C站 ♥️个人主页: 小刘主页 ♥️努力不一定有回报,但一定会有收获加油!一起努力,共赴美好人生! ♥️学习两年总结出的运维经验,以及思科模拟器全套网络实验教程。专栏…...
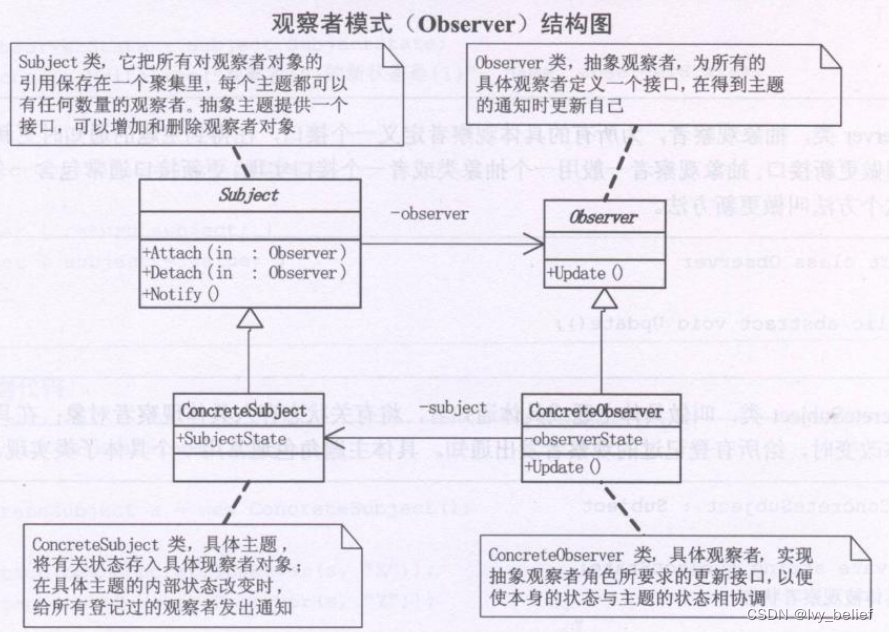
(三)行为模式:7、观察者模式(Observer Pattern)(C++示例)
目录 1、观察者模式(Observer Pattern)含义 2、观察者模式的UML图学习 3、观察者模式的应用场景 4、观察者模式的优缺点 (1)优点: (2)缺点 5、C实现观察者模式的实例 1、观察者模式&…...
2019CVPR Semantic Graph Convolutional Networks for 3D Human Pose Regression
基于语义图卷积网络的三维人体姿态回归 源码 https://github.com/garyzhao/SemGCN 摘要 在本文中,我们研究了学习图卷积网络(GCN)回归的问题。GCN的当前体系结构受限于卷积滤波器和共享的变换矩阵为的小感受野。为了解决这些限制ÿ…...
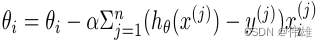
大数据课程K16——Spark的梯度下降法
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解Spark的梯度下降法; ⚪ 了解Spark的梯度下降法家族(BGD,SGD,MBGD); ⚪ 掌握Spark的MLlib实现…...
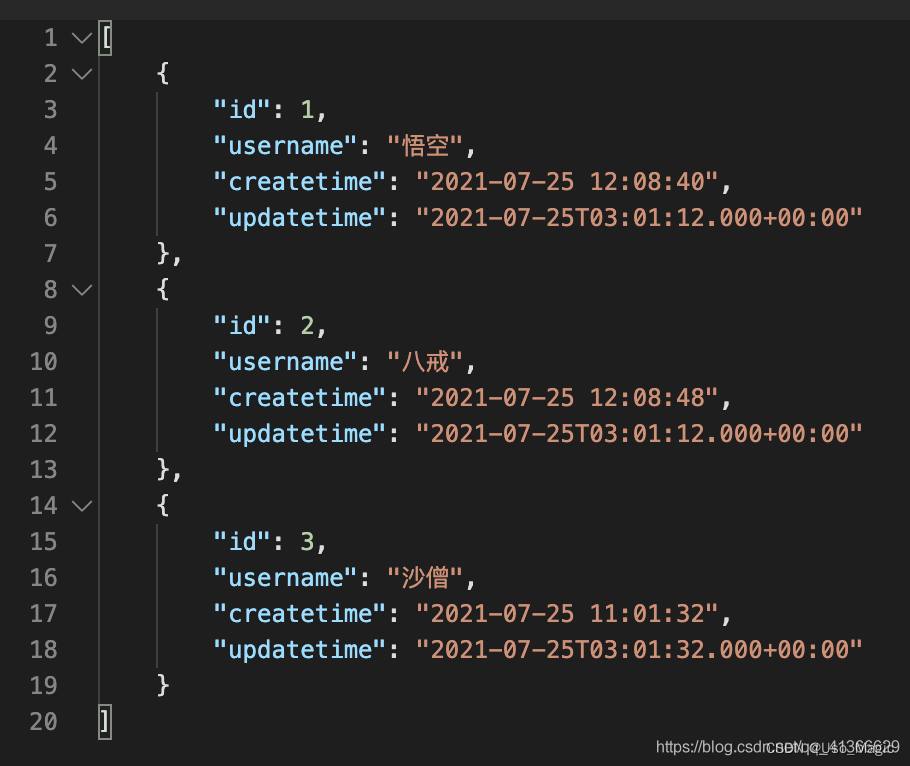
springboot:时间格式化的5种方法(解决后端传给前端的时间格式转换问题)推荐使用第4和第5种!
本文转载自:springboot:时间格式化的5种方法(解决后端传给前端的时间显示不一致)_为什么前端格式化日期了后端还要格式化_洛泞的博客-CSDN博客 时间问题演示 为了方便演示,我写了一个简单 Spring Boot 项目ÿ…...
六、vim编辑器的使用
1、编辑器 (1)编辑器就是一款软件。 (2)作用就是用来编辑文件,譬如编辑文字、编写代码。 (3)Windows中常用的编辑器,有自带的有记事本(notepad),比较好用的notepad、VSCode等。 (4)Linux中常用的编辑器,自带的最古老的vi&…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...

基于Java项目的Karate API测试
Karate 实现了可以只编写Feature 文件进行测试,但是对于熟悉Java语言的开发或是测试人员,可以通过编程方式集成 Karate 丰富的自动化和数据断言功能。 本篇快速介绍在Java Maven项目中编写和运行测试的示例。 创建Maven项目 最简单的创建项目的方式就是创建一个目录,里面…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...
