算法:分治思想处理归并递归问题
文章目录
- 算法原理
- 实现思路
- 典型例题
- 排序数组
- 数组中的逆序对
- 计算右侧小于当前元素的个数
- 总结
算法原理
利用归并思想进行分治也是很重要的一种思路,在解决逆序对的问题上有很大的需求空间
于是首先归并排序是首先的,归并排序要能写出来:
class Solution
{vector<int> tmp;
public:vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size());mergesort(nums,0,nums.size()-1);return nums;}void mergesort(vector<int>& nums,int left,int right){if(left>=right){return;}// 数组划分 [left,mid][mid+1,right]int mid=(left+right)/2;// 分块排序mergesort(nums,left,mid);mergesort(nums,mid+1,right);// 合并数组int cur1=left,cur2=mid+1,i=0;while(cur1<=mid && cur2<=right){if(nums[cur1]<=nums[cur2]){tmp[i++]=nums[cur1++];}else{tmp[i++]=nums[cur2++];}}while(cur1<=mid){tmp[i++]=nums[cur1++];}while(cur2<=right){tmp[i++]=nums[cur2++];}for(int i=left;i<=right;i++){nums[i]=tmp[i-left];}}
};
以上为归并排序基本算法原理,基于这个原理可以解决逆序对问题,逆序对问题通常问法是,给定某一个数据,在整个数组中找比这个数大或者比这个数小的数,统计这样的元素有多少个,进而返回到数组或者直接输出
那么在找寻这个过程中,这类问题的基本思路就是:左边找,右边找,左右找
在找寻的过程中需要注意的是升序和逆序问题,后续的题目中会有涉及到的地方,在这里不过总结
实现思路
大体的实现思路如上,总结下来就是划分为两个子区间,在左边找,在右边找,接着左右找,这样就能找到要求的结果
典型例题
排序数组

理解快速排序和归并排序思维的不同点
依旧是经典的排序数组问题,这次选用归并排序来解决,要了解归并排序和快速排序其实都是利用了分治的思想,把一个很复杂的问题分解为一个一个的小问题,二者在思维上有一些小小的区别,快速排序的思想是,对于某个区间来说,把这个区间进行分块,每一个分块都进行排序,每一个都进行排序,这样就完成了目的,这样的思维更像是一种前序遍历,完成了这次的任务后再向后进行延伸,而归并排序的思路和快速排序不同,归并排序的思路主要是把数组拆分成一个一个的小区间,不停的拆分,直到不能拆分后再进行组装,它的排序过程整体上而言是滞后的,更像是一种后序遍历的思想,先一直向深处找,直到找不下去了再进行排序,再一层一层向上走
class Solution
{vector<int> tmp;
public:vector<int> sortArray(vector<int>& nums) {tmp.resize(nums.size());mergesort(nums,0,nums.size()-1);return nums;}void mergesort(vector<int>& nums,int left,int right){if(left>=right){return;}// 数组划分 [left,mid][mid+1,right]int mid=(left+right)/2;// 分块排序mergesort(nums,left,mid);mergesort(nums,mid+1,right);// 合并数组int cur1=left,cur2=mid+1,i=0;while(cur1<=mid && cur2<=right){if(nums[cur1]<=nums[cur2]){tmp[i++]=nums[cur1++];}else{tmp[i++]=nums[cur2++];}}while(cur1<=mid){tmp[i++]=nums[cur1++];}while(cur2<=right){tmp[i++]=nums[cur2++];}for(int i=left;i<=right;i++){nums[i]=tmp[i-left];}}
};
数组中的逆序对

利用归并排序求逆序对是解决这类问题的常见方法,对于这个题来说,就可以采用分治的方法来解决问题
具体来说,可以把整个问题拆分为几个小步骤,把当前所在区间分成两个区间,在左边的区间内找符合逆序对的对数,再在右边的区间内找符合逆序对的对数,同时把左右两区间都进行排序,这样就可以在左右区间内都寻找符合要求的逆序对数,这就是一个轮回思路,把整个数组拆分为一个一个小区间即可解决问题,这就是分治的思想
那么思路就确认了:
- 从左边数组中找符合要求的逆序对
- 从右边数组中找符合要求的逆序对
- 从左右两边数组中找符合要求的逆序对
从排列组合的分类原理来看,这样就能找到所有的逆序对
从优化角度来讲,第三步是可以进行优化的,这就引入了要排序的原因:
如何从左右两数组中找逆序对数?
其实利用双指针的思想就可以解决,定义cur1和cur2分别指向左右两个数组,假设这里是提前排序好的,升序的数组,那么当cur1所指向的元素大于cur2所指的元素,那么cur2所指向的元素之前的元素全部满足条件,因此一次可以找出很多相同的元素,这也是这个算法的原理
因此这里就引出了为什么要进行排序,左右子区间排序后就可以通过上面的算法快速找到有多少满足要求的逆序对
处理剩余元素
-
如果是左边出现剩余,说明左边剩下的所有元素都是⽐右边元素⼤的,但是它们都是已经被计算过的,因此不会产⽣逆序对,仅需归并排序即可。
-
如果是右边出现剩余,说明右边剩下的元素都是⽐左边⼤的,不符合逆序对的定义,因此也不需要处理,仅需归并排序即可。
class Solution
{vector<int> tmp;
public: int reversePairs(vector<int>& nums) {tmp.resize(50001);return mergesort(nums,0,nums.size()-1);}int mergesort(vector<int>& nums,int left,int right){if(left>=right){return 0;}int ret=0,mid=(left+right)/2;ret+=mergesort(nums,left,mid);ret+=mergesort(nums,mid+1,right);int cur1=left,cur2=mid+1,i=0;while(cur1<=mid && cur2<=right){if(nums[cur1]<=nums[cur2]){tmp[i++]=nums[cur1++];}else{ret+=mid-cur1+1;tmp[i++]=nums[cur2++];}}while(cur1<=mid){tmp[i++]=nums[cur1++];}while(cur2<=right){tmp[i++]=nums[cur2++];}for(int i=left;i<=right;i++){nums[i]=tmp[i-left];}return ret;}
};
总体来说还是一道有思维量的hard题目,但如果掌握了分治的思想,再去下手就会容易许多
而这样的算法的时间复杂度也是很优秀的,时间复杂度是O(N)
计算右侧小于当前元素的个数

有了上面的题目的思维铺垫,解法还是比较好想的,原理就是利用归并排序进行分治的思想
但这个题和上面的问题也有区别,由于返回的是数组,因此需要记录nums中每一个数组中元素在返回数组中元素的下标,需要一一对应起来,这是比较关键的一步,也就是说,每次找到符合条件的数后,这个数应该被放到返回数组中的哪个位置?这就需要用一个辅助数组来记录原数组中每一个元素的下标所在的位置,这样就能找到了
class Solution
{vector<int> ret;vector<int> index;int tmpnums[500010];int tmpindex[500010];
public:vector<int> countSmaller(vector<int>& nums) {int n=nums.size();ret.resize(n);index.resize(n);for(int i=0;i<n;i++){index[i]=i;}mergesort(nums,0,n-1);return ret;}void mergesort(vector<int>& nums,int left,int right){if(left>=right){return;}int mid=(left+right)/2;mergesort(nums,left,mid);mergesort(nums,mid+1,right);int cur1=left,cur2=mid+1,i=0;while(cur1<=mid && cur2<=right){if(nums[cur1]<=nums[cur2]){tmpnums[i]=nums[cur2];tmpindex[i++]=index[cur2++];}else{ret[index[cur1]]+=right-cur2+1;tmpnums[i]=nums[cur1];tmpindex[i++]=index[cur1++];}}while(cur1<=mid){tmpnums[i]=nums[cur1];tmpindex[i++]=index[cur1++];}while(cur2<=right){tmpnums[i]=nums[cur2];tmpindex[i++]=index[cur2++];}for(int j=left;j<=right;j++){nums[j]=tmpnums[j-left];index[j]=tmpindex[j-left];}}
};
总结
归并递归解决分治问题主要依托于归并排序,在掌握归并的前提下找到归并过程中要找的关键信息
相关文章:

算法:分治思想处理归并递归问题
文章目录 算法原理实现思路典型例题排序数组数组中的逆序对计算右侧小于当前元素的个数 总结 算法原理 利用归并思想进行分治也是很重要的一种思路,在解决逆序对的问题上有很大的需求空间 于是首先归并排序是首先的,归并排序要能写出来: c…...

小白学Go 基础02-了解Go语言的诞生与演进
Go语言诞生于何时?它的最初设计者是谁?它为什么被命名为Go?它的设计目标是什么?它如今发展得怎么样?带着这些问题,我们一起穿越时空,回到2007年9月Go语言诞生的那一历史时刻吧。 Go语言的诞生 …...

python中如何将十进制转成二进制
python中如何将十进制转成二进制 在 Python 中,你可以使用内置的 bin() 函数将十进制数转换为二进制表示形式。以下是使用 bin() 函数进行转换的示例: decimal_number 10binary_number bin(decimal_number)print(binary_number) # 输出:…...
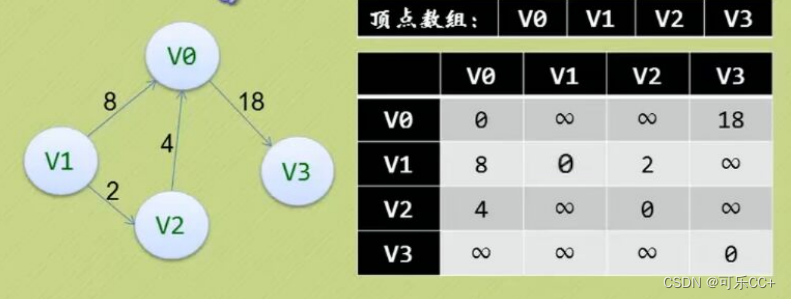
数据结构--5.0.1图的存储结构
目录 一、邻接矩阵(无向图) 二、邻接矩阵(有向图) 三、邻接矩阵(网) 四、邻接表(无向图) 五、邻接表(有向图) ——图的存储结构相比较线性表与树来说就复…...
解决win10 wsl子系统安装的ubuntu环境中lsof,netstat命令查看端口没有任何输出的问题
最近有个以前的ssm项目需要在新电脑上运行测试一下,发现需要redis环境,看了官网说:有两种选择: 1. 要么在虚拟机比如vmware安装linux基础环境,然后再安装redis 2. 要么可以利用win10的wsl linux子系统安装ubuntu&…...

【OpenFeign】OpenFeign结合Hystrix和Sentinel实现熔断降级
OpenFeign可以与Hystrix和Sentinel结合使用,实现降级和熔断。 OpenFeign与Hystrix结合使用 使用OpenFeign需要引入OpenFeign的依赖: <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-sta…...
 需求工程之需求开发与管理)
软件工程(十) 需求工程之需求开发与管理
前面我们学习到了需求工程的概念与分类,我们知道了需求工程主要分为需求开发和需求管理,但是没有说明到底该如何开发需求,有哪些方法去开发需求。到底该如何进行需求管理,又有哪些进行需求管理的方式。具体是如何去做的。下面我们将会详细进行描述。 1、需求开发 1.1、需…...
C++网狐服务器引入开源日志库spdlog
很多人对日志库不以为然,包括网狐这种十几年的公司都不重视,其实日志库记录的东西能在线上出问题时高效解决,特别是别人写的东西,人又走了,出了问题,还可以用日志分析快速解决。要是没有日志记录࿰…...

【C++】—— c++11之智能指针
前言: 本期,我们将要学习的是在c11中新提出的概念——异常指针! 目录 (一)智能指针的引入 (二)内存泄漏 1、什么是内存泄漏,内存泄漏的危害 2、内存泄漏分类(了解&a…...
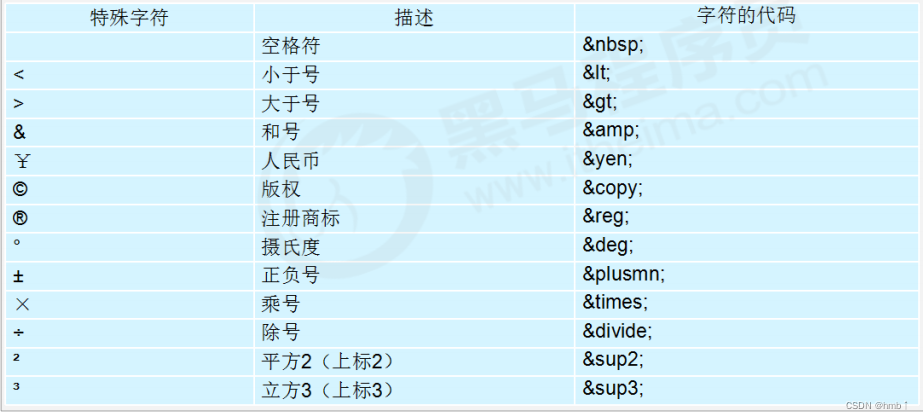
html5——前端笔记
html 一、html51.1、理解html结构1.2、h1 - h6 (标题标签)1.3、p (段落和换行标签)1.4、br 换行标签1.5、文本格式化1.6、div 和 span 标签1.7、img 图像标签1.8、a 超链接标签1.9、table表格标签1.9.1、表格标签1.9.2、表格结构标签1.9.3、合并单元格 1.10、列表1.10.1、ul无序…...

如何在 Vue TypeScript 项目使用 emits 事件
Vue是构建出色的Web应用程序的最灵活、灵活和强大的JavaScript框架之一。Vue中最重要的概念和关键特性之一是能够促进应用程序组件之间的通信。让我们深入探讨一下Vue中的“emits”概念,并了解它们如何以流畅和无缝的方式实现父子组件之间的通信。 Vue中的emits是什…...
)
文件操作 黑马教程(04)
1.文本文件 写文件 #include "iostream" #include "fstream" using namespace std; /** 文件操作** 程序运行时产生的数据都属于临时数据,程序一旦结束都会被释放* 通过文件可以将数据持久化* C中对文件操作需要包含头文件<fstream>** 文…...
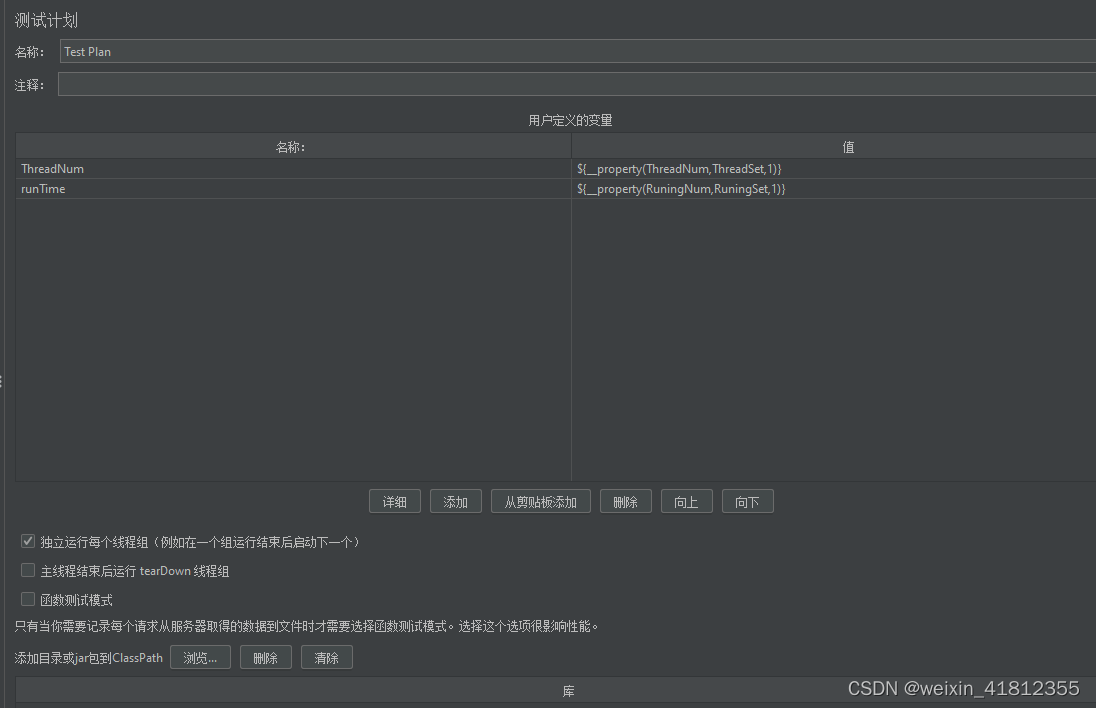
Jmeter(二十七):BeanShell PostProcessor跨线程全局变量使用
在性能测试中,两个相关联的接口不一定都在同一个线程组,遇见这种情况时,我们要进行跨线程组传参,此处用登录和查询配送单两个请求举例; 1、登录请求中配置json提取器,将接口返回的token保存在变量中&#…...
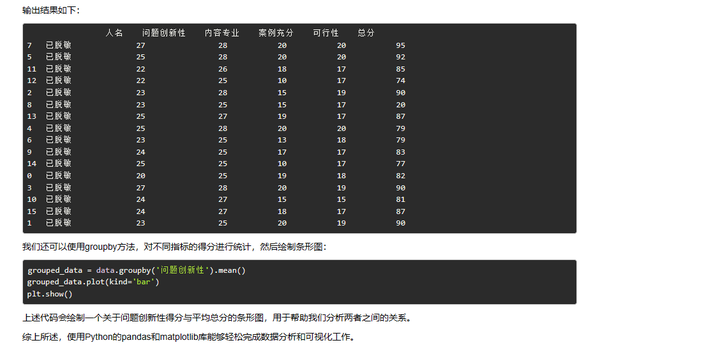
手写表格OCR识别并与大模型ChatGPT交互?
这是一张手写表格,姓名做了脱敏处理。现在需要对其识别,并分析。 直接粘贴剪切板中的表格原始图片,在网页中ctlV进行识别。识别结果列用分隔符|,可以直接粘贴到excel,进行数据列分隔。为了美观期间,也可以用…...

使用 v-for 指令和数组来实现在 Uni-app 中动态增减表单项并渲染多个数据
在 data 中定义一个数组,用于存储表单项的数据: data() {return {formItems: []} } 在模板中使用 v-for 指令渲染表单项: <template><div><div v-for"(item, index) in formItems" :key"index"><…...

xml
1.xml 1.1概述【理解】 万维网联盟(W3C) 万维网联盟(W3C)创建于1994年,又称W3C理事会。1994年10月在麻省理工学院计算机科学实验室成立。 建立者: Tim Berners-Lee (蒂姆伯纳斯李)。 是Web技术领域最具权威和影响力的国际中立性技术标准机构。 到目前为…...

Java中的动态代理(JDK Proxy VS CGLib)
前言 动态代理可以说是Java基础中一个比较重要的内容,这块内容关系到Spring框架中的AOP实现原理,所以特别写了一篇作为个人对这块知识的总结。这部分内容主要包括:JDK Proxy和CGLib的基本介绍、二者的实现原理、代码示例等。 什么是动态代理…...
)
Redis 7 第七讲 哨兵模式(sentinal)
哨兵模式 哨兵巡查监控后台master主机是否故障,如果出现故障根据投票时自动将某一个从库转换成新的主库,继续对外服务。 作用 1. 监控redis运行状态,包括master和slave 2. 当master down机,能自动将salve切换成新的master 应用场景 主从监控监控主从redis库运行的状态…...

Python入门教程 - 判断语句(二)
目录 一、布尔类型 二、比较运算符 三、if判断语句 一、布尔类型 True False result1 10 > 5 result2 10 < 5 print(result1) print(result2) print(type(result1)) True False <class bool> 二、比较运算符 ! > < > < 比较运算的结果是布尔…...

LeetCode-55-跳跃游戏-贪心
题目描述: 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 解…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...
