leetcode - 360周赛
一,2833. 距离原点最远的点

这道题的意思是,遇到 "L" 向左走,遇到 "R" 向右走,遇到 "_" 左右都可以走,那么要想找到距离原点最远的点,就是在找 | "L" + "R" | + "_"
代码如下:
class Solution {public int furthestDistanceFromOrigin(String moves) {int _cnt = 0, L = 0, R = 0;for(int i=0; i<moves.length(); i++){if(moves.charAt(i) == '_'){_cnt++;}else if(moves.charAt(i) == 'L'){L++;}else{R++;}}return Math.abs(L-R)+_cnt;}
}二,2834. 找出美丽数组的最小和

这道题要我们求最小和,那么我们肯定是从1开始往后遍历,而且题目要求不存在两个不同的下标 i 和 j,使得 nums[i] + nums[j] == target,说明 当 nums[i] + nums[j] == target 时,我们只能在其中选择较小的值,例如 :3 + 5 == 8,我们要求最小和,那么就只能选择 3 。还有一种情况,当我们遍历到的正整数 >= target 时,就不会存在上面两数相加等于target的情况,可以直接加入。
代码如下:
class Solution {public long minimumPossibleSum(int n, int target) {long sum = 0;int i = 1;int k = 0;while(k < n){// i 是 nums[i], target-i 是 nums[j]if(i <= target-i){sum += i; k++;}if(i >= target){sum += i;k++;}i++;}return sum;}
}三,2835. 使子序列的和等于目标的最少操作次数

题目告诉我们nums中存的是2的幂,所以关键是要想到使用二进制来拼凑出 target 的每一个二进制位中的 1。
1. 当 sum < target 时,因为每一个2^i 都能分成 2^i 个 1,所以我们只能得到[0,sum]中的数,说明不可能得到 target ,直接 return -1.
2. 当 sum >= target 时,求最少的操作次数,最好的情况是,nums中有一个数 或 小于target的几个数的和 恰好等于 target, 这样看来,要求最小的操作次数,我们就要从二进制的低位向高位去考虑,因为我们要先考虑能不能直接用小于target的数凑出target。
3. target 的第 i 个二进制位的获取方法:
- 如果 nums 中 <= 2^i 的值的和 >= 2^i ,那么一定可以直接凑出 2^i ,直接continue
- 如果和小于 2^i,那么我们只能在nums中找到大于2^i 的值 2^j (j > i),然后通过不断的 /2 来得到 2^i,又因为 /2 的值都会重新放入数组 nums 中,所以 target 中第 i 到 第 j-1 的二进制位都不需要再算了,直接从第 j 个二进制位开始。
证明1,(s表示<=2^i的数字之和):
- 当 i = 1,s >= 2^1 时,
1)nums中存在2,很明显结论正确。
2) nums中不存在2,那么nums中 < 2^1 的数是 1,而 1 + 1 也能得到2,结论成立。
- 当 i = 2, s >= 2^2 时,
1)nums中存在4,很明显结论正确。
2)nums中不能在4,那么nums中 < 2^2 的数有 1/2,即<=2^1,s >= 2^2 >= 2^1,根据上面得出的结论,可以得到一个2,那么剩下的 s-2 >= 2,同理,也成立。
- 当 i = 3,s >= 2^3 时,
1)nums中存在8,很明显结论正确。
2)nums中不存在8,那么nums中 < 2^3 的数是 1/2/4,即<=2^2,s >= 2^3 >= 2^2,根据上面的结论,可以得到一个4,那么剩下的 s-4 >= 4,同理,也成立。
由此类推,我们就可以得出结论:如果 nums 中 <= 2^i 的值的和 >= 2^i ,那么一定可以直接凑出 2^i
代码如下:
class Solution {public int minOperations(List<Integer> nums, int target) {long sum = 0;//31是根据数据范围确定,从前往后依次代表的是2^0 2^1....int[] cnt = new int[31];for(int x : nums){sum += x;for(int i=0; i<31; i++){//类似于哈希,记录nums数组中2^i有几个cnt[i] += x >> i & 1;}}if(sum < target) return -1;int i = 0, ans = 0, s = 0;while(1L<<i <= target){s += cnt[i]*(1<<i);// <=2^i的数的和int mask = (1<<(i+1))-1;//j=ii += 1;if(s >= (target&mask)){// target&mask 是得到target的0~i位的二进制数continue;}ans += 1;//当前2^j在nums中不能通过累加或直接得到while(cnt[i] == 0){//在nums中找到大于2^j的数,然后一路分割ans += 1;i += 1;}}return ans;}
}四,2836. 在传球游戏中最大化函数值
 这道题可以暴力枚举,但是因为数据范围太大,所以需要优化,这里使用了树上倍增的算法思想,直接看代码:
这道题可以暴力枚举,但是因为数据范围太大,所以需要优化,这里使用了树上倍增的算法思想,直接看代码:
class Solution {/**dp[i][j]: 从j开始,走2^i所能到达的位置sum[i][j]: 从j开始,走2^i所能得到的和*/public long getMaxFunctionValue(List<Integer> receiver, long K) {int n = receiver.size();int m = 64 - Long.numberOfLeadingZeros(K); //K的二进制长度int[][] dp = new int[m][n];long[][] sum = new long[m][n];for (int i = 0; i < n; i++) {//初始化dp[0][i] = receiver.get(i);sum[0][i] = receiver.get(i);}for (int i = 0; i < m - 1; i++) {for (int x = 0; x < n; x++) {dp[i+1][x] = dp[i][dp[i][x]];sum[i+1][x] = sum[i][x] + sum[i][dp[i][x]];//合并节点值之和}}long ans = 0;for (int i = 0; i < n; i++) {long s = i;int x = i;for (long k = K; k > 0; k &= k-1) {int ctz = Long.numberOfTrailingZeros(k);//从低到高最后一个0的位置相当于要走2^ctzs += sum[ctz][x];x = dp[ctz][x];}ans = Math.max(ans, s);}return ans;}
}
相关文章:

leetcode - 360周赛
一,2833. 距离原点最远的点 这道题的意思是,遇到 "L" 向左走,遇到 "R" 向右走,遇到 "_" 左右都可以走,那么要想找到距离原点最远的点,就是在找 | "L" "R&qu…...

Android 1.1 背景相关与系统架构分析
目录 1.1 背景相关与系统架构分析 分类 Android 基础入门教程 1.Android背景与当前的状况 2.Android系统特性与平台架构 系统特性: 平台架构图: 架构的简单理解: 3.本节小结: 1.1 背景相关与系统架构分析 分类 Android 基础…...
系统架构技能之设计模式-抽象工厂模式
一、上篇回顾 上篇我们主要讲述了简单工厂模式和工厂模式。并且分析了每种模式的应用场景和一些优缺点,我们现在来回顾一下: 简单工厂模式:一个工厂负责所有类型对象的创建,不支持无缝的新增新的类型对象的创建。 工厂模式&…...

clangd的使用,实现跳转提示
一、插件卸载c插件下载clangd 二、设置搜索clangd --compile-commands-dirbuild文件中compile_commands的绝对路径若没有找到compile_commands.json文件可以通过如下方式之后再便于即可生成 cmake项目: 在项目最顶层的.cmake文件中或者CMakeList文件中加入如下命令…...

2023应届生java面试搞笑之一:CAS口误说成开心锁-笑坏面试官
源于:XX网,如果冒犯,表示歉意 面试官:什么是CAS 我:这个简单,开心锁 面试官:WTF? 我:一脸自信,对,就是这个 面试官:哈哈大笑ÿ…...

nginx-concat
为了减少tcp请求数量,nginx从上有服务器获取多个静态资源(css,js)的时候,将多个静态资源合并成一个返回给客户端。 这种前面有两个问号的请求都是用了cancat合并功能。 先到官网下载安装包,拷贝到服务器编译…...
Java 大厂面试 —— 常见集合篇 List HashMap 红黑树
23Java面试专题 八股文面试全套真题(含大厂高频面试真题)多线程_软工菜鸡的博客-CSDN博客 常见集合篇-01-集合面试题-课程介绍 02-算法复杂度分析 2 List相关面试题 2.1 数组 2.1.1 数组概述 数组(Array)是一种用连续的内存空…...

剪枝基础与实战(5): 剪枝代码详解
对模型进行剪枝,我们只对有参数的层进行剪枝,我们基于BatchNorm2d对通道重要度 γ \gamma γ参数进行稀释训练。对BatchNorm2d及它的前后层也需要进行剪枝。主要针对有参数的层:Conv2d、BatchNorm2d、Linear。但是我们不会对Pool2d 层进行剪枝,因为Pool2d只用来做下采样,没…...
)
Acwing 897. 最长公共子序列 (每日一题)
最长公共子序列 题目描述 给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。 输入格式 第一行包含两个整数 N和 M。 第二行包含一个长度为 N 的字符串,表示字符串 A。 第三行包含一个长度为 M …...
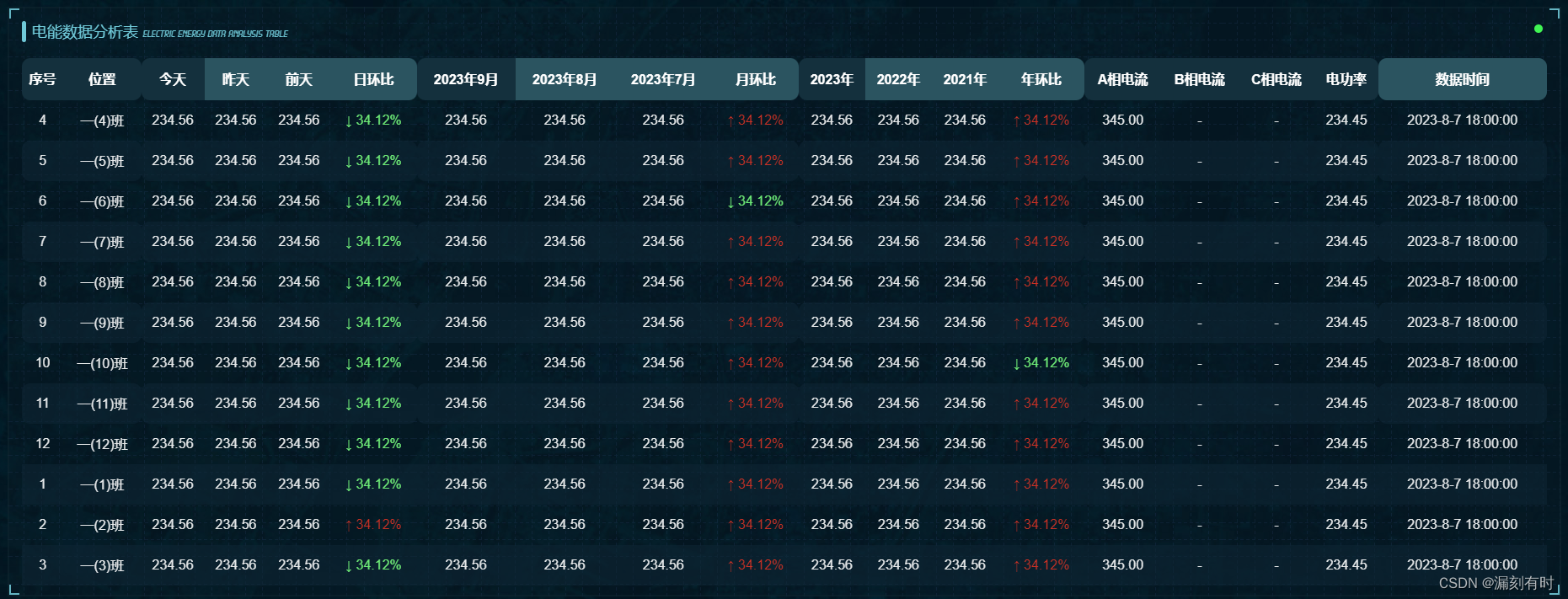
CSS中border-radius的来美化table的实战方案
border-radius是一种CSS属性,用于设置元素的边框的圆角程度。其具体的用法如下: 设置一个值:可以为元素设置一个单一的圆角半径,这个半径将应用于元素的四个角。例如: div {border-radius: 10px; }设置四个值&#x…...
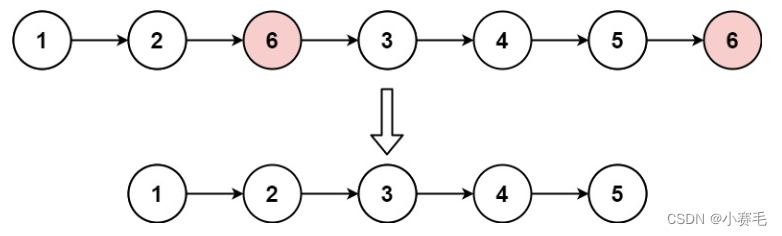
移除链表元素_每日一题
“路虽远,行则将至” ❤️主页:小赛毛 ☕今日份刷题:移除链表元素 题目描述: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例1&…...
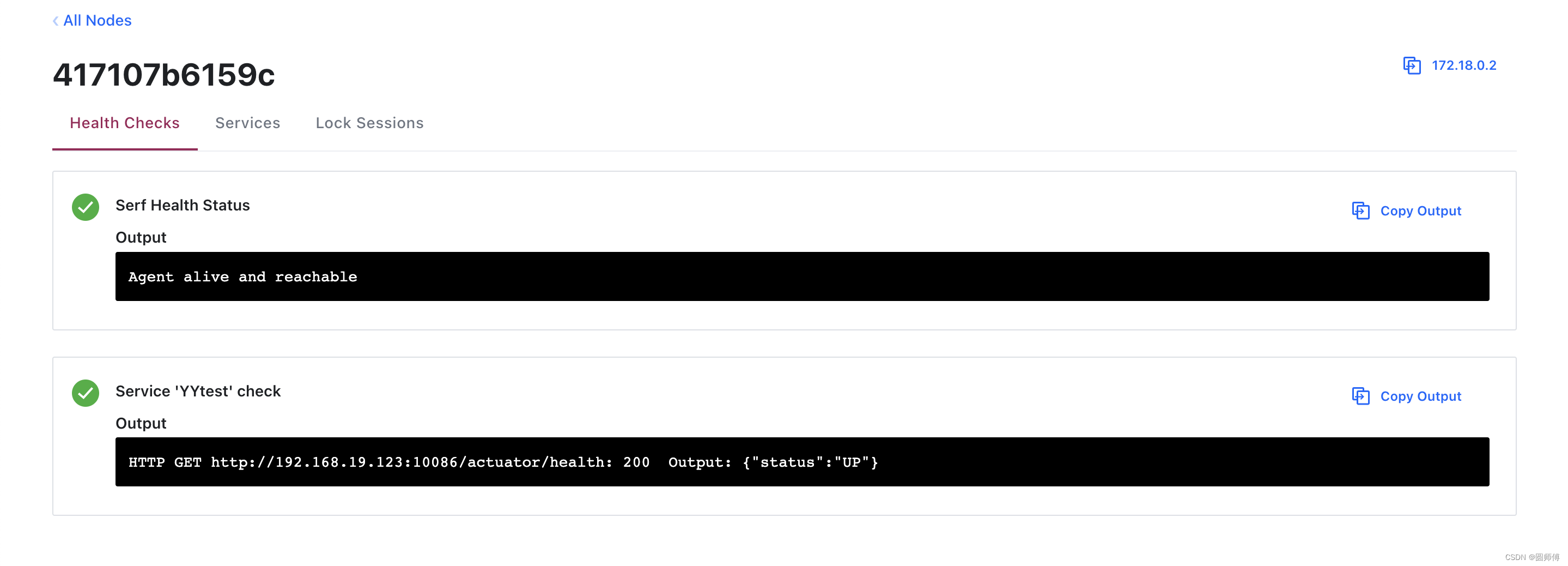
spring boot + Consul 示例 (Kotlin版)
文章目录 1.docker 安装consul2.创建基于springboot的client2.1 依赖版本2.2 pom.xml2.3 启动类2.4 application.properties 3 搭建完成4. 总结 1.docker 安装consul docker-compose.yaml version: "3"services:consul:image: consul:1.4.4container_name: consule…...

Git企业开发控制理论和实操-从入门到深入(四)|Git的远程操作|Gitee
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...
SpringCloudAlibaba Gateway(二)详解-内置Predicate、Filter及自定义Predicate、Filter
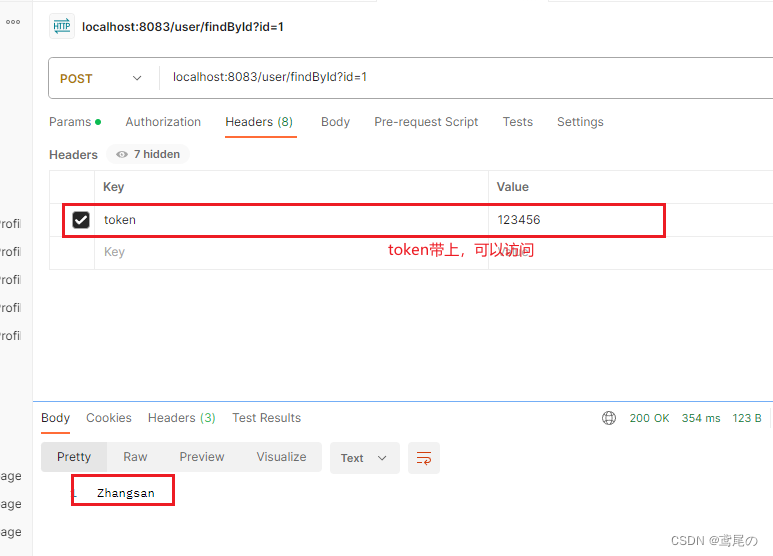
Predicate(断言) Predicate(断言),用于进行判断,如果返回为真,才会路由到具体服务。SpirnngCloudGateway由路由断言工厂实现,直接配置即生效,当然也支持自定义路由断言工厂。 内置路由断言工厂实现 SpringClo…...

调用chat-gpt
调用chat-gpt 依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</groupId><artifact…...

Element组件浅尝辄止6:Dialog 对话框组件
Dialog 对话框组件:在保留当前页面状态的情况下,告知用户并承载相关操作。 大白话就是弹窗组件,日常开发中比较常见 1.怎样使用? //触发方式 <el-button type"text" click"dialogVisible true">打开&…...

Bert和LSTM:情绪分类中的表现
一、说明 这篇文章的目的是评估和比较 2 种深度学习算法(BERT 和 LSTM)在情感分析中进行二元分类的性能。评估将侧重于两个关键指标:准确性(衡量整体分类性能)和训练时间(评估每种算法的效率)。…...

【面试经典150题】跳跃游戏
题目链接 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 1 < nums…...

【Rust】003-基础语法:流程控制
【Rust】003-基础语法:流程控制 文章目录 【Rust】003-基础语法:流程控制一、概述二、if 表达式1、语法格式2、多个3、获取表达式的值 三、循环1、loop:无限循环,可跳出无限循环跳出循环返回值 2、while:条件循环&…...
0829【综述】面向时空数据的区块链研究综述
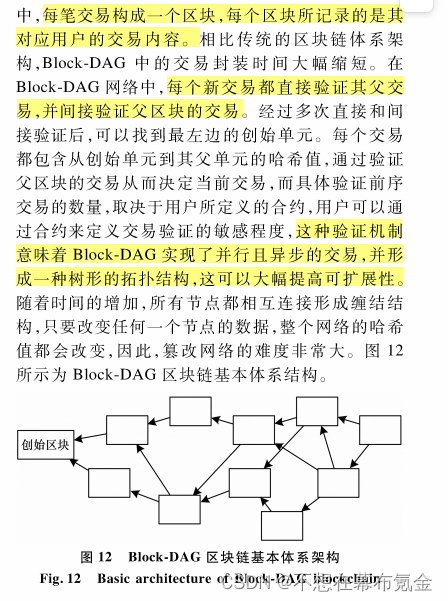
摘要:时空数据包括时间和空间2个维度,常被应用于物流、供应链等领域。传统的集中式存储方式虽然具有一定的便捷性,但不能充分满足时空数据存储及查询等要求,而区块链技术采用去中心化的分布式存储机制,并通过共识协议来保证数据的安全性。研究现有区块链1.0、2.0和以Block-DAG为…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
